Main

The properties of metal nanoclusters can deviate substantially from bulk metals owing to quantum confinement effects1. While bulk metals are described by band theory, nanoclusters with free-electron metals can be described by the jellium model, where valence electrons in the nanocluster are subject to a uniform potential2,3,4,5. The jellium model emphasizes closed-shell electron configurations 1S21P61D102S21F142P61G182D10… with electron magic numbers 2, 8, 18, 20, 34, 40, 58, 68… but an open-shell variation with magic numbers 1, 5, 13, 19, 27, 37, 49, 63… and jellium aromaticity has been proposed6. Such clusters have been termed superatoms because collectively they behave like an atom, extending the periodic table into a ‘third dimension’1,5. Superatoms have demonstrated altered properties, such as increased electron affinity, that is, superhalogens7,8, and anomalous magnetic susceptibilities9, and since they offer atom-level modifications to engineer superatom properties, they promise numerous opportunities in catalysis, materials and devices10,11.

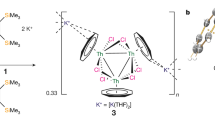
Superatom clusters inherently feature metal–metal bonding, which requires sufficiently diffuse metal valence orbitals. Thus, for the decades that superatoms have been known, they have been based on main group or transition metals1,2,3,4,5,7,8,9,10,11. By contrast, although f elements, and in particular actinides, have been considered computationally as dopants into superatoms12,13,14, the relatively limited radial distribution of actinide 5f valence orbitals has restricted the number of compounds featuring actinide–actinide bonding15,16,17,18,19,20,21,22. Notably, endohedral fullerene-encapsulated Th2, U2 and Th2F have been prepared19,20,22, but those actinide–actinide bonds cannot be readily translated to synthetic molecular chemistry. Previously, we discovered that reduction of the thorium complex [Th(η8-C8H8)(Cl)2(THF)2] (1)23 by the cyclobutadienyl reagent [K2{C4(SiMe3)4}] (2)24 produced the diamagnetic two-electron trithorium nanocluster [{Th(η8-C8H8)(μ3-Cl)2}3{K(THF)2}2]∞ (3)21, which features three-centre-two-electron Th 6d-based metal–metal bonding. Conspicuously, while one-electron U–U and Th–Th bonds have been proposed in endohedral fullerenes19,22, experimental spectroscopic and magnetic verification has been lacking. Experimental isolation and confirmation of one-electron actinide–actinide bonding beyond trapped dimetal units would thus be anticipated to afford unusual properties. The isolation of 3 suggested to us that one-electron mixed-valence actinide–actinide nanocluster bonding might be accessible utilizing the 6d-orbitals of thorium.

In this Article, we report the preparation and isolation of the crystalline mixed-valence trithorium nanoclusters [M(2.2.2-cryptand)][{(η8-C8H8)Th(μ-Cl)2}3] (4M, M = K, 4K; Rb, 4Rb; Cs, 4Cs) that exhibit three-centre-one-electron actinide–actinide bonding. Experimental and computational analysis demonstrates Robin–Day Class III formalism 6d-orbital valence delocalization in these clusters. These clusters are paramagnetic, which should be the dominant physicochemical behaviour, but in external applied magnetic fields, they instead exhibit exalted diamagnetic responses, experimentally evidencing actinide superatom and open-shell jellium aromaticity.

Results and discussion

Synthesis

Previously, we reported that reduction of the thorium complex [Th(η8-C8H8)(Cl)2(THF)2] (1)23 by the cyclobutadienyl reagent [K2{C4(SiMe3)4}] (2)24 produced the diamagnetic two-electron reduced trithorium nanocluster [{Th(η8-C8H8)(μ3-Cl)2}3{K(THF)2}2]∞ (3)21, which features three-centre-two-electron Th 6d-based metal–metal bonding (Fig. 1). In our report of 3, its high-yield isolation (89%) resulted from rapid formation and precipitation enabled by the strongly reducing and soluble nature of 2. Indeed, reduction of 1 to give 3 using the heterogeneous reductant KC8 was low yielding (10%). Targeting one-electron reduction, we modulated the slow reaction of 1 with MC8 (M = K, Rb, Cs) by addition of 2.2.2-cryptand to increase efficacy without over-reduction. Hence, careful addition of a 1:1 solution of 1 and 2.2.2-cryptand in THF to one equivalent of MC8 (M = K, Rb, Cs) in benzene produces, after work-up, analytically pure blue [M(2.2.2-cryptand)][{(η8-C8H8)Th(μ-Cl)2}3] (4M, M = K, 4K; Rb, 4Rb; Cs, 4Cs) 4M in 10–39% isolated crystalline yields (Fig. 1). Once formed, 4M are insoluble in hydrocarbon and arene solvents, soluble with limited stability in deuterated tetrahydrofuran, and soluble and stable for several hours in 1,2-dimethoxyethane. Compounds 4M are thermally sensitive; powdered samples are stable for weeks when stored cold, but when stored at room temperature, they slowly decompose over days, evidenced by the blue colour fading to colourless, while in solution they decompose immediately at temperatures above 35 °C. Compounds of 4M also readily precipitate from cold tetrahydrofuran and 1,2-dimethoxyethane solutions, limiting the use of variable-temperature NMR studies (Supplementary Figs. 37–44). However, freshly prepared and recrystallized samples of 4M were amenable to analysis in the solid state and also when dissolved (solution or frozen) in 1,2-dimethoxyethane (see later).

Fig. 1: Synthesis of 3 and 4M (M = K, Rb and Cs).
figure 1

In previous work (ref. 21), treatment of 1 with 2 afforded 3, which contains a three-centre-two-electron trithorium bonding interaction. In this work, treatment of 1 and 2.2.2-cryptand with MC8 reducing agents affords complexes 4M (M = K, Rb, Cs). The fate of the excess M and 2.2.2-cryptand component was not determined.

Full size image

Solid-state structures

The solid-state structures of 4M were determined by single-crystal X-ray diffraction (Fig. 2, Supplementary Figs. 1–3 and Supplementary Table 1). Complexes 4M were also examined by powder X-ray diffraction, but, despite affording satisfactory elemental analyses, unfortunately, the highly air-sensitive nature of these complexes precluded definitive confirmation of phase purities (Supplementary Figs. 5–7 and Supplementary Table 2). The structures of 4M reveal separated ion pairs with [M(2.2.2-cryptand)]+ cation and [{(η8-C8H8)Th(μ-Cl)2}3]− anion components. Each thorium adopts a four-legged piano-stool geometry, being η8-coordinated to a cyclooctatetraenyl ligand and bonded to four bridging chlorides. The three Th–Th distances in 4Cs (Fig. 2) span the range 4.0463(2)–4.0811(2) Å ((average) av. 4.0689(3) Å), similar to those of 4K (4.0578(11)–4.0899(11) Å, av. 4.0713(13) Å) and 4Rb (4.0480(5)–4.0860(5) Å, av. 4.0717(9) Å). This is longer than the sum of the covalent single-bond radii of two thorium atoms of 3.5 Å (ref. 25), but well within the corresponding van der Waals distance of 4.74 Å, and longer than the Th–Th distances in 3 (3.9896(4)–3.9947(5) Å, av. 3.991(2) Å)21 and endohedral fullerene Th2 (3.816(6) Å)20 and Th2F (3.651(3) Å)22. Focusing on 4Cs, while noting that 4M are all similar, the cyclooctatetraenyl C–C distances are unremarkable (av. C–C distance of 1.40(2) Å) and, by the 3σ criterion, the average Th–C value in 4Cs (2.719(16) Å) is not statistically different to the average Th–C distances in 3 (2.738(20) Å), 1 (2.734(2) Å) and thorium(III)- and thorium(IV)-cyclooctatetraenyl complexes23,26,27. The Th–Cl distances in 4Cs (av. 2.8459(15) Å) are unexceptional, and the Th–Cl–Th angles span a narrow range 90.63(3)–91.70(3)°, where in each Th(μ-Cl)2Th unit, the Cl···Cl distances average 3.484(15) Å, suggesting the absence of any Cl···Cl interactions. The crystallographic data suggest that the sub-valent nature of the thorium ions in 4M is of 6d rather than 5f character, since populating d orbitals typically produces small (<0.10 Å) changes to metal–ligand distances, whereas f-orbital population typically produces ≥0.10 Å changes.

Fig. 2: Single-crystal solid-state structure of 4Cs.
figure 2

Single-crystal X-ray diffraction solid-state structure of 4Cs determined at 150 K. Displacement ellipsoids are rendered at 40% probability and hydrogen atoms are omitted for clarity. The structures of 4K and 4Rb are analogous (Supplementary Figs. 1 and 2), but with the Cs+ cation replaced by K+ or Rb+ cations, respectively. Key: thorium, green; chlorine, magenta; cesium, purple; oxygen, red; carbon, grey; nitrogen, blue.

Full size image

Electronic structure calculations

To understand the electronic structure of the trithorium components of 4M and rationalize the characterization data, we carried out quantum chemical calculations on the [{(η8-C8H8)Th(μ-Cl)2}3]– anion component of 4M (4′) in its doublet ground state (Supplementary Tables 13 and 14). A domain-based local-pair natural orbital coupled cluster calculation yielded a T1 diagnostic value of ~0.0087, far below the threshold above which multi-configurational effects are considered relevant (~0.05 for open-shell systems). Hence, 4′ has predominant single-reference character, and density functional theory (DFT) is thus an appropriate method with which to probe its electronic structure. PBE0 all-electron SARC geometry optimized 4′ has no imaginary frequencies, and exhibits average Th–Th distances of 4.09 Å, close to the experimental average (4.07 Å). The computed properties of 4′ reproduce the experimental magnetic, Raman, ultraviolet/visible/near infrared (UV/vis/NIR) and electron paramagnetic resonance (EPR) spectroscopic data (see later), providing experimental verification of the electronic structure of 4′. Furthermore, an energy decomposition analysis of 4Cs (Supplementary Fig. 123 and Supplementary Table 16) reveals, as expected, that the interaction energy of the [{(η8-C8H8)Th(μ-Cl)2}3]− and [Cs(2.2.2-cryptand)]+ fragments is dominated by electrostatic interactions, which constitute 72% of the total attractive energy contributions (Supplementary Text).

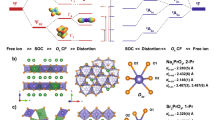
The DFT α-spin highest occupied molecular orbital (HOMO) of 4′ is a three-centre-one-electron valence-delocalized singly occupied molecular orbital (SOMO; Fig. 3a), which resembles the doubly occupied HOMO of [{Th(η8-C8H8)(μ3-Cl)2}3(K)2] (3′) (Fig. 3b)21. Mulliken population analysis of the SOMO of 4′ reveals it to be of 86% Th and 9% Cl character. The Th component is 62/14/7% 6d/5f/7p character, which is similar to the corresponding HOMO of 3′.

Fig. 3: Comparison of DFT molecular orbital and quantum theory of atoms-in-molecules molecular graphs of 4′ and 3′.
figure 3

a, The highest, singly occupied molecular orbital of the [{(η8-C8H8)Th(μ-Cl)2}3]– anion component of 4M (4′). b, The highest, doubly occupied molecular orbital of the model [{Th(η8-C8H8)(μ3-Cl)2}3(K)2] of 3 (3′), with potassium cations omitted for clarity. c, Molecular graph of 4′. d, Molecular graph of 3′. The molecular orbitals are plotted at the 0.05 isosurface level, and the molecular graphs are plotted with critical point electron density thresholds of 0.01 a.u. showing bond paths (black lines) and bond critical points (blue dots). Key: thorium, green; chlorine, magenta; carbon, grey; hydrogen, white.

Full size image

The quantum theory of atoms-in-molecules (QTAIM) analysis of 4′ (Fig. 3c) finds Th–Th bond paths that are less curved than in 3′ (Fig. 3d). The bond path curvature reflects the accumulation of electron density in the centre of the trithorium triangle and hence the number of electrons in the SOMO of 4′ and HOMO of 3′. The bond critical point (BCP) properties also reflect the differences between 4′ and 3′. For 4′, the electron density (ρ) at the Th–Th BCPs is 0.014 a.u. and the Laplacian (\({{\nabla }^{2}\rho }_{{\rm{BCP}}}\)) is –7 × 10–3 a.u. (0.022 a.u. and –9 × 10–3 a.u. in 3′, respectively). The small value of \({{\nabla }^{2}\rho }_{{\rm{BCP}}}\) indicates a flat electron density distribution. Reduced Th–Th bonding in 4′ is also reflected in the QTAIM delocalization index, which is 0.12 (0.26 in 3′) and the Th–Th Mayer bond order (MBO) of 0.27 (0.45 in 3′). The QTAIM and MBO data consistently find Th–Th bond properties in one-electron 4′ that are approximately half those of two-electron 3′, and this bonding picture is reinforced by adaptive natural density partitioning, electron density of delocalized bonds, multicentre indices, electron localization function, iso-chemical shielding surface, and Foster–Boys and Pipek–Mezey localization schemes (Supplementary Materials and Methods and Supplementary Figs. 115, 116, 119 and 120).

Spectroscopic characterization

The Raman spectra of 4M (Fig. 4a, Supplementary Figs. 67–81 and Supplementary Table 3) exhibit inelastic scattering bands at ~53 cm−1, ~75 cm−1, ~99 cm−1 and ~135 cm−1 that involve the trithorium cores and correspond, using D3h symmetry labels, to two doubly degenerate bending modes (\({E}^{{\prime} }\)), a symmetric breathing mode (\({{\rm{A}}}_{1}^{{\prime} }\)) and an antisymmetric breathing mode (\({{\rm{A}}}_{1}^{{\prime} {\prime} }\), Cl atoms moving the opposite direction to the rest of the molecule). For 4′, the corresponding calculated frequencies of 51.4/51.5 cm–1, 67.3/67.5 cm–1, 88.7 cm–1 and 136.0 cm–1 (Supplementary Fig. 117) compare well with the experimental values (Fig. 4a).

Fig. 4: Spectroscopic and magnetic data for 4Cs and 5.
figure 4

a, Selected portion of the Raman spectrum (black line) of 4Cs with DFT computed inelastic scattering bands (red sticks). b, UV/vis/NIR spectrum (black line) of 4Cs with TD-DFT computed absorptions (red sticks). c, Powder EPR spectrum of 4Cs at 50 K (black line) with simulation (red line (1 Tesla = 10,000 Gauss)). d, Variable-temperature (5–293 K) powder EPR spectra data for 4Cs showing the minor variance of g-values over the temperature range. e, Isothermal magnetization versus field data per Th for 4Cs at 100 K, 150 K, 200 K, 250 K and 300 K from 0–7 Tesla showing the uniform diamagnetic response. f, Isothermal magnetization versus field data per Th for 5 at 100 K, 150 K, 200 K, 250 K and 300 K from 0–7 Tesla showing the uniform normal diamagnetic response. Error bars for e and f are not shown for clarity (see Supplementary Figs. 106 and 110–113 for further details).

Source data

Full size image

The UV/vis/NIR spectra of 4M in DME all exhibit two broad absorptions before the onset of strong charge transfer bands that extend into the UV region (Supplementary Figs. 85–93 and Supplementary Table 4). For example, for 4Cs (Fig. 4b), absorptions at 16,950 cm−1 (590 nm, ε = 1,450 M−1 cm−1) and 24,390 cm−1 (410 nm, ε = 596 M−1 cm−1) are observed. These features are not present in the UV/vis/NIR spectrum of 1 and are absent when samples of 4M are re-recorded after exposure to air, suggesting that they are associated with the Th–Th bonding in 4M. Indeed, PBE0 TD-DFT calculations on 4′ suggest that these absorptions correspond to transitions from the 6d-based SOMO to vacant thorium orbitals of predominantly 5f and 7s character (Supplementary Fig. 118 and Supplementary Table 10). Focusing on the ~590 nm feature, for 4M, the average inter-valence charge transfer Γav. parameter (Γ = 1 − (Δν1/2/Δν1/2°)) is 0.64, consistent with a Robin–Day Class III formalism28,29 and full valence delocalization as suggested by the DFT calculations. The Γav. value for 4M compares to values of 0.26–0.29 (Class II) for [{Ln(C5Pri5)(μ-H)}3(μ3-I)2] (Ln = Y, Gd)30, which are reminiscent of 3 and 4M, suggesting more extensive delocalization in 6d than 5d trimetallo clusters.

Variable-temperature X-band EPR spectra of powdered and frozen solution 4M are all similar (Supplementary Figs. 94–102 and Supplementary Tables 5–7). Focusing on powdered 4Cs, near to axial spectra are found (Fig. 4c) with two major features of gx = gy (g⊥) = 1.98 and gz (g||) = 1.94. There is some temperature-dependent variance of signal strength and exact g-value, with a slight increase in values as the temperature is lowered, but the spectra consistently have g⊥ > g|| (Fig. 4d). DFT EPR calculations on 4′ predict gx = 1.955, gy = 1.958 (g⊥ = 1.957) and gz (g||) = 1.911, in good agreement with experiment and correctly returning g⊥ > g||. All the experimental and computed g-values correspond to effective magnetic moments of 1.7 μB for 4M consistent with the theoretical value of 1.73 μB for an S = 1/2 d1 ion (assuming g = 2).

The EPR spectra of 4M exhibit g⊥ > g||, whereas in mono-thorium(III) EPR spectra31,32,33,34,35,36,37,38,39, the g-values are similar but the ordering is reversed, that is, g|| > g⊥. In mono-thorium(III) compounds, the unpaired electrons reside in \(d_{z^2}\)-type MOs that are parallel to their three- or fourfold principal rotation axes, whereas in 4M, the electron resides in an MO that results from constructive overlap of three \(d_{z^2}\) orbitals that are perpendicular to the threefold principal rotation axis of 4′. That the g-values of 4M have an opposite ordering to monometallic thorium(III) complexes supports the valence-delocalized description of 4M. If the unpaired electron in 4M resided on the C8H8 ligands, then a complex feature with multiple hyperfine components centred at g = 2 would be observed40,41. Furthermore, if the unpaired electron were of 5f character, its g-value would be very different and not observable over the higher temperature range owing to rapid relaxation26.

The small increases in g-values as the temperature is reduced provide additional insight into the Th–Th bonding in 4M. Contraction of metal–ligand interatomic distances on cooling should increase the ‘crystal field’, thereby rendering the 1/ΔE term smaller and hence the shift in g-values from ge should decrease, as observed experimentally. In the MO treatment of trimetallo clusters, the anionic ligands define the first-order interactions and the metal–metal bonds are a second-order effect42. Cooling will therefore primarily shorten and strengthen the Th–COT and Th–Cl bonds. However, the g-values are a direct reporter of excited states that are mixed into the SOMO by spin–orbit coupling under the influence of an applied magnetic field, and the SOMO is Th–Th bonding character and largely ‘blind’ to the Th–COT and Th–Cl interactions. Thus, the EPR data are consistent with the presence of Th–Th bonding, even as a second-order interaction, although of course it should be acknowledged that many factors can influence g-values.

Magnetic characterization

Although EPR spectroscopy demonstrates the S = 1/2 paramagnetic nature of 4M, in a 1 Tesla (1 Tesla = 10,000 Gauss) external field, super-conducting quantum interference device magnetometry reveals no net first-order Zeeman paramagnetic susceptibilities and no second-order Zeeman temperature-independent paramagnetism (Supplementary Figs. 103–107). Samples were scrupulously weighed (Supplementary Table 8), and 4Cs was measured as a powder and eicosane-immobilized powder revealing agreement to within 5.4% ruling out any influence of the eicosane (Supplementary Fig. 108). Analysis of the magnetometric data revealed average standard uncertainties of ~5% in magnetization measurements, which is essentially the error of the magnetometer (Supplementary Figs. 110–113). Isothermal magnetization (M) versus field (H) data (100–300 K) for 4M over the range 0–7 Tesla (Fig. 4e) reveal negative linear slopes (R2 = 0.9997–0.9999) with net molar diamagnetic susceptibilities of −1,400 × 10−6 cm3 mol−1 to −1,800 × 10−6 cm3 mol−1 per complex, which is up to four times the anomalous diamagnetic susceptibilities exhibited by [Pt13Hn] (n = 18, 38) superatoms9, and can be compared with predicted standard Pascal’s constant diamagnetic correction values43 for 4M of −692 × 10−6 cm3 mol−1 to −712 × 10−6 cm3 mol−1. The magnetization values (300 K) per thorium atom of −30.5 cm3 Gauss mol−1 to −42.1 cm3 Gauss mol−1 at 7 Tesla (Fig. 4e) are similar to the magnetization per platinum atom for [Pt13Hn] superatoms9. The residual diamagnetism after removal of non-thorium atom contributions for 4M is 11–17 times that expected per thorium ion and overall the diamagnetic responses of 4M are increased 97–160% compared with expected values (Supplementary Table 9). By contrast, M versus H data for 1 (300 K) are within 1.6% of the expected value from Pascal’s constants (−245 × 10−6 cm3 mol−1 versus −249 × 10−6 cm3 mol−1, respectively) with a magnetization per thorium atom of only −16.2 cm3 Gauss mol−1 at 7 Tesla (Supplementary Fig. 109). We examined the M versus H data for the trithorium(IV)-oxo cluster [{Th(η8-C8H8)(μ-Cl)2(μ3-O)}3(Cs)2(DME)3] (5) (Fig. 4f and Supplementary Fig. 114), a fully characterized decomposition product isolated during our preliminary attempts to obtain 4M (Supplementary Materials and Methods and Supplementary Figs. 4, 34–36, 64, 82–84 and 92). At 300 K, we find a net molar diamagnetic susceptibility of −731 × 10−6 cm3 mol−1 (R2 = 0.9998) for 5 that is within 4.8% of the value predicted from Pascal’s constants (−697 × 10−6 cm3 mol−1) and a magnetization per thorium atom of only −16.9 cm3 Gauss mol−1 at 7 Tesla, thus confirming that the anomalous diamagnetism of 4M does not just result from having three thorium ions in close proximity.

Ring current and magnetism calculations

Plotting the anisotropy of induced current density (AICD) of 4′ at the same isovalue as that of 3′ (0.015 a.u.) reveals essentially no induced current density vectors within the trithorium core of 4′ (Fig. 5a), whereas this is present for 3′ (Fig. 5b), reflecting their one- and two-electron natures, respectively. However, the AICD plot of 4′ reveals that ring currents are localized around the Th3Cl6 core, with additional C8H8 contributions, and that the current vectors for the three thorium ions operate in concert. Gauge-including magnetically induced current (GIMIC) calculations return current densities (j(r)) for 4′ in agreement with the AICD calculations. GIMIC finds that 4′ sustains a net diatropic current of 1.81 nA T−1, which is 1.92 nA T−1 more diatropic than the current of −0.11 nA T−1 computed for the S = 0 neutral cluster [{(η8-C8H8)Th(μ-Cl)2}3] (6, using the same coordinates as 4′) (Supplementary Figs. 121 and 122 and Supplementary Tables 11 and 12).

Fig. 5: Computed AICD vectors for 4′ and 3′ and GIMIC of 4′ and 6.
figure 5

a, AICD plot for 4′. b, AICD plot for 3′. c, GIMIC plot of 4′ showing diatropic (red) and paratropic (blue) components. d, GIMIC plot of 4′ showing only the diatropic (red) components. e, GIMIC plot of 6 showing only the diatropic (red) components. f, Induced current density streamlines for 4′. The AICD plots are rendered at the 0.015 a.u. isosurface level and the GIMIC representations are plotted with modulus of j(r) isovalues of 0.025 a.u. for diatropic (red) and paratropic (blue) regions. The streamlines vector magnitude colour scale bar is in a.u.

Full size image

The j(r) of 4′ produce a complex interplay of paratropic and diatropic currents across topologically diverse 4′. The overall j(r) topology of the Th3Cl6 unit is diatropic, and that is bounded by a paratropic region and then the outer sides of the C8H8 rings provide an additional layer of diatropism (Fig. 5c). However, probing local j(r) effects is deterministic, being conditional on integration box selection. Therefore, we computed the net isotropic magnetic susceptibility of 4Cs. While the computed value of −729.59 × 10−6 cm3 mol−1 for 4Cs is approximately half the experimental value of 4Cs, given that these magnetic susceptibility calculations are limited to scalar (spin–orbit neglected) relativistic effective core potentials and are computed as the derivative of the energy in the limit of zero magnetic field, that the calculation returns a substantially negative (diamagnetic), rather than expected positive (paramagnetic), susceptibility for an S = 1/2 molecule is striking, especially when considering that diamagnetism is normally weak and paramagnetism is normally a dominant effect. For comparison, the analogous value for hypothetical diamagnetic S = 0 [M(2.2.2-cryptand)]+[6] of −557.65 × 10−6 cm3 mol−1 is less diamagnetic than the value computed for S = 1/2 4Cs, emphasizing the otherwise counterintuitive increase in diamagnetic response when an electron is added to the Th3Cl6 core.

Thus, the experimental and computed data present a consistent picture. The ground state of 4′ exhibits a valence-delocalized three-centre-one-electron SOMO, which results from the constructive overlap of three \(6d_{z^2}\)-based orbitals to produce a HOMO that has the appearance of an s orbital. When 4′ is placed in an external applied magnetic field, the SOMO ground state is polarized from the centre of 4′ across the Th3Cl6 unit, generating concerted ring currents over the latter. In turn, that produces exalted diamagnetism44,45 (Fig. 5d), whose delocalized continuum is disrupted at the thorium-chloride intersections when the valence-delocalized electron is absent in hypothetical S = 0 6 (Fig. 5e), consistent with the reduction of diamagnetic susceptibility when the unpaired electron is removed from 4′ in silico. While a single unpaired electron would be expected to align parallel to the external applied field, the global ring current around the Th3Cl6 core evidently results in substantial antiparallel alignment9. Thus, 4′ is diatropic despite its S = 1/2 nature, consistent with the magnitude of exalted diamagnetism further supported by the current streamlines (Fig. 5f). To put the exalted diamagnetism (Λ; Supplementary Table 9) of 4M into context44, their Λ values (not including the in-principle ‘cancelled’ χP contribution of 1,250 × 10−6 cm3 mol−1) are 688 × 10−6 cm3 mol−1 to 1,108 × 10−6 cm3 mol−1, which compares to values of −4 × 10−6 cm3 mol−1, 0 cm3 mol−1, 13.7 × 10−6 cm3 mol−1, 34 × 10−6 cm3 mol−1, 267.4 × 10−6 cm3 mol−1 and 640.1 × 10−6 cm3 mol−1 for 1 (Supplementary Fig. 109), cyclohexane46, benzene46, 5 (Supplementary Fig. 114), [14]annulene46 and [18]annulene46, respectively. Exalted diamagnetism is normally a hallmark of closed-shell jellium superatoms9,47,48,49. However, it has also been predicted for open-shell superatoms as jellium aromaticity6, where the aromaticity results from the highest superatomic shell being half-filled with same-spin electrons that presents extra stability; this differs from spherical aromaticity50 since it results from delocalization of electrons inside metal clusters, whereas the latter results from delocalization of electrons on the surface of a sphere. The characterization data support the molecular thorium valence-delocalized description of 4M, where the large radial distribution of 6d-orbitals evidently enables valence delocalization and superatom character in an external applied field, in contrast to transition metal superatoms that tend to delocalize using s orbitals because their radially less expansive d orbitals remain localized, arguing against spherical aromaticity, metallic character, conductance and Knight shift effects. The superatom contributions to the exalted diamagnetic responses of 4M correspond to ~50–62% of their anomalous diamagnetism and being S = 1/2, 4M has a 1S1 magic number6, which is consistent with the SOMO of 4′ having the overall appearance of an s orbital.

Conclusion

We have reported the synthesis and characterization of three mixed-valence trithorium nanoclusters, which each feature a singly occupied three-centre-one-electron valence-delocalized trithorium metal–metal bond. These S = 1/2 clusters are paramagnetic, but in external applied magnetic fields, they exhibit diamagnetic susceptibilities owing to exalted diamagnetism overwhelming the intrinsic paramagnetic character, which experimentally evidences open-shell jellium aromatic character. Exalted diamagnetism, which is an experimental observable resulting from aromaticity, is not normally associated with a single unpaired electron, but here with a magic number of 1S1, the valence delocalization enables exalted diamagnetism by the global superatom ring currents in these trithorium clusters. The discovery of actinide open-shell jellium superatoms allows us to classify these one-electron trithorium clusters as superalkali, or even supercoinage, atoms, where for almost a century Group 1 and 11 elements have also been known to exhibit anomalously strong diamagnetism51. This suggests that f-element metal–metal bonding through the superatom concept shares underpinning analogies to other element groups, and is thus poised for further elaboration in the periodic table’s ‘third dimension’.

Methods

General

Experiments were carried out under a dry, oxygen-free dinitrogen atmosphere using Schlenk-line and glove-box techniques. All solvents and reagents were rigorously dried and deoxygenated before use. Compounds were variously experimentally characterized by single-crystal and powder X-ray diffraction, NMR, FTIR, Raman, UV/vis/NIR and EPR spectroscopies, SQUID magnetometry and elemental analysis. Compounds were theoretically probed using CCSD, DFT, TD-DFT, ELF, QTAIM, AdNDP, EDDBF, NBO7, AICD, ICSS, GIMIC and EDA calculations. Further details are available in Supplementary Materials and Methods.