Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Zigzag graphene nanoribbons with periodic porphyrin edge extensions

Nature Chemistry volume 17, pages 1356–1363 (2025)Cite this article

Subjects

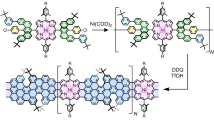
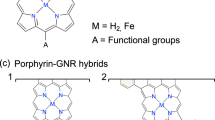
Abstract

Graphene nanoribbons (GNRs) with zigzag edges are promising materials for spintronic devices due to tunable bandgaps and spin-polarized edge states. Porphyrins offer complementary benefits such as desirable optoelectronic properties. Here we combine these features in a hybrid system by means of the on-surface synthesis of zigzag-edge GNRs embedded with porphyrins laterally fused along the ribbon backbone. Using scanning probe methods, we show that this design achieves strong electronic coupling between the porphyrin and the GNR. For transition metal porphyrins, pronounced exchange coupling between distant metal centres is mediated by the π-electron system. Such a hybrid d and π electron ribbon system introduces spin–orbit coupling and magnetic anisotropy to carbon nanomaterials, and holds great promise for coherent electrical control of electron spins.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Prototypical GNRs achieved with atomic precision via on-surface synthesis.
Fig. 2: On-surface synthesis of MPor–3ZGNR (M = 2H, Zn) on Au(111).
Fig. 3: Electronic structure of ZnPor–3ZGNR.
Fig. 4: Engineering the electronic structure of MPor–3ZGNR with noble metal centres.
Fig. 5: Spin coupling of magnetic metal centres in FePor–3ZGNR.

Similar content being viewed by others

Data availability

Data supporting the findings of this study are available within the article and Supplementary Information. The raw data supporting the results of the paper are available on the Materials Cloud repository63 at https://doi.org/10.24435/materialscloud:bw-ph. Crystallographic data have been deposited at the Cambridge Crystallographic Data Centre, under deposition numbers CCDC 2281373 (2HPor–DBA), 2281312 (ZnPor–DBA) and 2391152 (FePorCl–DBA). Copies of the data can be obtained free of charge via www.ccdc.cam.ac.uk/structures/.

References

  1. Chen, Z. et al. Synthesis of graphene nanoribbons by ambient-pressure chemical vapor deposition and device integration. J. Am. Chem. Soc. 138, 15488–15496 (2016).

    Article  CAS  PubMed  Google Scholar 

  2. Chen, C. et al. Sub-10-nm graphene nanoribbons with atomically smooth edges from squashed carbon nanotubes. Nat. Electron. 4, 653–663 (2021).

    Article  CAS  Google Scholar 

  3. Talirz, L., Ruffieux, P. & Fasel, R. On-surface synthesis of atomically precise graphene nanoribbons. Adv. Mater. 28, 6222–6231 (2016).

    Article  CAS  PubMed  Google Scholar 

  4. Yang, X. et al. Two-dimensional graphene nanoribbons. J. Am. Chem. Soc. 130, 4216–4217 (2008).

    Article  CAS  PubMed  Google Scholar 

  5. Cai, J. et al. Atomically precise bottom-up fabrication of graphene nanoribbons. Nature 466, 470–473 (2010).

    Article  CAS  PubMed  Google Scholar 

  6. Clair, S. & de Oteyza, D. G. Controlling a chemical coupling reaction on a surface: tools and strategies for on-surface synthesis. Chem. Rev. 119, 4717–4776 (2019).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  7. Ruffieux, P. et al. On-surface synthesis of graphene nanoribbons with zigzag edge topology. Nature 531, 489–492 (2016).

    Article  CAS  PubMed  Google Scholar 

  8. Gröning, O. et al. Engineering of robust topological quantum phases in graphene nanoribbons. Nature 560, 209–213 (2018).

    Article  PubMed  Google Scholar 

  9. Rizzo, D. J. et al. Topological band engineering of graphene nanoribbons. Nature 560, 204–208 (2018).

    Article  CAS  PubMed  Google Scholar 

  10. Turco, E. et al. Observation of the magnetic ground state of the two smallest triangular nanographenes. JACS Au 3, 1358–1364 (2023).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  11. Mishra, S. et al. Topological frustration induces unconventional magnetism in a nanographene. Nat. Nanotechnol. 15, 22–28 (2020).

    Article  CAS  PubMed  Google Scholar 

  12. Mishra, S. et al. Observation of fractional edge excitations in nanographene spin chains. Nature 598, 287–292 (2021).

    Article  CAS  PubMed  Google Scholar 

  13. Gottfried, J. M. Surface chemistry of porphyrins and phthalocyanines. Surf. Sci. Rep. 70, 259–379 (2015).

    Article  CAS  Google Scholar 

  14. Gilbert, W. et al. On-demand electrical control of spin qubits. Nat. Nanotechnol. 18, 131–136 (2023).

    Article  CAS  PubMed  Google Scholar 

  15. Nowack, K. C., Koppens, F. H. L., Nazarov, Y. V. & Vandersypen, L. M. K. Coherent control of a single electron spin with electric fields. Science 318, 1430–1433 (2007).

    Article  CAS  PubMed  Google Scholar 

  16. Baart, T. A., Fujita, T., Reichl, C., Wegscheider, W. & Vandersypen, L. M. K. Coherent spin-exchange via a quantum mediator. Nat. Nanotechnol. 12, 26–30 (2017).

    Article  CAS  PubMed  Google Scholar 

  17. Pozo, I. et al. Enhanced coherence by coupling spins through a delocalized π-system: vanadyl porphyrin dimers. Chem 10, 299–316 (2024).

    Article  CAS  Google Scholar 

  18. Chen, Z. et al. Phase-coherent charge transport through a porphyrin nanoribbon. J. Am. Chem. Soc. 145, 15265–15274 (2023).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  19. Kinikar, A. et al. On-surface synthesis of edge-extended zigzag graphene nanoribbons. Adv. Mater. 35, 2306311 (2023).

    Article  CAS  Google Scholar 

  20. Gross, L., Mohn, F., Moll, N., Liljeroth, P. & Meyer, G. The chemical structure of a molecule resolved by atomic force microscopy. Science 325, 1110–1114 (2009).

    Article  CAS  PubMed  Google Scholar 

  21. Chen, Q. et al. Porphyrin-fused graphene nanoribbons. Nat. Chem. 16, 1133–1140 (2024).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  22. Deng, J.-R., González, M. T., Zhu, H., Anderson, H. L. & Leary, E. Ballistic conductance through porphyrin nanoribbons. J. Am. Chem. Soc. 146, 3651–3659 (2024).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  23. Li, Y., Jiang, X., Liu, Z. & Liu, Z. Strain effects in graphene and graphene nanoribbons: the underlying mechanism. Nano Res. 3, 545–556 (2010).

    Article  CAS  Google Scholar 

  24. Xiang, F. et al. Planar π-extended cycloparaphenylenes featuring an all-armchair edge topology. Nat. Chem. 14, 871–876 (2022).

    Article  CAS  PubMed  Google Scholar 

  25. Paolesse, R., Nardis, S., Monti, D., Stefanelli, M. & Di Natale, C. Porphyrinoids for chemical sensor applications. Chem. Rev. 117, 2517–2583 (2017).

    Article  CAS  PubMed  Google Scholar 

  26. Liu, Z.-F. et al. Control of single-molecule junction conductance of porphyrins via a transition-metal center. Nano Lett. 14, 5365–5370 (2014).

    Article  CAS  PubMed  Google Scholar 

  27. Xiang, F. et al. On-surface synthesis of chiral π-conjugate porphyrin tapes by substrate-regulated dehydrogenative coupling. J. Phys. Chem. C 123, 23007–23013 (2019).

    Article  CAS  Google Scholar 

  28. Shubina, T. E. et al. Principle and mechanism of direct porphyrin metalation: joint experimental and theoretical investigation. J. Am. Chem. Soc. 129, 9476–9483 (2007).

    Article  CAS  PubMed  Google Scholar 

  29. Xiang, F. et al. Direct observation of copper-induced metalation of 5,15-diphenylporphyrin on Au(111) by scanning tunneling microscopy. Surf. Sci. 633, 46–52 (2015).

    Article  CAS  Google Scholar 

  30. Müllegger, S. et al. Preserving charge and oxidation state of Au(III) ions in an agent-functionalized nanocrystal model system. ACS Nano 5, 6480–6486 (2011).

    Article  PubMed  PubMed Central  Google Scholar 

  31. Eng, M. P., Ljungdahl, T., Andréasson, J., Mårtensson, J. & Albinsson, B. Triplet photophysics of gold(III) porphyrins. J. Phys. Chem. A 109, 1776–1784 (2005).

    Article  CAS  PubMed  Google Scholar 

  32. Cai, J. et al. Graphene nanoribbon heterojunctions. Nat. Nanotechnol. 9, 896–900 (2014).

    Article  CAS  PubMed  Google Scholar 

  33. Chen, Y.-C. et al. Molecular bandgap engineering of bottom-up synthesized graphene nanoribbon heterojunctions. Nat. Nanotechnol. 10, 156–160 (2015).

    Article  CAS  PubMed  Google Scholar 

  34. Power, P. P. Stable two-coordinate, open-shell (d1–d9) transition metal complexes. Chem. Rev. 112, 3482–3507 (2012).

    Article  CAS  PubMed  Google Scholar 

  35. Rubio-Verdú, C. et al. Orbital-selective spin excitation of a magnetic porphyrin. Commun. Phys. 1, 15 (2018).

    Article  Google Scholar 

  36. Meng, X. et al. Controlling the spin states of FeTBrPP on Au(111). ACS Nano 17, 1268–1274 (2022).

    Article  PubMed  PubMed Central  Google Scholar 

  37. Li, J. et al. Survival of spin state in magnetic porphyrins contacted by graphene nanoribbons. Sci. Adv. 4, eaaq0582 (2018).

    Article  PubMed  PubMed Central  Google Scholar 

  38. Liu, B. et al. An iron-porphyrin complex with large easy-axis magnetic anisotropy on metal substrate. ACS Nano 11, 11402–11408 (2017).

    Article  CAS  PubMed  Google Scholar 

  39. Yu, M., Yang, S., Wu, C. & Marom, N. Machine learning the Hubbard U parameter in DFT+U using Bayesian optimization. npj Comput. Mater. 6, 180 (2020).

    Article  CAS  Google Scholar 

  40. Himmetoglu, B., Floris, A., de Gironcoli, S. & Cococcioni, M. Hubbard-corrected DFT energy functionals: the LDA+U description of correlated systems. Int. J. Quantum Chem. 114, 14–49 (2014).

    Article  CAS  Google Scholar 

  41. Ternes, M. Spin excitations and correlations in scanning tunneling spectroscopy. New J. Phys. 17, 063016 (2015).

    Article  Google Scholar 

  42. Hahn, J. R. & Ho, W. Single molecule imaging and vibrational spectroscopy with a chemically modified tip of a scanning tunneling microscope. Phys. Rev. Lett. 87, 196102 (2001).

    Article  CAS  PubMed  Google Scholar 

  43. Giessibl, F. J. The qPlus sensor, a powerful core for the atomic force microscope. Rev. Sci. Instrum. 90, 011101 (2019).

    Article  PubMed  Google Scholar 

  44. Gross, L. et al. High-resolution molecular orbital imaging using a p-wave STM tip. Phys. Rev. Lett. 107, 086101 (2011).

    Article  PubMed  Google Scholar 

  45. Yakutovich, A. V. et al. AiiDAlab—an ecosystem for developing, executing, and sharing scientific workflows. Comput. Mater. Sci. 188, 110165 (2021).

    Article  CAS  Google Scholar 

  46. Pizzi, G., Cepellotti, A., Sabatini, R., Marzari, N. & Kozinsky, B. AiiDA: automated interactive infrastructure and database for computational science. Comput. Mater. Sci. 111, 218–230 (2016).

    Article  Google Scholar 

  47. Hutter, J., Iannuzzi, M., Schiffmann, F. & Vandevondele, J. Cp2k: atomistic simulations of condensed matter systems. Comput. Mol. Sci. 4, 15–25 (2014).

    Article  CAS  Google Scholar 

  48. Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).

    Article  CAS  PubMed  Google Scholar 

  49. Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104 (2010).

    Article  PubMed  Google Scholar 

  50. Goedecker, S., Teter, M. & Hutter, J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B 54, 1703–1710 (1996).

    Article  CAS  Google Scholar 

  51. VandeVondele, J. & Hutter, J. Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases. J. Chem. Phys. 127, 114105 (2007).

    Article  PubMed  Google Scholar 

  52. Hapala, P. et al. Mechanism of high-resolution STM/AFM imaging with functionalized tips. Phys. Rev. B 90, 085421 (2014).

    Article  CAS  Google Scholar 

  53. Giannozzi, P. et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 29, 465901 (2017).

    Article  CAS  PubMed  Google Scholar 

  54. Prandini, G., Marrazzo, A., Castelli, I. E., Mounet, N. & Marzari, N. Precision and efficiency in solid-state pseudopotential calculations. npj Comput. Mater. 4, 72 (2018).

    Article  Google Scholar 

  55. Dudarev, S. L., Botton, G. A., Savrasov, S. Y., Humphreys, C. J. & Sutton, A. P. Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA+U study. Phys. Rev. B 57, 1505–1509 (1998).

    Article  CAS  Google Scholar 

  56. Panchmatia, P. M., Sanyal, B. & Oppeneer, P. M. GGA+U modeling of structural, electronic, and magnetic properties of iron porphyrin-type molecules. Chem. Phys. 343, 47–60 (2008).

    Article  CAS  Google Scholar 

  57. Ali, M. E., Sanyal, B. & Oppeneer, P. M. Electronic structure, spin-states, and spin-crossover reaction of heme-related Fe-porphyrins: a theoretical perspective. J. Phys. Chem. B 116, 5849–5859 (2012).

    Article  CAS  PubMed  Google Scholar 

  58. Tersoff, J. D. & Hamann, D. R. Theory of the scanning tunneling microscope. Phys. Rev. B 31, 805–813 (1985).

    Article  CAS  Google Scholar 

  59. van Setten, M. J. et al. The PseudoDojo: training and grading a 85 element optimized norm-conserving pseudopotential table. Comput. Phys. Commun. 226, 39–54 (2018).

    Article  Google Scholar 

  60. Perdew, J. P., Ernzerhof, M. & Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 105, 9982–9985 (1996).

    Article  CAS  Google Scholar 

  61. Adamo, C. & Barone, V. Toward reliable density functional methods without adjustable parameters: the PBE0 model. J. Chem. Phys. 110, 6158–6170 (1999).

    Article  CAS  Google Scholar 

  62. Lin, L. Adaptively compressed exchange operator. J. Chem. Theory Comput. 12, 2242–2249 (2016).

    Article  CAS  PubMed  Google Scholar 

  63. Xiang, F. et al. Zigzag graphene nanoribbons with periodic porphyrin edge extensions. Materials Cloud https://doi.org/10.24435/materialscloud:bw-ph (2025).

  64. Eroshin, A. V., Koptyaev, A. I., Otlyotov, A. A., Minenkov, Y. & Zhabanov, Y. A. Iron(II) complexes with porphyrin and tetrabenzoporphyrin: CASSCF/MCQDPT2 study of the electronic structures and UV–Vis spectra by sTD-DFT. Int. J. Mol. Sci. 24, 7070 (2023).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  65. Antalík, A. et al. Ground state of the Fe(II)-porphyrin model system corresponds to quintet: a DFT and DMRG-based tailored CC study. Phys. Chem. Chem. Phys. 22, 17033–17037 (2020).

    Article  PubMed  Google Scholar 

Download references

Acknowledgements

This research was supported by the Swiss National Science Foundation under grant no. 212875, the NCCR MARVEL, a National Centre of Competence in Research funded by the Swiss National Science Foundation (grant no. 205602), the Werner Siemens Foundation (CarboQuant), the Max Planck Society, ERC grant nos. NANOGRAPH and 2DMATER, EU Project GENIUS, the EC under Graphene Flagship (grant no. CNECT-ICT-604391), the Hundred Talented Program of the Chinese Academy of Science, Natural Science Foundation of Zhejiang Province (grant no. LZ24B020006), Natural Science Foundation of China (grant no. 22405284) and start-up funding at the Chinese University of Hong Kong, Shenzhen (grant no. UDF01002468). C.A.P. acknowledges the Swiss Supercomputing Centre (CSCS) for computing resources (project s1267, lp83). F.X. thanks the Deutsche Forschungsgemeinschaft (DFG) for a Walter-Benjamin Fellowship (project grant no. 452269487) and the SNSF Swiss Postdoctoral Fellowship (grant no. 210093). Y.G. and Z.Q. acknowledge Humboldt Research Fellowships from the Alexander von Humboldt Stiftung. K.M. acknowledges a fellowship from Gutenberg Research College, Johannes Gutenberg University Mainz.

Author information

Author notes

  1. These authors contributed equally: Feifei Xiang, Yanwei Gu, Amogh Kinikar.

Authors and Affiliations

  1. nanotech@surfaces Laboratory, Empa - Swiss Federal Laboratories for Materials Science and Technology, Dübendorf, Switzerland

    Feifei Xiang, Amogh Kinikar, Nicolò Bassi, Andres Ortega-Guerrero, Oliver Gröning, Pascal Ruffieux, Carlo A. Pignedoli & Roman Fasel

  2. Materials Tech Laboratory for Hydrogen and Energy Storage, Ningbo Institute of Materials Technology & Engineering, Chinese Academy of Sciences, Ningbo, P. R. China

    Yanwei Gu

  3. Synthetic Chemistry, Max Planck Institute for Polymer Research, Mainz, Germany

    Yanwei Gu & Klaus Müllen

  4. School of Science and Engineering, Guangdong Basic Research Center of Excellence for Aggregate Science, The Chinese University of Hong Kong, Shenzhen (CUHK-Shenzhen), Shenzhen, P. R. China

    Zijie Qiu

  5. Department of Chemistry, Biochemistry and Pharmaceutical Sciences, University of Bern, Bern, Switzerland

    Roman Fasel

Authors
  1. Feifei Xiang
    View author publications

    Search author on:PubMed Google Scholar

  2. Yanwei Gu
    View author publications

    Search author on:PubMed Google Scholar

  3. Amogh Kinikar
    View author publications

    Search author on:PubMed Google Scholar

  4. Nicolò Bassi
    View author publications

    Search author on:PubMed Google Scholar

  5. Andres Ortega-Guerrero
    View author publications

    Search author on:PubMed Google Scholar

  6. Zijie Qiu
    View author publications

    Search author on:PubMed Google Scholar

  7. Oliver Gröning
    View author publications

    Search author on:PubMed Google Scholar

  8. Pascal Ruffieux
    View author publications

    Search author on:PubMed Google Scholar

  9. Carlo A. Pignedoli
    View author publications

    Search author on:PubMed Google Scholar

  10. Klaus Müllen
    View author publications

    Search author on:PubMed Google Scholar

  11. Roman Fasel
    View author publications

    Search author on:PubMed Google Scholar

Contributions

A.K., R.F., P.R. and K.M. conceived of this project. Y.G. synthesized the precursors under the supervision of Z.Q. and K.M. F.X., A.K. and N.B. performed the scanning probe microscopy measurements. F.X. analysed the scanning probe microscopy data under the supervision of P.R. and R.F. F.X., A.O.-G., O.G. and C.A.P. performed the DFT calculations and theoretical analyses. F.X. and R.F. wrote the original draft. All the co-authors participated in the scientific discussions and in reviewing and editing the paper.

Corresponding authors

Correspondence to Carlo A. Pignedoli, Klaus Müllen or Roman Fasel.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Chemistry thanks Ping Yu and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Differential conductance dI/dV measurements for ZnPor-3ZGNRs segments of increasing length.

(a) STM images of ZnPor-3ZGNR dimer (NZnPor = 2), trimer (NZnPor = 3), tetramer (NZnPor = 4), pentamer (NZnPor = 5) and hexamer (NZnPor = 6). The length of ZnPor-3ZGNR is defined by the number N of ZnPor units in the hybrid ribbon. The color dots in each STM image refer to the tip positions where the dI/dV spectra were taken. (b) dI/dV spectra taken from dimer to hexamer. The color of each spectrum corresponds to the color of the dots shown in (a). The arrows highlight the frontier states that define the bandgap. Both the HOMO (developing into the valence band, VB) and the LUMO (developing into the conduction band, CB) move towards the Fermi level as the length of the ZnPor-3ZGNR increases. From the pentamer onwards, the HOMO / VB resonance disappears from the spectrum due to its dispersive character. The LUMO / CB position saturates at 0.2 eV in the hexamer. (c) Comparison of experimental (Exp) and DFT calculated (DFT_GP refers to gas phase calculations, DFT_AuSub refers to calculations with Au(111) substrate) bandgaps of ZnPor-3ZGNR dimer to hexamer. Although the calculated band gaps are underestimated by DFT, the trend of decreasing band gap as ribbon length increases is well reproduced. (a) U = −1.5 V, I = 100 pA for dimer to hexamer.

Extended Data Fig. 2 Nc-AFM images and differential conductance dI/dV maps of ZnPor-3ZGNR with different lengths.

Nc-AFM image (first column) and experimental CH dI/dV maps (second to fifth column) of (a) dimer, (b) trimer, (c) tetramer, and (d) hexamer acquired with a CO-functionalized tip. Scanning parameters: (a)-(d) nc-AFM images: U = 0.01 V, I = 250 pA before switching off the feedback. dI/dV maps: I = 500 pA, bias voltages are shown on top of each map.

Extended Data Fig. 3 DFT calculations for Zn-porphine (ZnPor) in gas phase, performed at the PBE level of theory.

(a) Geometry-optimized ZnPor in gas phase. Black, white, blue and grey balls represent carbon, hydrogen, nitrogen and zinc, respectively. (b) Calculated molecular orbitals, evaluated in a plane 3 Å above the molecule. The HOMO and HOMO-1 are close in energy. The LUMO consists of two degenerate orbitals.

Extended Data Fig. 4 Spin-polarized DFT calculations.

The calculated band structure, density of states (DOS) (broadening: 0.05 eV) and LDOS maps of (a) pristine 3ZGNR with primitive unit cell, (b) pristine 3ZGNR in supercell, and (c) strained 3ZGNR. The supercell of the pristine 3ZGNR considered in (b) has been chosen to contain the same number of units as the unit cell of the strained 3ZGNR in (c). In order to maintain the strain pattern consistent with that of the ZnPor-3ZGNR, the strained 3ZGNR model in (c) was built by removing the Por units from the geometry optimized ZnPor-3ZGNR. The unsaturated carbon atoms were then passivated with hydrogen atoms. During geometry optimization of the resulting structure, the backbone of the 3ZGNR was fixed, allowing only the hydrogen atoms to relax. Simulated LDOS maps and spin density maps are shown in the third column. These were evaluated in a plane 3 Å above the ribbon.

Extended Data Fig. 5 Projection of the states of a 12-unit long ZnPor-3ZGNR onto the frontier orbitals of a ZnPor molecule.

Left: Calculated band structure from an infinite ZnPor-3ZGNR using QE code. The corresponding DOS (yellow) is shown on the right. The DOS of an infinite ZnPor-3ZGNR is rescaled to have better visualization. Right: The projected DOS (pDOS) of ZnPor-3ZGNR dodecamer onto HOMO-1 (blue), HOMO (dark blue), LUMO (red) of ZnPor and pDOS of ZnPor-3ZGNR dodecamer (grey). The ZnPor-3ZGNR dodecamer was calculated in periodic boundary condition at the Γ point using the CP2K code. The dodecamer calculation is equivalent to a unit-cell calculation with 12 k-points. Comparing to the calculated band structure and DOS from an infinite hybrid ribbon, ZnPor units show major contribution to CB + 1 and VB-1 in the hybrid ribbon. The LUMO and HOMO of ZnPor become highly dispersive after fusing to 3ZGNR, implying the formation of large π-extension across ZnPor units and 3ZGNR in the hybrid system.

Extended Data Fig. 6 On-surface synthesis of 2HPor-3ZGNRs.

(a) On-surface synthetic route to 2HPor-3ZGNR using 2HPor-DBA precursor. (b) STM image of 2HPor-DBA on Au(111) after heating to 415 K for 30 min. The precursors have undergone debrominative aryl-aryl coupling and formed 2HPor-3ZGNR polymers on the surface. (c) 2HPor-3ZGNR is obtained through cyclodehydrogenative coupling by heating the sample to 620 K for 30 min. High-resolution STM images of 2HPor-3ZGNR with AuPor units, scanned at (d) 0.1 V and (e) −1.13 V. (f) CH nc-AFM image of the 2HPor-3ZGNR with AuPor units shown in (d) and (e). (g) Chemical structure of the ribbon segment imaged in (f). Black, white, blue and red balls represent carbon, hydrogen, nitrogen and metalated gold atoms, respectively. Scanning parameters: (b) U = 0.1 V, I = 100 pA. (c) U = −1.5 V, I = 100 pA. (d) U = 0.1 V, I = 100 pA. (e) U = −1.13 V, I = 100 pA. (f) The tip position is defined on top of the 3ZGNR at U = 0.005 V, I = 150 pA before turning off the feedback.

Extended Data Fig. 7 DFT calculated band structure and local density of states of MPor-3ZGNRs (M = 2H, Zn, Au) in gas phase.

Chemical structure of (a) 2HZnPor-3ZGNR, (d) ZnPor-3ZGNR, and (g) AuPor-3ZGNR. The calculated band structure of (b) 2HZnPor-3ZGNR, (e) ZnPor-3ZGNR, and (h) AuPor-3ZGNR at PBE level of theory. The valence bands and conduction bands for each system are marked as VB-1, VB, CB and CB + 1, respectively. In AuPor-3ZGNR, due to the electron transfer from the Au center to the Por-3ZGNR ligand, the previous CB of Por-3ZGNR is fully occupied and moves below the Fermi level. Thus the VB-1, VB, CB and CB + 1 for Por-3ZGNR are marked as B-1, B-2, B-3 and B-4. The calculated wave function squared frontier bands at the Γ point for (c) 2HZnPor-3ZGNR, (f) ZnPor-3ZGNR and (i) AuPor-3ZGNR, evaluated in a plane 3 Å above the ribbon (FWHM broadening = 0.1 eV).

Extended Data Fig. 8 Spin-polarized DFT calculations of density of states of 13-unit long 2HPor-3ZGNR with one metalated AuPor unit on Au(111).

(a) Geometry optimized model of the 2HPor-3ZGNR with one AuPor unit on Au(111). Black, white, blue, red, and yellow balls represent carbon, hydrogen, nitrogen, the metalated Au, and surface Au atoms, respectively. (b) Calculated DOS (broadening: 0.05 eV) of the 2HPor-3ZGNR with one AuPor (grey shaded area) on Au(111). The projected orbitals on to the Au center in AuPor (green shaded area), the carbon backbone of the AuPor unit (marked by arrow in (a), blue line in DOS map) and the 2HPor unit (marked by arrow in (a), pink line in DOS map) are shown in the map. The Au state is located in the unoccupied region, indicating an electron donation to the ligand. (c) Simulated LDOS maps for the energies indicated by dashed lines in (b). The LDOS maps at −0.05 eV, 0.08 eV, and 0.2 eV were simulated with FWHM broadening of 0.02 eV, the rest using FWHM broadening of 0.2 eV (LDOS evaluated in a plane 3 Å above the ribbon). The same LDOS maps are also shown in Fig. 4(e).

Extended Data Fig. 9 On-surface synthesis of FePor-3ZGNR.

(a) On-surface synthetic route to FePor-3ZGNR using FePorCl-DBA precursors. While there is a Cl atom attached to the Fe center of the as-synthesized FePor-DBA precursor, degassing of the compound under UHV conditions detaches Cl before actual precursor sublimation. (b) Overview STM image of the sample after annealing to 570 K for 15 min. FePor-3ZGNR is fully planarized. (c) High-resolution STM images of FePor-3ZGNRs of different lengths, specified by the number NFePor of precursor units. (d) dI/dV spectra taken from dimer (NFePor = 2) to hexamer (NFePor = 6), at locations indicated by the colored dots in (c). The arrows indicate the position of detected resonances. As judged from dI/dV maps taken at corresponding energies (see Supplementary Fig. 17), resonances 1, 2, 5 and 6 exhibit the typical LDOS features of the VB-1, VB, CB and CB + 1, respectively, of the Por-3ZGNR backbone, as also observed for the ZnPor-3ZGNR. Resonance 3 and 4 are specific to the FePor-3ZGNR, that is they are not observed in ZnPor-3ZGNR. Scanning parameters: (b) U = −1.5 V, I = 100 pA. (c) U = −1.5 V, I = 300 pA.

Extended Data Fig. 10 DFT calculation of Fe in FePor-3ZGNR with different spin configurations and electron occupation in Fe.

(a) Spin configuration considered for the Fe(II) in the porphine core. (b) Using the FePor-3ZGNR structure optimized within PBE level of theory, we use single point calculations with DFT + U (U = 4.4 eV) to determine the spin configuration per Fe atom. The most stable spin configuration is S = 1 per Fe atom. This result is in agreement with previously reported DFT calculations64,65. (c) Scheme of electron occupation in Fe 3 d orbitals with DFT + U (U = 4.4 eV). The two Fe atoms in the FePor-3ZGNR unit cell are specified as Fe1 and Fe2 respectively. \({d}_{{z}^{2}}\) and \({d}_{{yz}}\) are singly occupied, giving the total spin of S = 1 in each FePor unit.

Supplementary information

Supplementary Information

Synthetic procedures, Supplementary Figs. 1–31, Spectroscopic Data Figs. 32–51, Tables 1–6 and refs. 1–9.

Supplementary Data 1

Crystallographic data for 2HPor–DBA; CCDC reference 2281373.

Supplementary Data 2

Crystallographic data for ZnPor–DBA; CCDC reference 2281312.

Supplementary Data 3

Crystallographic data for FePorOMe–DBA; CCDC reference 2391152.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xiang, F., Gu, Y., Kinikar, A. et al. Zigzag graphene nanoribbons with periodic porphyrin edge extensions. Nat. Chem. 17, 1356–1363 (2025). https://doi.org/10.1038/s41557-025-01887-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41557-025-01887-9

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing