Main

The interaction between fluids and rocks plays a critical role in numerous geological processes within Earth’s lithosphere. These interactions are closely linked to earthquake cycles1 and crustal metamorphism2, both of which impact lithosphere stability3, as well as distribution of heat and mass4. They are also essential in subsurface energy extraction and storage5, the formation of mineral deposits6 and environmental geosciences7. Fluid-mediated mineral reactions, particularly at mid-ocean ridges and subduction zones, regulate elemental cycles, including the deep carbon cycle, which influences the return of carbon to the surface. This process is vital for maintaining long-term atmospheric CO2 levels and, consequently, Earth’s habitability8,9.

Near-surface sedimentary rocks have typically well-connected, fluid-filled pore networks10 that facilitate geothermal energy extraction11 and hydrogen storage12. Similarly, fracture networks within the shallow to mid-crust are essential for the transport of aqueous fluids13, impacting mineral deposit formation14. Although fracture-dominated flow may prevail volumetrically, a spectrum of reaction-transport phenomena exists. This spectrum spans from macroscopic fractures down to microscopic nanopores, which facilitate larger volume interconnections, serve as pore throats and are instrumental in initiating fractures2,15,16,17,18. Fluid distribution becomes sporadic deeper within the crust and the upper mantle, that is, at depths past the brittle–ductile transition19. However, even low-permeability rocks at depth can be modified over large volumes via transient reactive transport processes15. During these processes, nanoscale fluid pathways spontaneously emerge from mineral dissolution and precipitation16,20. This highlights the critical importance of incorporating nanopore dynamics into geological models to accurately quantify fluid transport and rock alteration processes.

Fluids confined to nanometric spaces exhibit properties that are markedly different from bulk fluids21. Research has shown that when fluids are confined at the nanoscale, their properties change. These effects include changes to their equation of state22, phase behaviour23,24 and dielectric permittivity25,26. As a result, solute reactivity is different from what is expected under bulk conditions27. The dynamics between confined and bulk fluids may also lead to nonlinear and novel phenomena in fluid–rock interactions. However, recent advancements in thermodynamic calculations of fluid geochemistry and mineral solubilities have largely overlooked the effects of nanoconfinement on fluid–rock interactions within the solid Earth28.

In this Article, we demonstrate that nanoscale fluid pathways are ubiquitous in rocks. We explore the effects of confinement on water’s key ion carrying capability, its dielectric permittivity, for conditions representative of the shallow crust to subduction zones, that is, ambient up to 5 GPa and 700 °C. By integrating our calculated permittivities into geochemical models, we show how nanoscale confinement impacts the fundamental constraints that control fluid–rock interactions.

Nanoporosity in the lithosphere

The presence of nanopores will affect both total porosity and surface area available for fluid–rock interactions. For example, a single, 10 cm wide fracture within a cubic metre of rock provides a surface area of 2 m². However, if even just 1% of the rock’s volume is composed of nanopores with individual diameters of 10 nm, the total surface area available for reaction increases dramatically to 6 million m². Such small pores are common in shallow subsurface materials, where 40% of the total porosity in soils is less than 100 nm (refs. 29,30) and the most common size of pores in this range is 2 nm (ref. 31). They are also frequently found in natural clay-based systems, with 80% of total porosity in shale rocks arising from pores that are less than 50 nm in size32. By contrast, far less is known about deep lithospheric nanoporosity, where nanopores, often reaction-induced16,20, may be vital for fluid and mass transport in low-permeability environments lacking open macropores and fracture networks. Small-angle neutron scattering measurements (Methods) demonstrate that sandstones, dolostones, basalts, peridotites and serpentinites, representing a range of different lithospheric rock units, all contain nanopores, including pores smaller than 20 nm (Fig. 1a). This is confirmed by transmission electron microscopy imaging (Fig. 1b–g), which shows the various morphologies nanopores can adopt in different materials such as serpentine, feldspar, clay, silicate glass and quartz. Interconnectedness is strongly suggested by the fractal nature of the pore-size distribution (Fig. 1a), facilitating fluid access and movement within nanoporous domains. In addition, the trend of smaller, more-prevalent pores aligns with observations from shallower rocks, underscoring the widespread presence and dominance of nanoporosity across various rock types. Thus, confinement effects should be present across the range of fluid–rock interactions of interest in Earth’s lithosphere.

Fig. 1: Unveiling nanoporosity in Earth’s lithosphere.
figure 1

a, Small-angle neutron scattering results illustrating the widespread occurrence of nanopores (less than 100 nm) in rocks spreading the entire lithosphere, from sandstones and dolostones to basalts, peridotites and serpentinites. The red rectangle denotes the information area shown in the inset. b–g, Transmission electron microscopy images depicting the presence of nanopores in crystalline rocks (serpentine (b,c), feldspar (three-dimensional transmission electron microscopy nanotomography, box size: 1.0 × 1.0 × 0.1 µm) (d), clay (e), silicate glass (f) and quartz (g)). Panels adapted from: c, ref. 49 under a Creative Commons licence CC BY 4.0; g, ref. 50 under a Creative Commons licence CC BY-NC-ND 4.0.

Source data

Full size image

Water’s dielectric permittivity in mineral nanopores

The static dielectric permittivity (ε) of water is a critical factor in assessing fluid–rock interactions. It plays a central role in governing ion solvation and the mechanisms of fluid transport33,34,35,36. Building on the theoretical insights from ref. 37 concerning the behaviour of water’s dielectric permittivity under conditions of high pressure (P) and temperature (T), ref. 28 laid the groundwork for the Deep Earth Water (DEW) model. This model represents an improvement in our ability to quantitatively predict fluid behaviour within the lithosphere on the basis of the isotropic properties of bulk water. However, models that predict fluid behaviour may need to be modified when applied to nanoconfined or interfacial settings. In these settings, ε becomes a second-order tensor, which causes the behaviour of permittivity components to differ from that observed in bulk conditions. Importantly, the perpendicular component of water’s permittivity (ε⊥) plays a crucial role in the solvation and transport of ions, while the parallel component (ε‖) influences transport dynamics along the walls of pores17.

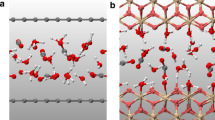
To determine the dielectric permittivity of water within geological nanoporous environments, we used a synergistic approach that combined density functional theory, classical molecular dynamics and statistical mechanics (Methods). Our research focused on water’s behaviour when constrained between different mineral surfaces, spaced by distance H (Fig. 2a). We selected minerals such as calcite (CaCO3), quartz (SiO2) and brucite (Mg(OH)2) for this study. In this context, brucite, a basic layered hydroxide, was used as a simplified model for magnesian phyllosilicates which, as serpentines, chlorites and smectites, occur across a spectrum of rock types, from igneous to sedimentary. Along with calcite and quartz, brucite represents key components commonly found in Earth’s lithosphere. Our analysis focused on the influence of ε⊥ as it is expected to have a first-order effect on mineral solubility17. However, ε‖ also deviates from bulk behaviour under nanoconfinement (Extended Data Fig. 1).

Fig. 2: Molecular dynamics simulations depicting water confinement and estimation of its dielectric permittivity in mineral nanopores.
figure 2

a, Snapshot of the simulation box showing water confined between two calcite slabs. (red, O; white, H; green, Ca; dark grey, C). b, At ambient conditions, confinement of water between the mineral surfaces exerts a substantial impact on ε⊥, crucial for ion solvation and mineral solubility, demonstrating the importance of this effect compared with bulk water. c,d, The perpendicular permittivity of water in 3 nm and 10 nm brucite pores from our molecular dynamics simulations compared with bulk water behaviour calculated by the DEW model at elevated temperatures (at constant P = 1 GPa) (c) and pressures (at constant T = 500 °C) (d). Data are presented as mean values ± standard deviations (1σ) from five molecular dynamics (MD) simulations with different initial conditions.

Source data

Full size image

To calculate ε⊥, we applied a fluctuation equation derived from linear response theory (Methods). The efficacy of this method is supported by the observation that ε⊥ aligns with the bulk-like water properties at the centre of the pore (Extended Data Fig. 2). This figure also highlights the spatial variation of ε⊥, leading us to integrate across the distance H for an averaged value. Using this approach, we examined the average ε⊥ at various H scales, similar to those found in mineral nanopores shown in Fig. 1. The channel sizes we investigated ranged from 1 to 20 nm.

Under nanoconfinement at ambient conditions, ε⊥ shows a considerable difference from the bulk water dielectric constant (εb) (Fig. 2b). As the channel narrows, ε⊥ consistently decreases for all confining minerals, where the extent of this reduction is dependent on the investigated mineral surfaces and bulk crystal structures. Brucite shows the highest permittivity in confined water for any channel size, whereas quartz displays the lowest permittivity values. While our models focused on slit-shaped pore channels, a reduction in dielectric permittivity is also anticipated in pores with curved or more complex geometries17. Therefore, emerging phenomena due to the reduction of dielectric permittivity are expected to be similar.

The decrease in ε⊥ can be attributed to two factors: the reduced rotational freedom of water molecules near interfaces and the low dielectric response of the confining minerals. Highly perturbed interfacial water layers, typically on the nanometre scale, exhibit reduced polarizability because surface-induced alignment of water molecules restricts their ability to reorient, thereby lowering the dielectric response (Extended Data Fig. 3). At the same time, the confining solid materials, possessing a notably lower permittivity, generate an anisotropic dipolar electric field. This leads to an excluded-volume effect. Water molecules are displaced from areas where they would normally contribute positive dipole correlations expected in bulk water. These long-range dipole correlations can extend over several nanometres38. On the basis of these physical mechanisms, and the apparent universality of dielectric reduction in nanoconfinement, the degree of reduction may vary slightly depending on the specific surface and confining solid. Typically, the dielectric permittivity starts to deviate from bulk values at confinement around 100 nm, with considerable reductions observed in pores smaller than 30 nm (refs. 25,26).

To explore how increasing T and P impact confined water’s permittivity, we analysed systems with an H of 3 and 10 nm in brucite under conditions up to 700 °C and 5 GPa (water density variations for different systems under various P–T conditions are presented in Extended Data Fig. 4.). Figure 2c illustrates the ε⊥ of water confined within these nanopores, at T up to 700 °C and a constant P of 1 GPa compared with the expected permittivity of bulk water at equivalent conditions based on the DEW model. Although the confined water mirrors the overall trend expected for bulk water behaviour of a decrease in ε⊥ with rising T, the values of ε⊥ under confinement remain smaller than that of bulk water. Similar behaviours are also found between confined and bulk water with increasing P up to 5 GPa at a constant temperature of 500 °C, where confined water ε⊥ remains offset to lower values compared with the bulk (Fig. 2d). Notably, at ambient conditions, water confined in brucite nanochannels exhibits the most minor, albeit still considerable, deviation from bulk water behaviour compared with quartz and calcite (Fig. 2b). We focused on high P–T simulations for brucite confinement. However, due to the universal nature of dielectric reduction observed in quartz and calcite (Fig. 2b), and supported by studies on other materials25,26,38, we expect similar behaviour across a wide range of minerals in different geological settings, with only minor variations. Consequently, since confined water consistently behaves differently from the properties predicted for bulk water, our results demonstrate that we cannot use εb to accurately represent the behaviour of water in rocks with prevalent nanoporosity (Fig. 1).

Pore-size-dependent effects on mineral solubility

Our research reveals a drop in ε⊥ for water molecules confined at the nanometre-length scale between mineral surfaces, representing nanopores. Given the importance of water’s ε in determining the solvation and mobility of charged and polar ions/molecules in geological systems, we henceforth investigated how nanoconfinement of fluids may affect mineral solubility.

Numerous studies have explored mineral solubility within nanoporous environments, yet a comprehensive predictive model remains undeveloped39. Previous research, applying classical nucleation theory18, suggested that ion clustering is less likely in these confined spaces, hindering nucleation. This inhibition of precipitation aligns with considerations that crystals with high surface-to-volume ratios tend to have higher solubilities than their bulk counterparts40,41. However, more recent studies highlighted the contrasting effects of pore wall interactions—noninteracting walls42 can hinder precipitation, while interacting walls may promote it. Building on this, our focus shifts to the influence of the confining medium, specifically the minerals composing the pore walls. We argue that the energetic properties of the bulk mineral predominantly govern its solubility behaviour. Hence, we examine the impact of changes in the physical properties of water on mineral solubility while acknowledging that multiple factors ultimately control the precipitation process. As such, we incorporate our pore-size-dependent dielectric properties of water into an enhanced Helgeson–Kirkham–Flowers (HKF) equation of state, now integrated within an open-source computational platform43, to compute the thermodynamic properties of minerals and related aqueous species at elevated P and T. This approach (Methods) is analogous to the DEW model and enables us to predict the solubilities of minerals, here quartz and calcite (Fig. 3).

Fig. 3: Nanoconfinement effect on mineral solubility at elevated P–T conditions.
figure 3

a,b, Quartz solubility versus temperature (a) and pressure (b). c,d, Calcite solubility versus temperature (c) and pressure (d). Data points show experimental mineral solubilities from refs. 44,45, with 1σ and 2σ uncertainties for calcite and quartz, respectively. Nanoconfinement decreases solubility in all cases.

Source data

Full size image

Geochemical models using εb of water predict that both quartz and calcite become slightly more soluble in water as P and T increase (Fig. 3). These predictions agree with mineral solubilities obtained from bulk experiments with mineral powders with no expected nanoconfinement effects44,45. On the contrary, when we use our dielectric permittivity values for nanoconfined water, we find that mineral solubilities are predicted to be up to half an order of magnitude lower in 10 nm pores. Therefore, changes in the water related to nanoconfinement will have a knock-on effect on mineral solubility due to the non-bulk properties of water as a solvent. In general, minerals appear to have lower solubilities in nanoconfined water under conditions relevant for the lithosphere, which could be a pivotal factor influencing fluid–rock interactions and mass transport mechanisms.

Given the universal nature of nanoconfinement effects21,46 and the consistent patterns of dielectric reduction observed both in this study and across various solid materials25,26 under diverse P–T conditions, our findings probably apply to a wide range of minerals and natural materials in different geological settings. Our simulations indicate that minerals generally exhibit reduced solubility in nanoconfined fluids under lithospheric conditions, spanning from low-temperature hydrothermal environments to the extreme conditions of subduction zones. This reduction in solubility could be a key factor influencing fluid–rock interaction mechanisms. Moreover, even if the predictions made here are eventually found to require refinement, they underscore that current geochemical models, including those based on the HKF equation of state, fail to adequately capture the behaviour of confined interfacial environments. This emphasizes the necessity for developing new modelling and experimental approaches.

Consequences for fluid–rock interactions in the lithosphere

By revealing the marked deviation in water’s physical properties under nanoconfinement—specifically, its dielectric permittivity and the resultant effects on mineral solubility—our study challenges the prevailing paradigms that govern geochemical models of fluid–rock interactions. Linking pore-size-dependent geochemistry with nanoscale transport mechanisms16,21 is crucial for developing a more comprehensive nanoscale reactive transport model. Integrating this model into existing large-scale porous media frameworks will allow for more accurate predictions of fluid–rock interactions. This approach deepens our quantitative understanding of key processes such as mineral reactivity (including dissolution, nucleation and growth), ion speciation dynamics and the mass transport mechanisms that are essential drivers of geological phenomena.

Our modelling results indicate that we may need to rethink the dynamics of carbon cycling within Earth’s lithosphere. As a cornerstone of processes in the deep Earth carbon cycle, a change in the solubility of carbonates would directly influence the mobility of C during fluid–rock interactions at depth, changing the predicted C release from, for example, subduction zones8,9,47,48. This observation is just one of many implications that arise from our research findings. The distinct properties of fluids under nanoconfinement necessitate the integration of nanopore and interface dynamics into geochemical models to capture the complexities of these interactions accurately. This observation not only holds for classic nanoporous environments such as clays and soils, but is expected to apply to a wide range of lithospheric rocks. The integration of nanoscale phenomena is essential to bridge the gap between controlled laboratory experiments, which often rely on bulk fluid properties, and the heterogeneous, nanoconfined environments encountered in natural geological settings. Such an approach promises to enhance our predictive capabilities concerning mineral solubility, fluid composition and the overall geochemical evolution of the lithosphere.

Methods

Small-angle neutron scattering

Small-angle neutron scattering data for a variety of rocks, including sandstone51, dolostone52, basalt53, peridotite54 and serpentinite55, have been obtained from specified references. For data analysis, the MATSAS56 script-based program in MATLAB was utilized. This program employs the polydisperse spherical pore model to derive structural details from the scattering data of porous materials. Such details include specific surface area, porosity and pore-size distribution.

Electron microscopy

Mineral nanopores were visualized through electron microscopic imaging, utilizing a combined approach of focused ion beam scanning electron microscopy (TFS Helios G3 NanoLab) and (scanning) transmission electron microscopy (TFS Talos 200FX and TFS Spectra 300). Transmission electron microscopy nanotomography data were acquired using a TFS Tecnai 20, and three-dimensional tomographic reconstruction was performed with TomoJ, an ImageJ plug-in57. The serpentinite samples originated from ODP Leg 209 site 1274, while the feldspar samples were collected from the Larvikite intrusion complex in Norway, and the silicate glass and clay samples are derived from published experiments58,59. All electron microscopic analyses were carried out at the Electron Microscopy Centre of Utrecht University.

DFT

Density functional theory (DFT) calculations were performed using a linear combination of atomic orbitals basis set as implemented in the all-electron code CRYSTAL (2017 release)60,61 where the atoms were described using basis sets in the literature (calcium62, carbon62, oxygen62, magnesium63, hydrogen64 and silicon65,66). The global hybrid B3LYP exchange-correlation functional67,68 was used throughout all calculations without further modifications. The mixing of non-local Fock and semi-local exchange provides a reliable representation of electronic and structural properties of a range of oxide compounds69,70,71. For calcite and β-quartz, long-range dispersion corrections were included using the semiempirical D3 approach of refs. 72,73,74 with Becke–Johnson damping. For brucite, the D2 approach with the C6 coefficient and van der Waals atomic radii set to preceding noble gas values was utilized, as proposed by ref. 75. Bulk calcite was described in the R-3c (number 167)76, bulk quartz in the P6222 (number 180)77 and bulk brucite in the P-3m1 (number 164)78 crystallographic space group, as obtained from the American Mineralogist Crystal Structures Database79. The Coulomb and exchange series are summed directly and truncated using overlap criteria with thresholds of 10–8, 10–8, 10–8, 10–8 and 10–16 as described previously60,80. The condition for the self-consistent field convergence was set to 10–8 au on the total energy difference per cell between two subsequent cycles. Reciprocal space was sampled according to a regular sublattice with a shrinking factor (input IS) of 7 for quartz and calcite and 11 for brucite. Within DFT, the surfaces were modelled as two-dimensional periodic slabs, where no three-dimensional periodicity was imposed. To characterize the surface, the surface energy (γ), indicative of thermodynamic stability, is calculated using the following expression:

$$\gamma =\frac{E\left(n\right)-n\,{E}_{{{\mathrm{bulk}}}}}{2A}$$
(1)

where E(n) is the energy of the slab containing n layers, Ebulk is the energy of the bulk, and A is the area of the slab. The (10–14) surface of calcite, (10–11) surface of quartz and (001) surface of brucite were chosen for further analysis due to their non-polar nature and observed dominance in experimental measurements. The calculated surface energies read 0.49 J m–2, 2.07 J m–2 and 0.04 J m–2 for the calcite (10–14), quartz (10–11) and brucite (001) surfaces, respectively, corresponding well to earlier calculated values81,82,83. These surface geometries have been utilized as a starting point for subsequent molecular dynamics simulations.

MD simulation

All MD simulations were executed in the LAMMPS package84. Equations of motion are integrated with the velocity Verlet algorithm with a time step of 1 fs. The temperature was kept constant by using a Nosé–Hoover thermostat85 with a damping parameter of 0.1 ps. After equilibration for 2 ns, all systems were run for 20 ns in a canonical ensemble (NVT). The cut-off radius for the short-range interactions was set to 1 nm for the Lennard–Jones (LJ) potential and 1.2 nm for the Coulomb potential. A particle–particle particle–mesh solver86 was used to calculate long-range electrostatic interactions. Periodic boundary conditions were applied in the x and y directions. The Yeh−Berkowitz slab correction87 was employed, which excludes the long-ranged electrostatic contributions from the periodic image cells in the z direction. Atom trajectories were gathered every 0.1 ps to get enough data to compute the permittivity. Confined systems are made up of two parallel mineral slabs that are spaced apart by H in the z direction, which varies from 1 to 20 nm in our simulations. The mineral slabs were kept static during the simulation, preventing their positions from being updated. This approach eliminates conformational fluctuations at high pressures and temperatures88 and prevents artificial distortions caused by the slab’s limited thickness89. Reference 90 showed that the density and velocity profiles of fluid that is nanoconfined using rigid and flexible calcite walls are nearly identical. Moreover, our results on interfacial water structures reveal that, in calcite confinement, the first water layer is located 2.33 Å from the calcium carbonate plane, with the second layer at 3.63 Å. In brucite confinement, the first layer is positioned at 2.4 Å from the surface. These findings are consistent with both experimental and simulation results from studies such as refs. 91,92, reinforcing the accuracy of our model. In addition, maintaining a rigid substrate provides a stable reference plane for integrating atomic charge and perpendicular polarization density profiles along the z axis during simulations, which is critical for accurately calculating perpendicular permittivity. The SPC/E model93 was applied for water simulation, with the SHAKE algorithm94 maintaining its rigidity. This model has proved reliable under extreme P–T conditions and outperforms other models in capturing electronic polarizability and the dielectric properties of water37,95,96. For each mineral system, five MD simulations with varied initial positions and velocities were conducted to average the results. We used water density in the channel to indirectly maintain the desired pressure at any temperature (already fixed by the Nosé–Hoover thermostat). By adjusting the number of water molecules in the nanochannel, we replicated the desired pressure, allowing us to simulate each P–T condition. To do so, an iterative insertion/deletion method determined the number of water molecules per system to match the density at the channel’s centre with experimental liquid water density (Extended Data Fig. 4)38. Calcite, brucite and quartz were selected as confining minerals, each initially relaxed via DFT simulations. A (10–14) plane-terminated calcite crystal formed the calcite surface, with dimensions of 4.1 × 4.0 nm (x–y plane) and a thickness of 3.2 nm. The brucite slab, terminated on the (001) plane with hydrogen, and the quartz slab, terminated on the (10–11) plane with oxygen, measured 4.1 × 4.4 × 3.2 nm and 4.4 × 4.0 × 3.1 nm, respectively. The channel width was determined by the centre-to-centre distance between the outermost oxygen atoms of the top and bottom surfaces97. The reference position z = 0 corresponds to the position of the bottom slab’s outer layer oxygen atoms in all cases98. Calcite surfaces remained non-hydroxylated, a valid assumption since water dissociation on the (10–14) calcite surface is not anticipated99,100, occurring only at surface defects101. We utilized the ref. 102 force field for leveraging LJ potentials instead of Buckingham potentials to characterize van der Waals interactions. This selection allows for smoother integration with various mineral and fluid force fields and facilitates the simulation of larger systems owing to the more rapid computation of LJ energies than exponential Buckingham potentials. Although ref. 102 utilized the TIP3P water model in developing their force field, ref. 91 demonstrated its compatibility with the SPC/E model, which generates a water structure on the calcite surface that closely resembles that produced by TIP3P. For brucite and quartz simulations, the ClayFF force field103 was adopted. ClayFF is used under high P–T conditions as well (for example, ref. 104). In addition, keeping the solid walls static during the simulations prevents any unintended effects from brucite behaviour under elevated P–T conditions.

Perpendicular permittivity calculation

In confined environments, unlike in bulk water, the dielectric permittivity of water exhibits tensorial characteristics. Specifically, within a slit channel, the component of the dielectric permittivity tensor perpendicular to the channel walls (z direction) changes spatially with z. This variation can be quantitatively described by a fluctuation equation derived from statistical mechanics and linear response theory105,106, which calculates the local inverse perpendicular permittivity:

$${\varepsilon }_{\perp }^{-1}\left(z\right)=1-\beta {\varepsilon }_{0}^{-1}[{\left\langle {\,p}_{\perp }\left(z\right){P}_{\perp }\right\rangle }_{0}-{\left\langle {\,p}_{\perp }\left(z\right)\right\rangle }_{0}{\left\langle {P}_{\perp }\right\rangle }_{0}]$$
(2)

where β is thermal energy inverse, \({\left\langle \ldots \right\rangle }_{0}\) represents the ensemble average when there is no external electric field, p⊥(z) is the perpendicular fluid polarization density at position z, and P⊥ is the fluid total polarization’s perpendicular component, which is provided by:

$${P}_{\perp }=A{\int }_{0}^{H}{p}_{\perp }\left(z\right){{\mathrm{d}}z}$$
(3)

The perpendicular polarization density at position z is determined as:

$${p}_{\perp }(z)={\int }_{0}^{z}{\rho }_{e}\left({z}^{{\prime} }\right){\mathrm{d}}{z}^{{\prime} }$$
(4)

where \({\rho }_{e}(z)\) is the fluid atomic charge density profile in the z direction calculated using a binning method with 0.01 Å resolution.

When the preceding equation is integrated over the entire channel, the average inverse perpendicular permittivity is obtained as:

$${\varepsilon }_{\perp }^{-1}=1-\frac{{\left\langle {P}_{\perp }^{2}\right\rangle }_{0}-{\left\langle {P}_{\perp }\right\rangle }_{0}^{2}}{{\varepsilon }_{0}V{k}_{{\mathrm{B}}}T}$$
(5)

where kB is the Boltzmann constant. The fluctuation equations for calculating dielectric permittivity, originally developed by ref. 105 (Ballenegger–Hansen (BH)) for a single slab periodic in the x and y directions, need modification for systems nonuniform in the z direction but periodic in all directions. The correct equation to calculate the perpendicular dielectric permittivity in such systems incorporates the total polarization fluctuations, as outlined in the ref. 107 (Stern–Feller) formula. In our MD simulations, the confined system is periodic in the x and y directions, using a particle–particle particle–mesh solver for long-ranged Coulomb electrostatic interactions. For the z direction, we omit long-ranged electrostatic contributions from periodic image cells, which are not suitable for two-dimensional periodic systems. Reference 87 showed that excluding these contributions in the z direction (a method called Ewald3dc) mirrors the rigorous two-dimensional Ewald summation’s behaviour in a two-dimensional periodic system. Thus, by neglecting image cell contributions in the z direction and maintaining sufficient empty space, the BH formula is effectively applied to calculate perpendicular dielectric permittivity under these specific conditions. Choosing the right boundary conditions and fluctuation formula is crucial for accurate results. Misapplication of the BH equation with Ewald3d or the Stern–Feller equation with Ewald3dc can lead to inaccuracies, particularly in the channel’s centre26.

Parallel permittivity calculation

For systems that are inhomogeneous only in one direction (the z axis, perpendicular to the surface), the locally varying parallel dielectric permittivity can be calculated using principles from statistical mechanics and linear response theory. The applicable fluctuation formula, derived from these principles105, allows for the determination of the parallel dielectric permittivity as it varies along the z direction:

$${\varepsilon }_{\parallel }\left(z\right)=1+\frac{\beta {\varepsilon }_{0}^{-1}}{2}[{\left\langle {{\bf{p}}}_{\parallel }\left({\bf{z}}\right).{{\bf{P}}}_{\parallel }\right\rangle }_{0}-{\left\langle {{\bf{p}}}_{\parallel }\left({\bf{z}}\right)\right\rangle }_{0}.{\left\langle {{\bf{P}}}_{\parallel }\right\rangle }_{0}]$$
(6)

where the vector \({{\bf{p}}}_{\parallel }=(\,{p}_{x},\,{p}_{y})\) represents the in-plane polarization density of the fluid at position z, and \({{\bf{P}}}_{\parallel }\) denotes the parallel component of the total fluid polarization vector. These vectors can be calculated using the molecular dipole moment with the following equations:

$${{\bf{p}}}_{\parallel }\left({{\bf{z}}}_{i}\right)=\frac{1}{A\Delta z}\mathop{\sum }\limits_{j=1}^{N({z}_{i})}{{\bf{\upmu}} }_{\parallel ,\,{\bf{j}}}$$
(7)
$${{\bf{P}}}_{\parallel }=\mathop{\sum }\limits_{j=1}^{N}{{\bf{\upmu}} }_{\parallel ,\,{\bf{j}}}$$
(8)

where \({{\bf{\upmu}} }_{\parallel ,\,{\bf{j}}}=(\,{\mu }_{x,\,j},{\mu }_{y,\,j})\) represents the parallel component of the jth dipole, N denotes the total number of water molecules, \(N({z}_{i})\) signifies the number of molecules positioned at \(z=\,{z}_{i}\) inside the channel, and \({z}_{i}\) indicates the location of the ith bin with thickness \(\Delta z\). Since the system is homogeneous in the x and y directions, one can neglect the \({\left\langle {{\bf{p}}}_{\parallel }\left({\bf{z}}\right)\right\rangle }_{0}.{\left\langle {{\bf{P}}}_{\parallel }\right\rangle }_{0}\) term in equation (6). Thus, by applying the definitions provided in equations (7) and (8), we can find the parallel dielectric permittivity as follows:

$${\varepsilon }_{\parallel }\left({z}_{i}\right)=1+\frac{\beta {\varepsilon }_{0}^{-1}}{2A\Delta z}\left[\mathop{\sum }\limits_{j=1}^{N\left({z}_{i}\right)}\left\langle {\mu }_{\parallel ,\,j}^{2}\right\rangle +\mathop{\sum }\limits_{j=1}^{N\left({z}_{i}\right)}\mathop{\sum }\limits_{k\ne j}^{N}\left\langle {{\bf{\upmu}} }_{\parallel ,\,{\bf{j}}}.{{\bf{\upmu}} }_{\parallel ,\,{\bf{k}}}\right\rangle \right]$$
(9)

In this equation, the first summation pertains to the dipole–dipole self-correlation within a bin, and the subsequent one refers to the cross-correlation between the dipoles of the ith bin and the entire system108.

Thermodynamic equilibrium modelling

For thermodynamic equilibrium modelling, the open-source PyGCC package43, written in Python, was adapted to incorporate our updated dielectric constants into the revised HKF equation of state for calculating the thermodynamic properties of aqueous species109. This involved updating the dielectric constant of bulk water with values from water confined in 3 and 10 nm pores over a temperature range of 100 to 700 °C and a pressure range of 0.1 to 5.0 GPa. In addition, we updated the value of the water dielectric constant while keeping its P–T derivatives unchanged. This decision is supported by the P–T dependency of the perpendicular permittivity (Fig. 2c,d), which indicates that the slope (derivative) of the dielectric constant with respect to P at constant T (or T at constant P) does not systematically change with pore size. Instead, pore size appears to create an offset in the absolute value rather than altering the overall behaviour. On the basis of the updated permittivities reflecting nanoconfinement effects, new thermodynamic databases were created for the Geochemist’s Workbench110 software using PyGCC. The React module within the Geochemist’s Workbench, which uses mass and charge balance constraints to determine equilibrium fluid and mineral compositions, was then used to calculate the solubility of calcite and quartz as a function of temperature, pressure and pore size employing these newly created databases. Unlike quartz, calcite solubility is dependent on the speciation of carbonic acid, which, in turn, depends on solution pH. We thus calculated calcite solubility by first assuming the initial solution contained 10 mmol kg–1 Cl– and very small amounts of Ca++ and HCO3– and calculating pH via charge balance. To this initial solution, we added calcite until equilibrium was achieved, which, in turn permitted the determination of the equilibrium solubility of calcite in terms of Ca++ and HCO3– concentrations as a function of temperature, pressure and pore size. At a constant P of 1 GPa, equilibrium points were calculated for T of 500, 600 and 700 °C, and a line was fitted to the results. Similarly, at a constant T of 500 °C, equilibrium points were calculated for P of 0.5, 1.0 and 3.0 GPa, and a polynomial was fitted to the results. In the case of quartz, whose solubility does not depend on pH below the dissociation constant for silicic acid (that is, at the conditions of interest here), solubility was determined directly by equilibrating quartz with a dilute aqueous solution. Under a constant P of 1 GPa, a sliding T algorithm from 200 to 700 °C was used. At a constant T of 500 °C, individual equilibrium points for P of 0.5, 1.0 and 3.0 GPa were calculated, and a logarithmic function was fitted to the results.