Abstract
Calderas are depressions formed by some of the largest volcanic eruptions. Their long-lived inter-eruptive periods are occasionally interrupted by phases of unrest, in which escalating seismicity, ground deformation and gas emissions raise concerns of potential volcano reawakening. However, interpretation of such physico-chemical signals is complicated by few examples of monitored unrest that culminated into eruption and by our fragmentary understanding of the drivers and timescales of caldera reactivation. Here we show that multi-decadal gas observations at the restless Campi Flegrei caldera in Italy record an unprecedented increase in isotopically light sulfur release from fumaroles since 2018. We then use hydrothermal gas equilibria and numerical simulations of magmatic degassing to propose that such a change in sulfur emissions results from decompression-driven degassing of mafic magma at ≥6 km depth, along with some extent of sulfur remobilization from hydrothermal minerals. Examination of a global dataset indicates that, despite the diversity in eruptive behaviour and tectonic setting, increasing sulfur output may be a common process during unrest escalation at calderas generally. Hence, our observations and models of sulfur behaviour may inform interpretations of unrest and hazard assessment at reawakening calderas and hydrothermal active volcanoes worldwide.
Similar content being viewed by others
Main
Volcanically active regions on Earth are occasionally punctuated by subsided volcanic structures of variable size and age, referred to as calderas1. These often-subcircular depressions are commonly thought to have derived from rapid emptying of magma reservoirs during large-scale effusive to explosive (eventually ignimbrite-forming2) eruptions. Once formed in one or multiple caldera-forming eruption(s), calderas, especially if resurgent3, are sites of episodic intra-caldera eruptions, typically interspersed within repose periods of intense hydrothermal activity4 that can last for centuries or longer3.
Resumption of eruptive activity at reawakening calderas is normally anticipated by above-background changes in seismicity, ground deformation and chemistry/flux of hydrothermal fluid emissions. However, these caldera unrests5,6 are some of the most enigmatic and puzzling volcanic phenomena, especially because they can persist for decades without necessarily culminating into eruption. Hence, while many of the ~100 calderas active in the Holocene epoch have experienced historical unrest5, most of them have not witnessed eruption in the instrumental era, rendering ex-ante identification of possible eruption precursors highly uncertain. Questions remain regarding the driving mechanisms of caldera unrest, and especially on their magmatic7,8 versus hydrothermal9,10 nature.
A remarkable example is offered by the resurgent Campi Flegrei (CF) caldera, in the suburban metropolitan area of Napoli (Italy) (Extended Data Fig. 1). After four centuries of dormancy and subsidence following the 1538 eruption11, CF has experienced unrest since the 1950s, with a net uplift of ∼4 m (ref. 12) total in four main ground uplift episodes (1950–1952, 1969–1972, 1982–1984 and 2000–present), the two most recent of which are associated with intense volcano-tectonic seismicity12. Consensus exists that deformation/seismicity are caused by elastic/brittle response13,14 of the shallow crust to pressure build-up at the base of the hydrothermal system15 (∼3-4 km depth), caused by escalating magmatic fluid transport16. However, debate remains on whether magma is intruding at shallow depth17 or remains stationarily at depth18,19. Therefore, possible unrest evolution, and likelihood of an eruption, remain largely undetermined.
Because magmatic volatiles are critical drivers of unrest16,20,21,22, measuring the chemistry, the isotopic composition and the flux of surface fluid emissions is essential for caldera monitoring6,23. Carbon dioxide (CO2), with minor unreactive species (nitrogen and noble gases), has proved especially useful for tracing the influx of magma-derived volatiles into caldera-hosted hydrothermal systems24,25. However, because these volatiles are poorly soluble in silicate melts, they can be effectively supplied by magmas stalled in the mantle26, and hence an increase in their concentration in surface discharges is not necessarily a hint for increased eruption probability6,18,23. Sulfur, by contrast, is a major magmatic volatile that, due to its lower vapour–melt partitioning coefficient27, is exsolved from the melt at mid- to upper-crustal conditions28, thus becoming a potentially very useful tracer of escalating unrest. As calderas become increasingly restless, hydrothermal minerals29 can remobilize sulfur and contribute, alongside magma-sourced sulfur, to accelerating surface output30,31.
Escalating sulfur at Campi Flegrei
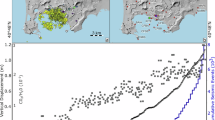
The exceptionally continuous record of fumarole composition at CF (Supplementary Table 1) has been taken previously16,22,25 to identify a remarkable progression towards less-hydrous, more-CO2-rich compositions over the past four decades (Fig. 1a). In addition to some extent of steam condensation in the hydrothermal system16,32, this transition has been interpreted to reflect an increasingly magmatic nature of the fumarolic gas, supported by the convergence of deuterium/hydrogen (D/H) ratios in fumarolic steam towards magmatic values (δD (delta deuterium) values of –10 to –30‰ versus SMOW (standard mean ocean water); Fig. 1b). However, an observation we bring to light is the unprecedented, five times increase in fumarolic sulfur, in the form of hydrogen sulfide (H2S), since early 2018 (Fig. 1c). This increase in fumarolic H2S abundance (Fig. 2) is paralleled by a systematic isotopic shift (Fig. 1c) towards negative sulfur isotope compositions (δ34S < 0 versus Vienna Canyon Diablo Troilite (VCDT)). This isotopic change is even larger than observed33 during the stronger (for rate of uplift and seismicity) 1982–1984 unrest (Fig. 1c). The observed fumarolic changes (Figs. 1 and 2) require that an additional, isotopically distinct source of sulfur has come into play at CF since 2018. We envisage two possible endmember scenarios (hydrothermal versus magmatic) for the involved source process.
Data from Supplementary Table 1. Analytical uncertainty at 1 standard deviation (s.d.) of the mean. a, A progression from H2O-rich (hydrothermal (H)) to CO2-rich (magmatic (M)) compositions is observed. b, Deuterium isotope composition (δD, relative to SMOW) of fumarolic steam evolves to progressively more positive signatures, within the magmatic gas range15,16,25. c, H2S concentrations increase since 2018, paralleled by a negative isotopic shift of the sulfur isotope composition. d, Observed (fumaroles) versus modelled (at equilibrium with hydrothermal pyrite; Methods) gas H2S/CO2 ratios. The excess H2S during 2018–present (and in the 1980s) implies H2S fugacity is not buffered by pyrite during accelerating unrest. e, Volcano-tectonic seismicity (monthly number of events, grey bars; data from INGV Osservatorio Vesuviano) versus the estimated H2S flux from the Solfatara area. This flux is calculated by multiplying the diffuse CO2 output from the Solfatara degassing structure32 by the fumarolic H2S/CO2 ratio (panel d).
The H2O, CO2 and H2S concentrations are scaled by factors 1, 3 and 300, respectively, for presentation purposes. The 1983–2023 fumarole results (Supplementary Table 1) are chronologically distinguished (by colour tones) to emphasize temporal evolution. The 1970 and 1979–1983 results for other CF fumaroles are also shown (Supplementary Information). Fumarole composition is contrasted against (1) the modelled composition of magmatic gases formed during decompressional degassing of trachybasaltic CF melts (Fig. 5); (2) the modelled composition of hydrothermal gases in which H2S fugacity is controlled by S-bearing hydrothermal minerals (pyrite, native sulfur and anhydrite) (Methods); (3) the observed fumarole compositions at eight global calderas/hydrothermal volcanoes that have recently been in a state of unrest (Supplementary Information; YWS, Yellowstone; LVC, Long Valley Caldera; NYS, Nisyros; KU, Kusatsu–Shirane; HA, Hakone; SNG, Sierra Negra; PPR, Planchón–Peteroa; KRB, Kuchinoerabujima); (4) the composition of high-temperature magmatic gases (for data provenance, see Supplementary Information). Note the distinct CF fumarole evolutions in 1983–1987 (towards the hydrothermal pole, H) and 2018–present (towards the magmatic pole, M). The almost linear post-2018 CF fumarole progression can be interpreted to reflect a combination of (1) pure sulfur addition from native S/anhydrite breakdown, caused by exposure of new mineral surface due to fracturing/seismicity (2) mixing with sulfur-rich magmatic gas supplied by magma degassing (by decompression) within the mid-crustal (≥6 km) magmatic plumbing system (Fig. 4).
Sulfur remobilization from hydrothermal minerals
Given the current CF solfatara stage of activity, remobilization of hydrothermal mineral-bounded sulfur is a possible driver for the escalating H2S fumarolic transport (hydrothermal scenario). During the centuries- to millennia-long repose periods of calderas, any sulfur supplied by the magmatic source at depth is typically sequestered in a variety of hydrothermal mineral deposits29,34 that form via reactions between host rocks and magmatic volatiles35. During unrest, hydrothermal conditions are perturbed by escalating magmatic gas transport16 and seismicity, resulting in higher temperature and change in redox conditions. Consequently, sulfur stored in hydrothermal minerals can be remobilized into the hydrothermal gas phase31. At CF, pyrite is the most abundant sulfur-bearing mineral36. Two lines of evidence suggest, however, that pyrite redissolution is an unlikely source for the excess H2S seen at CF since 2018. First, CF hydrothermal pyrite is isotopically heavy (δ34S of 3.3 to 7.4‰ versus Vienna Canyon Diablo Troilite; ref. 36), so that any H2S(g) remobilized (at equilibrium) from pyrite (Methods) would cause shifting of the fumarole H2S to higher δ34S, which is the opposite to what is observed (Fig. 3a). We caution that some isotopically light (δ34S of –11.0 to –0.1‰; Fig. 3a) H2S can potentially be formed from pyrite if its decomposition mechanism involves disproportionation into aqueous sulfate and H2S(g) (Methods). Second, and hence more conclusively, a pyrite origin for the post-2018 excess H2S is inconsistent with hydrothermal gas equilibrium calculations (Methods) that fix the equilibrium H2S/CO2 composition of the hydrothermal gas phase in which H2S fugacity is controlled by pyrite decomposition30. Results of these calculations (Fig. 1d) indicate that modelled and observed (fumarole) compositions match within uncertainty during 2003 to early 2018, supporting validity of the model approach. However, they diverge during the two major unrests of 1982–1984 (and following years) and from mid-2018 onwards (Fig. 1d). We conclude that pyrite equilibria control H2S fugacity during background hydrothermal activity at CF but cannot explain the escalation seen from 2018 onwards. Native sulfur and sulfates (alunite and anhydrite) have also been identified in the CF hydrothermal mineral paragenesis36. Gas–mineral equilibria (Methods) indicate that these minerals are unstable at the CF hydrothermal temperature (T) and pressure (P) conditions (Extended Data Fig. 2), and hence have a strong tendency to decompose to H2S(g). The post-2018 acceleration in H2S release is concurrent with a significant seismicity increase (Fig. 1e). We therefore argue that the seismicity-driven opening of new fractures may have created new gas migration pathways, exposing new mineral surfaces to gas–mineral reactions and causing effective sulfur extraction, from native sulfur and sulfates, into the gas phase. Native sulfur and alunite are abundant in the shallow supergene environment (around the fumaroles), where they form by near-surface oxidation of fumarolic H2S. The sulfur isotopic compositions of these fumarolic incrustations (native sulfur, −5.5 to 0‰; sulfates, −1.7 to −0.2‰; ref. 36) are within the range of that of source fumarolic H2S (Fig. 3a). However, native sulfur and alunite are absent, and anhydrite is rare (too low to be measurable for δ34S), in the deep hydrothermal mineral assemblage36. Since seismicity clusters in this deeper portion of the hydrothermal system (between 1 and 3 km depth; Fig. 4), we cannot exclude, but consider it unlikely, that native sulfur and anhydrite are suitable sources for the post-2018 fumarolic H2S increase.
a–c, The CO2/H2S ratios in Bocca Grande fumaroles plotted versus the sulfur isotope compositions of fumarole H2S (a) and fumarole H2O/H2S ratios (analytical uncertainty at 1 standard deviation of the mean (s.d.)) (b,c). The 2018–2023 fumarole results identify a linear trend that requires addition of excess, isotopically light (<–1.5‰) sulfur from either (1) native sulfur/anhydrite breakdown or (2) sulfur-rich magmatic gases (or a combination of the two). In a, the fields of H2S formed by pyrite breakdown are derived from equations (3), (5) and (11) (Methods). The predicted isotope composition of H2S from native sulfur breakdown is obtained from results of ref. 36 (equilibrium hydrothermal gas composition is derived by combining equations (9), (10) and (13); Methods). In a–c, the magmatic degassing model lines are the same as in Fig. 2 (the predicted sulfur isotope composition of magmatic gases is modelled as shown in Supplementary Data 1 and Methods). The inset (panel c) shows the 2018–2023 regression line (95% confidence interval shown) intersects the magma degassing trends at model degassing run pressures that—depending on model run input conditions—range from 149 to 373 MPa (Supplementary Data 1). In the magmatic hypothesis for the escalating H2S release, the source magma is mafic (trachybasaltic) and undergoes decompressional degassing in the mid-crustal plumbing system, at ≥6 km depth.
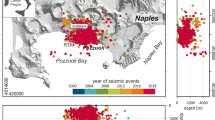
Redrawn according to the stratigraphic model proposed by ref. 38. Two-dimension resistivity model of Solfatara of hydrothermal system resulting from audiomagnetotelluric measurements32 is also reported as a section. High resistivity values mainly indicate gas-phase zones, while low resistivity values reveal zones with presence of liquid, eventually derived from condensation of hydrothermal vapour32. Earthquakes recorded by the Osservatorio Vesuviano seismic network since 2018 are reported as grey circles, whose dimensions are proportional to magnitude.
Mafic magma as the source of sulfur
Second, we consider the hypothesis of a magmatic origin (magmatic scenario) for fumarolic H2S. The post-2018 H2S escalation raises the question whether conditions that would allow active sulfur degassing from the magma have been reached. Decompressional (ascent-driven) sulfur degassing is a complex function of melt composition, the magnitude of change in pressure and temperature, initial volatile content, melt oxidation state and modes of magma ascent/decompression28. Melt inclusion (MI) evidence suggests the CF parental melts are trachybasaltic37. Once applied to these compositions, numerical modelling of magmatic degassing27 (Methods) suggests a deep sulfur degassing behaviour (Fig. 5). Our calculations (Supplementary Data 1) constrain that CF trachybasalts become volatile-saturated at high pressures (from ∼400 to >1,000 MPa for initial CO2 contents of 0.4 to 2 wt%). The CO2-dominated (CO2 molar fraction, \({{{X}}}_{{{\rm{CO}}}_{2}}\) of 0.65–0.82; Fig. 5e) magmatic gas phase that forms at high pressures contains relatively high total S (XS of 0.025 to 0.1; Fig. 5f), suggesting effective removal of sulfur from the melt. Using the maximum sulfur content of ~2,200 ppm in MIs as an estimate for parental melt sulfur content (Extended Data Fig. 3), we find that half of the initial sulfur cargo is lost to gas on decompression-driven degassing at >200 MPa pressure (Fig. 5a), within the >7.5 km deep CF main magma storage zone38,39 (Fig. 4). This gas-phase sulfur is inferred to be a mixture of H2S and SO2 (Fig. 5c). Deep sulfur degassing is consistent with the sulfur-poor compositions of evolved, trachytic to phonolitic, CF melts (Extended Data Fig. 3) that are typically formed (and stored) at shallower depths (≤8 km). Modelling results imply that a magmatic source hypothesis for the post-2018 fumarolic H2S escalation does not require magma transport to shallow levels. Rather, we find that if the observed (post-2018) fumarolic gas compositions are extrapolated to higher sulfur concentrations (Fig. 3b,c), hence minimizing the hydrothermal fluid contribution, they intercept the modelled magmatic gas composition trends at ∼150 MPa pressure (~6 km) in our preferred models (initial CO2 = 2 wt%; melt redox at NNO to NNO + 0.75, where NNO is the nickel–nickel oxide buffer at a magmatic temperature of 1,120 °C; Methods), or deeper (>∼240 MPa, or >~8.5 km) if the magma is CO2-poorer (0.4–0.8 wt%). We caution that, considering errors (Supplementary Data 1) associated with linear regression of the data trend (Fig. 3b,c), combined with uncertainty on initialization parameters (primarily magma redox and CO2 content) and on calibration of the degassing model itself27, the magma source pressure/depth cannot be precisely inferred. However, our results would be indicative of magma ascent at the top, or right above (to as shallow as ~6 km), the ≥7.5 km deep CF magma storage zone38 (Fig. 4).
All data from Supplementary Data 1. The plots illustrate the pressure dependency of equilibrium melt (a) and gas (b–f) inferred from model simulations27 of decompression-driven, closed-system degassing of trachybasaltic CF melts (Methods). Results of nine model runs, initialized at different CO2 contents and redox conditions (Supplementary Data 1), are shown. a, Dissolved sulfur in the melt, demonstrating relatively deep sulfur degassing for CF melts. b, Pressure-dependent evolution of the model magmatic gas CO2/ST ratio (ST, total sulfur). c, Sulfur speciation in the gas phase, indicating that, at pressures higher than 100 MPa, SO2 makes up from <40% at NNO to ~80% at NNO + 0.75, to >95% at NNO + 1.5. This implies that, in the magmatic scenario hypothesis, fumarolic H2S can serve as a proxy of total magmatic sulfur only at condition that the magma source is reduced (~NNO), deep (>100 MPa, or > 4 km) and that any SO2 is converted into H2S during gas expansion and cooling, from magmatic temperature to surface temperature (150–165 °C). d–f, Model-predicted evolution of H2O, CO2 and ST molar fractions in the equilibrium magmatic gas phase. The gas becomes increasingly CO2-rich (and ST-rich) with increasing model run pressure.
To test feasibility of the magmatic hypothesis, we also analysed the sulfur isotopic composition in olivine-hosted trachybasaltic MIs from two of the most mafic eruptions of the recent CF activity37 (Supplementary Table 2). Our results (Fig. 6) constrain the CF magmatic source to have δ34S of ∼–1.7 ± 1.1‰. These δ34S values fall within the mid-ocean-ridge basalt range40, and are isotopically lighter (depleted in 34S) than seen at other arc volcanoes worldwide41,42. The isotopically light sulfur signature of CF parental melts, implied by our MI results, constrain the δ34S values in magmatic fluids between –3.7 and –1.7‰ (Figs. 3a and 6b). Hence, an increased supply of isotopically light magmatic sulfur to the hydrothermal system can explain the observed drop in δ34S of the fumarolic H2S since 2018 (Fig. 1c). Notably, since the modelled gas is a mixture of SO2 and H2S (Fig. 5), while the fumaroles contain only H2S, our results suggest magma-sourced SO2 delivered at depth is quantitatively converted into H2S, hence conserving the total gaseous sulfur δ34S, on cooling (<400 °C) and re-equilibration in the hydrothermal envelope.
a, MI sulfur isotopic composition plotted against sulfur content (measured by secondary ion mass spectrometry; data from Supplementary Table 2). The red band shows the δ34S range of mid-ocean-ridge basalts40. Grey diamonds and crosses are published MI and glass data from arc volcanics in Central America42 and the Cascades41, respectively. The yellow-brown line shows the results of a total least-squares regression fitted to the data, assuming equilibrium closed-system degassing, while the shaded area is 1 standard error of the regression. The large pentagon symbol shows the predicted δ34S of the undegassed melt. Yellow, green and red lines are forward degassing models calculated using Sulfur_X (ref. 27) and combined with sulfur isotope fractionation factors for sulfide-sulfate, H2S-sulfide and H2S-SO2 (Methods; all calculations reported in Supplementary Data 1). Solid, dashed and dotted lines show model runs with variable CO2 contents (2.0, 0.8 and 0.4 wt%). All error bars are 2 s.d. of the mean. b, Same as a but reporting the model evolution of the equilibrium gas sulfur isotope compositions (for closed-system degassing).
A step change in caldera degassing behaviour
The hydrothermal versus magmatic hypotheses are not easy to resolve from our results alone and are not mutually exclusive; rather, the two processes can work in combination since sulfur remobilization would ultimately be driven by heating of the hydrothermal system16,22 caused by escalating magmatic gas supply. Accelerating surface H2S release may, at least in principle, be consistent with a scenario in which the magmatic gas supply is constant, but the hydrothermal system more actively releases sulfur—or becomes more transparent to the magmatic gas supply—because of increasing stretching (by continuous deformation and heating) and fracturing (by escalating seismicity). However, compared with the 2018–present unrest at CF, the 1982–1984 bradyseismic crisis has been much stronger12 for rate of uplift and seismicity, and yet the observed H2S excursion has been far more modest (both chemically and isotopically33; Figs. 1–3). Considering the rarity of anhydrite36 in the deep hydrothermal rocks that compose the main seismogenetic volume (Fig. 4), it seems unlikely fracturing alone—and hence exposure of new sulfur-bearing mineral surfaces—can explain the large, persistent post-2018 excess sulfur excursion (Fig. 1c,d). We hence consider decompressional degassing of mafic magma, on upward migration in the ∼6 to ≥8.5 km depth range (Fig. 4), as the most likely source for the post-2018 excess sulfur. We note that our inferred, gas-based magma ascent interval is consistent with those derived from modelling of post-2018 deformation43 and with local earthquake tomography results44 that point to ascent to depths <8 km as the driver of the ongoing (post-2018) unrest. Ascent of new, volatile-rich magma is also implicated by the observed increase in gas output15. While at least in principle it is possible for a stationary magmatic source to release more gas due to second boiling26,45, any shallow-stored magma in the upper crust would need to be of limited volume (to escape seismological detection), and especially if felsic would hence remain an insufficient source for the large CO2 (ref. 15) and sulfur (Fig. 1e) surface output, due to low volatile content (Extended Data Fig. 3).
Our results are a hint for further evolution of the unrest that is otherwise ongoing for >70 years. Retrospective analysis of the (few available) pre-1980s fumarolic results (Extended Data Fig. 4) indicates that the H2S increase in the fumaroles may have continued, although at a sluggish rate, for more than a century. Yet the post-2018 increase is unprecedented for rate and amplitude, and hence marks a step change in degassing behaviour.
Escalating sulfur during caldera unrest may not be unique to CF. We have identified eight well-monitored, globally distributed calderas/hydrothermal volcanoes (Supplementary Information) for which long-term gas observations are available (Fig. 2). We caution these volcanic systems are very diverse in size, eruptive history and magma composition, making generalization or exportation of interpretations from one system to another not straightforward. Yet analysis of this global dataset (Fig. 2) shows persistence of sulfur-poor, hydrous compositions at calderas (for example, Yellowstone, Long Valley) where unrest has not culminated into eruption. By contrast, progression towards increasingly sulfur-rich fumarole compositions has been observed at volcanic systems (for example, Sierra Negra, Planchón–Peteroa and Kuchinoerabujima) in which unrest has finally escalated (over timescales of years/decades) to eruption. This general behaviour suggests tracking unrest evolution using volcanic gas sulfur can be beneficial for hazard assessment and mitigation not only at CF, but at calderas/hydrothermal volcanoes globally.
Accepting a magmatic hypothesis for escalating sulfur at CF would not provide conclusive evidence that an eruption will necessarily occur, and/or is imminent. Petrology and mineral chemistry results46 indicate calderas typically undergo multiple magma resupply episodes47 before the critical overpressure conditions for eruption initiation are finally reached, perhaps in decades to less than a century48. For example, the last magmatic eruption in ad 1538, for which ground deformation history has been reconstructed in detail11, was anticipated by magma emplacement in the upper crust starting as early as ~100 years before (or potentially more), and by remarkable geophysical/geochemical precursors49. There is today no geodetic/seismological evidence for non-radial, asymmetric ground deformation patterns and upward migrating seismicity50, as inferred for the 1538 eruption preparatory/run-up phase11. In addition, the CF fumaroles are still compositionally far from the manifestly magmatic signatures observed before caldera eruptions elsewhere (Fig. 2). Yet the fact mafic magma may have intruded in the mid-crustal (≥6 km) plumbing system demands any possible action is put in place or intensified to increase preparedness for eruption in this intensively inhabited area (~800,000 people are living inside the caldera). Any further compositional evolution of the fumaroles towards the magmatic gas range (Fig. 2) should be carefully considered as a sign of increased eruption likelihood.
Methods
Fumarole gas composition
The fumarole composition dataset is available in Supplementary Table 1. This dataset is based on periodic (monthly) sampling surveys of the Bocca Grande fumarole (T = 150–165 °C) located inside the Solfatara crater, the largest hydrothermal manifestation of CF. Pre-2022 compositional results have been published elsewhere (ref. 32 and references therein). Samples were collected using standard protocols using pre-evacuated flasks filled with 4 M NaOH solutions51, and were analysed in the laboratory52 by gas chromatography (for major components; Agilent Technologies model 6890N) and mass spectrometry (for water isotopes; Thermo Fisher model deltaXP and Picarro model L2130-i). For measurements of the total sulfur isotopic compositions, 50 ml of NaOH sample solution were collected in a 100 ml volumetric flask. 2 ml of a 30% H2O2 solution were then added, and the resulting mixture was left to rest for about 1 h. Oxygen excess was then removed by boiling the solution. The solution was titrated with HCl 6 M using methyl orange indicator, keeping the solution under stirring and heating to 60 °C to allow the produced CO2 to degas. To precipitate barite, 20 ml of a 10% BaCl2 solution were added to 50 ml of condensate under continuous stirring. The obtained solution was then filtered with 0.42 μm filter, and the precipitated barite was dried at 60 °C in an oven for 24 h. The precipitate was then collected with a Teflon spatula, then weighed (0.80 mg on the basis of the expected sulfur content of approximately 13%) in tin capsules (5 × 9 mm). V2O5 (in 1/5 proportions) was added to catalyse the oxidation reaction of any reduced sulfur species. Sulfur isotope ratios (δ34S) were analysed at Università di Palermo by isotope ratio mass spectrometry (Thermo Scientific Delta V ADVANTAGE) after on-line combustion in an elemental analyser (Thermo Fisher Scientific Flash 2000) connected to the isotope ratio mass spectrometer through a Conflo-IV interface. Sulfur isotope ratios were expressed in conventional δ unit notation as parts per mil deviations from the international standard, VCDT, as follows:
where R = 34S/32S. Samples were calibrated to the VCDT scale using certified reference materials of the International Atomic Energy Agency (IAEA-SO-6: –34.1‰; NBS 127: +20.3‰; IAEA-S-1: –0.30‰; IAEA-SO-5: +0.5‰; NBS 127: +21.1‰). Analytical precision based on the standard deviations of multiple analyses of standards (or a combination of repeated analyses of the samples and standards) was ±0.2‰.
Melt inclusions
Olivine and clinopyroxene phenocrysts were hand picked from tephra of Minopoli2 and Fondo Riccio, the two most mafic eruptions in the recent CF history (Supplementary information). Before MI analyses, hand-picked crystals were inspected under a microscope. Crystals containing glassy MIs were picked and individually mounted in crystalbond adhesive, then polished until exposed. Crystals were then mounted in epoxy and polished and cleaned. Major elements S, Cl, and F contents in glassy MIs and their host crystals were analysed using a Cameca SX100 EPMA at the Department of Earth Sciences, University of Cambridge. All analyses were carried out at 15 kV accelerating voltage. Standards used for analyses were St John’s Island olivine (Mg, for olivine analyses), periclase (Mg, for glass and pyroxene analyses), diopside (Si), jadeite (Na), potassic feldspar (K), fayalite (Fe), corundum (Al), Durango apatite (P), wollastonite (Ca), rutile (Ti), chromium metal (Cr), manganese metal (Mn), nickel metal (Ni), pyrite (S), flourite (F) and halite (Cl). Glasses were analysed using a 15 µm defocused beam. A 5 nA beam current was used to analyse Na, Mg, Al, Si and Ca. Sodium was analysed first using 30 s on-peak counting times; tests before analyses showed no Na mobility using this analytical condition. All other elements were analysed using 80 nA beam current. Counts for Cl, S and F were all recorded for >3 min on a glass sample to confirm that this analytical set-up does not mobilize volatiles. The sulfur peak position was moved for the unknown analyses to 61,375 (10,000 × sinθ) to account for the peak position shift between reduced S (pyrite, at 61,387) and oxidized S (celestine, 61,355). Relative error was 1–4% for major and minor elements, apart from Mn (~6%), increasing to ~10% for F, <6% for S and <3% for Cl. A total of 43 MIs and embayments were analysed. Olivine hosts were analysed using a 5 µm beam diameter, a 20 nA beam current for major elements (Si, Mg, Al) and a 100 nA current for all other trace elements. Clinopyroxenes were analysed using a 60 nA beam current. No Na mobility was observed during clinopyroxene analyses. All results and errors are reported in Supplementary Table 2.
Sulfur isotope ratios (34S/32S) were analysed in selected MIs and embayments (n = 21) at the North East National Ion Microprobe Facility at the Department of Geology and Geophysics, Woods Hole Oceanographic Institute, using a Cameca IMS-1280 instrument. A Cs+ primary beam with a beam current of 200–290 pA and an accelerating voltage of 10 kV was used for the analyses. Secondary ions were accelerated using a sample voltage of –10 kV. A normal-incidence electron gun was used to compensate for sample charging. Before analyses, a 60 s, 10 × 10 µm pre-raster was used to clean the sample surface of any potential contamination. After the pre-raster, the field aperture was centred using the dt(x) and dt(y) transfer plates. The secondary ion beam was then passed through a 4,000 µm field aperture, 80 µm entrance slit and 240 µm exit slit. Analyses were carried out in multi-collection mode using three electron multiplier detectors: L2 (30Si), C (32S) and H2 (34S). Each isotope was analysed using a total of 20 cycles, each consisting of 4 s. Mass resolving power was set at 5,000. Three standards were analysed alongside the unknowns: A36 (Icelandic subglacial glass, 1,680 ppm S), STAP (Icelandic subglacial glass, 530 ppm S) and HAW-16095 (Hawaiian picrite glass, 2,220 ppm S (ref. 42)). These glasses cover nearly the full S range observed in our unknowns (500–2,230 ppm; Fig. 6). We find no correlation between instrumental mass fractionation (IMF) and S content. Measured IMF values, calculated as:
are +8.2‰ for STAP, +7.8‰ for A36 and +8.6‰ for HAW-16095. This agrees with previous observations41 for analyses using EM–EM mono-collection analyses at the North East National Ion Microprobe Facility and differs from other studies42 that used FC–EM multi-collection for their analyses. To quantify the unknown 34S/32S values, we applied an IMF correction using the average IMF measured from the three standards (+8.2‰). This was subtracted from the measured δ34S values. The error of the IMF correction is estimated at 0.4‰ (1σ).
Sulfur contents were quantified by fitting a zero-intercept linear regression between standard S contents and measured 32S/30Si × SiO2 (wt%) values. This regression has a 3% (1σ) relative error. The sulfur background, determined using five olivine repeat analyses, was 0.504 ± 0.024 for 32S/30Si × SiO2, equal to 19 ppm S.
Isotopic signature of H2S from pyrite decomposition
Hydrothermal sulfur minerals can remobilize sulfur to gas phase31,53,54. Pyrite is the most abundant hydrothermal mineral at CF and is found55,56 ubiquitously in the propylitic hydrothermal alteration facies at temperatures >200 °C and in the 0.5–2.5 km depth range, well within (and down to the base of) the hydrothermal system sustaining the Solfatara–Pisciarelli surface gas emissions15. We therefore test the hypothesis that the escalating sulfur transport is caused by pyrite redissolution57, because of changing hydrothermal temperature and redox conditions32, as caused by escalating magmatic gas influx15,58.
The isotopic composition of H2S(g) in isotopic equilibrium with pyrite (\({\updelta}^{34}{\rm{S}}_{{{\rm{H}}_{2}}{\rm{S}}_{{\rm{eq}},{\rm{py}}}}\)) (Fig. 3a) is calculated from:
where δ34Spy is the measured36 isotopic composition of hydrothermal pyrite at CF (δ34S of 3.3–7.4‰ versus VCDT), and \({{\rm{\alpha }}}_{{{\rm{py}}-{\rm{H}}}_{2}{\rm{S}}}\) is the fractionation factor of the pyrite–H2S isotopic exchange reaction (estimated in the 150–400 °C range using equations in ref. 59). Since the term \({1,000\mathrm{ln}{{\alpha }}}_{{{\rm{py}}-{\rm{H}}}_{2}{\rm{S}}}\) (corresponding to the enrichment factor \({{{\varepsilon }}}_{{{\rm{py}}-{\rm{H}}}_{2}{{\rm{S}}}_{({\rm{g}})}}\)) is only 0.1–0.3‰ at the explored conditions, any H2S formed at isotopic equilibrium with pyrite is isotopically heavy (δ34S of 3.3–7.4‰) and hence incompatible with the observed fumarolic H2S isotopic signature (Fig. 3a). We additionally model the isotopic composition of H2S(g) formed by pyrite disproportionation into hexavalent S (aqueous sulfate ion) and reduced S (in H2S(g)), such as:
This reaction may potentially occur if pyrite decomposition takes place in a hydrothermal brine where part of the released sulfur is partitioned into the liquid phase, in which case:
where \({{{\alpha }}}_{{{\rm{SO}}}_{4}^{2-}-{{\rm{H}}}_{2}{\rm{S}}}\) is the dissolved sulfate–gaseous H2S sulfur isotope fractionation factor (taken from ref. 59). This reaction would produce isotopically lighter (δ34S of –11.0 to –0.1‰; Fig. 3a) H2S(g), at least in principle consistent with observations on fumaroles.
Hydrothermal gas equilibria
The C–O–H–S equilibrium composition of a hydrothermal gas phase, whose H2S fugacity is controlled by pyrite hydrolysis, is obtained by solving reaction30:
in which (FeO) corresponds to divalent iron incorporated into an (unidentified) aluminium–silicate hydrothermal mineral (possibly chlorite or epidote) and (H2O) is the aluminium–silicate in its protonated, iron-free form30. By rearranging the equation, the H2S fugacity controlled by reaction involving pyrite and silicate is:
To solve equation (7), temperature is calculated32 from the CO–CO2 equilibrium at typical hydrothermal redox conditions60:
Water and CO2 fugacities are assumed to be controlled by liquid–vapour coexistence30 and by the water-shift reaction61, respectively:
The equilibrium hydrothermal gas H2S/CO2 ratio is computed by dividing fH2S (equation (7)) by fCO2 (equation (10)):
These model-predicted compositions are compared with fumarole compositions in Fig. 1d.
Using a similar approach, we also explored other possible hydrothermal H2S sources, including sulfur remobilization from native sulfur (S0) and anhydrite (CaSO4), using equations:
For which, after rearranging;
This can be combined with equation (10) to infer the equilibrium f H2S/fCO2 ratio controlled by native sulfur. Similarly for anhydrite:
The modelled f H2S/fCO2 and f H2S/f H2O ratios are orders of magnitude higher than the measured ones (Extended Data Fig. 2), reflecting very reducing conditions of the hydrothermal system feeding Solfatara. These calculations imply that native sulfur and anhydrite, if exposed to a feeding magmatic gas phase, can act as H2S sources, hence potentially explaining the excess H2S observed since 2018 (“Pure (hydrothermal) S addition” in Figs. 2 and 3). Anhydrite, in particular, has recently been proposed62 as a potential source of H2S at CF. We caution, however, that this mineral is rare in the deep hydrothermal mineral assemblage, making it a thermodynamically possible, but geologically unlikely, source of H2S.
Magma degassing modelling
We use a numerical magmatic degassing model27 to infer (1) the depth/pressure magma interval over which sulfur is actively degassed from CF melts, (2) the composition of the gas that is delivered at each decompression step of the (model) magma ascent path and (3) by combination with mass-balance calculations and knowledge of the relevant isotope fraction factors, the sulfur isotope composition of the magmatic gas (and of the residual melt). We use Sulfur_X, a model27 designed to reproduce the pressure-dependent evolution of S, CO2, H2O and redox state in coexisting melt and vapour in ascending mafic-intermediate arc magmas. Calculations utilize previously existing COH degassing models (we use a model63 appropriate for alkali-rich mafic melts) alongside an empirical parametrization of vapour–melt sulfur partition coefficients based on experimental data. The model takes two reactions into account during degassing: FeS(m) + H2O(g) → H2S(g) + FeO(m) and CaSO4(m) → SO2(g) + O2(g) + CaO(m). Our calculations are initialized using the major element composition (SiO2 = 47.88; Al2O3 = 16.39; FeOT = 7.76; MgO = 3.96; CaO = 11.29; Na2O = 1.99; K2O = 5.22; P2O5 = 0.76; MnO = 0.17; TiO2 = 0.99; all in wt%) of a trachybasaltic olivine-hosted melt inclusion37 (OL7) from the Fondo Riccio eruption. Melt inclusions from Fondo Riccio are used as inputs for the initial (parental melt) H2O (4 wt%) and S (2,200 ppm; Fig. 6) in our model runs (Supplementary Data 1). We note that the Sulfur_X degassing model27 provides an estimate on the sulfide and sulfate concentrations at sulfide saturation, from which the melt's total S solubility can be calculated. We find that even for our most reduced runs at NNO, S solubility remains at >3,000 ppm, which means the melt would remain undersaturated for sulfide. Consistently, sulfides are not present in the olivine or pyroxene crystals that hosted the studied melt inclusions. Measured CO2 contents in the glass of CF melt inclusions are typically low (generally <0.1 wt%, but certainly <0.3 wt%; refs. 64,65). However, MI records are known to severely underestimate the real (parental melt) CO2 contents because of pre-entrapment (to an exsolved fluid phase) and post-entrapment (to shrinkage bubbles) CO2 loss66. Hence, to cope with uncertainty caused by the poorly constrained initial CO2 content, we run our simulations using a range of parental melt CO2 contents (0.4, 0.8 and 2 wt%; Supplementary Data 1). We consider the 2 wt% scenario the most realistic in view of the CO2-rich nature of Phlegrean (and Italian in general) volcanism64. Magma redox67 is the second largest source of uncertainty in our simulations as it is known to severely impact sulfur speciation (in melt68 and gas69) and hence its degassing behaviour27. Results of phase equilibrium experiments70 on CF trachybasalts, and specifically the similarity of Fe/Mg ratios in experimental and natural sample ferromagnesian minerals (clinopyroxene, olivine and biotite), constrain magma redox at the NNO buffer, or 0.5 log units above it (NNO + 0.5). Hence, our model runs at NNO and NNO + 0.75 are expected to cover the full redox spectrum of CF deep-feeding melts, although three runs at more oxidized (NNO + 1.5) conditions have also been performed to explore model sensitivity to changing redox (Supplementary Data 1). It is important to consider that our runs are conducted in isothermal conditions (T = 1,120 °C; estimated using rhyolite-MELTS71) and with no crystallization allowed, and as such are representative of (closed system) decompressional degassing of a trachybasalt, with no attempt to reproduce more evolved magma compositions (trachytic to phonolitic). These more felsic magmas are known to be systematically poor in both sulfur (Extended Data Fig. 3b) and CO2 (ref. 72), and considering the intense CO2 discharge at CF (from both fumaroles73,74 and diffuse degassing structures58), are unlikely sources of volatiles for the ongoing unrest.
Results of model calculations (Fig. 5 and Extended Data Fig. 3) indicate that sulfur release from CF trachybasalts starts relatively deep during the magma decompressional (ascent) path. Especially in more reduced conditions, roughly half (NNO + 0.75) or more (NNO) of the initial sulfur cargo is lost from melt (and partitioned into the gas phase) in the 400–200 MPa pressure interval (∼16 to ∼8 km depth interval) (Fig. 5). This relatively deep sulfur loss to gas at CF is consistent with the large sulfur drop observed in natural samples, from trachybasaltic (SiO2 < 50 wt%) MIs (S > 1,500 ppm) to more evolved (SiO2 > 60 wt%) MIs (S < 750 ppm) (Extended Data Fig. 3). Note that shallower entrapment conditions (200–50 MPa) and hence shallower magma storage (∼8–2 km depth) have been inferred72 for such sulfur-poorer trachytic to phonolitic MIs. The model-predicted composition of the equilibrium magmatic gas (Fig. 5b–f) becomes increasingly CO2-richer with increasing pressure, but the CO2/ST versus pressure dependence is less steep than predicted by other models75, as already noted27 for other arc magma compositions. The highest modelled (molar) CO2/ST ratios (≥10) are observed at P ≥ 400 MPa in the model runs with high initial CO2 (2 wt%) (Fig. 5b). At the model run conditions, total magmatic gaseous sulfur (ST) is calculated to consist roughly of 40% SO2(g), 60% H2S(g) at NNO (and P > 100 MPa) and 85% SO2(g), 15% H2S(g) at NNO + 0.75 (and P > 100 MPa) (Fig. 5c). SO2(g) is by far the dominant sulfur species at surface conditions (0.1 MPa pressure), as typically found in erupting and/or open-vent volcanoes76.
The isotopic composition of total magmatic gaseous sulfur (\({{{\updelta }}}^{34}{{\rm{S}}}_{{{\rm{S}}}_{{\rm{T}}}}\)), illustrated in Fig. 3a and Fig. 6, is calculated as59:
where δ34Si is fixed at –1.7‰ based on our MI results (Fig. 6), F is the residual fraction of sulfur remaining in the melt at each decompression step (derived from the degassing model27) and α is the gas–melt equilibrium sulfur isotope fractionation factor (calculated from equation 39 in ref. 59). As defined59, the derived α values account for both the sulfur speciation in melt and gas (in our case, calculated from the degassing model27) and the relevant fractionation factors between all oxidized/reduced sulfur couples. All calculated α values are >1. All calculations, summarized in Supplementary Data 1, are made assuming closed-system equilibrium conditions. Results (Figs. 3a and 6) indicate modelled \({{{\updelta }}}^{34}{{\rm{S}}}_{{{\rm{S}}}_{{\rm{T}}}}\) values ranging from –3.7‰ to –1.7‰. More positive \({{{\updelta }}}^{34}{{\rm{S}}}_{{{\rm{S}}}_{{\rm{T}}}}\) compositions (up to ∼+8‰) are obtained at low pressure if open-system degassing conditions are assumed (see Supplementary Data 1).
Data availability
Source data are provided with this paper. All other data generated or analysed in this study are provided in Supplementary Tables 1 and 2, in Supplementary Data 1 and via figshare (https://doi.org/10.6084/m9.figshare.25794447)77.
References
Branney, M. & Acocella, V. in The Encyclopedia of Volcanoes 299–315 (eds. Sigurdsson, H. et al.) (Elsevier, 2015).
Druitt, T. H. & Sparks, R. S. J. On the formation of calderas during ignimbrite eruptions. Nature 310, 679–681 (1984).
Orsi, G., De Vita, S. & Di Vito, M. The restless, resurgent Campi Flegrei nested caldera (Italy): constraints on its evolution and configuration. Geotherm. Res. 74, 179–214 (1996).
Lowenstern, J. B. & Hurwitz, S. Monitoring a supervolcano in repose: heat and volatile flux at the Yellostone caldera. Elements 4, 35–40 (2008).
Newhall, C. G. & Dzurisin, D. Historical Unrest at Large Calderas of the World (USGS, 1988).
Acocella, V., Di Lorenzo, R., Newhall, C. & Scandone, R. An overview of recent (1988-2014) caldera unrest: knowledge and perspectives. Revs. Geophys. 53, 896–955 (2015).
Wicks, C. W., Thatcher, W., Dzurisin, D. & Svarc, J. Uplift, thermal unrest and magma intrusion at Yellowstone caldera. Nature 440, 72–75 (2006).
Hill, D. P. in Mechanisms of Activity and Unrest at Large Calderas Vol. 269 (eds. Troise, C. et al.) 171–187 (Geological Society of London, 2006).
Dzurisin, D., Savage, J. C. & Fournier, R. O. Recent crustal subsidence at Yellowstone caldera, Wyoming. Bull. Volcanol. 52, 247–270 (1990).
Gottsmann, J. et al. Oscillations in hydrothermal systems as a source of periodic unrest at caldera volcanoes: multiparameter insights from Nisyros, Greece. Geophys. Res. Lett. https://doi.org/10.1029/2007GL029594 (2007).
Di Vito, M. A. et al. Magma transfer at Campi Flegrei caldera (Italy) before the 1538 AD eruption. Sci. Rep. https://doi.org/10.1038/srep32245 (2016).
Scarpa, R. et al. in Campi Flegrei, Active Volcanoes of the World Series (eds. Orsi, G. et al.) 257–282 (Springer, 2022).
Kilburn, C. R. J., De Natale, G. & Carlino, S. Progressive approach to eruption at Campi Flegrei caldera in southern Italy. Nat. Commun. https://doi.org/10.1038/ncomms15312 (2017).
Kilburn, C. R. J., Carlino, S., Danesi, S. & Pino, N. A. Potential for rupture before eruption at Campi Flegrei caldera, Southern Italy. Commun. Earth Environ. https://doi.org/10.1038/s43247-023-00842-1 (2023).
Chiodini, G. et al. in Campi Flegrei, Active Volcanoes of the World Series (eds. Orsi, G. et al.) 239–256 (Springer, 2022).
Chiodini, G. et al. Magmas near the critical degassing pressure drive volcanic unrest towards a critical state. Nat. Commun. https://doi.org/10.1038/ncomms13712 (2016).
D’Auria, L. et al. Magma injection beneath the urban area of Naples: a new mechanism for the 2012–2013 volcanic unrest at Campi Flegrei caldera. Sci. Rep. https://doi.org/10.1038/srep13100 (2015).
Moretti, R., Troise, C., Sarno, F. & De Natale, G. Caldera unrest driven by CO2-induced drying of the deep hydrothermal system. Sci. Rep. https://doi.org/10.1038/s41598-018-26610-2 (2018).
Troise, C., De Natale, G., Schiavone, R., Somma, R. & Moretti, R. The Campi Flegrei caldera unrest: discriminating magma intrusions from hydrothermal effects and implications for possible evolution. Earth Sci. Rev. 188, 108–122 (2019).
Farrar, C. D. et al. Forest-killing diffuse CO2 emission at Mammoth Mountain as a sign of magmatic unrest. Nature 376, 675–678 (1995).
Sorey, M. L. et al. Carbon dioxide and helium emissions from a reservoir of magmatic gas beneath Mammoth Mountain, California. J. Geophys. Res. Solid Earth 103, 15303–15323 (1998).
Chiodini, G. et al. Magma degassing as a trigger of bradyseismic events: the case of Phlegrean Fields (Italy). Geophys. Res. Lett. https://doi.org/10.1029/2002GL016790 (2003).
Lowenstern, J. B., Smith, R. B. & Hill, D. P. Monitoring super-volcanoes: geophysical and geochemical signals at Yellowstone and other large caldera systems. Phil. Trans. R. Soc. A 364, 2055–2072 (2006).
Chiodini, G. et al. Insights from fumarole gas geochemistry on the origin of hydrothermal fluids on the Yellowstone Plateau. Geochim. Cosmochim. Acta 89, 265–278 (2012).
Caliro, S., Chiodini, G. & Paonita, A. Geochemical evidences of magma dynamics at Campi Flegrei (Italy). Geochim. Cosmochim. Acta 132, 1–15 (2014).
Edmonds, M. & Wallace, P. J. in Elements Vol. 13 (eds. Putirka, K. D. & Cooper, K. M.), 29–34 (Mineralogical Society of America, 2017).
Ding, S., Plank, T., Wallace, P. J. & Rasmussen, D. J. Sulfur_X: a model of sulfur degassing during magma ascent. Geochem. Geophysi. Geosyst. https://doi.org/10.1029/2022GC010552 (2023).
Wallace, P. J. & Edmonds, M. The sulfur budget in magmas: evidence from melt inclusions, submarine glasses, and volcanic gas emissions. Rev. Mineral. Geochem. 73, 215–246 (2011).
Henley, R. W. et al. Porphyry copper deposit formation by sub-volcanic sulphur dioxide flux and chemisorption. Nat. Geosci. 8, 210–215 (2015).
Giggenbach, W. F. Geothermal gas equilibria. Geochim. Cosmochim. Acta 44, 2021–2032 (1980).
Giggenbach, W. F. Redox processes governing the chemistry of fumarolic gas discharges from White Island, New Zealand. Appl. Geochem. 2, 143–161 (1987).
Chiodini, G. et al. Hydrothermal pressure–temperature control on CO2 emissions and seismicity at Campi Flegrei (Italy). J. Volcanol. Geotherm. Res. https://doi.org/10.1016/j.jvolgeores.2021.107245 (2021).
Allard, P., Maiorani, A., Tedesco, C., Cortecci, D. & Turi, B. Isotopic study of the origin of sulfur and carbon in Solfatara fumaroles, Campi Flegrei caldera. J. Volcanol. Geotherm. Res. 48, 139–159 (1991).
Hedenquist, J. W. & Lowenstern, J. B. The role of magmas in the formation of hydrothermal ore deposits. Nature 370, 519–527 (1994).
Henley, R. W. & Fischer, T. P. Sulfur sequestration and redox equilibria in volcanic gases. J. Volcanol. Geotherm. Res. https://doi.org/10.1016/j.jvolgeores.2021.107181 (2021).
Piochi, M. et al. Native sulfur, sulfates and sulfides from the active Campi Flegrei volcano (southern Italy): genetic environments and degassing dynamics revealed by mineralogy and isotope geochemistry. J. Volcanol. Geotherm. Res. 304, 180–193 (2015).
Mangiacapra, A. et al. The deep magmatic system of the Campi Flegrei caldera (Italy). Geophys. Res. Lett. https://doi.org/10.1029/2008GL035550 (2008).
Zollo, A. et al. Seismic reflections reveal a massive melt layer feeding Campi Flegrei caldera. Geophys. Res. Lett. https://doi.org/10.1029/2008GL034242 (2008).
Buono, G. et al. New insights Into the recent magma dynamics under Campi Flegrei caldera (Italy) from petrological and geochemical evidence. J. Geophys. Res. Solid Earth https://doi.org/10.1029/2021JB023773 (2022).
Labidi, J., Cartigny, P., Birck, J. L., Assayag, N. & Bourrand, J. J. Determination of multiple sulfur isotopes in glasses: a reappraisal of the MORB δ34S. Chem. Geol. 334, 189–198 (2012).
Muth, M. J. & Wallace, P. J. Slab-derived sulfate generates oxidized basaltic magmas in the southern Cascade arc (California, USA). Geology 49, 1177–1181 (2021).
Taracsák, Z. et al. Sulfur from the subducted slab dominates the sulfur budget of the mantle wedge under volcanic arcs. Earth Planet. Science Lett. https://doi.org/10.1016/j.epsl.2022.117948 (2023).
Astort, A. et al. Tracking the 2007–2023 magma-driven unrest at Campi Flegrei caldera (Italy). Commun. Earth Environ. https://doi.org/10.1038/s43247-024-01665-4 (2024).
Giacomuzzi, G., Chiarabba, C., Bianco, F., De Gori, P. & Agostinetti, N. P. Tracking transient changes in the plumbing system at Campi Flegrei Caldera. Earth Planet. Sci. Lett. https://doi.org/10.1016/j.epsl.2024.118744 (2024).
Lima, A. et al. Thermodynamic model for uplift and deflation episodes (bradyseism) associated with magmatic–hydrothermal activity at the Campi Flegrei (Italy). Earth Sci. Rev. 97, 44–58 (2009).
Costa, F., Shea, T. & Ubide, T. Diffusion chronometry and the timescales of magmatic processes. Nat. Rev. Earth Environ. 1, 201–214 (2020).
Parks, M. M. et al. Evolution of Santorini Volcano dominated by episodic and rapid fluxes of melt from depth. Nat. Geosci. 5, 749–754 (2012).
Druitt, T. H., Costa, F., Deloule, E., Dungan, M. & Scaillet, B. Decadal to monthly timescales of magma transfer and reservoir growth at a caldera volcano. Nature 482, 77–80 (2012).
Guidoboni, E. & Ciuccarelli, C. The Campi Flegrei caldera: historical revision and new data on seismic crises, bradyseisms, the Monte Nuovo eruption and ensuing earthquakes (twelfth century 1582 AD). Bull. Volcanol. 73, 655–677 (2011).
Rosi, M. et al. Defining the pre-eruptive states of active volcanoes for improving eruption forecasting. Front. Earth Sci. https://doi.org/10.3389/feart.2022.795700 (2022).
Giggenbach, W. F. & Gouguel, R. L. Collection and Analysis of Geothermal Volcanic Water and Gas Discharges (DSIR, 1989).
Caliro, S. et al. The origin of the fumaroles of La Solfatara (Campi Flegrei, South Italy). Geochim. Cosmochim. Acta https://doi.org/10.1016/j.gca.2007.04.007 (2007).
Christenson, B. W. et al. Cyclic processes and factors leading to phreatic eruption events: insights from the 25 September 2007 eruption through Ruapehu Crater Lake, New Zealand. J. Volcanol. Geotherm. Res. https://doi.org/10.1016/j.jvolgeores.2010.01.008 (2010).
Stix, J. & de Moor, J. M. Understanding and forecasting phreatic eruptions driven by magmatic degassing. Earth Planets Space https://doi.org/10.1186/s40623-018-0855-z (2018).
Rosi, M. & Sbrana, A. Phlegrean Fields. Quad. Ric. Sci. 9, 187 (1987).
Mormone, A. et al. Secondary hydrothermal minerals in buried rocks at the Campi Flegrei caldera, Italy: a possible tool to understand the rock-physics and to assess the state of the volcanic system. Period. Mineral. https://doi.org/10.2451/2011PM0027 (2011).
Chiodini, G., Cioni, R. & Marini, L. Reactions governing the chemistry of crater fumaroles from Vulcano Island, Italy, and implications for volcanic surveillance. Appl. Geochem. https://doi.org/10.1016/0883-2927(93)90004-Z (1993).
Cardellini, C. et al. Monitoring diffuse volcanic degassing during volcanic unrests: the case of Campi Flegrei (Italy). Sci. Rep. https://doi.org/10.1038/s41598-017-06941-2 (2017).
Marini, L., Moretti, R. & Accornero, M. Sulfur isotopes in magmatic-hydrothermal systems, melts, and magmas. Rev. Mineral. Geochem. https://doi.org/10.2138/rmg.2011.73.14 (2011).
D’Amore, F. & Panichi, C. Evaluation of deep temperatures of hydrothermal systems by a new gas geothermometer. Geochim. Cosmochim. Acta 44, 549–556 (1980).
Chiodini, G. & Marini, L. Hydrothermal gas equilibria: the H2O–H2–CO2–CO–CH4 system. Geochim. Cosmochim. Acta https://doi.org/10.1016/S0016-7037(98)00181-1 (1998).
Marini, L., Principe, C. & Lelli, M. Revised conceptual model of the Solfatara magmatic–hydrothermal system (Campi Flegrei, Italy), time changes during the last 40 years, and prediction of future scenarios. Preprint at EGUsphere https://doi.org/10.5194/egusphere-2024-1306 (2024).
Iacono-Marziano, G., Morizet, Y., Le Trong, E. & Gaillard, F. New experimental data and semi-empirical parameterization of H2O–CO2 solubility in mafic melts. Geochim. Cosmochim. Acta 97, 1–23 (2012).
Mormone, A. et al. A CO2-rich magma source beneath the Phlegraean Volcanic District (Southern Italy): evidence from a melt inclusion study. Chem. Geol. https://doi.org/10.1016/j.chemgeo.2011.05.019 (2011).
Esposito, R. et al. Magmatic evolution of the Campi Flegrei and Procida volcanic fields, Italy, based on interpretation of data from well-constrained melt inclusions. Earth Sci. Rev. 185, 325–356 (2018).
Rasmussen, D. J., Plank, T. A., Wallace, P. J., Newcombe, M. E. & Lowenstern, J. B. Vapor-bubble growth in olivine-hosted melt inclusions. Am. Mineral. https://doi.org/10.2138/am-2020-7377 (2020).
Moretti, R. & Neuville, D. R. Magma Redox Geochemistry (AGU, 2021).
Hughes, E. C., Saper, L. M., Liggins, P., O’Neill, H. S. C. & Stolper, E. M. The sulfur solubility minimum and maximum in silicate melt. J. Geol. Soc. https://doi.org/10.1144/jgs2021-125 (2023).
Oppenheimer, C., Fischer, T. P. & Scaillet, B. in Treatise on Geochemistry 2nd edn (eds Holland, H. D. & Turekian, K. K.) 111–179 (Elsevier, 2014).
Bardeglinu, I. Pre-eruptive Magma Conditions at Campi Flegrei (italy): An Experimental Petrology Study. PhD thesis, Univ. d’Orléans and Univ. PisaFirenze (2020).
Ghiorso, M. S. & Gualda, G. A. R. An H2O–CO2 mixed fluid saturation model compatible with rhyolite-MELTS. Contrib. Mineral. Petrol. https://doi.org/10.1007/s00410-015-1141-8 (2015).
Arienzo, I., Moretti, R., Civetta, L., Orsi, G. & Papale, P. The feeding system of Agnano–Monte Spina eruption (Campi Flegrei, Italy): dragging the past into present activity and future scenarios. Chem. Geol. https://doi.org/10.1016/j.chemgeo.2009.11.012 (2010).
Aiuppa, A. et al. First observations of the fumarolic gas output from a restless caldera: implications for the current period of unrest (2005–2013) at Campi Flegrei. Geochem. Geophys. Geosyst. https://doi.org/10.1002/ggge.20261 (2013).
Tamburello, G. et al. Escalating CO2 degassing at the Pisciarelli fumarolic system, and implications for the ongoing Campi Flegrei unrest. J. Volcanol. Geotherm. Res. https://doi.org/10.1016/j.jvolgeores.2019.07.005 (2019).
Moretti, R., Papale, P. & Ottonello, G. A model for the saturation of C–O–H–S fluids in silicate melts. Geol. Soc. Spec. Publ. https://doi.org/10.1144/GSL.SP.2003.213.01.06 (2003).
Aiuppa, A., Fischer, T. P., Plank, T., Robidoux, P. & Di Napoli, R. Along-arc, inter-arc and arc-to-arc variations in volcanic gas CO2/ST ratios reveal dual source of carbon in arc volcanism. Earth Sci. Rev. 168, 24–47 (2017).
Caliro, S. et al. Data for 'Escalation of caldera unrest indicated by increasing emission of isotopically light sulfur'. figshare https://doi.org/10.6084/m9.figshare.25794447 (2024).
Tarquini, S. et al. Release of a 10-m-resolution DEM for the Italian territory: comparison with global-coverage DEMs and anaglyph-mode exploration via the web. Comput. Geosci. 38, 168–170 (2012).
Cannatelli, C. et al. Geochemistry of melt inclusions from the Fondo Riccio and Minopoli 1 eruptions at Campi Flegrei (Italy). Chem. Geol. https://doi.org/10.1016/j.chemgeo.2006.07.012 (2007).
Arienzo, I., Mazzeo, F. C., Moretti, R., Cavallo, A. & D’Antonio, M. Open-system magma evolution and fluid transfer at Campi Flegrei caldera (southern Italy) during the past 5 ka as revealed by geochemical and isotopic data: the example of the Nisida eruption. Chem. Geol. 427, 109–124 (2016).
Cioni, R. et al. in Volcanic Hazard (ed. Latter, J. H.) 384–398 (Springer, 1989).
Dall’Aglio, M., Martini, M. & Tonani, F. Rilevamento geochimico delle emissioni vulcaniche dei Campi Flegrei. Quaderni de “La Ricerca Scientifica”, 83 (1972).
Acknowledgements
This work was funded by the Italian Presidenza del Consiglio dei Ministri—Dipartimento della Protezione Civile (DPC), but does not necessarily represent DPC official opinion and policies (S.C. and M.A.D.V.). The authors also received funding from the INGV research project LOVE-CF (Linking Surface Observables to Subvolcanic Plumbing-Aystem: A Multidisciplinary Approach for Eruption Forecasting at Campi Flegrei Caldera, Italy) (L.P.) and from the European Union Next-GenerationEU (National Recovery and Resilience Plan—NRRP, Mission 4, Component 2, Investment 1.3–D.D. 1243 2/8/2022, PE0000005) under the RETURN Extended Partnership (A.A.).
Author information
Authors and Affiliations
Contributions
S.C., G.C. and A.A. devised the study concept. R.A., A.C., E.C., M.A.D.V., C.M., F.R., A.S., J.L., A.M., B.M., L.P., Z.T., C.T. and S.V. contributed to refinement of the initial concept and to data collection, analysis and interpretation. A.A. drafted the original version of the manuscript with contributions of S.C., G.C., L.P., Z.T., C.T. and S.V. All coauthors contributed to editing the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Geoscience thanks Bruno Scaillet, Yuri Taran and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editor: Stefan Lachowycz, in collaboration with the Nature Geoscience team.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
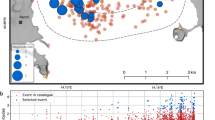
Extended Data Fig. 1 The CF caldera.
The map is based on a digital elevation model78, and illustrates epicenters of post 2018 earthquakes (https://www.ov.ingv.it/index.php/monitoraggio-e-infrastrutture/bollettini-tutti/bollett-mensili-cf), main structures (faults and caldera rims) and the center of the current maximum uplift.
Extended Data Fig. 2 Hydrothermal gas equilibria.
(a) Measured (Supplementary Table 1) vs. modelled (see Methods) gas H2S/H2O ratio. Temperature (x-axis) is the equilibrium temperature estimated from the CO-CO2 equilibrium (Eq. 8; see Methods). The model lines illustrate the pressure dependencies of H2S/H2O ratios for H2S fugacity controlled by equilibrium with either pyrite (Eq. 7), native sulphur (Eq. 13) or anhydrite (Eq. 14). In all cases, H2O fugacity is controlled by liquid-vapor coexistence (Eq. 9). (b) Temporal evolution of measured (Supplementary Table 1) and modelled (Eqs. 10, 11 and 13) H2S/CO2 ratios. Pyrite breakdown (Eq. 6) is the dominant control of fumarolic H2S in the 2003-2017 phase, but cannot explain the excess H2S observed during accelerating unrest (1982-84 and post-2018). Native sulphur is in disequilibrium conditions with fumarole composition (at CF hydrothermal T and redox conditions), and therefore will be remobilised to the gas phase if new mineral surfaces are exposed to the gas stream during escalating seismicity (and opening on few cracks/fractures and/or gas migration paths).
Extended Data Fig. 3 The composition of CF melt inclusions (MIs), compiled from the literature.
a, The trachybasaltic MIs entrapped in crystals from the Minopoli and Fondo Riccio eruptions (studied here for sulphur content and sulphur isotope composition; Supplementary Table 2) are the most mafic volcanic products ever measured37,65,79,80 at CF, and hence the most representative of the deep parental melts. In (b) the model predicted evolution of dissolved melt H2O and S contents (data from model runs 1-10 in Supplementary Data 1) are shown for comparison, and nicely reproduce the sulphur (and H2O) loss from melt (to the vapor phase) upon decompressional degassing to ~3-6 km (the storage zone of more evolved – trachytic to phonolitic – and volatile-poor melts39).
Extended Data Fig. 4 Chronogram of fumarole composition evolution at CF during 1923 to 2023.
(a) H2S concentrations; (b) H2S/CO2 ratios. The excess H2S during 2018-present is unprecedented in the recent (last century) CF degassing history. Data from: 1983-2023 (this study, Supplementary Table 1, and ref. 33); 1980-81 (FC fumarole, ref. 81); 1970 (ref. 82); 1923 (composition reported in ref. 82).
Supplementary information
Supplementary Information
Supplementary Discussion and References.
Supplementary Table 1
Dataset: Bocca Grande (BG) fumarole composition. Supplementary Table 2 Composition of melt inclusions (major elements, S and C concentrations) and host crystals from CF Fondo Riccio and Minopoli2 eruptions.
Supplementary Data 1
Input parameters and results of degassing model simulations.
Source data
Source Data Fig. 1
Statistical source data.
Source Data Fig. 2
Statistical source data.
Source Data Fig. 3
Statistical source data.
Source Data Fig. 4
Statistical source data.
Source Data Fig. 5
Statistical source data.
Source Data Fig. 6
Statistical source data.
Source Data Extended Data Fig. 1
Statistical source data.
Source Data Extended Data Fig. 2
Statistical source data.
Source Data Extended Data Fig. 3
Statistical source data.
Source Data Extended Data Fig. 4
Statistical source data.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Caliro, S., Chiodini, G., Avino, R. et al. Escalation of caldera unrest indicated by increasing emission of isotopically light sulfur. Nat. Geosci. 18, 167–174 (2025). https://doi.org/10.1038/s41561-024-01632-w
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41561-024-01632-w
This article is cited by
-
Turbulent diffusion and volcanic gas dispersion in the atmospheric surface layer: insights from La Solfatara, Campi Flegrei, Italy
Earth, Planets and Space (2025)
-
Magma chamber failure and dyke injection threshold for magma-driven unrest at Campi Flegrei caldera
Nature Communications (2025)
-
Coupled earthquakes and resonance processes during the uplift of Campi Flegrei caldera
Communications Earth & Environment (2025)
-
Deciphering unrest at Campi Flegrei
Nature Geoscience (2025)