Main

In an equilibrium climate state, iceberg calving from ice shelves is a natural process that balances mass gain from glacial inflow. In the era of climate change, Antarctic ice shelves are suffering major mass losses due to melting and calving1,2,3, thus reducing their vital ability to buttress Antarctic Ice Sheet outflow4,5. Over the past three decades, multiple small-to-medium ice shelves have experienced large-scale calving events that removed ≥10% of their areas over periods of just days to weeks6,7,8,9,10. Prominent calving events around the Antarctic Peninsula led to ice-shelf disintegrations6,7,11 that are probably connected with severe previous warming of the region12,13 and associated sea-ice loss11. As warmer temperatures spread around the Antarctic coastline, there is an urgent need to understand the wider vulnerability of ice shelves to sea-ice loss11,14 to reduce the substantial uncertainties in sea-level projections15.

Massom et al.11 connected the Antarctic Peninsula disintegration events with regional sea-ice losses, as sea ice attenuates swell16,17 and (land)fast ice provides backstress that bolsters ice shelves9,10,11,18. They proposed that, without an effective sea-ice barrier, energetic swell repeatedly flexed the damaged outer shelf margins, amplifying fractures until they calved. Sea-ice losses and swell flexure have since been implicated in calving events across Antarctica9,19,20,21, but there are few direct measurements of ice-shelf flexure22,23,24 and no model assessments of pre-calving flexure have been performed to empower predictions of future events.

In this Article, we present time series of flexural stress experienced by the Voyeykov and Wilkins ice shelves that advance our understanding of their large-scale calving events in 2007 and 2008, respectively (Fig. 1). To achieve this, we analyse satellite data from September 2002–August 2009 to quantify the pack- and fast-ice barriers25,26 and model attenuation of the incoming swell27,28 and the flexural stress imposed on the shelf fronts29,30. On the basis of our findings, we propose a conceptual model of the prolonged amplifications in flexure that precondition large-scale calving of weakened shelf fronts, and relate the model to other ice shelves (see Fig. 5).

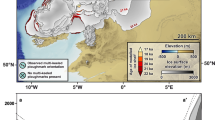
Fig. 1: Large-scale calving of the Wilkins and Voyeykov ice shelves.
figure 1

a, Map of Antarctica showing the locations of the studied ice shelves, including ice shelves used only for the results in Fig. 5b (shaded red). b–e, Environmental Satellite (ENVISAT) Advanced Synthetic Aperture Radar (ASAR) Wide Swath Medium Resolution (WSM) imagery of the Wilkins Ice Shelf (b,c, indicated by the yellow box in a) and Voyeykov Ice Shelf (d,e, indicated by the purple box in a) before (b,d) and after (c,e) the large-scale calving events. The islands dividing the Wilkins shelf front are labelled: Rothschild Island (R), Charcot Island (C) and Lataday Island (L). Areas lost to calving are indicated (green shading for Wilkins RC, orange for Wilkins CL and purple for Voyeykov). f, Timeline of the lead-ups to the large-scale calving events, colour coded according to the shelf front.

Full size image

Exposure of damaged outer shelf margins to swell

The eastern section of the Voyeykov Ice Shelf was heavily fractured over the duration of analysed satellite images (from September 2002). The fractures propagated towards the shelf front before it calved in late April 2007 (Fig. 2a–c) in an event that removed 14% of its area over 4–5 days (ref. 9). The Wilkins shelf front is divided into distinct sections by islands (Rothschild Island, Charcot Island and Latady Island; Fig. 1b,c). The two fronts investigated are referred to as the Wilkins RC (Fig. 2d–f) and Wilkins CL (Fig. 2g–i), according to the bounding islands. The Wilkins RC suffered a large calving event in 19987,31, but many icebergs subsequently refroze to the shelf front in a mélange layer32, which supported the heavily damaged shelf-front region. In contrast, the Wilkins CL existed along an ice bridge with only one major fracture for the majority of the analysed period (Fig. 2g–i, gold curve). A 52-km-long fracture formed closer to the Wilkins CL front in July 2007 (Fig. 2i, purple curve)7,33, along which it calved in late February 2008 and then along the previous fracture in late May 2008, removing a combined area of 650 km2. The Wilkins RC then calved in late June 2008, with an area of 1,480 km2 lost over two weeks. In total, the calving events removed 17% of the Wilkins31. The Bedmap2 dataset34 implies that both ice shelves were <100 m thick in the areas that calved, indicating that swell has the potential to dominate ice-shelf stress35,36.

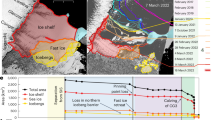
Fig. 2: Sea-ice and shelf-front conditions in the years before large-scale calving events.
figure 2

a–i, Sea-ice types and ice-shelf damage superimposed on ENVISAT ASAR WSM imagery from daily Advanced Microwave Scanning Radiometer for EOS (AMSR-E) ARTIST sea-ice (ASI) dataset and fast-ice extent from ref. 25 (Methods) for the Voyeykov (a–c), Wilkins RC (d–f) and Wilkins CL (g–i). The images are oriented so that the relevant shelf front points upwards. For each shelf front, the images shown were taken at similar periods before the respective calving events: in the low sea-ice year 2004 (a,d,g), the year before (b,e,h) and dates less than 2 weeks before (c,f,i). Fractures are superimposed on the ice shelves (thin black curves), with two Wilkins CL fractures along which calving occurred highlighted (thick gold and purple curves).

Full size image

Over the 7-year record, each shelf front was typically protected by an inner fast-ice barrier extending tens of kilometres from the shelf front, followed by an outer pack-ice barrier extending tens to hundreds of kilometres. Before the calving events, perennial fast ice made up nearly all of the Voyeykov fast-ice barrier (Fig. 2a,b) and a major proportion of the Wilkins RC fast-ice barrier (Fig. 2d,e). The perennial fast-ice barriers for the Voyeykov and Wilkins RC persisted even in periods with relatively low sea-ice extents, such as around the Wilkins in summer 2004 (Figs. 2g and 3f). Annual fast ice constitutes almost all of the Wilkins CL fast-ice barrier (Fig. 2h). During late summer 2004, the Wilkins CL lost its fast-ice barrier for 5 months, in addition to losing the majority of its pack-ice barrier, creating a wide corridor for ocean swell to reach the shelf front (Fig. 2g). This was the longest duration of exposure of the Wilkins CL to the open ocean over the analysed record before the calving event (compare the numbers of low sea-ice days in Fig. 3c).

Fig. 3: Sea-ice lengths over 2003–2009.
figure 3

a–c, Yearly count of low sea-ice days (Lpck ≤ 50 km, Ltot ≤ 100 km) for the Voyeykov (a), Wilkins RC (b) and Wilkins CL (c) (years are September–August). d–i, Daily time-series of effective sea-ice lengths for Lpck (d,f,h) and Lann and Lper (e,g,i) for the Voyeykov (d,e), Wilkins RC (f,g) and Wilkins CL (h,i). The sea-ice lengths shown are means for the lowest 33% of transects for a particular shelf front on a given day (Methods). The lighter shaded regions are after the calving events (the second calving event for the Wilkins CL).

Full size image

In the months leading up to the calving events, each of the three shelf fronts experienced increasing exposure to the open ocean through reduced or diminished sea-ice barriers. Four months before the Voyeykov calving, its pack-ice and annual fast-ice barriers retreated rapidly due to cyclonic conditions and strong katabatic winds9, and in late March 2007 the perennial fast ice attached the eastern side of the shelf front broke-up (Figs. 2c and 3d,e). In the lead-up to the Wilkins calving events, the formation of La Niña and a persistent deep Admundsen Sea low drove surrounding sea-ice loss37,38,39,40. Thus, the Wilkins CL had no fast-ice barrier and the least pack ice since 2004 in the 2 weeks before its first calving event (Fig. 2i; compare with Fig. 3h)11. The Wilkins RC perennial fast ice survived the initial pack-ice loss, but the record high temperatures during early winter 200839 compounded the initial loss of the pack-ice and annual fast-ice barriers, such that the perennial fast-ice layer eventually broke away from the shelf front (Fig. 2f).

Prolonged reductions in sea-ice barriers

Over the record, each shelf front experiences the greatest number of days with a total effective sea-ice length Ltot ≡ Lpck + Lann + Lper ≤ 100 km (where Lpck is the effective pack-ice length, Lann is the annual fast-ice length and Lper is the perennial pack-ice length; a value of Ltot > 100 km reduces the height of a 12 s swell by >90%) combined with a high number of days with Lpck ≤ 50 km (the e-folding length for a 12 s swell) in the years of the calving events (years are September–August; Fig. 3a–c). For the Voyeykov, the large number of low sea-ice days in 2007 is caused by a sharp drop in (effective) pack-ice length (Fig. 3d) starting in November 2006 (<6 months before calving) and a drop in annual fast-ice length (Fig. 3e) starting shortly afterwards. The perennial fast ice attached to the eastern shelf front collapses about 3 months later (<1 month before calving; Fig. 3e). The Wilkins RC experiences a weaker version of the sequence in the year before calving (starting <18 months before calving), which probably preconditioned extreme sea-ice losses in 2008, alongside supportive atmospheric conditions in winter 2007 to early 200839, which contrast with conditions that favoured sea-ice recovery in 200541. The extreme sea-ice loss in 2008 includes the shortest perennial fast-ice lengths over the record before calving, with Lper < 1 km on some days in April 2008, compared with (for example) Lper > 5 km in 2004 (Fig. 3g). There is also evidence of preconditioning in the year before calving for the Wilkins CL, starting (<18 months before the calving events) with the onset of a rapid decrease in pack-ice length from the end of December 2006 to mid-January 2007 and the subsequent removal of fast ice from March–June 2007 (Fig. 3h–l). Pack ice and annual fast ice return partially during winter 2007 (compared with previous years), such that the pack ice retreats early (starting December 2007, <6 months before the calving events) and rapidly, followed by fast-ice removal in January 2008, which does not recover until after the calving events.

Sustained durations of swell-induced flexure

The model predicts major increases in the number of days for which swell-induced flexural stress is estimated to exceed internal stress (≥30 kPa) and be comparable to it (10–30 kPa)36 in the calving year and the year before (Fig. 4a–c), and noting that the model does not incorporate additional stress due to damage. The underlying daily time series is given for 60-day accumulated stress (Fig. 4d–f) to represent the importance of ice-shelf fatigue created by sustained swell impacts11,42,43,44. For each shelf front, the yearly peaks (following summer and the sea-ice minima) are anomalously large and wide in both the year of the calving events and the year before. For the Voyeykov (Fig. 4d), the interannual variability from 2003–2006 is driven by incoming swell (black and purple curves are similar), including the largest overall peak in summer 2006 (<18 months before calving). In late 2006 (<6 months before calving), the 60-day accumulated stress normalized by the average yearly maximum (\({\hat{\sigma }}_{60}\)) is >1 (that is, the accumulated stress is greater than its average yearly maximum) due to a rapid retreat of sea-ice length (black curve above purple), which lasts until mid-March 2007. In 2007, the Wilkins RC has \({\hat{\sigma }}_{60} > 1\) for approximately 2 weeks, whereas Wilkins CL has \({\hat{\sigma }}_{60} > 1\) for ~2 months (both <18 months before calving; Fig. 4e,f). Following an early sea-ice retreat, Wilkins RC has \({\hat{\sigma }}_{60} > 1\) from January to mid-February 2008 (<6 months before calving), and then again from April until after the calving event, with a maximum of \({\hat{\sigma }}_{60} > 2\) in early May. The Wilkins CL has rapidly increasing accumulated stress at the beginning of 2008 (<6 months before the first calving), reaching \({\hat{\sigma }}_{60}\approx 0.7\) during February 2008 (<1 month before the first calving) and then increasing to \({\hat{\sigma }}_{60}\approx 1.7\) at the second calving event.

Fig. 4: Flexural ice-shelf stress due to swell over 2003–2009.
figure 4

a–c, Number of days with σ = 10–30 kPa and σ ≥ 30 kPa for the Voyeykov (a), Wilkins RC (b) and Wilkins CL (c). d–f, Daily time-series of 60-day accumulated stress values normalized by the average yearly maxima using daily sea-ice lengths (Fig. 3d–i) and daily median wave heights (\({\hat{\sigma }}_{60}\); black curves), for the Voyeykov (d), Wilkins RC (e) and Wilkins CL (f). Time-series using climatological sea-ice lengths (daily average over the 7-year record) and daily median wave heights (\({\hat{\sigma }}_{60}^{{\rm{aice}}}\); purple curves) are included to indicate where variations are driven by swell (black and purple curves are similar) or by sea-ice lengths (black and purple curves separate). Daily time-series of total sea-ice lengths normalized by the total transect length are shown in the background (\({\hat{L}}_{{\rm{tot}}}\); shaded regions), where the transects extend to 10° N of the shelf fronts for Wilkins RC and Voyeykov, and 12° W for Wilkins CL (Methods). As in Fig. 3, the lighter shaded regions in a–f are after the calving events.

Full size image

Conceptual model and implications

The findings are distilled into a conceptual model of the swell–sea-ice–shelf-front processes leading to the sustained flexure that we propose triggered the large-scale calving events (Fig. 5a). This model advances the conceptual model presented by Massom et al.11 for the Larsen A, B and Wilkins disintegration events by emphasizing key timings, including fast ice, and separating the Wilkins RC and CL events. The processes are divided into preconditioning <18 months before calving, preconditioning <6 months before and triggering <1 month before. The conceptual model encompasses the commonalities between the Wilkins RC, CL and Voyeykov, in terms of the reduced pack ice, the removal of fast ice and the shelf-front weakening. It also accounts for key differences, such as amplified flexure being driven by pack-ice loss for the Wilkins RC and CL versus large swell for the Voyeykov (Fig. 4d–f), and the absence of long-term perennial fast ice and the formation of a large fracture for the Wilkins CL (Figs. 2i and 3i).

Fig. 5: Conceptual model of swell–sea-ice–shelf front processes leading to large-scale calving events and instantaneous stress versus ice-shelf thickness.
figure 5

a, Processes are divided into preconditioning <18 months before calving, preconditioning <6 months before and triggering <1 month before, for pack ice and swell (pink boxes), fast ice (blue) and shelf fronts (grey). b, Flexural stress created by 12 s swell and normalized by the incident amplitude, A, versus ice-shelf thickness with no sea-ice barrier (solid black line), a 100-km pack-ice barrier (dashed) and a 100-km sea-ice barrier (60 km of pack ice, 20 km of annual fast ice and 20 km of perennial fast ice; dash-dotted). The stress values for the ice shelves highlighted in Fig. 1a are overlain (without sea-ice barriers; labelled data points), including the Wilkins and Voyeykov shelf fronts (light-blue squares) and results with median sea-ice barriers in the 60-day window before calving (red squares, with red lines denoting quartiles). Other ice shelves are included, with blue data points showing cases with reported thickness values (the square data points are the mean thickness and vertical lines are thickness ranges) and green data points showing thickness values calculated using CryoSat-2 data (the square data points represent the median thickness values and the lines are the quartiles).

Full size image

Other large-scale calving events, such as McMurdo 2016 and Conger–Glenzer 2022, have been linked with sea-ice loss and swell-induced flexure19,45. They seem to fit the conceptual model, as they both involved thin ice shelves with fast ice attached to the shelf fronts, and they calved following prolonged reductions in their sea-ice barriers19,45, although preconditioning in the year before calving is unknown. Without a sea-ice barrier, a large-amplitude 12 s swell could create flexural stress comparable to internal stress in the Conger–Glenzer (σ/A ≈ 2 kPa m−1; Fig. 5b) and an amplitude of only 1 m would create flexural stress likely to exceed internal stress in the McMurdo (σ/A > 30 kPa m−1)35,36. The McMurdo 2016 event is closest to the Wilkins RC/Voyeykov version of the model, as it calved over a heavily fractured area without a fast-ice barrier19, whereas the Conger–Glenzer 2022 event has aspects of both versions of the model, including amplification of a large fracture45, as with the Wilkins CL. The Parker 2019 and Larsen B 2022 large-scale calving events have also been linked with sea-ice loss10,20, and seem to be aligned with the conceptual model, despite being considerably thicker than the Wilkins and Voyeykov (such that 0.1 < σ/A < 1 kPa m−1 without a sea-ice barrier; Fig. 5b). However, in general, the conceptual model does not apply to thicker ice shelves. For instance, there are no indications that the Larsen C 2017, Brunt 2023 or Brunt 2024 large-scale calving events are linked to sea-ice losses.

Our findings indicate that rapid and widespread Antarctic sea-ice loss will be an important factor in future large-scale calving events. Even a hypothesized extreme rate of thinning over the years studied for the Wilkins and Voyeykov has a far smaller impact on swell-induced flexure than the sea-ice losses they experienced (Extended Data Fig. 1). In terms of the instantaneous flexural stress in response to a 12 s swell, the median sea-ice barriers (2003–calving) for the Voyeykov and Wilkins RC approximately double their effective thickness (Fig. 5b). More generally, an effective sea-ice barrier (Ltot = 100 km) is equivalent to an additional 50–100 m of ice-shelf thickness (for a 12 s swell; Fig. 5b). The context of each shelf front should also be considered—for instance, the thin McMurdo exists in a sheltered location that probably protects it from frequent large swell. Moreover, swell-induced stress will be amplified in fractures not captured in the model30; note that glaciological stress was also amplified to ~200 kPa in fractures present on the Wilkins before calving33, which is comparable to the largest of our predicted stress values (for median significant wave height values and without fractures). However, the rapidly thinning and weakening Pine Island and Thwaites46,47,48 still have a long way to go before swell-induced stress becomes a likely contributor to calving, even without sea-ice barriers (σ/A on the order of 10−2 kPa m−1; Fig. 5b).

Methods

Identification of ice-shelf damage

Satellite images (Figs. 1 and 2) are ASAR WSM imagery from ENVISAT, which operated from March 2002–April 2012. Owing to its all-weather, day–night imaging capability, ENVISAT ASAR WSM imagery is available in late autumn and winter, which covers the Wilkins and Voyeykov calving events. A basemap of Antarctica, its islands and the Voyeykov and Wilkins ice shelves was imported from the Making Earth System Data Records for Use in Research Environments (MEaSUREs) Antarctic Boundaries for International Polar Years 2007–2009 from Satellite Radar (Version 2)49. We edited the Wilkins shelf fronts in the MEaSUREs Antarctic Boundaries dataset to match the ENVISAT ASAR WSM imagery. As the Voyeykov is unconfined and terminates into a widespread mélange layer, we edited its shelf-front locations in the MEaSUREs Antarctic Boundaries dataset to match those given by ref. 9. Fracture locations were identified using a method previously applied to the Voyeykov9 and the George VI50. The method uses both ENVISAT ASAR WSM and Landsat-7 Enhanced Thematic Mapper Plus images, with fractures manually mapped in Quantum Geographic Information System (QGIS). For guidance, we used similar work undertaken to map fracture locations for the Wilkins from 1990–2008, using imagery from ENVISAT ASAR, the Advanced Land Orbit satellite and Terra Advanced Spaceborne Thermal Emission and Reflection Radiometer satellites7,31.

The reported percentage changes in ice-shelf area due to calving were calculated by comparing the area of the ice shelf pre- and post-calving. This was achieved by comparing ice-shelf extents over different years using ENVISAT ASAR WSM imagery and manually drawing polygons in QGIS to represent the areas lost to calving. Extended Data Table 1 lists all ice-shelf images used in the study.

Sea-ice lengths

Reported sea-ice lengths (Fig. 3) were calculated from a combination of (1) sea-ice concentration data from the AMSR-E ASI sea-ice dataset51 and (2) fast-ice extent datasets from ref. 25. Sea-ice concentration data are given as a percentage of areal sea-ice cover per grid cell on the ocean surface at a spatial resolution of 3.125 km2 and a daily frequency from June 2002–September 2011. The fast-ice dataset is a binary measure per grid cell at a spatial resolution of 1 km2 and a 15-day frequency from March 2000–March 2018. The fast-ice dataset includes an Antarctic land mask, for which ice-shelf extents are updated every March25. For consistency, we changed the Voyeykov shelf front in the fast-ice dataset to that given by ref. 9, and we updated the Wilkins land mask at each calving event in 2008. To pair the sea-ice and fast-ice datasets, we converted the fast-ice dataset to a 3.125 km2 resolution (to match the AMSR-E grid). AMSR-E sea-ice outputs were imported into QGIS, which produced the sea-ice maps in Fig. 2, where the pack-ice boundaries are corrected for fast ice from the converted fast-ice dataset25.

An algorithm to calculate the presence and age of fast ice and the location of the shelf fronts was applied to the sea-ice and fast-ice datasets on the 3.125 km2 grid. For each shelf front:

  1. (i)

    On the first day of the fast-ice record (1 September 2000), a counter was initiated to track the number of continuous days fast ice is present in each grid cell.

  2. (ii)

    Starting from 1 September 2002, a daily output containing the coordinates of ocean, land (that is, islands and the ice sheet), ice shelf, shelf front, annual fast ice and perennial fast ice was generated. The ice-shelf edge coordinates were calculated by checking for ice-shelf cells adjacent to ocean or fast-ice cells.

  3. (iii)

    Repeat (ii) for each day until 31 August 2009.

The following algorithm was then applied to calculate the sea-ice lengths. For each shelf front and each day in the record:

  1. (a)

    Incorporate the coordinates generated by step (i) of the previous algorithm into the daily AMSR-E ASI sea-ice dataset. Define pack ice as any cell with a sea-ice concentration of ≥15%. In case of a conflict in which two different types of ice or land are present in a cell, priority is given to land, followed by perennial fast ice, annual fast ice and then pack ice. All remaining unclassified cells are then classified as ocean.

  2. (b)

    A pair of cells is chosen, where one cell is along the shelf front and the other cell is 10° N of the mean shelf-front latitude and between 12° W and 5° E of the mean shelf-front longitude (Wilkins RC and Voyeykov) or 12° W of the mean shelf front longitude and between the coastline and 10° N of the mean shelf-front latitude (Wilkins CL) (the 10° N boundary was chosen to avoid sea ice that would contaminate the swell data). A straight line ‘transect’ was calculated between these two cells (white and orange lines in Extended Data Fig. 2a,c). This leads to a higher density of sea-ice transects towards the centre of the shelf fronts (Extended Data Fig. 2a,c).

  3. (c)

    Sea-ice data are extracted for each cell along the transect. If land is present, the transect is discarded.

  4. (d)

    The effective pack-ice, annual fast-ice and perennial fast-ice lengths along the transect, \({L}_{{\rm{pck}}}^{(\mathrm{t})}\), \({L}_{{\rm{ann}}}^{(\mathrm{t})}\) and \({L}_{{\rm{per}}}^{(\mathrm{t})}\), respectively, are calculated. The effective pack-ice length is the sum of the cell lengths containing pack ice multiplied by the mean sea-ice concentration in those cells, whereas the effective fast-ice lengths are simply the sums of the cell lengths containing the relevant fast-ice type.

  5. (e)

    Repeat (b)–(d) for each possible pair of cells.

On a given day, the total effective sea-ice length for a particular transect is calculated as

$${L}_{{\rm{tot}}}^{(\mathrm{t})}\equiv {L}_{{\rm{pck}}}^{(\mathrm{t})}+{L}_{{\rm{ann}}}^{(\mathrm{t})}+{L}_{{\rm{per}}}^{(\mathrm{t})}.$$
(1)

For a chosen shelf front on a given day, the transects with the lowest third of \({L}_{{\rm{tot}}}^{(t)}\) were considered as the weakest part of the sea-ice barrier. The daily values reported for Lpck, Lann and Lper are the mean values corresponding to these transects (Fig. 3d–i). The daily Ltot was obtained from the sum of Lpck, Lann and Lper. A total sea-ice length in which each of the transects used was first normalized by its total transect length was also used (\({\hat{L}}_{{\rm{tot}}}\); Fig. 4d–f). The number of low sea-ice days in each year for which Ltot < 100 km, alongside days with Lpck ≤ 50 km, are shown in Fig. 3a–c.

Incoming ocean swell

Peak periods (Tp) and significant wave heights (Hs) were extracted from the Collaboration for Australian Weather and Climate Research Wave (CAWCR) hindcast – aggregated collection52. The CAWCR hindcast was generated using the WaveWatch III v4.08 wave model, which is forced by hourly wind and uses daily sea-ice concentration data from the research data archive operated by the National Center for Atmospheric Research (NCAR) for pre-2011 data. The hindcast is from 1 January 1979 to the present, with hourly outputs on a 0.4° spatial grid of the ocean surface, which were converted to daily maximum values for Hs and Tp. The operational range extends to 78° S. We used swell data from the hindcast for sea-ice concentrations of ≤25%, as it is unaffected by the presence of sea-ice53.

For each day over the 7-year record and each shelf front, incoming Hs and Tp were calculated from the hindcast as follows:

  1. (I)

    Obtain Hs and Tp for the hindcast cells contained within the bounds defined in (b) from the above algorithm (Extended Data Fig. 2a,c).

  2. (II)

    Retain the median Hs and Tp values.

This provided daily Hs and Tp time series for each shelf front (Extended Data Fig. 3).

Model of swell-induced shelf-front flexural stress

The model used to predict swell-induced flexural stress on the Wilkins and Voyeykov shelf fronts (Fig. 4) combines models of swell attenuation over distance due to sea-ice barriers (pack, annual fast and perennial fast)28 with a model of ice-shelf flexure in response to incoming swell30 (Extended Data Fig. 4). The models are two-dimensional (a horizontal ‘wave’ dimension and a depth dimension), time-harmonic and involve interactions between regular incident ocean waves of a prescribed amplitude (Ainc), wave period (T) and a sequence of the different ice covers. They are based on linear potential-flow theory for the water motions combined with thin-elastic-plate theory for the floating ice cover, where the Young’s modulus is set to be 6 GPa for the sea-ice barriers54 and 8 GPa for the ice shelves55.

A first model was used to predict the exponential attenuation over distance of the incident wave through the pack-ice region, such that the amplitude reduces to

$${A}_{{\rm{pck}}}\approx {A}_{{\rm{inc}}}\exp (-{\alpha }_{{\rm{pck}}}{L}_{{\rm{pck}}}/{C}_{{\rm{pck}}}),$$
(2)

where αpck(T) is the attenuation coefficient. The ice cover was modelled as an array of floes with a thickness of 0.52 m and lengths randomized about a mean value of 500 m (ref. 56) and at an average concentration Cpck. Attenuation is produced by wave scattering at the floe edges and wave energy dissipation due to drag pressure57, calculated using the Robinson–Palmer model, which gives a frequency dependence similar to observations27 with a damping parameter of 13.5 Pa s m−1 (refs. 11,54,58). The evolution of wave attenuation models, which started in the 1970s, is documented in multiple review articles (for example, refs. 59,60,61). Sensitivity studies have also been conducted, such as that in ref. 62. Three-dimensional versions of the model are available but at a far greater computational cost and without evidence of major differences in the predicted attenuation coefficients63,64.

Annual and perennial fast-ice models were used to predict the reduction in the incident waves due to reflection at the fast-ice edges and the subsequent exponential attenuation of the waves over distance through the fast-ice regions65, such that the wave amplitude reaching the shelf front is

$${A}_{{\rm{per}}}={a}_{{\rm{per}}}{A}_{{\rm{ann}}}\exp (-{\alpha }_{{\rm{per}}}{L}_{{\rm{per}}})\quad \,\text{where}\,\quad {A}_{{\rm{ann}}}={a}_{{\rm{ann}}}{A}_{{\rm{pck}}}\exp (-{\alpha }_{{\rm{ann}}}{L}_{{\rm{ann}}}),$$
(3)

a• denotes the transmitted (non-reflected) components and α• are the attenuation coefficients. The models are based on the one outlined in the seminal study by Fox and Squire66, but include the Robinson–Palmer dissipation model for attenuation, as in ref. 67. The annual fast-ice thickness was set to 2 m (ref. 68) and the perennial fast-ice thickness was 11 m (refs. 18,68).

An ice-shelf model was used to predict the vertical displacement of the ice shelf, η(x), due to flexural-gravity waves, forced by the proportion of the incident wave that reaches the shelf front, such that

$$\eta (x)={A}_{{\rm{per}}}\hat{\eta }(x),$$
(4)

where \(\hat{\eta }(x:T\,)\) denotes the displacement due to unit-amplitude forcing. The form of the model used was pioneered in refs. 42,69, and has since been extended to include an Archimedean ice-shelf draught (90% of the ice thickness)70 and varying spatial profiles of ice-shelf thickness and seabed bathymetry29. The version of model used in this study has been validated in terms of the ratio of flexural-gravity-wave to incident-ocean-wave amplitudes observed on the Ross Ice Shelf30. The model also predicts that swell is far more sensitive to changes in ice-shelf thickness than seabed variations55.

The maximum flexural stress per wave period is calculated from the displacement, such that

$$\sigma =\left\vert \frac{EH}{2(1-{\nu }^{2})}{\eta }^{{\prime\prime} }\right\vert ,$$
(5)

where E is Young’s modulus and ν = 0.3 is Poisson’s ratio. Relative to the forcing amplitude, flexural stress tends to increase monotonically with wave period in the swell regime, and is negatively correlated with the shelf-front thickness55. Owing to the underlying assumptions of plane stress and strain71, equation (5) is the only non-zero component of the stress tensor. Three-dimensional models that involve more non-zero components of the stress tensor are currently being developed72,73. However, they require numerical solution methods, which would be prohibitively expensive for the present study, and it is not yet clear in which regimes 2D model predictions of stress require the additional spatial dimension.

For each shelf front and each day over the 7-year record, the model was applied to Lpck, Cpck, Lann and Lper, which were derived as described above. The incident wave amplitude and period are set to be Ainc = 0.5Hs and T = Tp using the median significant wave height and peak period for the relevant shelf front and day, derived as described in the previous section.

Extended Data Fig. 2b,d shows model outputs corresponding to the highlighted Wilkins RC transects in Extended Data Fig. 2a,c. Exponential attenuation of swell through the sea-ice barriers is evident, along with amplitude drops at the fast-ice edges due to partial reflection of the incident waves28. The attenuation rate per kilometre is greatest in the pack ice due to the broken nature of the ice cover, and the attenuation rate is greater in annual fast ice than perennial fast ice. In contrast, the thicker perennial fast ice creates a greater amplitude drop than the annual fast ice. Once the incident wave reaches the shelf front, it imparts flexural stress as it travels through the ice shelf. The stress is responsive to variations in ice-shelf thickness, with a thickness decrease causing a stress increase, although the peak stress is away from the shelf front where the stress values are sampled.

For each shelf front and each day, the flexural stress outputs were reduced to a single value, σ, by taking the mean over 1–2 km from the shelf front for each transect and taking the mean over the transects. The interval of stress locations was chosen to be close to the shelf front but far enough away to avoid the shelf front boundary layer caused by the free-edge conditions. The accumulated stress (Fig. 4) is the weighted sum

$${\sigma }_{N}=\mathop{\sum }\limits_{n=0}^{N-1}\frac{(N-n){[\sigma ]}_{{\rm{day}}-n}}{N},$$
(6)

that is, the stress summed over an N-day window, where the weight of the stress decreases linearly with age until it moves outside the window.

Results in Fig. 4d–f were obtained using 60-day windows, which balance the responsiveness of the accumulated stress to changes in daily stress and capture build-ups over time (Extended Data Fig. 5). The normalized daily accumulated stress (\({\hat{\sigma }}_{60}\); Fig. 4d–f) is the ratio of the accumulated stress to the mean yearly maximum stress over the 7-year record for the shelf front. Corresponding results for climatological sea-ice lengths are also given (\({\hat{\sigma }}_{60}^{{\rm{aice}}}\)), which were calculated using a daily climatological average of Lpck, Lann and Lper and the same wave conditions as σ60.

Topological altimetry

The CryoSat-2 Synthetic Aperture Radar Interferometry Level-2I processing baseline-E mode was used to obtain surface elevation data to calculate ice-shelf thicknesses. The CryoSat-2 satellite was launched on 8 April 2010, and provides coverage to 88° S on a 369-day repeat cycle. For each ice shelf, all available tracks were taken from 2014–2023 within the ice-shelf boundaries from the MEaSUREs Antarctic Boundaries for International Polar Years 2007–2009 from Satellite Radar, Version 249. To account for any ice-shelf growth, a 10 km buffer zone was allowed in front the shelf front. When processing, any elevation with an accompanying ≥30 dB of backscatter was removed, following ref. 74, before outlier elevations (e) were removed if they fell outside the range

$${e}_{25}-1.5\,\times \,{\mathrm{IQR}},\,{e}_{75}\,+1.5\,\times \,{\mathrm{IQR}}.$$
(7)

A tidal-height correction using the Circum-Antarctic Tidal Simulation75, the ocean tide loading from the Finite Element Solutions 2004 tidal atlas76 and geoid from Earth Gravitational Models 1996 were used to correct altimetry data for variations in freeboard elevation. Ice-shelf thicknesses were calculated following refs. 77,78, which used

$$h=\frac{(e-\delta ){\rho }_{{\rm{w}}}}{{\rho }_{{\rm{w}}}-{\rho }_{{\rm{i}}}}+\delta ,$$
(8)

where h is ice-shelf thickness, e as the freeboard elevation, δ is the firn air content79, ρw = 1,028 kg m−3 is the water density and ρi = 917 kg m−3 is the ice density.

Individual grids were built for each ice shelf with a resolution of 3 km2 at a yearly temporal resolution. This set-up was chosen to prevent erroneous readings due to nearby ice shelves from influencing the ice-shelf thickness output, and to reduce processing time and counteract a lower density of altimetry tracks near the edge of the ice shelf77. The distance of each grid cell from the shelf front was calculated, with only grid cells within 20 km of the shelf front retained to represent the approximate area lost in each calving. Each grid cell from 2014–2023 was combined, using the IQR method to remove outliers, such as those that picked up the surrounding ice sheet or fast ice. Quartiles were calculated for each ice shelf analysed in Fig. 5b that did not have a defined pre-calving ice-shelf thickness.