Main

The formation and evolution of rift zones is a primary tectonic process that shapes Earth’s surface. Observations from tectonically mature rifts show that the principal mode of upper-crustal extension in these settings is aseismic magmatic rifting by dyke intrusion1,2,3. At intermediate-to-low extension rates (<75 mm yr−1), this magmatic rifting process is highly episodic4,5,6, characterized by active phases of repeated magma intrusions and volcanic eruptions within narrow (~20-km-wide by ~60-km-long) axial rift zones or segments5,7,8,9,10,11. By contrast, at less tectonically mature rift systems, seismic or mixed (tectonic–magmatic) modes of extension are more prevalent, with normal faulting having an important role in accommodating strain across broad (~50–100-km-wide) grabens alongside sparser, more distributed magmatic activity12,13,14. The maturation of a continental rift towards a mid-ocean ridge is therefore characterized by the construction of narrow intrarift zones of magmatic accretion, reflected by concurrent transitions in rift width, morphology and surface geology14.

Key to the seismic-to-magmatic rift transition is the development of magma plumbing systems that can efficiently feed melts into the upper crust to build magmatic rift zones13. Once established within the crust, the magmatic architecture of these focused rift zones can facilitate concentrated crustal extension, via dyke-induced spreading in the upper crust and the thermomechanical modification of the lower crust1,2,3, accompanied by progressive ductile thinning of the underlying mantle lithosphere15. Constraining how and when magmatic rift architecture develops during the lifetime of continental rifts, and the dynamics of magma ascent through this architecture, is essential for comprehending the transition from seismically dominated rifting to magmatically driven continental break-up.

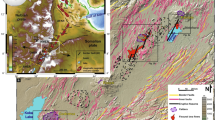
The Main Ethiopian Rift (MER) is an active continental rift system within the northern East African Rift System (EARS) (Fig. 1). Bridging the seismically dominated graben-bound rift basins in the southern EARS and the spatially focused magmatic rift zones in Afar, the MER is considered to represent an intermediate stage of continental rift evolution13,16,17. Geophysical data suggest that present-day extension in the MER has migrated from seismic displacement along large graben-bounding faults to predominantly aseismic rifting within segmented intragraben magmatic rift segments since 2 Ma (refs. 13,17,18,19). These axial rift zones or segments are characterized at the surface by closely spaced faults and fissures, large silicic volcanoes and aligned basaltic scoria cones and fissural lavas (Fig. 1). Rift-parallel seismic anisotropy provides evidence for concentrated dyke emplacement within these sections of the MER, indicating that magma intrusion has had an important role in the accommodation of recent intrarift extensional strain20,21. Nevertheless, unlike Afar, only ~30% of the 25–40-km crust under these magmatic segments is igneous14, while the continued presence of a relatively thick lithosphere suggests that the MER has not progressed to an advanced stage of tectonic maturity22,23.

Fig. 1: Maps showing the Boku Volcanic Complex and the East Ziway cone field in the MER.
figure 1

a–c, The two markers show the location of the individual cones from which our samples are collected (a), at the Boku Volcanic Complex (b, red triangle) and East Ziway cone field (c, blue circle). The digital elevation model is the Shuttle Radar Topography Mission (SRTM)45,46; faults are collated from ref. 47; magmatic segments are redrawn after refs. 16,17; rift volcanoes and major faults shown in the inset map in a are collated from the Smithsonian Global Volcanism Program (volcano.si.edu; accessed 25 May 2025) and the BGS/NERC EARTH dataset (item 132705), respectively.

Full size image

In this study, we constrain the timescales and dynamics associated with the transit of basaltic magmas through the MER crust, with the aim of characterizing the ascent rates and pathways of magmas that feed upper-crustal dyke intrusions. Our results stem from an investigation of the intracrystal record of magmatic processes provided by the mineral olivine ([Mg,Fe]2SiO4). The Fe/Mg ratios of olivine crystals, expressed as the forsterite number (Fo = 100 × Mg/[Mg+Fe], in mol.%), reflect those of the magmas they crystallize from, with higher Fo olivine crystallizing from more primitive (high MgO) and hotter basaltic magmas24. Compositional disequilibrium between olivine crystals and magmas can occur during transport and storage as a result of rapid changes in ambient magma composition, pressure, temperature and/or oxygen fugacity, producing chemical zonation within growing crystals. Furthermore, Fe–Mg interdiffusion between intraolivine zones is rapid at magmatic temperatures and acts to relax initially sharp compositional boundaries25. By quantifying and modelling the temporal evolution of observed compositional gradients within olivine crystals, timescales corresponding to the interval between initial magmatic disequilibrium and the final quenching of the crystals during eruption can be estimated (hours to decades25,26,27). We therefore aim to constrain the dynamics of magma ascent within crustal plumbing systems before intrusive-eruptive rifting events, exploiting this geochemical record for erupted MER magmas.

Compositional zoning patterns in MER olivine crystals

Our samples are from two Quaternary (~200 ka, ref. 28) scoria cone fields located in an MER rift segment: the Boku Volcanic Complex29 (36 olivine crystals; Fig. 1b) and the East Ziway cone field30 (43 olivine crystals; Fig. 1c). Crustal thickness in this region is ~35–40 km, with marginally thinner crust beneath Boku relative to Ziway31,32, consistent with geochemical evidence of increasing MER tectonic maturity from south to north33,34. Melt inclusion geobarometry reveals that ascending basaltic melts beneath this part of the MER stall at mid-crustal depths (10–15 km deep), forming a vertically narrow zone of magmatic intrusion comprising semi-discrete sills3,35, mirroring magma storage in more mature rifts36. The bulk of olivine crystallization beneath the MER probably occurs within this mid-crustal zone, driving the evolution of erupted MER lavas away from primitive magma compositions (for example, refs. 33,37).

Olivine crystals from both localities, picked from sieved disaggregated scoria, are 1–4 mm and are subhedral with 5–10 μm irregular dendritic rims (Fig. 2a–c and Supplementary Figs. 5–31). Individual olivine crystal cores are compositionally homogeneous, but display a broad compositional range within our sample suites at both Boku (Fo69–87; Fig. 3a,b) and Ziway (Fo63–88; Fig. 3c,d). The variety of olivine compositions we observe therefore suggests that crystallization occurred over a broad range of melt compositions and/or temperatures. Intracrystal Fo zoning is clearly observed in backscatter electron (BSE) imagery (mean core–rim Fo difference of 6 mol.%; Fig. 2), and we identify two populations, common to both localities, with distinct core-to-rim zoning patterns (length scale of <160 μm): population 1 olivine crystals are ‘normal-zoned’ with higher Fo cores and lower Fo rims (Fig. 2a); population 2 crystals are ‘reverse-zoned’ with lower Fo cores and higher Fo rims (Fig. 2b,c).

Fig. 2: BSE images of compositionally zoned olivine crystals from MER scoria cones and their rim-to-core compositional profiles.
figure 2

a–c, BSE images showing population 1 olivine (a), population 2 olivine (b) and detail of b (c). BSE greyscale is proportional to olivine Fo; dark and bright regions are high- and low-Fo, respectively. d,e, Olivine compositional profiles of a (d) and b (e) (electron probe and calibrated BSE greyscale) with diffusion-only model curves. f, Growth–diffusion model curve for olivine in b. Inset stereographic lower hemisphere plots in d and f illustrate profile traverse trends (trav.) relative to olivine crystallographic orientation (defined by the axes a, b, c).

Full size image
Fig. 3: Violin plots illustrating MER olivine core and rim compositions.
figure 3

a–d, Boku olivine compositions (normal-zoned population 1 crystals and reverse-zoned population 2 crystals in a and b, respectively) and Ziway olivine compositions (normal-zoned population 1 crystals and reverse-zoned population 2 crystals in c and d, respectively). Compositions are obtained from electron-probe-calibrated BSE greyscale compositional profiles (n is the number of crystals). Medians of each distribution are shown as vertical dashed lines, and 95% confidence intervals are provided by the error bars. Gaussian approximation is used to determine violin bandwidth. Dotted and solid grey lines respectively show mean equilibrium olivine from matrix glass and whole rock compositions from the two cones studied, assuming an olivine–melt Fe–Mg distribution coefficient of 0.30 (ref. 24).

Full size image

Reverse-zoned population 2 crystals dominate both sample sets (Fig. 3). At both localities, the cores of population 2 olivine are both lower Fo and exhibit a broader range in Fo than population 1 (Fig. 3). In addition, Ziway olivine cores and rims are typically lower Fo than their counterparts from Boku, mirroring the more compositionally evolved basaltic lava compositions observed at Ziway relative to Boku (higher SiO2 and lower MgO; Fig. 3 and Supplementary Data 1). The boundaries of population 1 and 2 crystal rims are straight, suggesting that they follow a euhedral palaeo-rim of the crystal (Fig. 2). By contrast, the outermost dendritic rims exhibit short-length-scale (~10 μm) normal zones, which follow the irregular rim morphologies instead of interior crystal zones (Fig. 2c), characteristic of rapid late-stage growth rather than diffusion38. Discounting these late-stage overgrowths, the low-Fo population 1 rims and population 2 cores are closest to chemical equilibrium with their matrix glasses at both localities (Fig. 3).

Olivine Fe–Mg interdiffusion chronometry

We determine olivine Fe–Mg interdiffusion timescales using two modelling approaches (see the Methods for full details). The first model correlates 72 measured olivine compositional profiles to model diffusion profiles, with the simplifying assumptions that diffusion occurs isothermally and that the crystal does not grow (the Autodiff ‘diffusion-only’ model39; Fig. 2d,e). These assumptions permit a time-efficient method of extracting timescale data from large numbers of crystals.

To test the validity of the diffusion-only results, we also apply a second, more complex model to a subset of 31 crystal profiles, which simulates simultaneous crystal growth and diffusion in a chemically evolving and cooling melt40,41 (Fig. 2f). As anticipated, the combined growth–diffusion model can provide better fits to the complex compositional profiles we observe—that show evidence for considerable growth accompanying diffusive equilibration (Fig. 2e,f)—and in general returns slightly shorter timescales than those predicted by the diffusion-only method. However, for the same olivine profiles, timescale differences between the two models are generally not considerable, and within the same order of magnitude (Methods and Supplementary Fig. 3). Owing to the simplifying assumptions, the diffusion-only model is therefore considered to return maximum timescales that slightly, but not substantially, overestimate the duration of diffusive equilibration relative to the growth–diffusion model.

In all cases, MER olivine Fe–Mg interdiffusion timescales are shorter than a year, and typically around a few months (Fig. 4). The distributions of timescales recorded for each population are similar between the two localities, and we observe no correlation between timescales and olivine core or rim compositions (Fig. 4 and Supplementary Data 1). Where multiple profiles are analysed for an individual crystal, timescales are self-consistent. Population 1 olivine crystals trend primarily towards the higher end of the diffusion-only timescale distribution and range from 36 to 343 days (log-mean: 139 days; Fig. 4a,c). Population 2 diffusion-only timescales are broad, but are typically shorter than those from population 1, and range from 1 to 236 days and 2 to 94 days for Boku and Ziway, respectively (respective log-means: 40 days and 17 days; Fig. 4b,d). By comparison, timescales from the growth–diffusion model are more condensed, with a narrower overall range for both populations and localities of 10–104 days (log-mean: 27 days; Fig. 4e,f). Overall, our results constrain intracrystal disequilibrium at both localities to have occurred in the weeks to months before eruption.

Fig. 4: Cumulative frequency plots of Boku and Ziway olivine Fe–Mg interdiffusion timescales.
figure 4

a–f, Diffusion-only (a–d) and growth–diffusion (e and f) models (n is the number of profiles). Diffusion-only timescales (log-mean ± 1 log-standard-deviation) are separated by olivine population (Pop.), with population 1 timescales illustrated in a and c, and population 2 timescales in b and d; crystals of the other population at the same locality are included as faded markers and curves. The growth–diffusion timescales illustrated in e and f (Bou and Ziway, respectively) include both populations. Faded curves in e and f represent all diffusion-only timescales at Boku and Ziway, respectively. Diffusion-only timescales are calculated at fixed temperatures, shown within a–d. Growth–diffusion timescales are obtained at variable initial olivine–melt system temperature (Methods). Kernel density curves in log-space use Gaussian approximation to determine bandwidth, and relative probability density is consistent across all panels. Note that some timescales are recorded from the same crystal.

Full size image

Magmatic dynamics and architecture in the MER

The olivine zoning patterns and Fe–Mg interdiffusion timescales from both locations studied here are notably similar (Figs. 3 and 4). This strongly suggests that the dynamics of magma ascent and crystal–melt interaction are largely common along this part of the MER, with crystal–melt chemical disequilibrium consistently occurring weeks to months before intrusive-eruptive events. At both localities, the majority of olivine crystals are reverse-zoned population 2 crystals (Figs. 3 and 4), which probably result from the rapid growth of high-Fo olivine rims on preexisting lower Fo olivine crystal cores during mafic magma recharge events. The homogeneous cores of all olivine crystals suggests that no disequilibrium is recorded before rim growth, indicating either that the crystal grew in equilibrium with an evolving host magma or that the timescales between disequilibrium-driving events are sufficiently long enough to erase evidence of previous magmatic disequilibrium. Population 1 olivine cores are closest to equilibrium with primitive high-MgO mantle-derived melts (which crystallize Fo~90 olivine), and rim growth and diffusion is possible only by emplacing these crystals in a more chemically evolved lower MgO melt. By contrast, population 2 olivine cores are lower-Fo, suggesting that these crystals are already present within compositionally evolved crustal melt bodies when magmatic disequilibrium is triggered via the input of high-MgO magma.

Our results, in combination with other studies3,20,35 and summarized in Fig. 5, are consistent with a magmatic architecture for MER rift zones characterized by regions of basaltic magma storage distributed throughout the mid-to-lower crust (Fig. 5a). Melt inclusions suggest that there is limited chemical communication between melts stored in the mid-crust3 (~10–15 km), consistent with a mush-dominated system assembled by successive batches of melts, separated by either time or space, from which low-Fo population 2 cores are derived. Ascending mafic recharge melts bearing high-Fo population 1 cores from the lower crust are mixed into the more-evolved magmas already resident in the shallower crust, driving intracrystal chemical disequilibrium and the onset of concurrent rim growth and diffusive equilibration (Fig. 5b,c). We find no evidence for magma recharge timescales exceeding a year (Fig. 4), indicating that magma ascent towards the mid-crust only occurred weeks to months before the initiation of an intrusive-eruptive event in the upper crust. During eruption, all crystals are overgrown by narrow rims of dendritic olivine (Fig. 5d).

Fig. 5: Schematic diagram illustrating our proposed model for preeruptive intrusion in the MER as recorded by olivine Fe–Mg interdiffusion timescales.
figure 5

The stages leading up to an intrusive-eruptive event are presented. a, Magma reservoirs forming population 1 (lower crust) and population 2 (mid-crust) olivine crystals are separated before intrusion. b, In the weeks to months before eruption, intruding magmas from the population 1 reservoir carrying population 1 olivine crystals enter the population-2-forming sill network, triggering magmatic disequilibrium. c, This disequilibrium causes simultaneous olivine rim growth and Fe–Mg interdiffusion, affecting both population 1 and 2 crystals. d, Ascent and eruption drives final short-length-scale dendritic overgrowth on all crystals.

Full size image

Rapid melt recharge before magmatic rifting in the MER

The magmatic architecture and ascent dynamics that we propose for the MER (Fig. 5) implies that upper-crustal magmatic rifting events in this part of the EARS are largely driven by processes occurring within an ensemble of mid-crustal sills3,42. Our olivine Fe–Mg interdiffusion timescales probably record magmatic disequilibrium resulting from precursory replenishment of these sills in the weeks to months preceding upper-crustal dyke intrusion and eruption.

This model for magma dynamics and storage in MER rift zones is notably similar to those recently proposed for intrusions in the Reykjanes Peninsula, Iceland36, and more generally for monogenetic eruptions43. Furthermore, the weeks-to-months timescales of crustal magma transit recorded in our data are comparable to the time intervals between dyke intrusions constrained by geophysical observations during rifting episodes at the Manda Hararo-Dabbahu Rift in Afar, Ethiopia (2005–2010)5,7,10, and in Iceland, at Krafla (1975–1984)5,8,9,11 and the Reykjanes Peninsula (2023 to present; volcano.si.edu/volcano.cfm?vn=371020; May 2025) (Fig. 6). During the Dabbahu7 and Krafla8 episodes, crustal magma reservoirs underwent inflation–deflation cycles on the order of a few months as magmas ascended from the lower crust, replenished melt reservoirs and then intruded along the rift as shallow dykes. These observations indicate a rifting process whereby ascending magmas instigate and then, via ongoing recharge, sustain periods of extensional activity. Conversely, the 2007 rifting event in the Natron Basin, Tanzania—a less mature sector of the EARS—began with seismicity on normal faults without detectable magmatic activity, closely followed by a single dyking event in the upper crust that was probably facilitated by faulting-induced stress changes12,44.

Fig. 6: MER olivine timescales within the context of other subaerial rifting episodes.
figure 6

a, Growth–diffusion timescales (markers) and cumulative frequency distribution of all diffusion-only timescales (thick grey line is log-mean; 1 log-standard-deviation within dashed lines). b, Violin plots of time intervals between the onset of dyke intrusions as resolved by geophysical methods, with log-medians represented as vertical lines. Kernel density plots in log-space use Gaussian approximation to determine bandwidth. Dyke recurrence timescales assessed from refs. 7,10 for Dabbahu (13 events), refs. 8,11 for Krafla (19 events) and the Smithsonian Institution Global Volcanism Program website (volcano.si.edu/volcano.cfm?vn=371020; accessed 25 May 2025) for Reykjanes (7 events).

Full size image

Based on these observations, our results suggest that melt transport dynamics in the MER are comparable to more mature magmatic rifts versus the less mature southern EARS and that the magmatic architecture necessary to facilitate tectonically mature rifting has already been established in the MER. Notably, this has occurred before substantial thinning of the crust32 or lithosphere15,23,31. Overall, our results support models that highlight the importance of magmatism to rift evolution and therefore show that a robust magma supply from depth probably drives rift development before substantial plate thinning in the MER.

Methods

Sample preparation

Fresh olivine crystals were picked from disaggregated scoria collected from the Boku and East Ziway cone fields (Fig. 1), mounted in epoxy and polished to 0.25-μm grade using silicon carbide papers, diamond pastes and Syton polishing fluid. Samples were fully carbon coated before analysis to promote conductivity.

X-ray fluorescence

Scoria and lava samples from cones and basalt fields in the Boku Volcanic Complex and East Ziway cone field were powdered with an agate ball mill at the University of Leeds to 150-μm grade. X-ray fluorescence (XRF) on these samples was performed using the Rigaku ZSX Primus WDXRF at the University of Leeds by Lesley Neve on our behalf during the COVID-19 pandemic. Before analyses, all samples were dried at 105 °C to remove remaining moisture. Loss on ignition was assessed by heating the samples to 1,025 °C for at least 1 h. A 1:10 ratio of sample:flux (comprising 66% Li2B4O7 and 34% LiBO2), supplemented with three drops of LiI, was used to create fused beads. Sample–flux mixtures were cast at 1,150 °C for 20 min in platinum crucibles to allow the sample to dissolve. Once molten, the beads were allowed to cool to room temperature and cleaned with 25% HCl. The standards USGS BCR-1 and STSD-4 were run at the start of the session and at regular intervals throughout. Detection limits were 0.03 wt.% for MgO and Na2O, and 0.01 wt.% for all other elements.

Supplementary Data 1 includes East Ziway whole rock XRF data; the Boku data shown in Fig. 3 have previously been published3.

Scanning electron microscopy

BSE imaging and electron backscatter diffraction (EBSD) were performed using the Cameca FEI Quanta 650 scanning electron microscope at Leeds Electron Microscopy and Spectroscopy Centre (LEMAS), University of Leeds, using a 20-kV 6-μm beam on Aperture 3. BSE images of olivine diffusional zones were captured at high contrast at a magnification of >2,000×. In a subsequent analytical session, regions of 1,000–10,000 pixels of size 5–15 μm were mapped within each crystal using EBSD. Initial data reduction to remove crystal pseudosymmetries (solutions resulting in multiple possible crystal symmetries) and null pixels was performed using Oxford Instruments Channel 5 Aztec Crystal software. Where extreme degrees of pseudosymmetry were present, each pseudosymmetry was characterized and assessed separately for diffusion timescales. If a region of the crystal had a symmetry that did not match that of the core, it was assumed to be a subgrain and removed from the mapped region. One crystal (ZA_D1) could be fit with two possible crystal symmetries. For this crystal, we provide two possible timescales for each crystal symmetry (ZA_D1_N_1 and ZA_D1_N_2). The Autodiff diffusion-only timescales of 48 days and 65 days respectively derived from these two symmetries are within mutual uncertainty and therefore do not affect the outcomes of our study. All images are available in the Zenodo repository at https://doi.org/10.5281/zenodo.14038707 (ref. 48).

Uncertainties in obtaining timescale information from diffusion profiles were mitigated through careful selection of traverse direction. We selected traverses perpendicular to the crystal face (or diffusional front) that also pass through the centre of the crystal. Traverses inclined relative to crystal rims were avoided, as they produce a greater apparent diffusion timescale26. Further guidelines established by previous literature26,49 were followed wherever suitable and possible.

In this study, sectioning angles are assumed to be perpendicular to crystal faces. While shallow sectioning will result in longer timescales27, the relative size of the crystal is large relative to profile distances, and the magnitude of resultant sectioning uncertainty may be minor relative to uncertainties propagated from the diffusivity, especially given the large population of crystals comprising the dataset of this study40. In most cases, profiles collected from the same crystal return self-consistent modelled timescales (that is, within 1 log-standard-deviation uncertainty).

Electron probe microanalysis

Electron probe microanalysis (EPMA) for olivine and matrix glass compositions were performed using the JEOL JXA8230 at LEMAS, University of Leeds, using five spectrometers with TAP, TAPH, LIFH, PETJ and LIFL analysing crystals (standards, count times, and beam conditions are provided in the Supplementary Information). Compositional traverses from olivine rims to cores comprising 10–20 points spaced ~5–15 μm apart were measured. The lengths of the extracted profiles themselves were chosen dependent on the apparent width of diffusion observed through BSE imaging. The starting spot of each EPMA traverse was taken ~5 μm outside the crystal to determine the traverse point where the olivine crystal had been entered. Where possible two compositional traverses were taken from different orientations within the same crystal49. EPMA profiles are included in Supplementary Data 1.

Calibration of BSE profiles to EPMA points

High-resolution Fe–Mg interdiffusion profiles were obtained using BSE images. Because of the electron backscattering effect, regions of the olivine crystal that are more Fe-rich (low Fo) will appear brighter in greyscale contrast in BSE images than olivine regions that are more Mg-rich (high Fo). The pixel-scale resolution of backscatter images (~0.1 μm) can therefore provide a substantial increase in datapoint resolution relative to EPMA (5–20 μm), which can be used to characterize the compositional profile of olivine crystals.

Using BSE images, greyscale values along measured profiles were extracted perpendicular to crystal edges, or perpendicular to diffusion fronts if diffusion was not parallel to crystal edges, using ImageJ software50. BSE profiles were subsequently calibrated with EPMA data to obtain high-resolution distance profiles in olivine Fo; BSE and EPMA traverses have similar profile shapes whose values can be related by a linear function. Exploiting this linear proportionality, the shape of the BSE profile was manually fitted to the EPMA profile by minimizing the misfit χ2 (equation (1)):

$${\chi }^{2}=\mathrm{ln}\left(\frac{{\sum }_{i=1}^{n}{\left|{X}_{{\rm{Fo}},i}-\left({g}_{i} m+c\right)\right|}^{2}}{n}\right),$$
(1)

where n is the number of probe points i present within the BSE profile, XFo,i is the compositional value in Fo of point i obtained by EPMA (where XFo = Fo/100), gi is the corresponding greyscale value of that point in the BSE profile (between 0 and 255) and m and c are the respective gradient and intercept of the linear function relating greyscale to Fo. The gi corresponding to XFo,i for each EPMA datapoint was determined through linear interpolation of the nearest two BSE greyscale values to the point. χ2, m and c were determined using the optimize.minimize function of the Python library SciPy51 for all EPMA datapoints after initial visual alignment of BSE and EPMA profiles. The lateral offset of BSE profiles relative to EPMA profiles was also corrected during the minimalization process.

BSE and EPMA profiles were individually assessed for anomalies (for example, cracks and small mineral or melt inclusions) before fitting to ensure successful calibration. All BSE and EPMA profiles were assumed to be parallel; major angular differences between the profiles (>10°) will result in poor correlations between traverse distances in the diffusing region; profiles exhibiting poor fits between BSE greyscale points and EPMA points were not considered. Where multiple different fits between BSE and EPMA were possible, the fit with the lowest misfit was chosen; otherwise the profile was not considered for the final dataset. Using this approach, all greyscale profiles in this study are calibrated such that linear R2 between BSE and EPMA data is >0.98. All m, c and lateral shift values are provided in Supplementary Data 1, images demonstrating BSE and EPMA fits are available in the Zenodo repository at https://doi.org/10.5281/zenodo.14038707 (ref. 48) and all compositional profiles calibrated with this method are illustrated in Supplementary Fig. 1.

Diffusion modelling using Autodiff (diffusion-only) model

Diffusion timescales are extracted from compositional profiles in olivine using an edge-buffered diffusional model39,52 (equation (2)):

$$\begin{array}{c}t=0,C={C}_{0}\,{{{\rm{for}}\;{\rm{all}}}}\,x\\ t > 0,C={C}_{1}\,{{{\rm{for}}\;{\rm{all}}}}\,x < 0\,{\rm{and}}\,{C}_{x,t}=f(C,x,D,t)\,{{{\rm{for}}\;{\rm{all}}}}\,x\ge 0\end{array},$$
(2)

where C0 is the initial composition of the olivine crystal, C1 is the external buffer composition for t > 0, D is diffusivity and x is distance, where x = 0 is the edge of the crystal. This model assumes that diffusive exchange occurs from the rim to the core of the crystal, with the rim in diffusive communication with the surrounding magma, and that the initial compositional profile of the olivine crystal is a homogeneous core. While some profiles can be fit well with an initial step condition, edge-buffering is preferred to provide good quality fits to the diffusional curve and to keep consistency across all profiles. All diffusion profiles were fitted using the Autodiff Excel code39, which assumes isothermal and isobaric olivine reequilibration conditions. Profiles that could not be fit using Autodiff were rejected.

A key uncertainty is associated with the diffusivity D, resulting from uncertainties in (1) the experimental calibration of diffusion53,54 and (2) the thermodynamic conditions of magmatic storage (that is, temperature, pressure and oxygen fugacity55). Temperature contributes the greatest uncertainty owing to the Arrhenian form of D (refs. 26,53,54), and uncertainties of ~20–30 °C can affect calculated timescales by a factor of 2–4 (ref. 26). The sum of individual uncertainties on D are close to log-Gaussian and can be propagated in log-units27; timescale uncertainties are therefore asymmetric in absolute time. In this study, uncertainties in temperature, pressure, oxygen fugacity and backscatter pixel resolution are propagated through Monte Carlo error propagation (n = 10,000) alongside uncertainties from the original experimental calibration of diffusivity53,54.

Autodiff assumes diffusion occurs within an isothermal and isobaric magmatic environment. Conditions at Boku were assumed to be 1,180 ± 20 °C (refs. 23,56) and 3 kbar (ref. 3). At Ziway, where there are few direct observations of magmatic storage conditions, we assume a temperature and pressure at population 2 rims will crystallize from a primitive melt (Fo74–80; Fig. 3). Through thermodynamic petrological modelling with RhyoliteMELTS v1.2.057 from a starting Ziway basalt composition (Z58; Supplementary Table 1), we estimate temperature to be 1,130 ± 30 °C (Supplementary Fig. 2). Pressure has a limited effect on olivine composition during fractionation (Supplementary Fig. 2), and is assumed to be 3 kbar following melt inclusion geobarometric observations made at Boku3. Oxygen fugacity in the MER is well established at the quartz-fayalite-magnetite buffer (QFM ) ± 1 log units (refs. 58,59), and basalt H2O ranges of 1.0 ± 0.5 wt.% (refs. 3,35). Using these conditions, we obtain Fe–Mg interdiffusion fits to 72 profiles in 58 MER olivine (32 profiles in 26 Boku olivine; 40 profiles in 32 Ziway olivine; Supplementary Data 1).

Diffusion modelling using growth–diffusion

The principal advantage of the semi-automated Autodiff approach is time efficiency. However, while the simple Autodiff model does not require substantial computational time, it can only be used to fit portions of olivine compositional profiles and cannot reproduce the overall shape of reverse-zoned Population 2 profiles. In addition, Autodiff assumes that olivine rim growth and diffusion occurred independent of each other, whereas population 2 olivine betray a more dynamic system: that is, that olivine rim growth and diffusion occur simultaneously within a cooling and compositionally evolving magmatic environment. Melt evolution and cooling will affect (1) the composition of equilibrium olivine as crystallization proceeds, and (2) diffusivity, a function of temperature and melt oxygen fugacity.

To determine if our Autodiff timescales remain reconcilable and meaningful within the context of a dynamic system, we utilize a one-dimensional model that accounts for simultaneous olivine growth and diffusion in a cooling melt40,41. In this approach, the initial olivine conditions—the composition of the olivine before olivine rim growth and diffusion—is assumed to be uniform, with the observed Fo composition of the olivine core plateau. In addition, initial olivine growth rate, a parameterized liquid line of descent linking olivine Fo and temperature, an initial magmatic temperature and cooling rate are input into the model. With every timestep, simultaneous olivine growth and diffusion, both controlled by the composition and temperature of an evolving host melt, are applied to our model olivine profile. Through iteration along the cooling path of the host melt, the degree of olivine growth and diffusion (both functions of magmatic temperature) are determined at each new timestep, resulting in a new compositional profile. The compositional profiles determined by model iteration are then compared with our observed profile. While this approach can replicate the overall shape of the olivine profile we measure, the principal downside is that iteration over the full parameter space and assessment of fit must be performed manually and by eye, which hinders the time efficiency of this approach. Because of the wide parameter space involved in this model, timescale uncertainties are complex to assess and would necessitate iteration over the full parameter space through a Monte-Carlo-like method. We believe, however, that the magnitude of uncertainties would be similar to those from Autodiff (about ±0.25 log units in this study).

The composition of olivine growing on crystal rims is controlled by the composition of the crystallizing melt, which dictates olivine composition along the liquid line of descent. To obtain olivine liquid lines of descent, we select primitive (high-MgO) basalt compositions from basaltic scoria cones from Boku (NB0129) and Ziway (Z67; determined by XRF) and determine their olivine fractionation paths using Petrolog 3.1.1.360 at 3 kbar and QFM. Fractionation of olivine, plagioclase and clinopyroxene are modelled with the parameterizations of ref. 61. These parameterizations between olivine Fo and temperature are presented in Supplementary Table 2.

We apply this growth–diffusion model to a subset of our diffusional profiles (21 profiles in 17 Boku olivine; 10 profiles in 7 Ziway olivine). Our results are shown in Fig. 4 in the main text and compared with corresponding Autodiff results in Supplementary Fig. 3. Timescales resolved using this method range from 10 to 104 days for all MER samples, with a log-mean of 27 days. Compared with Autodiff (1–343 days; log-mean of 32 days), the growth–diffusion timescales are of a similar magnitude (that is, within the uncertainty of the Autodiff timescales) or shorter in timescale (Supplementary Fig. 3). This is especially evident for the normal-zoned population 1 olivine (for example, AA_A7_E and ZA_F5_SE). The principal reason for this timescale offset is temperature sensitivity, which affects Fe–Mg interdiffusion rates. High Fo core population 1 olivine crystals begin diffusing rapidly at the onset of basalt crystallization, and the rim olivine crystallizing is of Fo lower than the core itself. As a result, the low Fo rims around population 1 olivine can be generated faster than assuming isothermal diffusion without growth. This is especially evident for Ziway population 1 olivine crystals, which return timescales similar to population 2 olivine, as diffusion now occurs at higher temperatures than the isothermal 1,130 ± 30 °C assumed for Autodiff. We therefore demonstrate that the Autodiff timescales, of similar magnitude to the growth–diffusion timescales, can be considered maximum timescales of disequilibrium and therefore meaningful in the context of this study.

Growth rates in our models are typically ~10−12–10−11 m s−1, and cooling rates are highly variable (0.001–0.4 °C h−1; Supplementary Fig. 4), although the magnitude of these parameters are consistent with previous studies using the same methodology40,41. No correlation is observed between timescale and temperature (Supplementary Fig. 4a), but shorter timescales appear to correlate with rapid cooling and faster growth (Supplementary Fig. 4b,c). Peak magmatic temperatures at which profiles are best fit by the growth–diffusion model—that is, the temperatures from which the olivine–melt system is cooled—range substantially from 1,064 to 1,225 °C. This broad range of cooling rates and magmatic temperatures can be reconciled if melts in the Ethiopian mid-crust remain sufficiently isolated from each other during fractionation3.

Finally, we highlight three cases that demonstrate the possible limitations of the growth–diffusion model (see Supplementary Fig. 3 for profile references). We note, however, that in each of these cases the resultant timescales do not substantially affect the outcomes of our study.

  1. (1)

    Growth–diffusion timescales recorded from different profiles on the same crystal are generally self-consistent, which is also observed from Autodiff models. An exception to this is the crystal ZA_B4, with two profiles (ZA_B4_NW and ZA_B4_NNW) differing by 15 days (Supplementary Figs. 28 and 29). This could result from an inclination between the polished sectioning surface and the crystal face, which would stretch the anisotropy predicted from a vertical profile by a factor of ~1.4–1.5 as observed here if not perpendicular39. We note that both timescales remain within the uncertainty envelope of the corresponding Autodiff timescale of ZA_B4_NNW.

  2. (2)

    We resolve two possible model profiles for a population 1 profile (AA_D1_SW), with similar visual degrees of fit (AA_D1_SWa and AA_D1_SWb; Supplementary Fig. 31), which is the product of different cooling and growth rates. In other words, the manual fitting of this profile using the growth–diffusion model provides non-unique timescale solutions (21 days and 42 days), which is a by-product of the complex parameter space utilized by the growth–diffusion model.

  3. (3)

    Two population 2 profiles (AA_D4_N and AA_D5_W) are fitted assuming a stepped initial compositional profile, unlike the flat initial condition with uniform Fo reflective of the olivine cores assumed for other model fits (Supplementary Fig. 31). Qualitatively, this initial condition assumes very rapid growth of the high Fo rim before further growth, cooling and diffusion. As a result, the shape of the olivine reverse rim is highly affected by diffusion at high temperature, whereas the lower Fo exterior rim is principally affected by late-stage growth at low temperature. While timescales returned from this stepped initial condition are similar to other growth–diffusion models, the final magmatic temperature is substantially cooler and reflects the necessity for late-stage lower Fo growth.