Human motor cortex encodes complex handwriting through a sequence of stable neural states

Abstract

How the human motor cortex (MC) orchestrates sophisticated sequences of fine movements such as handwriting remains a puzzle. Here we investigate this question through Utah array recordings from human MC during attempted handwriting of Chinese characters (n = 306, each consisting of 6.3 ± 2.0 strokes). We find that MC activity evolves through a sequence of states corresponding to the writing of stroke fragments during complicated handwriting. The directional tuning curve of MC neurons remains stable within states, but its gain or preferred direction strongly varies across states. By building models that can automatically infer the neural states and implement state-dependent directional tuning, we can significantly better explain the firing pattern of individual neurons and reconstruct recognizable handwriting trajectories with 69% improvement compared with baseline models. Our findings unveil that skilled and sophisticated movements are encoded through state-specific neural configurations.

Main

Humans are superb at controlling sophisticated fine movements, such as writing, typing and musical performance^1,2. These sophisticated motoric behaviours are often decomposed into a sequence of simpler movements^3,4,5,6. For example, a word is decomposed into a sequence of letters, a letter can be further decomposed into strokes, and even a stroke may involve a complex movement trajectory. Such decomposition can reduce the complexity and shorten the timescale of each movement unit, which is of particular importance for the motor cortex (MC), since neurons in the MC generally show relatively simple tuning to movement features^{7,8,9,10,11,12}, and the tuning varies over relatively long timescales¹³. It remains unclear, however, if primitive units exist during fine movement and how such units may be encoded in the MC.

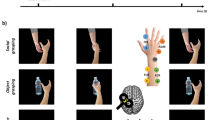
Handwriting, a skill developed through years of deliberate practice, serves as an example of sophisticated fine motor control in humans. This study investigated the neural basis of handwriting by recording single-unit neural activity from human MC with two 96-channel Utah microelectrode arrays in the left hand knob area of the precentral gyrus¹⁴ (Fig. 1a and Supplementary Fig. 1a). We studied attempted writing of Chinese characters (Fig. 1b,c), which are highly complex (>3,500 frequent characters composed by 32 types of stroke) and pose a great challenge for motor control. We identified that, during the writing of a character, the directional tuning of neurons alternates among a few stable states, each encoding the writing of multiple different small fragments of a character (Fig. 1d–f). Furthermore, the neuronal tuning during handwriting clearly changes across states (Fig. 1g). Computational models that decompose the writing process into a sequence of states better explain spiking activity from individual neurons (229% change) and better decode the handwriting based on the neural population (69% change; Fig. 1h), compared with a model that assumes stable neuronal tuning throughout the writing of a Chinese character.

Fig. 1: The handwriting task and neural representation during attempted handwriting.

a, The participant has two 96-channel Utah intracortical microelectrode arrays implanted in the left MC. Both arrays (array A and array B) are positioned in the hand knob area, approximately 1 cm apart from each other. b, The participant is instructed to attempt handwriting under video guidance (Supplementary Video 1). c, Trial design schematic. Each trial consists of a single character displayed on the screen. A trial begins with the target character being displayed on the screen (prepare), followed by a go cue (green light), and acted writing of the character stroke by stroke (Methods). d, Writing of an example Chinese character in terms of strokes (top). e–g, Summary of the main findings. MC programmes character writing by sequencing a small set of stable states (f), each encoding a set of specific stroke fragments (e). A set of neurons exhibits directional tuning that is stable within each state but strongly variable across states (g). h, Writing movements were decoded using both state-dependent (first identifying the neural state and then performing state-dependent decoding for each fragment) and state-independent neural decoders Source data.

Source data

Results

Evidence of state-dependent encoding during handwriting

The participant performed attempted handwriting Chinese characters while observing virtual handwriting in the video (Fig. 1a–c, Supplementary Fig. 1a–c and Supplementary Video 1). We recorded 2,850 neurons across 20 experimental sessions (Supplementary Text), and each character was written 3 times. We first analysed whether some neurons reliably responded during the writing of individual characters using the Fisher’s discriminant value (FD), which was higher if a neuron generated similar responses when writing the same character twice than when writing two different characters (Fig. 2a and Supplementary Text). A number of neurons showed FD much higher than the chance level, that is, 1.0 ± 0.05 (M ± s.d., estimated by shuffling the responses across characters), demonstrating reliable responses during character writing. We next analysed whether the reliable neural responses to characters could be explained by the classic velocity-based directional tuning model^8,9,15. The reliability of neural response to individual characters, quantified by the FD, only had a moderate correlation with neural sensitivity to velocity direction, quantified by the R² of the directional tuning model (R = 0.46). In other words, neuronal tuning to velocity direction could not well explain neural responses to characters. In the following, to facilitate discussion, we loosely defined two categories of neurons: neurons not well explained by the directional tuning model were referred to as the complex-tuning neurons (n = 115 under the criterion that R² < 0.1 and FD ≥ 1.4, shown in blue in Fig. 2a), and neurons well explained by the directional tuning model were referred to as simple-tuning neurons (n = 64 under the criterion that R² ≥ 0.1 and FD ≥ 1.4, shown in magenta in Fig. 2a).

Fig. 2: Evidence of state-dependent encoding during handwriting.

a, Reliability and tuning property of neurons (n = 2,850 neurons across 20 sessions). The reliability of the response to each character is characterized using the Fisher’s discriminant value (FD) across characters (the 30 within each session), while the tuning property is characterized using the R² of the directional tuning model. Neurons with reliable tuning but cannot be explained by the directional tuning model are referred to as complex-tuning neurons (n = 115, R² < 0.1 and FD ≥ 1.4), and neurons conformed to the directional tuning model are referred to as simple-tuning neurons (n = 64, R² ≥ 0.1 and FD ≥ 1.4). b,c, Responses of exemplary complex-tuning neurons during handwriting, including the tuning curves (solid line, mean over 90 trials; shaded area, s.d.) and the neural firing rate overlaid on the character trajectory. b, An exemplary neuron that shows diverged responses to the same downward movement in two characters. c, An exemplary neuron that responds to multiple movement directions but does not consistently respond to any direction. d, Responses of exemplary simple-tuning neurons during handwriting, including the tuning curves (solid line, mean over 90 trials; shaded area, s.d.) and the neural firing rate overlaid on the character trajectory. The neuron responds to the downward direction during writing, while it responds to some fragments but not others, although the fragments contain similar trajectories Source data.

Source data

To analyse why the directional tuning model failed to perfectly predict the neuronal firing during character writing (as is evidenced by the relatively low R² of the model), we illustrated the firing pattern of example neurons by overlaying the neural firing rate during writing on the character trajectory. We observed two general phenomena that were illustrated by two example neurons. First, some neurons reliably responded during the writing of a small fragment of a character, but did not respond during the writing of other fragments that involved movements in the same direction. For example, the same downward vertical movement was involved when writing two characters, that is, ‘干’ and ‘于’, with highly similar orthographical forms but different pronunciations and meanings. A complex-tuning neuron, however, responded differently during the same continuous downward movement in the two characters: it responded to the movement for ‘于’ but did not respond for ‘干’ (Fig. 2b).

Second, some neurons responded to different movement directions in different character fragments. For example, the same neuron may respond to leftward (for example, stroke 1 in ‘手’), rightward (for example, stroke 2 in ‘手’) and downward (for example, first portion of stroke 4 in ‘写’) movements when writing some fragments of a character (Fig. 2c), but do not respond to the same movement directions when writing other fragments (for example, first portion of stroke 2 in ‘写’ for rightward movement, first portion of stroke 4 in ‘手’ for downward movement). Even for simple-tuning neurons, we observed that, although strong firing was mainly observed for a certain movement direction, the neuron may or may not fire when the movement direction appears (Fig. 2d). In other words, the neuron was tuned to a movement direction but its response gain seemed to be modulated during the writing process. Therefore, the directional tuning model only explained part of the neuronal activity of simple-tuning neurons (see Supplementary Fig. 2a,b for more examples).

Identification of stable states

Our previous analyses showed that the directional tuning of the neuron might change when writing different fragments. On the basis of these findings, we hypothesized that the writing of a character was decomposed into a sequence of stable states. Motor cortical neurons have stable directional tuning within each state, while they could have different preferred directions in different states.

To identify the stable states, we developed an algorithm, termed temporal functional clustering (TFC; Fig. 3a and Methods), which grouped the movement tuning function in each time bin (50 ms in duration) into a few clusters under a temporal continuity constraint (see Supplementary Fig. 3a,b for verification of the algorithm). A hyperparameter of the model was how many states were allowed. When only one state was allowed, the model was reduced to the classic directional tuning model, and the model complexity increased when the number of states increased.

Fig. 3: Identifying the stable states during handwriting.

a, Neural activity recorded during attempted handwriting is divided into non-overlapped stable states, which are classified using the TFC algorithm. Each colour denotes a specific state. b,c, The model encoding loss decreases when more states are included, and the tipping point occurs around 10 states. A total of 18 sessions, each containing 30 characters, were included (threefold cross-validation, each fold containing 10 characters with 3 repetitions, with non-overlapped characters across folds, M ± s.d.). Both the encoding loss (b) and the loss decrease (c) are given (n = 54, 18 sessions each containing 3 folds). d, With a threshold of loss decrease <10⁻⁵, we found that the mean number of states was around 10 (mean = 9.732, n = 54). e, Evaluation with the Bayesian information criterion (BIC) also indicated an optimal model number around 10 (the lowest mean BIC was obtained at the state number of 12 and 8 for training and test data, respectively, n = 54, M ± s.d.). f, Pairwise neural activity encoding loss between states. Each matrix entry (i, j) indicates the prediction error of neural activity in state j for the model trained on state i. A model can only well predict the neural responses during the state it is trained on. g, Visualization of encoding models learned by TFC with three non-overlapping character sets. The first two principal components of the linear mapping matrix were plotted. The encoding functions were mostly similar despite different character sets. h, State prediction performance of diverse kinematic parameters and neurons. Neural signals can reliably predict the states while kinematic parameters cannot (threefold cross-validation with no overlapping characters, chance level = 0.1). All box plots depict the median (horizontal line inside the box), 25th and 75th percentiles (boxes), and minimum and maximum values (whiskers) Source data.

Source data

We found that a small number of states was enough to significantly better predict the neural response than the baseline tuning curve model (P < 0.001 for any state number ≥2, one state versus two states, paired two-tailed t-test, t(107) = 52.36, P < 0.001, Cohen’s d = 0.709; Fig. 3b). To determine the optimal number of states, we performed threefold validation for data in each session, where each fold contained 10 distinct Chinese characters that were written 3 times and different folds did not have overlapping characters. The encoding loss on test set converged (decrease of loss <10⁻⁵) when about 10 states were modelled (Fig. 3b,c), and the result was consistent across all 18 sessions (Fig. 3d). Bayesian information criterion also indicated that an optimal number of states was around 10 (Fig. 3e). Notably, the number of states used here was much smaller than the number of Chinese characters (n = 306) and even the types of stroke for Chinese characters (n = 32).

When 10 states were used to model neuronal firing during writing, we found that the directional tuning models learned from one state could well explain neural activity during that state but not other states (Fig. 3f), and the state-dependent tuning models are mostly stable over different character sets (Fig. 3g). In our state-identification process, we clustered the mapping between neural activity and movement directions. Critically, we found that the state information can be also directly decoded from the activation pattern of the neural population but cannot be decoded from kinematic features. These results indicated that the stable states reflect characteristics of the MC, instead of the characteristics of movement features per se (Fig. 3h).

The state-dependent model decomposed the writing process into a sequence of states, with each state encoding multiple fragments that were part of a stroke (stroke fragments, with an average length of 198.4 ± 146.9 ms per fragment; Supplementary Fig. 3c). We observed that a character was decomposed into a similar state sequence in multiple trials (Supplementary Fig. 2c). Consistent results were observed when writing different contents, including English letters, shapes and numbers (Supplementary Fig. 2c). We further found that the state transfer process contained reliable patterns, that is, some states were more likely to appear after others, and was consistent across different character sets (Supplementary Fig. 3d,e). We further observed that the state sequences were associated with specific strokes, regardless of the Chinese character in which the stroke appeared (Supplementary Fig. 3f). This suggests that the state sequence is related to the more abstract meaning of writing, and not just to the movements of writing.

State-dependent tuning of handwriting

The state-dependent model better explained the neural responses of individual neurons than the classic directional tuning model (paired two-tailed t-test, t(156) = 14.66, P < 0.001, Cohen’s d = 1.265, threefold cross-validation with no overlapping characters across folds; Fig. 4a), for both simple-tuning neurons (Fig. 4b) and complex-tuning neurons (Fig. 4c). For complex-tuning neurons, the mean R² increased from 0.03 to 0.23 (paired two-tailed t-test, t(91) = 11.02, P < 0.001, Cohen’s d = 1.527, 95% confidence interval for the difference in mean R² (0.17, 0.24)). The state-dependent model also better explained the neuronal activities when writing English letters, shapes and numbers (Supplementary Fig. 4). In the following, we explored why the state-dependent model improved the modelling of simple- and complex-tuning neurons.

Fig. 4: State-dependent encoding model better predicts neuronal activities.

a–c, R² of the model that explains neural activity using state-dependent directional tuning (with neurons across 20 sessions, M ± s.d.). The state-dependent directional tuning model significantly enhances the R² for neurons (n = 157) with reliably tuning to characters, and the mean R² increased from 0.0873 to 0.2873 (state-dependent versus random states, paired two-tailed t-test, t(156) = 13.94, P = 3.37 × 10⁻²⁹, Cohen’s d = 1.092; state-dependent versus state-independent, paired two-tailed t-test, t(156) = 14.66, P = 3.897 × 10⁻³¹, Cohen’s d = 1.265) (a). For simple-tuning neurons (n = 65), the mean R² increased from 0.1748 to 0.3715 (state-dependent versus random states, paired two-tailed t-test, t(64) = 8.799, P = 1.271 × 10⁻¹², Cohen’s d = 1.086; state-dependent versus state-independent, paired two-tailed t-test, t(64) = 9.622, P = 4.716 × 10⁻¹⁴, Cohen’s d = 1.291) (b). For complex-tuning neurons (n = 92), the mean R² increased from 0.0254 to 0.2279 (state-dependent versus random states, paired two-tailed t-test, t(91) = 10.77, P = 6.226 × 10⁻¹⁸, Cohen’s d = 1.353; state-dependent versus state-independent, paired two-tailed t-test, t(91) = 11.02, P = 1.904 × 10⁻¹⁸, Cohen’s d = 1.527) (c) Source data.

Source data

We first examine the directional tuning behaviour of neurons across states. For each neuron, the state-dependent model estimated a directional tuning curve per state, and we illustrated these tuning curves for both simple- and complex-tuning models (Fig. 5a for normalized neural responses against directions of all neurons and Fig. 5b,c for tuning curves of representative neurons). For simple-tuning but not complex-tuning neurons, the tuning had similar preferred directions across different states (Fig. 5a,b). To quantify this effect, we analysed the preferred direction of each tuning curve (PD, representing the direction with the largest firing rates) and the standard deviation of PD was higher for complex-tuning than simple-tuning neurons (unpaired two-tailed Kolmogorov–Smirnov test, D(64,115) = 0.628, P < 0.001; Fig. 5d). Next, we further analysed the modulation depth of each tuning curve (MD, defined as the peak-to-peak value of the directional tuning curve). It was found that the MD varied across states even for simple neurons and the standard deviation of MD was comparable for complex- and simple-tuning neurons (unpaired two-tailed Kolmogorov–Smirnov test, D(64,115) = 0.200, P = 0.063; Fig. 5e). The state-dependent MD could explain why the state-dependent model outperformed the state-independent model even for simple-tuning neurons.

Fig. 5: State-dependent directional tuning of MC neurons.

a, Normalized firing rates over directions with both simple- and complex-tuning neurons, sorted based on state 1. The simple-tuning neurons show more consistent directional tuning over states compared with the complex-tuning neurons. b, Directional tuning curve of two exemplar simple-tuning neurons estimated using a state-independent model (black) or a state-dependent model (magenta). For the state-dependent model, a tuning curve is estimated based on each state and the tuning curves have a consistent preferred direction (PD) across states but the modulation depth (MD) varies across states. Darker colour for curves with higher R². c, Similar to b, but for complex-tuning neurons that exhibit variable directional tuning under different states. d,e, Statistical analysis of PD (d) and MD (e) for simple- and complex-tuning neurons. The standard deviation of PD is significantly higher for complex-tuning neurons (mean = 0.57, n = 115) than simple-tuning neurons (mean = 0.30, n = 64) (unpaired two-tailed Kolmogorov–Smirnov test, D(64,115) = 0.628, P = 1.97 × 10⁻²⁰ (d); unpaired two-tailed Kolmogorov–Smirnov test, D(64,115) = 0.200, P = 0.063 (e)) Source data.

Source data

Handwriting decoding based on stable states

The previous analyses demonstrated how individual neurons encode the handwriting process, and in the following, we utilized the population response to decode the handwriting trajectory. We built a state-dependent neural decoder to decode the movement velocity vector (direction with speed) and recovered the trajectory of each stroke based on velocity (Fig. 6a). To enable state-dependent decoding, we extended the velocity Kalman filter with a dynamic observation function (the linear mapping from kinematics to neural signals)¹⁴. Specifically, instead of using a static observation function, the state-dependent decoder contained a pool of observation models (which are the linear directional tuning models learned by TFC), and adaptively weighed and assembled the models based on the Bayesian inference of states, given the incoming neural signals.

Fig. 6: State-dependent decoding model improves the performance of handwriting trajectory prediction.

a, Diagrammatic representation of the state-dependent decoding process during handwriting (DyEnsemble). Utilizing encoding models for each state established through TFC, DyEnsemble dynamically infers the state and adaptively assembles a state-specific decoder in real time based on the incoming neural signals. This approach allows for adaptive switching between decoding models along with state switches. b, The writing trajectory was decoded using state-dependent and state-independent neural decoders. c,d, Performance of handwriting decoding using RMSE and R² between the ground truth trajectory and the decoded trajectory (offline evaluation with threefold cross-validation with no overlapping characters across folds in each session, n = 18; paired two-tailed t-test, t(17) = 31.20, P = 1.896 × 10⁻¹⁶, Cohen’s d = 2.199 (c); paired two-tailed t-test, t(17) = 31.37, P = 1.734 × 10⁻¹⁶, Cohen’s d = 2.495 (d)). All box plots depict the median (horizontal line inside the box), 25th and 75th percentiles (boxes), and minimum and maximum values (whiskers) Source data.

Source data

The state inferred by the state-dependent neural decoder was generally consistent with the state inferred by the neural encoding model (Supplementary Fig. 5a,b). Compared with a state-independent neural decoder (velocity Kalman filter⁹), the state-dependent decoder could decode handwriting with lower root mean squared error (RMSE; 13–18% decrease, paired two-tailed t-test, t(17) = 31.20, P < 0.001, Cohen’s d = 2.199; Fig. 6b,c) and higher R² (>69% increase, paired two-tailed t-test, t(17) = 31.37, P < 0.001, Cohen’s d = 2.495, Fig. 6b,d, threefold cross-validation with no overlapping characters across folds). Consistent results were obtained with both single-unit neural activity (SUA, offline sorted) and multi-unit neural activity (MUA, unsorted; Supplementary Fig. 5c). Significant improvement was also achieved when writing different contents, including English letters, shapes and numbers (Supplementary Fig. 6). Overall, these results confirmed that the state-dependent approach enhanced the decoding of stroke fragment trajectories during handwriting.

The decoding process could be achieved online, allowing the participant to use a robotic arm to write recognizable Chinese characters through attempted writing (Supplementary Video 2; the strokes were decoded by the state-dependent decoder, while the end of the strokes and the beginning of the next strokes were predefined to reconstruct the character from the strokes). We further evaluated the long-term reliability of handwriting decoding and found that the same state-dependent decoder could perform stably for a month (Supplementary Fig. 5d). Furthermore, its performance generalized to new characters (Supplementary Fig. 5d). Taken together, these results demonstrated that complex handwriting is decomposed into smaller units that are encoded in different neural states in the MC, and only within each state is movement encoded in a roughly linear manner.

Discussion

Handwriting is a highly sophisticated skilled behaviour that is special to the human being, and the inherent complexity of the Chinese writing task provides a unique window to dissect the underlying neural mechanisms for sophisticated fine movements. Through the task, we found that the human MC encodes a sophisticated writing process with a sequence of stable states, involving two types of neuron: (1) simple-tuning neurons that have stable directional tuning and (2) complex-tuning neurons that have variable directional tuning across states.

These results support a hierarchical control scheme of sophisticated movements (Supplementary Fig. 7): hypothetically, a highly complex movement trajectory is first decomposed into small and simple fragments, and each trajectory fragment is further converted into a sequence of movement velocities under a specific state of the MC. Furthermore, in this process, it is possible that (1) the complex-tuning neurons are upstream motor neurons related to the encoding of trajectory fragments, and (2) the simple-tuning neurons are downstream motor neurons related to the encoding of movement velocity. In other words, the complex-tuning neurons decompose a trajectory fragment into momentary velocity, and the movement velocity is implemented by the simple-tuning neurons. This two-step movement control perspective is in sharp contrast with the traditional perspective that the MC only carries out simple motor commands^7,16,17.

Hierarchically decomposing a complex sequence into smaller units is a common strategy in the brain⁵ and its neural underpinnings have been studied across multiple domains such as motor planning³, decision-making¹⁸, working memory¹⁹, song sequencing²⁰ and language processing²¹. Revealing the primitive units to decompose a sequence, however, turns out to be highly challenging, especially for a language-related process^6,22. On the basis of the writing behaviour, where the movements are associated with abstract meanings, characters and strokes are apparent candidates for the primitive unit for writing. Nevertheless, Chinese has a large number of characters (>3,500 frequent characters), and assigning a specific neural population for the writing of each character, that is, one-hot coding, is implausible. The number of stroke types is limited (n = 32). Nevertheless, strokes can be sophisticated, such as ‘’ and ‘’, and redundant, that is, sharing common elements such as vertical or horizontal movements. Furthermore, even the writing of a simple stroke such as ‘一’ can be meaningfully divided into a start, a body and an end, which are especially emphasized in Chinese calligraphy and correspond to the decomposition of a movement into acceleration and deceleration phases²³. Here we demonstrate that, in the MC, the writing of a character is decomposed into a sequence of states that correspond to fragments of a stroke. We also found that the state sequence was related to the strokes being written, which is the abstract meaning of writing rather than the movement parameters. This suggested that cognitive information was involved during handwriting encoding: state signals may originate from cognitive processes, while the MC receives the signals and performs state-dependent tuning during handwriting control.

Previous studies have demonstrated that neurons in the MC are tuned to movement features^{7,8,11,24,25,26} but static tuning to movement features has limited ability to explain the variance of neuronal activity^13,23,27, especially during natural movements²⁸. Instead, neural tuning to movement features can actively adapt to a specific task or environmental setting^29,30. In other words, depending on the external environment or instruction, the MC neurons can encode movements through different neural encoding subspaces^31,32,33. The current study, however, demonstrates intrinsic alternation between MC neural encoding subspace, depending on internally generated states during sophisticated movements. Similar ideas have also been proposed based on relatively simple movements, for example, decomposing a reaching movement into an acceleration phase and a deceleration phase^13,23,34,35, stereotyped movement fragments¹², but here we demonstrated many diverse states, which can encode various movement fragments using under a linear directional tuning model, and suggested a hierarchical model for the neural control of sophisticated movements. We further found that state transition occurred at the neural population level, supporting recent findings on population-level dynamics in MC^36,37.

A limitation of this study is that the results shown are from only one participant, and an important next step is to validate the results with more individuals. Second, in the experimental paradigm, the participant not only performed attempted handwriting but was simultaneously observing the virtual handwriting of the character. Thus, the neural signals could also contain the modulation of the observation process^38,39. Third, the proof-of-concept demonstration is still an open-loop control as the participant was watching the virtual hand in the video instead of the robotic arm writing the strokes (Supplementary Video 2). Further advances in decoders and systems are required to enable high-performance handwriting BCIs in a closed-loop manner. In addition, previous studies also identified primitive units in movements based on kinematic parameters^40,41,42,43 or muscle activities^{44,45,46,47,48}, indicating a hierarchical movement segmentation at different levels. The relationship between segmentations with different signals can be valuable for future work.

In summary, our results strongly demonstrate that sophisticated fine movements such as handwriting are encoded in the human MC as a sequence of stable states, each encoding a fragment of the movement, and the state-dependent encoding mechanism can shed light on future design of brain-computer interfaces for sophisticated fine movements.

Methods

Experimental model and subject details

Participant and ethics

All clinical and experimental procedures conducted in this study received approval from the Medical Ethics Committee of The Second Affiliated Hospital of Zhejiang University (ethical review number 2019-158, approved on 22 May 2019) and were registered in the Chinese Clinical Trial Registry (ref. ChiCTR2100050705). Informed consent was obtained verbally from the participant, along with the consent of his family members, and was duly signed by his legal representative. This study used an observational design and no intervention took place that was not driven by clinical need.

The volunteer participant is a right-handed man, 75 years old at the time of data collection. He was involved in a car accident and suffered from complete tetraplegia subsequent to a traumatic cervical spine injury at the C4 level, which occurred approximately 2 years before study enrolment. The volunteer participant demonstrated the ability to move body parts above the neck and exhibited normal linguistic competence and comprehension for all tasks. He scored 0/5 on skeletal muscle strength for limb motor behaviour.

On 27 August 2019, two 96-channel intracortical microelectrode arrays (4 mm × 4 mm Utah array with 1.5 mm length, Blackrock Microsystems) were implanted in the left MC, with one array located in the middle of the hand knob area (array A) and the other array located medially approximately 1 cm apart (array B), guided by structural (CT) and functional imaging (fMRI)⁴⁹. The participant was asked to perform imagery movement of hand grasping and elbow flexion/extension with fMRI scanning to confirm the activation area of the MC⁴⁹. Data presented in this study cover the period from post-implant days 1,374 to 1,792.

Method details

Neural signal recording and processing

Neural signals were recorded from the microelectrode arrays using the Neuroport system (NSP, Blackrock Microsystems). The signals were amplified, digitized and recorded at a sampling rate of 30 kHz. To reduce common mode noise, a common average reference filter was applied, subtracting the average signal across the array from each electrode. A digital high-pass filter with a cut-off frequency of 250 Hz was then applied to each electrode. Then, threshold crossing detection was performed using the Central software suite (Blackrock Microsystems). The threshold was set based on the root mean square (RMS) of the voltage time series recorded on each electrode. Specifically, thresholds ranging from −6.25 × RMS to −5.5 × RMS were used.

To analyse the neuronal activity, neurons were manually sorted with either Plexon Offline Spike Sorter v4 (offline analysis) or Central software (online decoding). After spike sorting, neuronal spikes were binned into 50 ms bins, without overlapping (each stroke contains 12 ± 6 bins, and each character contains 126 ± 24 bins). For the decoding tasks, the spike data were smoothed using an average filter of 5 bins.

The delay between the start of data extraction and the go cue was determined by evaluating a set of delay values ranging from −1,000 ms to 1,000 ms. The delay value of 300 ms was selected according to the overall decoding performance with a linear model.

Experimental paradigm

The participant performed an attempted handwriting task while observing a virtual handwriting of the character. During the experimental sessions, the participant attempted the handwriting of characters guided by instructional videos (Fig. 1 and Supplementary Video 1). The instructional video presented a virtual hand writing a target character stroke by stroke; at the same time, the participant attempted writing the character as if the virtual hand belonged to him.

For the Chinese character writing task, there were two paradigms.

• 1. Single-character writing with visual guidance (CW): a single Chinese character in dark green colour was displayed on the screen above a red square during the delay period, which lasted between 1 s and 3 s. After the delay period, the red square cue turned green and played a sound ‘ding’ to signal the participant to start writing. Simultaneously, a virtual hand holding chalk appeared on the screen and wrote the character stroke by stroke, highlighting the written part in bright green. The duration of the writing period varied depending on the complexity of the Chinese character, with more strokes requiring a longer writing time. After completing one character, the screen turned black and lasted for 1.5 s (Supplementary Video 1).

• 2. Sentence writing with visual guidance (SW): initially, the characters of a sentence were displayed in dark green on the screen above a red square. Following a delay period, the red square turned green, indicating the start of the sentence. The experimental procedure for each character within the sentence was identical to the visual guidance paradigm, with a short horizontal line appearing below the character as a reminder for the participant to begin writing a character (Supplementary Video 2).

The instructional video presents the writing process in a stroke-by-stroke manner. To facilitate smooth tracking, the velocity of the virtual hand was programmed to maintain a constant acceleration, ensuring ease of following for the participant.

The ‘single-character writing with visual guidance’ paradigm was used for data collection and offline analysis. The ‘sentence writing with visual guidance’ was mostly for online evaluation and demonstration. The main results were analysed offline, and the signal processing and analysis systems were developed by MATLAB and Python. For the online evaluation, the neural signal processing programme was developed in MATLAB, and the graphical user interface of the experimental task was developed in Python (see Supplementary Text for online settings).

TFC algorithm

The TFC algorithm is a computational approach designed to identify stable state and state switches during writing. The underlying assumption of TFC is that the neuronal encoding model, at the population level, may shift under different states while keeping stable within the same state. Under this assumption, TFC can automatically compute the neural mapping model for each state and detect state switches in a data-driven way.

Given a paired dataset $\left\{X,Y\,\right\}\equiv \left\{{x}_{1},\ldots ,{x}_{T},{y}_{1},\ldots ,{y}_{T}\right\}$, where $X\in {{\mathbb{R}}}^{{d}_{x}\times T}$ represents the writing kinematic data, and $Y\in {{\mathbb{R}}}^{{d}_{y}\times T}$ represents the preprocessed neural data, with d_x and d_y denoting the respective dimensions, and T representing the length of time bins. Our objective is to learn M encoding models of ${{\mathcal{H}}}_{m}\left(\bullet \right)\in \left\{{{\mathcal{H}}}_{1}\left(\bullet \right),{{\mathcal{H}}}_{2}\left(\bullet \right),\ldots ,{{\mathcal{H}}}_{M}\left(\bullet \right)\right\}$, where each model represents an encoding in a single state. In this study, each encoding model is a linear mapping from the velocity vector to the neural signals, that is, the velocity-based directional tuning model.

To obtain the M encoding models, TFC first randomly selected a set of encoding models and then applied the models to each data pair. The data would be assigned to the encoding model with minimal errors, and the models would update with the data assigned to them. The process repeated until the errors were minimized.

Specifically, the TFC algorithm uses an Expectation-Maximum (EM) process. Initially, we randomly set the parameters of M encoding models. Then we perform the Expectation-step (E-step), where each pair of {X,Y} is assigned to a specific encoding model where the data has the lowest encoding loss. Especially, the encoding loss is smoothed temporally to encourage that the adjacent data pair should belong to the same state (temporal constraint). After that, we perform the Maximum-step (M-step), where each model updates its parameters with the data pairs assigned to it. The TFC algorithm repeats the E-step and M-step iteratively until convergence.

• 1. Initialization step

  To obtain M initial models, we randomly set the parameters of each model ${{\mathcal{H}}}_{m}\left(\bullet \right)$. Each model is an encoding function that maps kinematics to neural signal estimation $\hat{Y}$:

  $${\hat{Y}}={{\mathcal{H}}}_{m}\left(X\,\right).$$

  (1)

• 2. E-step: data assignment

  The E-step aims to reassign data pairs to their fittest models. For each data pair $\left\{X,Y\,\right\}$, we can compute the predicted neural signal ${\hat{Y}}_{m}$ given kinematics $X$ and encoding model ${{\mathcal{H}}}_{m}\left({{\cdot }}\right)$:

  $${\hat{Y}}_{m}={{\mathcal{H}}}_{m}\left(X\,\right)$$

  (2)

  where ${\hat{Y}}_{m}\in {{\mathbb{R}}}^{{d}_{y}\times T}$ denotes the neural signals predicted by the encoding model ${{\mathcal{H}}}_{m}\left({{\cdot }}\right)$ for all the kinematics $\,X$. Given a set of $M$ encoding models, we can obtain $M$ predictions for each data pair. Then we calculate the encoding loss at each time step for each encoding model:

  $${E}_{m}=\sum \sqrt{{{||Y}-{\hat{Y}}_{m}{||}}^{2}}$$

  (3)

  where $\,{E}_{m}\in {{\mathbb{R}}}^{1\times {T}}$ is the encoding error between the neural signal ${\hat{Y}}_{{\rm{m}}}$ estimated by model ${{\mathcal{H}}}_{m}\left({{\cdot }}\right)$, and the ground truth $Y$, summed over all the neurons.

  Next, we smooth the error vector ${E}_{m}$ temporally to encourage data pairs that are adjacent in time to be assigned to the same model. With this constraint, we can obtain more temporally continuous state segmentation. The window size for a moving averaging smooth was typically set with 3 to 10 bins, denoted as ${l}_{{\rm{smooth}}}$. The smoothed encoding loss for model ${{\mathcal{H}}}_{m}\left({{\cdot }}\right)$ is given by

  $${E}_{m}={\rm{smooth}}\left({E}_{m},{l}_{{\rm{smooth}}}\right).$$

  (4)

  Practically, the parameter of ${l}_{{\rm{smooth}}}$ could affect the length of states, and a larger ${l}_{{\rm{smooth}}}$ usually leads to bigger lengths for states. Here we statistically analysed the length of states with different settings of ${l}_{{\rm{smooth}}}$. As shown in Supplementary Fig. 3c, the mean length of states was mostly around 200 ms across different settings.

  Once we have the smoothed encoding loss for each model, we assign each data pair to the model that gives the minimal encoding loss:

  $$E=\left[{E}_{1};{E}_{2};\ldots ;{E}_{m};\ldots ;{E}_{M}\right],$$

  (5)
  $${m}_{{\rm{assign}}}={{\rm{argmin}}}_{m}\left(E\right)$$

  (6)

  where $E\in {{\mathbb{R}}}^{M\times T}$ represents each model’s encoding loss and ${m}_{{\rm{assign}}}\in {{\mathbb{R}}}^{1\times T}$ denotes the model index selected.

• 3. M-step: parameter updating

  After the E-step, each data pair has been assigned to a specific model, and each model ${{\mathcal{H}}}_{m}\left({\rm{\cdot }}\right)$ has a collection of data pairs $\left\{{X}_{{{\mathcal{H}}}_{m}},{Y}_{{{\mathcal{H}}}_{m}}\right\}$. Then we can update the parameters for the models, by fitting the following function:

  $${Y}_{{{\mathcal{H}}}_{m}}={{\mathcal{H}}}_{m}\left({X}_{{{\mathcal{H}}}_{m}}\right)+{\epsilon }_{{{\mathcal{H}}}_{m}}$$

  (7)

  with ${\epsilon }_{{{\mathcal{H}}}_{m}}$ being the zero-Gaussian noise term. In this study, we use a linear function, such that ${{\mathcal{H}}}_{m}\left({\rm{\cdot }}\right)$ would include a linear mapping matrix and a Gaussian noise.

• 4. Repeat E-step and M-step until convergence

By iteratively performing the E-step and M-step, the overall encoding error will decrease continuously. Suppose at the ith iteration we have an error of e_i. One pre-set early-stopping threshold $\beta$ (typically set to 0.001) can be used to decide when to stop the iteration:

$${e}_{i} < \beta {e}_{i-1}.$$

(8)

When the iteration stops, the TFC algorithm will return the parameters for each model (that is, the directional tuning model) as well as the temporal segments corresponding to each model. The temporal segments indicate the segmentation of states.

Existing approaches, such as the hidden Markov model (HMM), can also segment movements into states²³. However, the HMM model only inputs neural signals, such that the temporal bins with similar neural signal patterns will be regarded as the same state. Meanwhile, TFC defines neural states as stable directional tuning between neural activities and movements, where temporal bins with similar tuning functions are regarded as the same state, and thus facilitate the state-dependent directional tuning model.

State-dependent neural decoder

A state-dependent neural decoder was proposed to allow dynamic switching of decoding models adaptively with changes in states (Fig. 6a). The state-space model of the Kalman filter includes two parts: a system function (mapping from previous kinematics to current kinematics) and an observation function (mapping from kinematics to neural signals). To enable state-dependent decoding, we extended the Kalman filter with a dynamic observation function, in a dynamic ensemble framework (DyEnsemble)¹⁴. The DyEnsemble uses the encoding models coming from the TFC algorithm as a pool of observation models and adaptively weighs and assembles the models based on the Bayesian rule, given the incoming neural signals. In this way, the DyEnsemble enables state-specific decoding that adapts to the change of states^14,50.

The DyEnsemble decoder defines the state-space model as follows:

$${x}_{k}=f\left({x}_{k-1}\right)+{\varsigma }_{k-1},$$

(9)

$${y}_{k}={h}_{k}\left({x}_{k}\right)+{\varepsilon }_{{\upsilon }_{k}}.$$

(10)

The model contains a system equation (equation (9)) that transmits the value of interest ${x}_{k-1}$ at time $k-1$ to the next time step $k$ using function $f(\bullet )$, with ${\varsigma }_{k} \sim N(0,{\sigma }_{\varsigma }^{2})$, a zero-mean Gaussian, being the transition noise. It also contains an observation equation (equation (10)), which uses ${x}_{k}$, to infer the measurement variable ${y}_{k}$ using function ${h}_{k}(\bullet )$, with a zero-mean Gaussian observation noise ${\varepsilon }_{{\upsilon }_{k}}$. Notably, the observation function ${h}_{k}(\bullet )$ is dependent on time, such that it dynamically changes over time. The DyEnsemble algorithm aims to estimate the dynamic measurement function (${h}_{k}(\bullet )$), and the corresponding ${x}_{k}$ over time, given the incoming neural signals (${y}_{k}$).

In the scenario of neural decoding, ${x}_{k}\in {{\mathbb{R}}}^{{d}_{x}}$ is the movement kinematics, and ${y}_{k}\in {{\mathbb{R}}}^{{d}_{y}}$ denotes the neural signals, with ${d}_{x}$ and ${d}_{y}$ denoting the respective dimensions. The observation function ${h}_{k}(\bullet )$ is an encoding function mapping from kinematics (${x}_{k}$) to neural signals (${y}_{k}$). DyEnsemble model maintains a pool of encoding models as $\left\{{{\mathcal{H}}}_{1}(\bullet ),{{\mathcal{H}}}_{2}(\bullet ),\ldots ,{{\mathcal{H}}}_{M}(\bullet )\right\}$. Given incoming neural signals ${y}_{k}$, DyEnsemble weighs the models in the pool by the Bayesian likelihood to ${y}_{k}$ and assembles ${h}_{k}(\bullet )$ in a Bayesian averaging rule. Here we have obtained the model pool with the TFC algorithm, with each model representing a specific state. Therefore, the DyEnsemble model can facilitate state-specific decoding by first inferring the state identity and then adaptively switching to the proper model.

Note that, if we consider a one-state condition, where the observation equation (equation (10)) uses a constant model instead of a state-dependent ${h}_{k}(\bullet )$, the equations can be solved with the Kalman filters for an optimal solution. Therefore, we used the Kalman filter as the state-independent decoder for comparison.

Specifically, considering a time series of neural signals ${y}_{0:k}$, the decoding problem involves estimating the kinematic state ${x}_{k}$ at time step $k$. The posterior distribution of the state can be specified by

$$p\left({x}_{k},|,{y}_{0:k}\right)=\mathop{\Sigma}\limits_{m=1}^{M}p\left({x}_{k},|,{h}_{k}\left({{\cdot }}\right)={{\mathcal{H}}}_{m}\left(\bullet \right),{y}_{0:k}\right)p\left({h}_{k}\left({{\cdot }}\right)={{\mathcal{H}}}_{m}\left(\bullet \right),|,{y}_{0:k}\right).$$

(11)

Here $p\left({x}_{k},|,{h}_{k}\left({{\cdot }}\right)={{\mathcal{H}}}_{m}(\bullet ),{y}_{0:k}\right)$ represents the kinematic state posterior estimated by the model ${{\mathcal{H}}}_{m}(\bullet )$ at time $k$, and $p\left({h}_{k}\left({{\cdot }}\right)={{\mathcal{H}}}_{m}(\bullet ),|,{y}_{0:k}\right)$ denotes the posterior probability of selecting the encoding model ${{\mathcal{H}}}_{m}(\bullet )$ at time $k$, which can be computed as follows:

$$p\left({h}_{k}\left({{\cdot }}\right)={{\mathcal{H}}}_{m}\left(\bullet \right),|,{y}_{0:k}\right)=\frac{p\left({h}_{k}\left({{\cdot }}\right)={{\mathcal{H}}}_{m}\left(\bullet \right),|,{y}_{0:k-1}\right){p}_{m}\left(\,{y}_{k},|,{y}_{0:k-1}\right)}{{\Sigma }_{j=1}^{M}p\left({h}_{k}\left({{\cdot }}\right)={{\mathcal{H}}}_{j}\left(\bullet \right),|,{y}_{0:k-1}\right){p}_{j}\left(\,{y}_{k}\left|\,{y}_{0:k-1}\right.\right)}$$

(12)

where $p\left({h}_{k}\left({\rm{\cdot }}\right)={{\mathcal{H}}}_{m}(\bullet ),|,{y}_{0:k-1}\right)$ represents the prior probability of choosing model ${{\mathcal{H}}}_{m}(\bullet )$ at time $k$, while ${p}_{m}\left(\,{y}_{k}\left|{y}_{0:k-1}\right.\right)$ is the marginal likelihood of choosing model ${{\mathcal{H}}}_{m}(\bullet )$ at time $k$. The marginal likelihood represents the confidence or reliability of a particular model’s prediction.

The prior probability at time $k$ can be recursively expressed as the posterior probability at time $k-1$, with a sticking factor $\alpha$:

$$p\left({h}_{k}\left({{\cdot }}\right)={{\mathcal{H}}}_{m}\left(\bullet \right)\left|\,{y}_{0:k-1}\right.\right)=\frac{{\left[p\left({h}_{k-1}\left({{\cdot }}\right)={{\mathcal{H}}}_{m}\left(\bullet \right),|,{y}_{0:k-1}\right)\right]}^{\alpha }}{{\sum }_{j=1}^{M}{\left[p\left({h}_{k-1}\left({{\cdot }}\right)={{\mathcal{H}}}_{j}\left(\bullet \right),|,{y}_{0:k-1}\right)\right]}^{2}}$$

(13)

where $p\left({h}_{k-1}\left({{\cdot }}\right)={{\mathcal{H}}}_{m}(\bullet ),|,{y}_{0:k-1}\right)$ is the posterior probability of choosing encoding model ${{\mathcal{H}}}_{m}(\bullet )$ at time $k-1$. The parameter $\alpha \in (0,1)$ represents the sticking factor, where a higher value leads to smoother changes in the model weights.

And the marginal likelihood can be computed as follows:

$${p}_{m}\left(\,{y}_{k},|,{y}_{0:k-1}\right)=\int {p}_{m}\left(\,{y}_{k},|,{x}_{k}\right)p\left({x}_{k},|,{y}_{0:k-1}\right)d{x}_{k}$$

(14)

where ${p}_{m}\left({y}_{k},|,{x}_{k}\right)$ is the likelihood of model ${{\mathcal{H}}}_{m}(\bullet )$ for a specific kinematic state ${x}_{k}$. The DyEnsemble model can be solved using a particle filtering algorithm (see Supplementary Text for details).

Statistical analysis

In Fig. 3b, we applied the paired t-test (two-tailed), the P < 4.417 × 10⁻⁷⁸ for any state number ≥2. In Fig. 4a–c, we applied the paired t-test (two-tailed), with n = 157, n = 65 and n = 92. The P values are 3.37 × 10⁻²⁹/3.897 × 10⁻³¹ (state-dependent versus random states/state-dependent versus state-independent), 1.271 × 10⁻¹²/4.716 × 10⁻¹⁴ and 6.226 × 10⁻¹⁸/1.904 × 10⁻¹⁸, respectively. In Fig. 5d,e, we applied the Kolmogorov–Smirnov test (two-tailed). For Fig. 5d, n = 64 and 115, with P = 1.97 × 10⁻²⁰. For Fig. 5e, n = 64 and 115, with P = 0.06299. In Fig. 6c,d, we applied the paired t-test (two-tailed), with n = 18 sessions. The P values are 1.896 × 10⁻¹⁶ and 1.734 × 10⁻¹⁶ for the RMSE and R², respectively. In Supplementary Fig. 3e, we applied a paired t-test (two-tailed) with n = 18 sessions. The P value is 1.373 × 10⁻¹². In Supplementary Fig. 4, we applied the paired t-test (two-tailed) with n = 157 reliable neurons. The P values for English letters, shapes and numbers are 2.098 × 10⁻⁷/1.642 × 10⁻⁸ (state-dependent versus random states/state-dependent versus state-independent), 2.556 × 10⁻⁵/1.133 × 10⁻⁶ and 5.77 × 10⁻⁷/5.865 × 10⁻⁹, respectively. In Supplementary Fig. 5c, we applied a paired t-test, with n = 18 sessions. The P values are 3.49 × 10⁻⁴ and 6.507 × 10⁻⁸ for state-independent and state-dependent. In Supplementary Fig. 6b, we applied a paired t-test (two-tailed). The P values are 3.385 × 10⁻¹⁴, 3.229 × 10⁻¹², 1.567 × 10⁻¹² and 6.614 × 10⁻¹⁰ for the characters, English letters, shapes and numbers, respectively.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.