Abstract
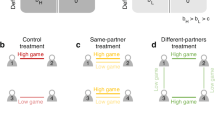
The awareness of individuals regarding their social network surroundings and their capacity to use social connections to their advantage are well-established human characteristics. Economic games, incorporated with network science, are frequently used to examine social behaviour. Traditionally, such game models and experiments artificially limit players’ abilities to take varied actions towards distinct social neighbours, thereby constraining their social networking agency. Here we designed an experimental paradigm that alters this agency and applied it to the prisoner’s dilemma (N = 735), trust game (N = 735) and ultimatum game (N = 735) to investigate cooperation, trust and fairness. Granting participants greater network agency led to more prosocial behaviour across all three economic games, resulting in higher wealth and lower inequality compared with control groups. These findings suggest that incorporating social networking agency into experimental designs better captures the prosocial potential of human behaviour.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The Open Science Framework page for this project (https://osf.io/n84dv/) includes all data from laboratory experiments.
Code availability
The codes for numerical analysis are available via the Open Science Framework at https://osf.io/n84dv/.
References
Boissevain, J. Friends of Friends: Networks, Manipulators and Coalitions (Basil Blackwell, 1974).
Watts, D. J., Dodds, P. S. & Newman, M. E. J. Identity and search in social networks. Science 296, 1302–1305 (2002).
Fowler, J. H. & Christakis, N. A. Social networks and cooperation in hunter-gatherers. Nature 481, 497–501 (2012).
Henrich, J. & Muthukrishna, M. The origins and psychology of human cooperation. Annu. Rev. Psychol. 72, 207–240 (2021).
Fehr, E. & Fischbacher, U. The nature of human altruism. Nature 425, 785–791 (2003).
Rand, D. G. & Nowak, M. A. Human cooperation. Trends Cogn. Sci. 17, 413–425 (2013).
Ohtsuki, H., Hauert, C., Lieberman, E. & Nowak, M. A. A simple rule for the evolution of cooperation on graphs and social networks. Nature 441, 502–505 (2006).
Santos, F. C., Santos, M. D. & Pacheco, J. M. Social diversity promotes the emergence of cooperation in public goods games. Nature 454, 213–216 (2008).
Fowler, J. H. & Christakis, N. A. Cooperative behavior cascades in human social networks. Proc. Natl Acad. Sci. USA 107, 5334–5338 (2010).
Szabó, G. & Fath, G. Evolutionary games on graphs. Phys. Rep. 446, 97–216 (2007).
Bliege Bird, R., Ready, E. & Power, E. A. The social significance of subtle signals. Nat. Hum. Behav. 2, 452–457 (2018).
Goyal, S. Networks: An Economics Approach (MIT Press, 2023).
Thielmann, I., Spadaro, G. & Balliet, D. Personality and prosocial behavior: a theoretical framework and meta-analysis. Psychol. Bull. 146, 30–90 (2020).
van Dijk, E. & De Dreu, C. K. W. Experimental games and social decision making. Annu. Rev. Psychol. 72, 415–438 (2021).
Rapoport, A., Chammah, A. M. & Orwant, C. J. Prisoner’s Dilemma: A Study in Conflict and Cooperation (Univ. Michigan Press, 1965).
Berg, J., Dickhaut, J. & McCabe, K. Trust, reciprocity, and social history. Games Econ. Behav. 10, 122–142 (1995).
Güth, W., Schmittberger, R. & Schwarze, B. An experimental analysis of ultimatum bargaining. J. Econ. Behav. Organ. 3, 367–388 (1982).
Camerer, C. F. Behavioral Game Theory: Experiments in Strategic Interaction (Princeton Univ. Press, 2011).
Kagel, J. H. & Roth, A. E. The Handbook of Experimental Economics 2 (Princeton Univ. Press, 2020).
Dal Bó, P. & Fréchette, G. R. The evolution of cooperation in infinitely repeated games: experimental evidence. Am. Econ. Rev. 101, 411–429 (2011).
Bó, P. D. Cooperation under the shadow of the future: experimental evidence from infinitely repeated games. Am. Econ. Rev. 95, 1591–1604 (2005).
Battiston, F. et al. Networks beyond pairwise interactions: structure and dynamics. Phys. Rep. 874, 1–92 (2020).
Jusup, M. et al. Social physics. Phys. Rep. 948, 1–148 (2022).
Gracia-Lázaro, C. et al. Heterogeneous networks do not promote cooperation when humans play a prisoner’s dilemma. Proc. Natl Acad. Sci. USA 109, 12922–12926 (2012).
Rand, D. G., Nowak, M. A., Fowler, J. H. & Christakis, N. A. Static network structure can stabilize human cooperation. Proc. Natl Acad. Sci. USA 111, 17093–17098 (2014).
Perc, M. & Szolnoki, A. Coevolutionary games—a mini review. BioSystems 99, 109–125 (2010).
Perc, M., Gómez-Gardenes, J., Szolnoki, A., Floría, L. M. & Moreno, Y. Evolutionary dynamics of group interactions on structured populations: a review. J. R. Soc. Interface 10, 20120997 (2013).
Fehl, K., van der Post, D. J. & Semmann, D. Co-evolution of behaviour and social network structure promotes human cooperation. Ecol. Lett. 14, 546–551 (2011).
Rand, D. G., Arbesman, S. & Christakis, N. A. Dynamic social networks promote cooperation in experiments with humans. Proc. Natl Acad. Sci. USA 108, 19193–19198 (2011).
Melamed, D., Harrell, A. & Simpson, B. Cooperation, clustering, and assortative mixing in dynamic networks. Proc. Natl Acad. Sci. USA 115, 951–956 (2018).
Su, Q., McAvoy, A. & Plotkin, J. B. Evolution of cooperation with contextualized behavior. Sci. Adv. 8, eabm6066 (2022).
Jia, D. et al. Evolutionary dynamics drives role specialization in a community of players. J. R. Soc. Interface 17, 20200174 (2020).
Su, Q., Li, A. & Wang, L. Evolution of cooperation with interactive identity and diversity. J. Theor. Biol. 442, 149–157 (2018).
McAvoy, A. & Hauert, C. Asymmetric evolutionary games. PLoS Comput. Biol. 11, e1004,349 (2015).
Su, Q., Allen, B. & Plotkin, J. B. Evolution of cooperation with asymmetric social interactions. Proc. Natl Acad. Sci. USA 119, e2113468118 (2022).
Hübner, V., Staab, M., Hilbe, C., Chatterjee, K. & Kleshnina, M. Efficiency and resilience of cooperation in asymmetric social dilemmas. Proc. Natl Acad. Sci. USA 121, e2315558121 (2024).
Peysakhovich, A., Nowak, M. A. & Rand, D. G. Humans display a ‘cooperative phenotype’ that is domain general and temporally stable. Nat. Commun. 5, 4939 (2014).
Poncela-Casasnovas, J. et al. Humans display a reduced set of consistent behavioral phenotypes in dyadic games. Sci. Adv. 2, e1600451 (2016).
Engle-Warnick, J. & Slonim, R. L. Learning to trust in indefinitely repeated games. Games Econ. Behav. 54, 95–114 (2006).
King-Casas, B. et al. The rupture and repair of cooperation in borderline personality disorder. Science 321, 806–810 (2008).
Güth, W. & Kocher, M. G. More than thirty years of ultimatum bargaining experiments: motives, variations, and a survey of the recent literature. J. Econ. Behav. Organ. 108, 396–409 (2014).
Han, X. et al. Emergence of communities and diversity in social networks. Proc. Natl Acad. Sci. USA 114, 2887–2891 (2017).
Cherry, T. L., Kroll, S. & Shogren, J. F. The impact of endowment heterogeneity and origin on public good contributions: evidence from the lab. J. Econ. Behav. Organ. 57, 357–365 (2005).
Nishi, A., Shirado, H., Rand, D. G. & Christakis, N. A. Inequality and visibility of wealth in experimental social networks. Nature 526, 426–429 (2015).
Hauser, O. P., Hilbe, C., Chatterjee, K. & Nowak, M. A. Social dilemmas among unequals. Nature 572, 524–527 (2019).
Camerer, C.F., Fehr, E. in Foundations of Human Sociality (eds. Henrich, J. et al.) 55–59 (Oxford Univ. Press, 2004).
Galesic, M. et al. Human social sensing is an untapped resource for computational social science. Nature 595, 214–222 (2021).
Balliet, D., Wu, J. & De Dreu, C. K. W. Ingroup favoritism in cooperation: a meta-analysis. Psychol. Bull. 140, 1556–1581 (2014).
Romano, A., Balliet, D., Yamagishi, T. & Liu, J. H. Parochial trust and cooperation across 17 societies. Proc. Natl Acad. Sci. USA 114, 12702–12707 (2017).
Sohn, Y., Choi, J. K. & Ahn, T. K. Core-periphery segregation in evolving prisoner’s dilemma networks. J. Complex Netw. 8, cnz021 (2019).
Almaatouq, A. et al. Scaling up experimental social, behavioral, and economic science. Preprint at https://doi.org/10.31219/osf.io/wksv8_v1 (2021).
Shi, L. et al. Freedom of choice adds value to public goods. Proc. Natl Acad. Sci. USA 30, 17,516–17,521 (2020).
Tomasello, M., Melis, A. P., Tennie, C., Wyman, E. & Herrmann, E. Two key steps in the evolution of human cooperation: the interdependence hypothesis. Curr. Anthropol. 53, 673–692 (2012).
Chen, D. L., Schonger, M. & Wickens, C. otree—an open-source platform for laboratory, online, and field experiments. J. Behav. Exp. Finance 9, 88–97 (2016).
Kim, D. G. Clustering Standard Errors at the ‘Session’ Level (CESifo, 2020).
Abadie, A., Athey, S., Imbens, G. W. & Wooldridge, J. M. When should you adjust standard errors for clustering? Q. J. Econ. 138, 1–35 (2023).
Charrad, M., Ghazzali, N., Boiteau, V. & Niknafs, A. NbClust: an R package for determining the relevant number of clusters in a data set. J. Stat. Softw. 61, 1–36 (2014).
Acknowledgements
We thank M. Jusup and Z. Bašić for helpful comments on both the experimental design and the article. We thank T. Li and X. Hu for technical assistance with the experimental platform. Z.W. was supported by the National Science Fund for Distinguished Young Scholars (grant no. 62025602), the National Natural Science Foundation of China (grant no. U22B2036) and the XPLORER PRIZE 2021 of the Tencent Foundation. I.R. was supported by JSPS KAKENHI (grant no. JP 24K16333). L.S. was supported by the Major Program of National Fund of Philosophy and Social Science of China (grant No. 22&ZD158). Q.S. was supported by the National Natural Science Foundation of China (grant no. 62473252) and the Shanghai Pujiang Program (grant no. 23PJ1405500). C.L. was supported by the National Natural Science Foundation of China (grant no. 62476221). J.L. was supported by the National Natural Science Foundation of China (grant no. 62366058). P.H. was supported by JSPS KAKENHI (grant no. JP 25K01452). The funders had no role in the study design, data collection and analysis, decision to publish or preparation of the paper.
Author information
Authors and Affiliations
Contributions
D.J., I.R. and Z.W. conceived the project. D.J. and I.R. designed the laboratory experiments. D.J. and Z.W. organized the experiments and collected the data, supported by L.S., C.L., J.L. and X.L. D.J. and I.R. analysed data with inputs from and Z.W. and P.H. D.J., I.R. and P.H. prepared the figures. Q.S. and D.J. developed the numerical model. I.R. wrote the paper with inputs from D.J. and Z.W., and revisions from P.H.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Human Behaviour thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 The second stage of the trust and ultimatum games follows a similar pattern as the first stage.
Despite the absence of distinction between constrained and free players in the second stage, an increase in the fraction of free players typically results in a rise in (a) the returned amount in the trust game and (b) the accepted amount in the ultimatum game. Each group consisted of three independent sessions with 49 participants per session (N = 147 per group). Each game comprised a control group with a population of constrained players and three treatments with mixed populations, including low, medium, and high fractions of free players, as well as a treatment with a population entirely composed of free players. Upper panels show individual data points, with boxes indicating the 25th and 75th percentiles and the space between the boxes marking the median. Lower panels display effect sizes and 98.75% confidence intervals. Statistical significance was evaluated using two-sided t-tests with the Bonferroni correction.
Extended Data Fig. 2 Cooperation, trust, and fairness surge when players are free to act differently with neighbours, often within the first round of the game.
The figure depicts the temporal evolution of six variables across three games, each dataset representing the average of three replicates. The average and the 95% confidence bands of a time series model fitted to the data are also displayed (Extended Data Tables 1 and 2). (a) In the prisoner’s dilemma, the cooperation frequency shows a downtrend in the control group, a slight downtrend in mixed population treatments, and a slight uptrend in the free-player population treatment. (b) In the trust game, the entrusted amount exhibits a slight downtrend in the control and treatments with low and high densities of free players but a slight uptrend in the treatment with a medium density of free players and in the free-player population treatment. The returned amount shows a slight downtrend across both the control and all treatments. (c) In the ultimatum game, the proposed, accepted, and rejected amounts show a downtrend in control and across all treatments.
Extended Data Fig. 3 Social networking agency increases wealth and decreases inequality.
Scatter plots display individual data points, and the error bars denote the group mean and standard error (SE). Each group consists of three independent sessions with 49 participants per session (N = 147 per group). (a-c) In the prisoner’s dilemma and trust game, wealth based on player type increases steadily as treatments permit more free players. In the ultimatum game, wealth differences are subtle. However, free players are wealthier across all mixed treatment groups, reflecting their ability to optimize strategies for each neighbour. (d-f) In the prisoner’s dilemma and trust game, inequality based on player type initially spikes in the second treatment, where free players are in the minority, and then gradually decreases to levels lower than in the initial treatment. In the ultimatum game, the situation is reversed. Inequality increases with the rising fraction of free players but drops when the population is entirely free, though with smaller variations in overall inequality levels. (g-h) Wealth disparities are more pronounced between stages of the game, as players in both games accrue most of their wealth in the second stage. While in the trust game, wealth consistently increases in both stages as the fraction of free players rises, in the ultimatum game, wealth in the proposer stage slightly decreases with a higher fraction of free players. (i-j) In the trust game, inequality based on game stage increases with a higher fraction of free players, reflecting the fact that more players in the population can optimize their strategies, leading to varying levels of success. In the ultimatum game, inequality increases in both stages, although overall inequality levels remain relatively similar.
Extended Data Fig. 4 Behavioural phenotypes in the second stage of the trust and ultimatum games mirror those in the first stage.
Using the six clustering factors from Fig. 3, we identify prosocial, neutral, and antisocial types in both stages of the games. a) In the second stage of the trust game, unlike the first stage where prosocial players predominate as the fraction of free players increases, neutral players become more prominent. The clustering factors represent average values in the current round for (A) the returned amount; (B) the returned amount after the trustee received four or more in the previous round; (C) the returned amount after the trustee received less than four in the previous round; and (D - F) the returned amount after up to one, exactly two, or at least three neighbouring trustors sent an amount equal to or greater than in the previous round; b) In the second stage of the ultimatum game, patterns resemble the first stage, with a relatively constant number of neutral players, but an increasing number of prosocial players and a decreasing number of antisocial players. The clustering factors represent average values in the current round for (A) the accepted amount; (B) the accepted amount after receiving a total offer of four or more in the previous round; (C) the accepted amount after receiving a total offer of less than four in the previous round; and (D - F) the accepted amount when up to two, exactly three, or exactly four neighbouring proposers propose an amount equal to or greater than in the previous round.
Extended Data Fig. 5 Player behaviour remains consistent across different stages of the trust and ultimatum games.
Applying the same clustering factors as in Extended Data Fig. 3 to the behavioural phenotypes derived from the first stage of games reveals a consistent pattern of behaviour in the second stage. Specifically, if a player adopts a prosocial, neutral, or antisocial role in the first stage of the trust and ultimatum game, they are likely to maintain the same behaviour in the second stage.
Extended Data Fig. 6 Trustors tend to increase the amounts they entrust in response to larger returns received in the previous round.
Each panel shows fitted regression lines with shaded bands representing 95% confidence intervals (CI). The presence of free players allows for more diverse strategies, observable in the spread of data points. This diversity is evident as some players opt to entrust less despite receiving more from neighbouring trustees in prior rounds. The regression slopes are 0.39 [95%CI: 0.30, 0.48], 0.58 [0.53, 0.63], 0.49 [0.44, 0.54], 0.35 [0.30, 0.39], and 0.33 with [0.28, 0.39], respectively. The intercepts are 0.25 [0.23, 0.28], 0.31 [0.28, 0.34], 0.43 [0.38, 0.47], 0.58 [0.52, 0.63], and 0.63 with [0.56, 0.71], respectively. The adjusted R2 values are 0.11 (F = 72.98, P < 10−15), 0.48 (F = 551.7, P < 10−15), 0.37 (F = 342.2, P < 10−15), 0.30 (F = 255.5, P < 10−15), and 0.19 (F = 140.1, P < 10−15), respectively.
Extended Data Fig. 7 Proposers tend to increase their offers in response to acceptance and rejection in the previous round.
Each panel shows fitted regression lines with shaded bands representing 95% confidence intervals (CI). The narrow data range in the low fraction of free players’ treatment suggests that proposers adhere to successful offer amounts. In treatments with a majority of free players, some proposers opt to offer less despite previous acceptance, indicating a willingness to test established relationships and adjust responder expectations. However, when offers are rejected, proposers tend to increase their subsequent offers, suggesting they learn from rejection and attempt to make offers more appealing. The steeper slope with higher densities of free players might suggest that in a freer population, proposers encounter a variety of responder thresholds for acceptance, prompting them to adjust their offers upward to find a successful compromise. In the case of acceptance, the regression slopes are 0.85 [95%CI: 0.81, 0.88], 0.99 [0.98, 1.01], 1.00 [0.99, 1.01], 0.98 [0.96, 0.99], and 0.99 [0.98, 1.01], respectively. The intercepts are 0.10 [0.07, 0.13], − 0.02[ − 0.03, − 0.01], − 0.03[ − 0.04, − 0.02], − 0.04[ − 0.06, − 0.02], and − 0.06[ − 0.09, − 0.04], respectively. The adjusted R2 values are 0.80 (F = 2320, P < 10−15), 0.97 (F = 2.11 × 104, P < 10−15), 0.98 (F = 2.74 × 104, P < 10−15), 0.95 (F = 1.14 × 104, P < 10−15), and 0.96 (F = 1.45 × 104, P < 10−15), respectively. In the case of rejection, the regression slopes are 0.09 [95%CI: 0.03, 0.15], 0.27 [0.19, 0.35], 0.58 [0.51, 0.66], 0.47 [0.36, 0.58], and 0.90 [0.80, 1.00], respectively. The intercepts are 0.71 with [0.68, 0.75], 0.59 with [0.55, 0.63], 0.42 with [0.38, 0.47], 0.47 with [0.42, 0.53], and 0.30 with [0.24, 0.37], respectively. The adjusted R2 values are 0.02 (F = 10.16, P < 0.01), 0.09 (F = 46.86, P < 10−10), 0.33 (F = 239, P < 10−15), 0.13 (F = 69.18, P < 10−15), and 0.39 (F = 311, P < 10−15), respectively.
Supplementary information
Supplementary Information
Supplementary experimental set-up details, analyses, cluster analysis and model analysis.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Jia, D., Romić, I., Shi, L. et al. Social networking agency and prosociality are inextricably linked in economic games. Nat Hum Behav (2025). https://doi.org/10.1038/s41562-025-02289-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41562-025-02289-0