Main

In mitosis, the chromosomes of eukaryotic cells undergo a dramatic metamorphosis as they are shaped into individualized, rod-like structures of very high density1. This remarkable transition is realized by the concerted action of several proteins, including condensin I and II, topoisomerase IIα and the chromokinesin KIF4A (ref. 1), leading to the formation of a central protein scaffold from which the chromatin fibre, composed of deoxyribonucleic acid (DNA) and histone complexes, emanates in radial loops2,3,4. Simultaneously, chromosomes are compacted by a factor of two5,6. Although the name ‘condensin’ suggests that these protein complexes are also responsible for chromosome condensation, rapid depletion of these proteins does not markedly impact chromosome density7. Instead, it has been shown that the density of mitotic chromosomes is controlled by post-translational modifications of histones, in particular through histone deacetylation8,9, and is strongly dependent on cations, including Ca2+ (ref. 10), Mg2+ (refs. 11,12,13) and polyamines13,14, because of the polyelectrolyte nature of the chromatin fibre15. Accordingly, polyamine and Mg2+ concentrations in the cell increase during mitosis12,16.

Chromosome condensation is followed by attachment of the chromosomes to the mitotic spindle, which segregates the two sister chromatids to the two daughter cells. This is a mechanical process that involves forces estimated to be at least tens of piconewtons17, indicating that the biological function of mitotic chromosomes depends on their mechanics18,19. These mechanical properties have been characterized with high precision, using micropipettes and optical tweezers20,21,22, revealing an intricate nonlinear and viscoelastic response to applied forces. However, the physical origin of these viscoelastic properties has remained elusive. Furthermore, it has recently been shown that chromosome condensation mediated by histone deacetylation is crucial for chromosomal stability9, leading to the question of how chromosome condensation, mechanics and biological function are related. A common and powerful approach for understanding the mechanics of polymer networks, such as mitotic chromosomes, is to characterize networks prepared at different concentrations or with different polymer modifications, and then use theoretical modelling to determine the underlying physical principles23,24,25. This approach is, however, not readily applicable to biomaterials such as mitotic chromosomes, as we have limited control over their composition.

Here we overcome this challenge by subjecting optically trapped mitotic chromosomes to two different in situ manipulations: ion-mediated chromosome condensation and high-salt depletion of histone complexes. We find that the stiffness and fluidity of mitotic chromosomes are highly responsive to ionic conditions. By analysing the changes in nonlinear chromosome mechanics upon manipulation, we demonstrate that chromatin in the mitotic chromosome behaves like a flexible polymer. We also characterize chromosomal fluidity and find that it can be explained by modelling the chromatin loops as an entangled polymer solution.

In situ chromosome manipulation

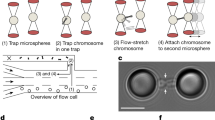
To enable the in situ manipulation of mitotic chromosomes, we used an optical tweezers set-up integrated with a multichannel microfluidic flow cell (Fig. 1a). This set-up enabled a chromosome to be attached between two optically trapped microbeads via the streptavidin–biotin interaction22, and then to rapidly and precisely change its physico-chemical environment by moving the optical traps with the chromosome to different channels. We then used the optical tweezers to probe the impact of changes in buffer conditions on the structure and mechanics of the trapped chromosome. With this approach, we do not control which one of the different chromosomes is trapped, thus introducing intrinsic variability between different measurements22. Therefore, it is crucial to directly compare the mechanics of the same chromosome before and after manipulation.

Fig. 1: Optical tweezers experiment to examine in situ ion-mediated chromosome condensation and histone depletion.
figure 1

a, Schematic of the experiment: the multichannel flow cell enabled us to maintain different ionic conditions and concentrations in the main channels 1–3 (where channel 1 also contains streptavidin-coated microbeads) on the one hand and in side channel 5 on the other hand. Chromosomes were introduced into the flow cell via channel 4. b, Illustration of the two manipulations carried out: reversible ion-mediated chromosome condensation (left) and irreversible depletion of histones (right). The contour length (green) and persistence length (yellow) are indicated in the right panel. c, Fluorescence images of eGFP-tagged H2B histones of a chromosome in the condensed (+ polyamines) and decondensed (− polyamines) states. Scale bar, 2 μm. d, Schematic illustrating the physics of ion-mediated chromosome condensation: the strong negative charge of chromatin needs to be compensated by counterions, leading to an osmotic pressure Π that drives water into the chromosome (top). When these counterions are replaced by polyamines, which act as more effective counterions, the chromosome condenses (bottom). e, Box plot of the relative length change of chromosomes from U2OS and HCT116 cells caused by polyamines, PEG and histone depletion. The box plot marks the quartiles of the distribution, the whiskers show the whole distribution and the centre line marks the median. To obtain a robust estimate of the size change, we compared the length of the chromosome at 50 pN, ℓ(50 pN), before and after changing the solvent conditions. For polyamines, we found a mean length ratio of 121 ± 5% (decondensed/condensed, mean ± standard error of the mean (s.e.m.), N = 25 chromosomes); for PEG, 143 ± 8% (N = 12 chromosomes); for histone depletion, 355 ± 66% (N = 10 chromosomes). f, Normalized length of chromosomes from U2OS cells at a constant force of 250 pN. Without polyamines or PEG, chromosomes frequently elongated stepwise and often disintegrated to the point where they could not support a force of 250 pN (red dots) (N = 7 chromosomes per condition).

Full size image

We applied two different manipulations: in addition to changing the ionic conditions to reversibly condense or decondense chromosomes26, we depleted histone complexes irreversibly by subjecting the chromosomes to high-salt conditions (Fig. 1b)2. For the first manipulation, we used the physiological short-chained polyamines spermidine3+ and spermine4+ (ref. 14) (Extended Data Fig. 1). When a chromosome was moved from polyamine-free buffer to a buffer supplemented with physiological concentrations of spermidine3+ (0.5 mM) and spermine4+ (0.2 mM), we observed an immediate decrease in chromosome size (and vice versa; Extended Data Fig. 2a), which was apparent in force–distance measurements and in bright-field images and fluorescence images of chromosomes containing histone H2B labelled with enhanced green fluorescent protein (H2B-eGFP) (Fig. 1c). These changes were mostly reversible when the chromosome was returned to the initial buffer. Whereas polyamine-induced compaction was rapid, decompaction upon depletion of polyamines took several minutes to complete, possibly due to polyamines only slowly detaching from DNA (Extended Data Fig. 2b–d)26.

Previous work has demonstrated that specific interactions between polyamines and DNA can lead to the formation of well-defined DNA–polyamine condensates27,28,29,30. To explain chromosome condensation by polyamines, however, it is not necessary to account for molecular details. Instead, chromosome condensation can be readily explained as the shrinking and swelling of a polyelectrolyte gel described by Donnan’s theory26,31: charges in the polyelectrolyte need to be compensated by counterions, leading to a concentration difference of these ions with the bulk of the solvent and an osmotic pressure that causes the gel to swell (Fig. 1d, top). Multivalent ions, such as polyamines, act as more efficient counterions: by replacing several monovalent cations, they reduce the osmotic pressure inside the chromosome, which in turn leads to shrinking of the polyelectrolyte gel, that is, chromosome condensation26,32 (Fig. 1d, bottom). The density of polyelectrolyte gels can change discontinuously with ion concentration, a phenomenon that is referred to as a volume phase transition26,33.

One prediction of Donnan’s theory is that chromosome swelling is ultimately driven by osmotic pressure and can therefore be counteracted by adding osmolytes, such as long-chained poly(ethylene glycol) (PEG), to the solution34. Indeed, when we replaced polyamines with PEG 8000 (9% w/v), we still observed efficient chromosome condensation (Fig. 1e), comparable to polyamines, as reported previously26. Donnan’s theory also predicts that lowering the ionic strength—in the absence of polyamines—leads to chromosome expansion, whereas increasing the ionic strength causes further condensation, in agreement with our observations (Extended Data Fig. 2e). Interestingly, the addition of polyamines led to an inversion of this effect as the interaction between polyamines and DNA itself depends on the ionic strength35,36.

Notably, we observed that decondensed chromosomes were more fragile than condensed chromosomes (Fig. 1f). To test this more systematically, chromosomes were kept at a constant force of 250 pN for 30 min in the presence or absence of condensing agents such as PEG or polyamines. With PEG or polyamines, they showed some viscoelastic creep but rarely extended by more than 15% (one out of seven chromosomes for polyamines; two out of seven chromosomes for PEG). By contrast, in the absence of polyamines or PEG, the chromosomes frequently exhibited stepwise elongations (six out of seven chromosomes; P = 0.01 and P = 0.05, respectively). For four out of the seven chromosomes analysed, chromosome integrity was even compromised such that the chromosome was not able to support forces of 250 pN (marked with red dots in Fig. 1f), which was never observed in the presence of polyamines or PEG (P = 0.03 and P = 0.03, respectively). This shows that compacting agents such as polyamines are crucial for chromosomal integrity.

Thus far, we have used reversible swelling and condensation of the chromosome by modulating the electrostatic and osmotic balance between the chromosome and the surrounding medium. In a second manipulation, we apply high salt concentrations (above 1 M) to irreversibly expand the chromosome. Under these conditions, electrostatic interactions between histone complexes and DNA are weakened, causing the histones to detach, an approach that has already been used by Paulson and Laemmli2. Indeed, when exposed to a buffer containing 1 M monovalent salt (80 mM KCl and 920 mM NaCl), we observed an immediate swelling of the chromosome (Extended Data Fig. 3a,b), which was mostly irreversible when returning to the regular buffer (Extended Data Fig. 3c). This length increase was substantially larger than during reversible ion-mediated chromosome condensation (Fig. 1e). When we monitored the presence of histones on the chromosomes by measuring the H2B-eGFP fluorescence intensity, we observed that the chromosomes were almost completely depleted of histones after roughly 10 min (Extended Data Fig. 3d), whereas histones were stable under regular buffer conditions, independent of the applied force (Extended Data Fig. 3e). Surprisingly, the chromosomes remained structurally intact following this procedure and were able to withstand forces of up to 350 pN, which concurs with reports that the protein scaffold is not perturbed by this treatment37 and that mitotic chromosomes can even assemble in the absence of histones38.

Origin of elasticity in mitotic chromosomes

The two manipulations introduced here provide complementary insights into the mechanics of mitotic chromosomes. For both manipulations, the persistence length Lp of the chromatin fibre—the length scale beyond which thermal fluctuations bend the polymer (Fig. 1b)—is expected to change, as the flexibility of a polyelectrolyte depends on its charge and the solvent39,40. By contrast, the contour length Lc of the chromatin fibre is expected to be unaffected during ion-mediated condensation. However, when histones are depleted under high-salt conditions, the chromatin fibre’s contour length increases dramatically as it is no longer compacted by histones (Fig. 1b)2. Thus, by comparing the mechanics before and after these manipulations, we can gain complementary insights into the underlying basis of chromosomal mechanics.

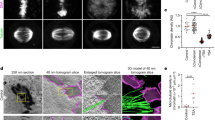
First, we considered how the elasticity of chromosomes changed during ion-mediated chromosome condensation/decondensation. To this end, we measured force–displacement curves on the same chromosome in the absence and presence of polyamines or PEG. These curves showed the characteristic nonlinear mechanical response reported previously22, which is independent of the condensation state (Fig. 2a). At low forces, the force response was approximately linear with a constant stiffness K0, before stiffening set in at the critical force Fc and the stiffness increased dramatically. Both the linear stiffness K0 and the critical force Fc appeared to increase slightly after chromosome condensation by polyamine or PEG (Fig. 2b and Extended Data Fig. 4).

Fig. 2: Characterization of nonlinear chromosomal elasticity.
figure 2

a, Stretch curves of chromosome in the presence (+) and absence (−) of polyamines, where the linear stiffness K0 and the critical force Fc of the decondensed chromosome are indicated. b, Box plots of the linear stiffness (top) and the critical force (bottom) in the absence or presence of polyamines or PEG (linear stiffness: P = 0.19 for polyamines (two-sided t-test for related samples, N = 25 chromosomes), P = 0.03 for PEG (N = 12 chromosomes); critical force: P = 0.03 for polyamines, P = 0.09 for PEG). The box plot marks the quartiles of the distribution, the whiskers show the whole distribution and the centre line marks the median. The differences between the results for − Polyamines and − PEG are presumably due to the use of chromosomes from different preparations. c, The relative change in linear stiffness \({K}_{0}^{{\rm{cond}}}/{K}_{0}^{{\rm{dec}}}\) as a function of the relative change in critical force \({F}_{{\rm{c}}}^{\,{\rm{cond}}}/{F}_{{\rm{c}}}^{\,{\rm{dec}}}\) shows a linear relationship that agrees well with the predictions for a flexible polymer K0 ∝ Fc, whereas it clearly deviates from the prediction for a semiflexible polymer \({K}_{0}\propto {F}_{{\rm{c}}}^{2}\). The error bars show the s.e.m., N = 12 chromosomes for PEG and N = 25 chromosomes for polyamines. d, Stretch curves of a chromosome before histone depletion and after various times of treatment with 1 M salt, measured in regular buffer containing polyamines. We see a drastic elongation, but the general curve shape and the mechanical stability are maintained. e, The relative change in linear stiffness \({K}_{0}^{{\rm{cond}}}/{K}_{0}^{{\rm{dec}}}\) as a function of \(({F}_{{\rm{c}}}^{{\rm{cond}}}/{F}_{{\rm{c}}}^{{\rm{dec}}})/ (\ell {(120\,{\rm{pN}})}^{{\rm{cond}}}/\ell {(120\,{\rm{pN}})}^{{\rm{dec}}})\) shows a linear scaling. Filled symbols compare chromosomes before and after histone depletion, and open symbols compare chromosomes before histone depletion with chromosomes during histone depletion (while in a 1 M salt buffer) (N = 10 chromosomes). f, Schematic illustrating how the mechanical properties of a mitotic chromosome composed of a flexible chromatin fibre depend on the physico-chemical environment. The chromosomes in a–c have been isolated from U2OS cells, the chromosome in d is from HCT116 cells and the chromosomes in e are from both.

Full size image

However, when we analysed how these parameters changed for each individual chromosome by considering the ratio of the linear stiffness in the condensed and decondensed states \({K}_{0}^{{\rm{cond}}}/{K}_{0}^{{\rm{dec}}}\) as a function of the ratio of the critical force in the condensed and decondensed states \({F}_{{\rm{c}}}^{\,{\rm{cond}}}/{F}_{{\rm{c}}}^{\,{\rm{dec}}}\), we observed an approximately linear relationship that is independent of the condensing agent (Fig. 2c). Fitting a power law \({K}_{0} \propto {F}_{{\rm{c}}}^{\alpha }\) to these data disclosed a power-law exponent of α = 1.1 ± 0.24. This observation has important implications because this scaling depends on the physical characteristics of the underlying polymer. Therefore, we model the chromosome as a single effective worm-like chain (WLC) described by Lp and Lc and consider the relation between linear stiffness K0 and critical force Fc (see Methods). When Lc is constant, as expected for ion-mediated condensation, we expect a linear scaling K0 ∝ Fc for a flexible polymer (Lp ≪ Lc)41, whereas for a semiflexible polymer (Lp ≲ Lc), we expect \({K}_{0}\propto {F}_{{\rm{c}}}^{2}\) (refs. 42,43). These relations are independent of the persistence length of the polymer, which depends on the solvent and ionic conditions. Comparing these two models, the scaling behaviour of chromosome data agrees better with the flexible limit of the WLC model (Fig. 2c).

Next, we consider the changes in nonlinear elasticity upon histone depletion. Again, we found that the general shape of the force–extension curve did not change compared with that of untreated chromosomes, apart from an increase in length and a strong decrease in linear stiffness (Fig. 2d and Extended Data Figs. 3c and 5). This directly showed that, although histones are crucial for chromosome compaction, they do not qualitatively define the chromosomal mechanics. During histone depletion, the contour length Lc of the chromatin is expected to change dramatically, causing these data not to follow the simple linear scaling between K0 and Fc (Extended Data Fig. 6a). Thus, the dependency on Lc must be considered (K0 ∝ Fc /Lc; see Methods). Whereas there is no straightforward way to extract the effective contour length of a chromosome from our data, we can assume that the change in the force-dependent chromosome length ℓ(F) (that is, the end-to-end distance) upon histone depletion is dominated by the corresponding change in Lc, such that \(\ell {(F)}^{{\rm{cond}}}/\ell {(F)}^{{\rm{dec}}}\approx {L}_{{\rm{c}}}^{{\rm{cond}}}/{L}_{{\rm{c}}}^{{\rm{dec}}}\) as long as we are sufficiently above the critical force (Fig. 2b). Indeed, when plotting \({K}_{0}^{{\rm{cond}}}/{K}_{0}^{{\rm{dec}}}\) against \(({F}_{{\rm{c}}}^{{\rm{cond}}}/{F}_{{\rm{c}}}^{{\rm{dec}}})/ (\ell {(120\,{\rm{pN}})}^{{\rm{cond}}}/\ell {(120\,{\rm{pN}})}^{{\rm{dec}}})\), we find a relation that is close to linear (Fig. 2e, using the length at 120 pN). This not only endorses that chromosome mechanics are characterized by flexible polymer behaviour but also identifies this polymer as the chromatin fibre.

How do these observations fit our current theoretical understanding of chromosomal mechanics22, that is, the hierarchical worm-like chain (HWLC) model? The HWLC model proposes that mitotic chromosomes are mechanically heterogeneous and behave as a series of nonlinear segments, each of which is characterized by a different linear stiffness k0 and critical force fc (lowercase letters indicate that these parameters relate to chromosome segment and not the whole chromosome). As a result, when a chromosome is stretched, these components stiffen sequentially, giving rise to anomalous stiffening behaviour22, which we observed to be independent of chromosome condensation (Extended Data Fig. 4c). This raises the question of whether an assembly of heterogeneous elements will follow the scaling relations derived above for a single WLC. Indeed, we found that when all individual components of an HWLC follow a scaling law \({k}_{0}\propto {f}_{{\rm{c}}}^{\alpha }\), the stiffness of the entire assembly indeed approaches the same scaling of \({{K}_{0} \propto {F}_{{\rm{c}}}^{\alpha }}\) (see Methods). Furthermore, for sequential stiffening to occur, the HWLC model requires an exponent α < 3/2, which excludes semiflexible WLCs but is satisfied by chromatin behaving like an assembly of flexible WLCs (α = 1), as we argued above.

Taken together, we have demonstrated that chromosomal elasticity originates from the chromatin fibre behaving as a flexible polymer. In this picture, condensation of the chromosome by ions can be understood as a change in the persistence length Lp of chromatin (Fig. 2f), which enables control over the mechanical properties of mitotic chromosomes by modulating their physico-chemical environment, either via more efficient ions such as polyamines or osmolytes such as PEG.

Origin of energy dissipation in mitotic chromosomes

Next, we assessed the role of dissipative, viscous contributions in chromosomal mechanics. Therefore, we oscillated the force applied on the chromosome, similar to active microrheology44. A pre-tension of 50 pN was applied to the chromosome before one of the two traps was oscillated with an amplitude of approximately 100 nm at a frequency ν of 0.1 Hz (Fig. 3a) (see Methods). This enabled us to quantify not only the elastic stiffness K′(ν) from the ratio of the force and distance amplitudes but also the dissipative, viscous stiffness K″(ν) from the phase shift ϕ between force and extension.

Fig. 3: Characterization of chromosomal viscoelasticity.
figure 3

a, Typical force (top) and distance (bottom) traces of an oscillatory measurement, where the data are shown in blue and the sine fit is shown in red. b, Box plot of the loss tangent in the absence and presence of polyamines (PA; P = 0.003, two-sided t-test for related samples, N = 6 chromosomes) or PEG (P = 0.0004, N = 10 chromosomes). The box plot marks the quartiles of the distribution, the whiskers show the whole distribution and the centre line marks the median. c, Box plot of the loss tangent before and after histone depletion in the presence of polyamines (P = 0.0003, two-sided t-test for related samples, N = 8 chromosomes) or PEG (P = 0.05, N = 4 chromosomes) and absence of either (P = 0.94, N = 3 chromosomes). The box plot follows the same definition as in b. d, Loss tangent as a function of the length normalized either to the length of the decondensed chromosome or to the length of the chromosome before histone depletion. N = 12 for PEG, N = 25 for polyamines, N = 8 for histone depletion with polyamines, N = 4 for histone depletion with PEG. e, Proposed model for energy dissipation. We model the chromosome as an elastic scaffold (blue line) in parallel with an effective solution of entangled chromatin loops (grey lines) formed by condensins (red rings). The solution dominates the dissipative response of the chromosome. f, The average normalized viscous and elastic stiffness as a function of the normalized length, both normalized to the values measured for each respective decondensed chromosome. The dashed lines illustrate scalings of ℓ(50 pN)−2 and ℓ(50 pN)−5. N = 12 chromosomes for PEG and N = 25 chromosomes for polyamines. Chromosomes for these experiments were isolated from U2OS and HCT116 cells. In d and f, the error bars show the s.e.m.

Full size image

The elastic stiffness K′ of the chromosomes increased strongly when they were condensed with polyamines or PEG (Extended Data Fig. 6b), as also seen for the linear stiffness (Fig. 2b). Returning the chromosome to polyamine- or PEG-free buffer showed that this was mostly reversible on short timescales, in accord with our observations on the reversibility of ion-mediated condensation (Extended Data Fig. 2a–c). Surprisingly, condensation-induced stiffening was accompanied by an increase in fluidity, that is, the loss tangent tan(ϕ) = K″(ν)/K′(ν) increased (expressing the relative importance of viscous and elastic contributions; Fig. 3b). Although energy dissipation was almost negligible in the decondensed state with a loss tangent of only 0.04, during condensation it increased to 0.15 for polyamines and 0.14 for PEG, leading to appreciable energy dissipation under mechanical load. This dependency of mechanical properties on relatively small changes in ion concentrations means that mitotic chromosomes can be classified as a stimulus-responsive biomaterial45.

Repeating these experiments on chromosomes before and after histone depletion showed that the fluidity increased strongly after histone depletion in the presence of polyamines and slightly in the presence of PEG (Fig. 3c). The increase in fluidity as chromosomes expand upon histone depletion (Fig. 3c) appears to be in contrast to the increase in fluidity as chromosomes condense with polyamines/PEG (Fig. 3b), as both manipulations lead to opposite dependencies of the fluidity on the chromosome size (Fig. 3d).

The key mechanical difference between the two manipulations is that in the case of histone depletion the contour length of the chromatin fibre increases. Our results thus indicate that energy dissipation is affected by the length of the chromatin fibre, and consequently that the chromatin fibre and its organization are at the origin of the observed energy dissipation. Furthermore, the observation that the increase in fluidity was identical for polyamines and PEG (Fig. 3b,d) shows that energy dissipation is not controlled by the charge of the chromatin fibre alone. It also shows that energy dissipation cannot only be explained by polyamine-induced attractive interactions between DNA strands, for example, by bridging them28 or by charge inversion27. Another feasible mechanism for energy dissipation could be based on the binding dynamics of histone complexes. However, as energy dissipation increased after the removal of histone complexes from the chromosome, this also seems unlikely.

In the following, we develop a minimal model to demonstrate that the polymer dynamics of entangled chromatin46,47 can explain the increase in fluidity during ion-mediated chromosome condensation (Fig. 3e). We model the chromosome as an elastic central scaffold in parallel with an effective solution of entangled polymers, representing the assembly of loops extruding from this scaffold. If the central scaffold dominates the chromosome’s elastic response, we expect the storage modulus to exhibit flexible chain scaling, such that K′ ∝ K0 ∝ 1/(LpLc). As the radius of gyration Rg and the initial extension ℓ0 of a flexible chain scale as \({\ell }_{0}^{2} \propto {R}_{{\rm{g}}}^{2} \propto {L}_{{\rm{p}}}{L}_{{\rm{c}}}\), we expect \({K}^{{\prime} } \propto {\ell }_{0}^{-2}\), consistent with the dependency of K′ on the chromosome length that we observed at a pre-tension of 50 pN (Fig. 3f).

Similarly, we assume that the scaling behaviour of K″ is dominated by the effective polymer solution of entangled loops. The plateau modulus G0 of such an entangled solution scales with the number density of entanglement segments: G0/(kBT) ∝ ρ/ℓe, where kB is the Boltzmann constant, T is the temperature, ρ is the polymer length per unit volume and ℓe is the entanglement length48. For flexible chains at intermediate densities, the entanglement length is set by the frequency of interchain contacts, such that ℓe ∝ ρ−1, and consequently G0 ∝ ρ2 (ref. 49). To express K in terms of G0, we use that Young’s modulus (which scales with G0) relates the stress (the force over the cross-sectional area A) to the strain (the extension over rest length ℓ0), so that K″ ∝ G0A/ℓ0 ∝ ρ2A/ℓ0. Finally, we use that ρ ∝ Lc,sol/V, where Lc,sol is the total contour length of polymers in the solution and V = Aℓ0 is the volume. Combining these expressions gives \({K}^{\prime\prime} \propto {L}_{{\rm{c}},{\rm{sol}}}^{2}{V}^{-1}{\ell }_{0}^{-2}\). During ion-mediated condensation, Lc,sol remains constant. Furthermore, chromosome condensation has been observed to be isotropic26, such that \(V \propto {\ell }_{0}^{3}\). In this case, we obtain the central prediction \({K}^{\prime\prime} \propto {\ell }_{0}^{-5}\), which agrees with our observations at a pre-tension of 50 pN (Fig. 3f).

This model not only explains the observed changes in mechanics during condensation but also fits our qualitative observations. First, it does not rely on specific interactions between chromatin and condensing molecules, in line with our observation that condensation by polyamines or PEG results in similar mechanical properties. Second, the model predicts that energy dissipation increases with the contour length of chromatin, explaining the differences that we observed between ion-mediated condensation and histone depletion: a strong increase in the contour length Lc,sol can lead to an increase in fluidity, even as the chromosome expands during histone depletion (such that ℓ0 and V increase). Finally, for mitotic chromosomes K″ has been observed to be only weakly frequency-dependent over a broad range of frequencies22, as often seen in polymer solutions50,51.

Taken together, this leads to the following conceptual picture of mechanical energy dissipation in mitotic chromosomes: during stretching of the chromosome, the chromatin loops need to rearrange. In the swollen state (in the absence of polyamines or PEG), loops can rearrange readily with little energy dissipation. When the chromosome is condensed, however, the loops collapse and entanglement increases leading to energy dissipation. A similar dependency of energy dissipation on external conditions has been observed in the friction between polymer brushes, which strongly decreases with the amount of solvent absorbed by the polymers52,53 and increases with bristle length54.

Conclusion

By combining well-controlled experiments with theoretical polymer models, we were able to gain insight into the underlying physical mechanisms for the elasticity and viscosity of mitotic chromosomes. We have shown that their material properties—including stiffness, density, stability and fluidity—are strongly dependent on the physico-chemical properties of their environment, which classifies mitotic chromosomes as a stimulus-responsive biomaterial.

This effect, owing to the polyelectrolyte characteristics of the chromatin fibre and the loop structure of the chromosome, provides cells with a mechanism for controlling the chromosome material properties during the cell cycle by adding or depleting polyamines and other ions. Recent live-cell imaging experiments have revealed that the stability and proper function of mitotic chromosomes are strongly dependent on histone deacetylation, which, like polyamines, controls chromosome condensation9. Our results suggest that the physico-chemical environment of mitotic chromosomes, in particular the presence of polyvalent ions such as polyamines, may be equally important for the function, mechanics and stability of mitotic chromosomes.

Methods

Buffer compositions

All buffers were made with ultrapure water (MilliQ, Millipore) and filtered (0.2 μm pore size, Whatman) before use.

All buffers contained Tris (15 mM), EDTA (2 mM), KCl (80 mM), NaCl (20 mM), EGTA (0.5 mM) and Tween 20 (0.2%) and were buffered at pH = 8. Polyamine-containing buffer also contained 0.5 mM spermidine and 0.2 mM spermine. Buffer for histone depletion had an increased NaCl concentration (920 mM) to a total concentration of monovalent ions of 1 M. Buffers with doubled salt concentrations contained KCl (160 mM) and NaCl (40 mM), whereas buffers with a decreased salt concentration contained no KCl or NaCl. PEG-containing buffer was supplemented with 9% w/v PEG 8000.

Cell culture and chromosome isolation

All cell lines were cultured in high-glucose GlutaMAX DMEM (Gibco) supplemented with 10% fetal bovine serum (Gibco) and penicillin–streptomycin (Gibco) in a humidified incubator at 37 °C with 5% CO2. For most experiments, chromosomes were isolated from U2OS TRF1-BirA cells with or without H2B-eGFP as described previously22.

In brief, before isolation, the cell growth medium was supplemented for 48 h with 12.2 mg l−1 biotin (Sigma-Aldrich). Cells were stalled in mitosis for 4 h by the addition of 50 ng ml−1 nocodazole (Sigma-Aldrich). Cells were collected via mitotic shake-off, washed multiple times and then subjected to osmotic swelling in 75 mM KCl and 5 mM Tris-HCl (pH 8.0) for 10 min. Cells were washed and resuspended in polyamine buffer (for composition, see above), supplemented with cOmplete Mini protease and PhosSTOP phosphatase inhibitor cocktails (Roche). Cells were then lysed using a Dounce homogenizer via 25 strokes with a loosely fitting pestle. After an additional washing step, chromosomes were purified on a glycerol density gradient (60% glycerol (2 ml) and 30% glycerol (2 ml), each in polyamine buffer) at 1,750g for 30 min. The 60% glycerol fraction contained the purified chromosomes and was stored at −20 °C until use.

For some experiments (see below), chromosomes were isolated from HCT116 TOP2A-mAID H2B-eGFP CDK1as cells infected with lentiviruses introducing TRF1-BirA into the genome (without auxin addition) as described previously22.

The experiments for Figs. 1f and 2a–c were performed with chromosomes isolated from U2OS cells; the experiments for Fig. 2d were performed with chromosomes isolated from HCT116 cells; the experiments for Figs. 1e, 2e and 3 were carried out with both. We did not observe any differences between their mechanical behaviour.

Optical tweezers experiments

The general workflow for studying mitotic chromosomes using optical tweezers has been described previously22. Optical tweezers experiments were performed using a commercial optical tweezers set-up (C-trap, LUMICKS) or a similarly equipped academic set-up described previously55. In both cases, a 20 W trapping laser (1,064 nm; YLR-20-LP, IPG Photonics), a ×60 water immersion objective (Plan Apo VC NA 1.2, Nikon) and multicolour widefield fluorescence imaging were used. A 488 nm excitation laser was used to image both eGFP and intercalator dyes. Furthermore, both traps were equipped with a microfluidic set-up (u-Flux, LUMICKS). The commercial trap was controlled using Bluelake software, whereas the academic set-up was controlled using TWOM software (both LUMICKS). The distance between the trapped beads was determined via camera tracking. Forces were determined using a position-sensitive detector and they were binned to match the frame rate used for distance detection (~20 Hz). All experiments were performed using streptavidin-coated polystyrene beads (4.47 or 4.88 μm diameter, Spherotech). Oscillations of the trap on the academic set-up were generated as described previously22, whereas oscillations of the commercial set-up were enabled using a Bluelake script (LUMICKS).

Trap stiffnesses were calibrated using the thermal noise method before each experiment and were usually around 0.5 pN nm−1. Stretch curves were recorded with a pulling velocity of 0.2 μm s−1 to a maximum force of between 250 and 350 pN. Oscillations were mostly performed at 0.1 Hz around a 50 pN pre-tension. Five cycles of six oscillations each were performed per condition for ion-mediated chromosome condensation; for histone depletion, for each condition one cycle of five oscillations at 0.1 Hz or 20 oscillations at 1 Hz was performed. These parameters were chosen to ensure a good signal-to-noise ratio. We observed that the loss tangent was independent of the frequency and pre-tension in the range used in these experiments. Experiments were carried out at around 27 °C, slightly above room temperature. For the stability assay, a stretch curve was recorded first, before the chromosomes were clamped at 250 pN for 30 min or until the chromosome could not maintain the applied force.

Experiments were performed using five or six channel flow cells. Channel 1 was filled with a given buffer containing polystyrene beads (bead stock suspension (5 μl) in buffer (500 μl)), channels 2 and 3 were filled with the same buffer and channel 4 was filled with the same buffer containing chromosomes (chromosome stock suspension (20 μl) in buffer (400 μl)). Channels 5 and 6 were then filled with different buffers. Before an experiment was performed under new buffer conditions, the flow cell was flushed for 5 s. Stretch experiments were performed both by moving chromosomes from polyamines-/PEG-free buffer to buffer containing either polyamines or PEG and vice versa. For oscillatory experiments, chromosomes were moved from polyamines-/PEG-free buffer to buffer containing either polyamines or PEG and back.

Histone depletion

For in situ histone depletion, channel 5 of the flow cell was filled with buffer containing a total concentration of monovalent salt of 1 M. Individual chromosomes were first clamped between two beads and then moved to channel 5 for a defined time. Changes in the mechanical properties were assessed via either force–distance curves or oscillatory measurements. In both cases, one measurement was performed before histone depletion, one measurement was taken during the treatment in channel 5 (towards the end of the specified incubation time) and one measurement was carried out after the treatment. For the scaling analysis, we compared not only the curves before and after treatment but also the curves before and during treatment, where we see not only the effect of histone depletion but also the difference between the regular buffer and the 1 M salt buffer.

Data analysis

Oscillatory experiments

Oscillatory experiments were analysed using Matlab and Python scripts56,57,58. First, the parts of the recorded signal containing oscillations were identified by calculating the cross-correlation between the measured distance and the expected oscillation (on the basis of the known number of oscillations and frequency). Therefore, the distance signal was preprocessed using a low-pass filter at half the expected oscillation frequency and by detrending the data (although further analysis continued with the raw signal). Next, the parts of the signal containing oscillations were fitted with a sine function. As the force and distance signals are differently measured and processed, it cannot be assumed that the recorded timing is precise. Therefore, in addition to force and distance we also analysed the bead positions as recorded on the camera, which is in phase with the force acting on the bead and intrinsically synchronized with the distance measure. These three signals (distance, force and position of one bead) were fitted with a sinusoidal function \({a}_{1}\cos (2\uppi {\nu}_{1}t)+{a}_{2}\sin (2\uppi {\nu}_{2}t)+mt+c\) with amplitudes a1 and a2, frequencies ν1 and ν2, a linear drift term m and a constant offset c. The sum of cosine and sine yielded more robust fit results and can be transferred to a sine function with a phase shift \(A\sin \left(2\uppi \nu t-\phi \right)\), with the amplitude \(A={\rm{sgn}}({a}_{1})\sqrt{\left({a}_{1}^{2}+{a}_{2}^{2}\right)}\), frequency ν and phase \(\phi =\arctan \left({a}_{2}/{a}_{1}\right)\); \({\rm{sgn}}({a}_{1})\) denotes the sign of the fitted amplitude. The frequency was set at the experimental value and not used as a fit parameter. The complex stiffness K* was then calculated using the amplitude values of the force and distance oscillations AF and Ad, respectively, and the phase of the respective bead and distance oscillations ϕx and ϕd as \({K}^{* }={A}_{F}/{A}_{d}{\mathrm{e}}^{i({\phi }_{d}-{\phi }_{x})}\).

Stretch curves

Length changes during changes in the buffer condition were read at 50 pN.

Analysis of force–distance curves was performed using Python scripts using jupyter, the numpy/scipy framework56,57, and matplotlib and seaborn for visualization58. To calculate the stiffness, force and distance signals were smoothed using a Savitzky–Golay filter from the scipy signal toolbox, with a window length of 81 data points and a third-degree polynomial. Then, the stiffness K was calculated by numerical differentiation of force F with respect to distance d. To obtain the critical force, a piecewise linear function was fitted to the stiffness as a function of force on a log–log scale. Therefore, the stiffness was interpolated to a logarithmic force scale, to obtain evenly spaced data points after taking the logarithm. Then, the natural logarithms of force ln(F) and stiffness ln(K) were calculated and fitted with a piecewise function y = ln(K0) for x ≤ ln(Fc) and \(y=m x-m \ln ({F}_{{\rm{c}}})+\ln ({K}_{0})\) for x > ln(Fc) to determine the initial stiffness K0, the critical force Fc and the stiffening exponent m. Whereas this method enables the robust determination of the critical force, the initial stiffness provided by this method turned out to be prone to artefacts. Therefore, the linear stiffness was determined by fitting a straight line to the initial part of the force–distance curve up to 90% of the critical force. Only datasets where critical force and linear stiffness could be determined unequivocally for the condensed as well as the decondensed chromosome were used for further analysis. This condition was met by 25 out of 42 chromosomes for polyamine-mediated condensation and 13 out of 22 chromosomes for PEG-mediated condensation.

To quantify the scaling behaviour of changes in stiffness and critical force, the power-law function axb was fitted to the data using orthogonal distance regression (scipy.odr) to the individual data points \({F}_{{\rm{c}}}^{\,{\rm{cond}}}/{F}_{{\rm{c}}}^{\,{\rm{dec}}}\) and \({K}_{0}^{{\rm{cond}}}/{K}_{0}^{{\rm{dec}}}\). The uncertainties of these data points were calculated by error progression from the uncertainty of the fits used to determine Fc and K0, with a lower bound of 0.25 pN for the absolute error in Fc and 1% for the relative error in K0.

For statistical difference testing, the t-test for related samples, the t-test for independent samples and the Fisher exact test were used (function ttest_rel, ttest_ind and fisher_exact in scipy.stats).

Image analysis

Fluorescence images were visualized using imagej59. Analysis of the fluorescence intensity of labelled histones was performed in python. Images were loaded using Pylake (LUMICKS)60, then the background intensity was determined for each image as the most likely intensity of the whole image using a kernel density estimate. The total intensity of the background-corrected image was then summed up to give the total intensity of fluorescence of the labelled histones.

Data presentation

Box plots were created using the seaborn Python package58. The box indicates the quartiles, whiskers indicate the range of the whole distribution without outliers and the centre line marks the median. The error bars show the s.e.m.

Stiffness scaling relations

Flexible polymer

For the scaling analysis (Fig. 2c,e), we model the chromosome as a single WLC with an effective persistence length Lp and an effective contour length Lc, corresponding to the stretched-out length of the chromosome without the removal of cross-links. If the effective polymer is flexible (Lp ≪ Lc), the critical force Fc and the linear stiffness K0 are given by41

$${F}_{{\rm{c}}}=\frac{{k}_{{\rm{B}}}T}{{L}_{{\rm{p}}}}$$
(1)

and

$${K}_{0}=\frac{3{k}_{{\rm{B}}}T}{2{L}_{{\rm{p}}}{L}_{{\rm{c}}}}.$$
(2)

We can combine these two equations to eliminate the dependency on the persistence length Lp to obtain

$${K}_{0}=\frac{3{F}_{{\rm{c}}}}{2{L}_{{\rm{c}}}}.$$
(3)

When we consider the relative changes in these parameters between the condensed and the decondensed states (noted by superscript cond and dec, respectively) we find

$$\frac{{K}_{0}^{{\rm{cond}}}}{{K}_{0}^{{\rm{dec}}}}=\frac{{F}_{{\rm{c}}}^{\,{\rm{cond}}}{L}_{{\rm{c}}}^{{\rm{dec}}}}{{F}_{{\rm{c}}}^{\,{\rm{dec}}}{L}_{{\rm{c}}}^{{\rm{cond}}}}.$$
(4)

As the stretched-out length of a chromosome will be determined by the amount of chromatin between the cross-links in the chromosome, Lc will scale with the contour length of the chromatin fibre. Hence, as the contour length of chromatin is constant during condensation, this gives us a prediction for the relative changes in critical force Fc and linear stiffness K0 during chromosome condensation:

$$\frac{{K}_{0}^{{\rm{cond}}}}{{K}_{0}^{{\rm{dec}}}}=\frac{{F}_{{\rm{c}}}^{\,{\rm{cond}}}}{{F}_{{\rm{c}}}^{\,{\rm{dec}}}}.$$
(5)

Semiflexible polymer

If the effective contour length of the chromosome is of the order of its persistence length, the critical force Fc and the linear stiffness K0 are given by42,43

$${F}_{{\rm{c}}}=\frac{{k}_{{\rm{B}}}T{L}_{{\rm{p}}}}{{L}_{{\rm{c}}}^{2}} \propto \frac{{L}_{{\rm{p}}}}{{L}_{{\rm{c}}}^{2}}$$
(6)

and

$${K}_{0}=\frac{90{k}_{{\rm{B}}}T{L}_{{\rm{p}}}^{2}}{{L}_{{\rm{c}}}^{4}} \propto \frac{{L}_{{\rm{p}}}^{2}}{{L}_{{\rm{c}}}^{4}}.$$
(7)

We can combine these two equations to eliminate the dependency on the persistence length Lp and the effective contour length Lc to find that

$${K}_{0} \propto {F}_{{\rm{c}}}^{2},$$
(8)

which directly gives us a predicted scaling between changes in the critical force and linear stiffness during chromosome condensation or histone removal:

$$\frac{{K}_{0}^{{\rm{cond}}}}{{K}_{0}^{{\rm{dec}}}}={\left(\frac{{F}_{{\rm{c}}}^{\,{\rm{cond}}}}{{F}_{{\rm{c}}}^{\,{\rm{dec}}}}\right)}^{2}.$$
(9)

Hierarchical worm-like chain

We now consider a serial assembly of N polymer elements, which we call an HWLC, with the critical force fc of each element sampled from a power-law distribution with probability density function \(P({f}_{{\rm{c}}})\propto {f}_{{\rm{c}}}^{\,-\beta }\) and the linear stiffness scaling as \({k}_{0}\propto {f}_{{\rm{c}}}^{\alpha }\) (ref. 22). Here, Fc and K0 are the critical force and linear stiffness of the whole assembly, that is, the chromosome, whereas fc and k0 are the critical force and linear stiffness of an individual element. The critical force of the assembly will be given by the smallest critical force of its elements: Fc = fc,1 for fc,1 < fc,2 < … < fc,N. The assembly’s linear response spring coefficient can be expressed as

$${K}_{0}^{-1}=\mathop{\sum }\limits_{i=1}^{N}{k}_{0,i}^{-1}.$$
(10)

By assuming a scaling relation \({k}_{0}\propto {f}_{{\rm{c}}}^{\alpha }\) for all elements, we find

$$\frac{{F}_{{\rm{c}}}^{\alpha }}{{K}_{0}}=\mathop{\sum }\limits_{i=1}^{N}{\left(\frac{{f}_{{\mathrm{c}},1}}{{f}_{{\mathrm{c}},i}}\right)}^{\alpha }.$$
(11)

We now claim that the right-hand side of the expression approaches a constant for sufficiently high N. To show this, we define a random variable X(fc) that follows a uniform distribution. The expected separation between two subsequent samples, X(fc,i) − X(fc,i+1), can then be approximated by a constant Δ proportional to 1/N. To illustrate, if we sample ten points uniformly from the interval (0, 10) and sort them by magnitude, the distance between two neighbouring samples will be approximately equal to unity.

We first take β → 0, so that fc itself is uniformly distributed. Hence we have fc,i ≈ fc,1 + (i − 1)Δ, where Δ ∝ 1/N. We further note that fc,1 ≈ Δ, and hence

$$\frac{{f}_{{\mathrm{c}},1}}{{f}_{{\mathrm{c}},i}}\approx \frac{1}{i},$$
(12)

and Equation (11) therefore approaches the Riemann zeta function.

We now take β = 1. In this case, the variable log(fc) is uniformly distributed, and hence we expect that \(\log (\;{f}_{{\mathrm{c}},i-1})-\log (\;{f}_{{\mathrm{c}},i})\propto 1/N\), and \(\frac{{f}_{{\mathrm{c}},i-1}}{{f}_{{\mathrm{c}},i}}\approx r\) where r ∝ e1/N is a constant. We then write the ratios in Equation (11) as

$$\frac{{f}_{{\mathrm{c}},1}}{{f}_{{\mathrm{c}},i}}=\frac{{f}_{{\mathrm{c}},1}}{{f}_{{\mathrm{c}},2}}\frac{{f}_{{\mathrm{c}},2}}{{f}_{{\mathrm{c}},3}}\ldots \frac{{f}_{{\mathrm{c}},i-1}}{{f}_{{\mathrm{c}},i}}\approx {r}^{-(i-1)}.$$
(13)

Equation (11) then resembles a geometric series with common ratio rα.

Finally, for β ≠ 1, \(X({f}_{{\rm{c}}})={f}_{{\rm{c}}}^{1-\beta }\) follows a uniform distribution. Rewriting Equation (11) as

$$\frac{{F}_{{\rm{c}}}^{\alpha }}{{K}_{0}}=\mathop{\sum }\limits_{i=1}^{N}{\left(\frac{X(\;{f}_{{\mathrm{c}},1})}{X(\;{f}_{{\mathrm{c}},i})}\right)}^{\alpha /(1-\beta )},$$
(14)

we recover the case for a uniformly distributed fc, with β = 0; the exponent in the sum is simply replaced by α/(1 − β). We note that the Riemann zeta function converges for exponents α/(1 − β) > 1 and 1 > β only. Our previous work suggests 1 − β ≈ α − 0.85, and hence the first condition is satisfied when α > 0.

Having shown that the right-hand side of Equation (11) is approximately constant when \(P({f}_{{\rm{c}}})\propto {f}_{{\rm{c}}}^{\,-\beta }\), α > 1 − β and β ≤ 1, we therefore find that, for sufficiently high N, the stiffness of the HWLC assembly scales as \({K}_{0}\propto {F}_{{\rm{c}}}^{\alpha }\) when the individual components follow the same scaling \({k}_{0}\propto {f}_{{\rm{c}}}^{\alpha }\).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.