Main

Tremendous progress in the ability to organize nanoscale components through bottom-up assembly1,2,3 has been demonstrated in recent decades. This has led to greater insight into the contributions of component shapes, interactions and entropic effects to self-assembly processes4,5,6,7,8,9. Although these studies bring an understanding of the fundamental reasons for the formation of nanoscale structures, there is an increasing need to generate nanomaterials on demand. This quest for self-assembly to provide fabrication-by-design capabilities is being tackled through emerging inverse design approaches, which focus on revealing how characteristics of individual components have to be tuned to form a specifically targeted structure4,5,10,11,12,13,14. Addressing this fabrication challenge is particularly critical due to the limitations of traditional methods for generating designed, three-dimensional (3D) nanoscale materials and devices with control over multiple scales and material types, and this presents a critical manufacturing challenge for diverse new applications. This level of control is needed to couple physical effects at different length scales and achieve desired functionality. For example, hierarchical structures exhibit novel optical properties due to the combination of plasmonic, photonic and light propagation effects15,16,17. Similarly, structures with this type of organization possess enhanced mechanical resilience, fracture toughness and high deformability16,18. Such architectures also show promise for addressing outstanding obstacles in energy storage and conversion, as well as catalysis and purification19.

The power to form complex 3D organizations has long been the domain of biological systems, providing advantages for physical properties such as bond strength, structural colouring and mass transport20,21. Nature achieves such bio-organization predominantly through non-equilibrium material growth driven by reactions, kinetic effects and feedback mechanisms, where genes orchestrate the processes. In man-made materials, nucleic acids have attracted much attention as they can directly encode complex architectures via sequence-specific Watson–Crick bonds. Diverse DNA-based materials have been demonstrated through the coordination of DNA bonds for nano-objects, including DNA bricks22, 2D origami assemblies23,24, pegboards25, nanoparticle (NP) lattices26,27,28,29, quasicrystals30,31 and DNA-based ‘material voxels’23,32,33,34. While the DNA-encoded (‘coloured’ or chromatic) interactions offer vast design possibilities by controlling bond specificity and valence9,12,14,23,35,36, defining local binding rules to assemble desired large-scale organization remains challenging. Despite demonstrations of the ability to build 3D nanomaterials that incorporate NPs or proteins32,37,38,39,40, a comprehensive strategy for designing and realizing hierarchically organized nanocomponents in a spatially prescribed manner is still lacking. Fundamentally, the key questions are how to coordinate local, chromatic bonds to direct organization across multiple scales, and what guiding principles will enable the practical realization of targeted nanoscale architectures.

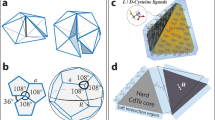
In this Article we introduce and experimentally and computationally validate an inverse design approach for the assembly of desired lattice architectures. This approach translates a prescribed structural ‘blueprint’ into a set of nanoscale components with directional, DNA-encodable bonds. One such set can encode the equilibrium assembly of the target structure; however, it is not inherently unique. Although different sets may achieve the same outcome, the assembly pathway for each might vary, and achieving the equilibrium state may be difficult. We hypothesize that the desired 3D hierarchical architecture can be represented by a set of specific nanocomponents, and that minimizing the information required to encode their chromatic bonds is critical to the successful assembly of the desired structure. This minimization of encoding information (here termed compression) is the underlying principle in our inverse design strategy (Fig. 1). It is achieved by accounting for the intrinsic symmetry of the targeted structure constructed from material voxels, which are DNA frames with sequence-encoded and spatially defined bonds. In our inverse design approach, the arbitrarily defined hierarchical 3D organization is achieved by defining a set of voxels that form a repetitive motif. We term the set of unique voxels required to create this structural motif a ‘mesovoxel’. A hierarchically organized nanostructure with long-range order is formed using this motif. We stress that a mesovoxel is a conceptual motif to guide the design and assembly, and the final larger-scale structure is achieved via a one-pot assembly upon mixing all constituent voxels.

Fig. 1: Inverse design and assembly of hierarchically ordered 3D nanostructures through voxels encoded with chromatic and directional bonds.
figure 1

a, A desired 3D hierarchically ordered crystal of nanocomponents can be constructed from material voxels, consisting of a DNA frame that provides intervoxel chromatic binding and valence-defined coordination of bonds for internally bound components. The set of voxels defines a prescribed repetitive motif, or mesovoxel, which is a hierarchical unit block. A mesovoxel consists of a voxel set that can undergo spatial transformations, associated with symmetries of the target organization of NPs, to hierarchically construct a 3D crystal using three tiers of chromatic bond descriptors: Via, Vmb and Vec. Background voxels are paler with no chromatic bonds shown to improve image clarity, but they possess their own binding colours in practice, as discussed in the text. Experimental implementation of this schematic concept uses a DNA origami octahedron as the voxel and Au NPs functionalized with different ssDNA coronas as the internally bound nanocomponents. In the schematic representation, bond colours (subscripts a, b, c) are represented as either standalone integers or in combination with a ‘C’ to represent a bond colour complement. b, A range of 3D NP crystals are explored in this work, all synthesized by implementing chromatic binding in a simple cubic grid built from DNA octahedra, as shown in the scanning electron microscopy (SEM) images (left). NP organizations are shown on the right, next to a corresponding repetitive motif.

Full size image

We experimentally demonstrate the realization of the proposed strategy to design, encode and assemble 3D hierarchically ordered organizations of NPs (Fig. 1a) for several exemplary cases (Fig. 1b): (1) low-dimensional organizations with coupled length scales in different crystal directions; (2) a nanoscale analogue of a face-centred perovskite crystal; (3) a hierarchically prescribed crystal structure assembled from helical motifs; and (4) an inverse design of plasmonic elements with a photonic response, specifically a NP-based distributed Bragg reflector (DBR). For selected systems, we explored how the degree of information compression within the mesovoxel design affects assembly outcomes. With recently shown capabilities to convert DNA assemblies into inorganic 3D nanostructures with diverse properties41,42, and their suitability for conventional cleanroom processing43, this DNA-based inverse design strategy offers a new methodology for 3D nanofabrication of nanomaterials with complex organizations.

Material design approach

We propose an inverse assembly strategy based on the compression of the information required to define individual voxels to create arbitrarily defined, hierarchically ordered 3D structures with targeted nanocomponent arrangements, as schematically illustrated in Fig. 1a. The core nanoscale building block of a structure, a material voxel, can host nanoscale cargo or remain empty. The hierarchically organized 3D structure is composed of a repetitive motif (mesovoxel) with the desired arrangements of nanocargo dictated by the set of encoded voxels; these mesovoxels can assume any voxelated shape (Fig. 1a). The identity of each voxel is determined by three descriptors of its encoded (chromatic) bonds: Via for internal (i) binding (hosting nanocomponents) and Vmb and Vec defining a voxel’s external bonds, with a, b, c representing bond colours. Vmb encodes local chromatic valence, which allows the formation of a mesovoxel (m) through coordinated bond sets of all voxels in the mesovoxel. Vec governs how mesovoxels assemble (external mesovoxel bonds, e) into a hierarchically ordered architecture. By leveraging symmetry operations (for example, translations, reflections, rotations, screw axes and so on), our inverse design approach finds equivalent voxels in the structure, which minimizes the number of distinct voxels and bond types required to define a mesovoxel. It is important to note that the same target structure may be achieved through different mesovoxel designs with different degrees of information compression that may undergo different assembly pathways. The mesovoxel descriptor across this work accounts for different attributes, including the number of voxels, the number of unique intervoxel chromatic bonds and the number of internal (intravoxel, for carrying cargo) chromatic bonds. This is captured in the mesovoxel descriptor [Nv, Ne, Ni], where Nv, Ne and Ni represent the number of voxels, the number of external colours (unique Vmb + Vec) and the number of internal colours (unique Via), respectively. Importantly, while this descriptor denotes a composition of voxels and bonds in a mesovoxel, it does not provide the specific architecture of bonds arrangements within a given mesovoxel design. All mesovoxel designs explored in this work are summarized in Supplementary Table 5.

We used a DNA origami octahedron (with 12 edges of six-helix bundles) as the material voxel, which naturally forms a cubic grid, although other voxel geometries32,33,34 can produce grids of different symmetries. Each voxel includes eight identical single-stranded DNA (ssDNA) ‘sticky ends’ for binding internal cargo and four identical sticky ends at each vertex for ‘chromatic’ intervoxel bonds, which pair only with complementary ssDNA on other voxels (avoiding designs with pairing on the same voxel). For clarity, we use a ball-and-stick schematic: spherical particle colours show internal binding ‘colours,’ while dotted-stick colours represent external binding ‘colours,’ with complements indicated by inverse colour patterns. We used gold (Au) NPs grafted with complementary binding strands as nanocargo, but different inorganic and biomolecular cargo can be encapsulated, as has been demonstrated in previous works32,38.

The assembly pathways for such multi-component systems may be dependent on a specific set of voxels; thus, it is not immediately clear which mesovoxel is best suited to form a target structure. Nor is it obvious whether there is an optimal number of voxel types and bond colours that maximizes the fidelity of a targeted structure, given the enthalpic and entropic influences on voxel bindings and orientations as well as competing pathways. Cooperative binding, often found in self-assembling systems, can be reduced to avoid detrimental growth complexities33,44 or exploited for controlled growth via seeding45, yet its effect on 3D crystal formation is still not well understood. We show that our inverse design approach allows the assembly of the same ordered superlattices through various mesovoxels (Supplementary Table 5), ranging from ‘minimal’ sets with the most compressed information to more ‘over-prescribed’ designs with additional addressability. Modelling and experiments reveal that minimal sets generally yield better assembly outcomes, as is evident from the degree of crystallinity, highlighting information minimization as an important principle for realizing complex multi-component architectures.

In this work we focused on the assembly of structures using encoded bonds with similar interaction energies; intervoxel DNA binding sequences were therefore designed to have similar melting temperatures (design rules are presented in Supplementary Section I(b)). The differentiation of bonds by energy could be used as an additional means to control the assembly pathway and crystal growth40, but this aspect is not within the scope of this work. Crystal formation in this study occurs following a one-pot mixing of a set of voxels and NPs, followed by a thermal annealing protocol (Supplementary Section I(e)) that cools slowly from 50 °C to room temperature to account for energy differences. The full sets of DNA sequences (colours) used throughout this work are included in Supplementary Tables 6–10.

Low-dimensional NP organizations within a 3D grid

We first illustrate how to design and form low-dimensional NP motifs that break isotropic spacing within a 3D grid, creating string (1D) and plane (2D) arrangements (Fig. 2a,c). Both designs use the smallest possible centre-to-centre spacing between particles in a simple cubic grid defined by our octahedral frames. By exploiting symmetries in the target motifs, the total numbers of voxel types and chromatic bonds are minimized from a fully prescribed [8,24,1] design, where each voxel in the mesovoxel is unique. For instance, the 3D array of alternating NP-filled and empty 1D strings requires only four voxel types, three external binding colours and one internal binding colour for the single NP type. These external colours arise from the need for two different Z-axis chromatic bonds among the empty and NP-filled 1D strings, alongside an additional chromatic bond to connect the strings in the X–Y plane. The resulting [4,3,1] mesovoxel assembles into the desired architecture, as confirmed by small-angle X-ray scattering (SAXS) measurements (Fig. 2b and Supplementary Fig. 28). A primitive tetragonal lattice forms with centre-to-centre NP spacings of 59.1 nm and 83.6 nm for in-string and interstring NP arrangements, respectively, matching the design.

Fig. 2: 1D and 2D hierarchical NP structuring using different arrangements of the same external chromatic set.
figure 2

a, 3D assembly of 1D particle strings based on Mesovoxel 1, where origami particles bind at a coordination of 180°. b, Experimental (black) and modelled (red) structure factors, or S(q), as a function of the wavevector transfer q, for 1D particle strings. The associated locations of Bragg peaks are also shown (Supplementary Fig. 28). The inset shows the 2D SAXS pattern, with brighter colour representing stronger scattering intensity. The model corresponds to a tetragonal primitive unit cell with lattice parameters a = b = 83.6 nm, c = 59.1 nm and α = β = γ = 90°. c, 3D assembly of 2D particle planes based on Mesovoxel 2, where particles bind at a coordination of 90° with a valence of four, separated along the Z axis by an empty voxel layer. d, Experimental (black) and modelled (red) S(q) for 2D particle planes. The associated locations of Bragg peaks are also shown (Supplementary Fig. 29). The inset shows the 2D SAXS pattern. The model corresponds to a tetragonal primitive unit cell with lattice parameters a = b = 59.1 nm, c = 118.2 nm and α = β = γ = 90°. e, SEM images (top and middle) of silicated assemblies show domains with sizes of ~10 µm and a TEM image after FIB sectioning (bottom) provides real-space evidence of stacked planar organizations.

Source data

Full size image

Similarly, using different symmetry operations, this approach can be applied to assemble organizations with alternating planes of NPs and empty voxels organized in a 3D grid (Fig. 2c). The fully prescribed design would again be an [8,24,1] mesovoxel, but in a similar manner to the first system can be reduced to a [4, 3, 1] mesovoxel. In this case, the coordination of colours is transformed to be planar, using two different external bonds for the X–Y alternating planes and a single colour on the Z axis. This organization has a signature of a primitive tetragonal crystal phase confirmed by SAXS, with NP spacings of 59.1 nm for particles in the X–Y plane (Fig. 2d and Supplementary Fig. 29) and 118.2 nm for stacked 2D planes on the Z axis. Following structure silication, we performed SEM imaging (Fig. 2e) and transmission electron microscopy (TEM) imaging after focused-ion beam (FIB) sectioning (Fig. 2e, bottom). The imaging reveals that crystals possess long-range order with crystallite dimensions of ~10 µm, and that the particles are arranged in planes, confirming the design (Fig. 2c) and experimental realization (Fig. 2e and Supplementary Fig. 51).

The string and plane NP arrangements discussed here were inversely designed according to desired NP motifs, as opposed to the direct design of a unit cell. However, the mesovoxel methodology can also be applied to explicitly design a desired crystallographic unit cell and more complex NP motifs. Importantly, different mesovoxels can be used depending on differing levels of binding information. In the following sections, we realize the synthesis of more complex structures and elucidate the effects of information compression on the resulting crystals.

Nanoscale face-centred perovskite crystal structure

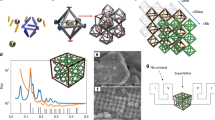
To demonstrate a structure mimicking an atomic crystal, we targeted a nanoscale face-centred perovskite arrangement (Fig. 3a), showcasing different assembly routes and multi-component loading. A fully prescribed unit cell can be defined by an [8,24,3] mesovoxel, but we can reduce these values by taking crystal symmetry into account. At the same time, by considering different mesovoxel designs, we probed the effect of encoding information on assembly. By exploiting the unit cell’s symmetries, we defined two mesovoxels: Mesovoxel 3 (minimal design using one particle type) and Mesovoxel 4 (over-prescribed design using three particle types). For Mesovoxel 3, we identified four unique voxel types—one empty edge voxel and three with distinct NP locations capable of holding different nanocargo (body-centred, face-centred, corner)—yielding again a [4, 3, 1] mesovoxel when using one particle type, but with a different binding layout to Mesovoxels 1 and 2. Optical imaging, SEM and SAXS (Fig. 3a and Supplementary Figs. 30 and 52) confirm particle ordering and the cubic morphology of the superlattice (matching the underlying simple cubic framework) with domain sizes of up to 12 µm.

Fig. 3: Assembly of a prescribed nanoscale analogue of a face-centred perovskite crystal structure using designed sets of mesovoxels with different degrees of information.
figure 3

a, Left: a face-centred perovskite crystal can be designed using different mesovoxels. Middle: Mesovoxels 3 and 4, which encode different assembly information through voxels with different bond symmetries (structures shown on the left), are used to assemble face-centred perovskite crystals. Crystal formation is visualized by optical microscopy (empty crystal, left) and SEM imaging (right). Right: the face-centred perovskite structure of particles is confirmed through SAXS with the experimental S(q) shown for structures formed using Mesovoxel 3 (black) and Mesovoxel 4 (blue), with modelled S(q) (red). The associated diffraction peak locations are also shown. The SAXS data are normalized by the first peak position (q0) to account for the slight shift (<0.5 nm) in the lattice parameter due to sample-to-sample variations in divalent salt concentrations (see also control experiments in Supplementary Fig. 50). Peak positions were normalized by the centre of the first peak. b, TEM image after FIB sectioning, with green circles indicating NP positions. c–g, Experimental (black) and modelled (red) S(q) (Supplementary Figs. 31–38) with inset 2D SAXS patterns for structures with different layouts of occupied particle positions in Mesovoxel 4: corner only (c), faces only (d), centre only (e), corner and faces (f) and corner and centre (g). Corner only and centre only correspond to a simple cubic lattice with lattice parameters a = b = c = 118.2 nm and α = β = γ = 90°. Faces only corresponds to a body-centred tetragonal lattice with a = b = 83.6 nm, c = 118.2 nm and α = β = γ = 90°. Corner and faces corresponds to a face-centred cubic lattice with a = b = c = 118.2 nm and α = β = γ = 90°. Corner and centre corresponds to a body-centred cubic lattice with a = b = c = 118.2 nm and α = β = γ = 90°. The S(q) model for the perovskite design is based on face-centred perovskite unit cell with a = b = c = 118.2 nm and α = β = γ = 90°. h, Modelled crystal growth of a DNA scaffold demonstrates crystallization using equivalents of Mesovoxel 3 (left) and Mesovoxel 4 (middle), and a fully prescribed 27-voxel cell that shows no crystal formation (right). The accompanying plot shows the numbers of discrete clusters in the simulation versus the numbers of Monte Carlo simulation steps. Any free, unbound entity is designated as a single cluster.

Source data

Full size image

Building on the successful perovskite-type NP assembly from Mesovoxel 3, we explored the over-prescribed Mesovoxel 4 that incorporates additional unique voxels and bonds. We identified the design of Mesovoxel 4 by applying a four-fold Z-axis rotational symmetry around the central particle and mirror symmetry in the X–Y plane (Supplementary Fig. 48), yielding a [6,7,3] mesovoxel. Three different internal chromatic encodings allow the incorporation of particles in body-centred (red), face-centred (blue) and corner (green) arrangements (Supplementary Fig. 25). Optical imaging, SEM and SAXS (Fig. 3a and Supplementary Figs. 31–39) confirm the formation of the intended crystal structure. By selectively introducing the three differently encoded NPs, we produced subphases—face-centred cubic, body-centred cubic, body-centred tetragonal and simple cubic lattices—as verified by SAXS and cross-sectional SEM/TEM on silicated samples (Fig. 3b–g and Supplementary Figs. 52 and 53).

Compared with the cubic morphology formed from Mesovoxel 3, crystals formed from Mesovoxel 4 exhibit a ‘pancake’ shape and smaller domain sizes (up to 4 μm), indicating a different assembly pathway. Nevertheless, SAXS data (Fig. 3a) confirm that both mesovoxel designs form the face-centred perovskite unit cell. Mesovoxel 3 shows less broadening in the high-q region, suggesting more ordered domains. Scherrer analysis (Supplementary Section III) reveals micrometre-scale grain sizes in both samples (Supplementary Fig. 9), consistent with the optical and electron microscopy results. Because scattering and imaging probe different lattice characteristics, these results provide only qualitative comparisons, further limited by the <1 μm probing window of SAXS. For reference, a simple cubic lattice formed by a two-voxel/single-colour design32 shows a similar correlation length to Mesovoxel 3 (Supplementary Figs. 49 and 50), indicating that minimal additional design information does not markedly affect domain size.

Further comparing Mesovoxel 4 with Mesovoxel 3 reveals that the minimal Mesovoxel 3 consistently forms larger (~12 μm) and better-defined cubic domains (Fig. 3a(i),(ii)). Both systems reach high structural order, but the higher degree of information compression (fewer bonds and voxels) of Mesovoxel 3 results in a better-assembled structure. Mesovoxel 3 has more competing growth modes, whereas the increased binding specificity of Mesovoxel 4 reduces competition but adds stricter orientation requirements, potentially introducing more defects that are harder to correct during annealing.

To investigate hierarchical assembly computationally, we ran molecular simulations on three simple cubic crystal systems built from voxels each containing a nanoparticle but with differing mesovoxel designs: [3,4,1] and [6,7,1] mesovoxels corresponding to Mesovoxel 3 and 4 (differing only in internal bond designation Ni) and a fully prescribed 3 × 3 × 3 [27,81,1] mesovoxel, in which the number of voxels corresponds to the face-centred perovskite unit cell. This fully-prescribed descriptor differs from the previous [8,24,3] descriptor discussed above because [27,81,1] arises from a strict repetitive unit cell rather than a motif that provides appropriate nanoparticle positions in the face-centred perovskite unit cell. Each voxel was modelled as an octahedron with equivalent binding energies at the vertices, but chromatic bonds were encoded according to the mesovoxel designs. We modelled these three mesovoxels using Monte Carlo simulations of hard polyhedra (Fig. 3c, Supplementary Figs. 14–16 and Supplementary Section IV). We found that the fully prescribed 3 × 3 × 3 mesovoxel remained unassembled or formed only small clusters over the simulation timescale, while Mesovoxels 3 and 4 crystallized. The behaviour of crystallite size as a function of time implies a lower nucleation rate for Mesovoxel 3 versus Mesovoxel 4. While Mesovoxel 3 nucleated more slowly than Mesovoxel 4, it ultimately showed faster cluster growth, resulting in larger crystals (Supplementary Fig. 16). These simulations agree with experimental results (Fig. 3a). Furthermore, the total system energy (Supplementary Fig. 16) for the fully prescribed crystal plateau is lower, indicating that the larger numbers of unique voxels and bonds lead to smaller crystal sizes and reduced crystal quality. We attribute this to fewer correctly oriented bonds and a higher entropic penalty during crystallization. Conversely, fewer voxels and bond types allows more competing growth modes (reduced bond specificity), delaying 3D crystal nucleation yet ultimately producing larger crystals (Fig. 3h). Imaging (Fig. 3a and Supplementary Fig. 52) supports this finding, as the more prescribed binding scheme of Mesovoxel 4 yields smaller crystals and a higher number of crystals than that of Mesovoxel 3.

Designed organization of ordered helical motifs

Plasmonic and light-emitting chiral clusters are attractive because of their light manipulation capabilities46,47,48, yet forming 3D crystals from chiral NP motifs remains challenging due to the complexity of such intricate organizations. We applied our inverse design approach to realize a crystal with a helical NP motif (Fig. 4a); if fully prescribed, it would require a [16,48,1] mesovoxel. Instead, we considered three mesovoxel designs, as shown in Fig. 4a and Supplementary Fig. 26, with varying degrees of information compression: [3,4,1] (Mesovoxel 5), [4,8,1] (Mesovoxel 6) and [4,12,1] (Mesovoxel 7). Optical and SEM imaging (Fig. 4a and Supplementary Figs. 56 and 57), in conjunction with SAXS (Fig. 4 and Supplementary Figs. 40–45), confirm that all three designs form a periodic helix-based crystal structure (space group I4122; Supplementary Fig. 54), which is achiral overall due to alternating motif arrangements within the crystal (Supplementary Fig. 55). Increasing the planar X–Y spacing between helices would yield chiral designs with an associated optical response, and will be the subject of future studies. Note that the minimal set (Mesovoxel 5) yielded larger crystals (up to ~10 μm) than the more over-prescribed Mesovoxels 6 and 7, as can be seen in SEM images in Fig. 4a and Supplementary Fig. 57 and in optical micrographs (Supplementary Fig. 56).

Fig. 4: 3D crystal from helical NP motifs.
figure 4

a, The desired helical NP motif (left) possesses 16 voxels, but three designed mesovoxels (Mesovoxels 5–7; right) with different degrees of information compression yield the target crystal. SEM images of the corresponding assemblies are shown below. b, Experimental SAXS data for three superlattices designed from Mesovoxel 5 (black), Mesovoxel 6 (blue) or Mesovoxel 7 (green) with obtained S(q) and model S(q) (red) with the associated Bragg peak locations (see Supplementary Figs. 40–45 for details and indexing). The modelled S(q) corresponds to the space group I4122 (Supplementary Fig. 54) with lattice parameters a = b = 120 nm, c = 240 nm and α = β = γ = 90° with NP filling at the following sites: (0,0,0), (1/2,0,1/4), (1/2,1/2,1/2) and (0,1/2,3/4). c, Serial-section SEM imaging provides a volumetric reconstruction of NP positions within a 3D crystal formed by Mesovoxel 7. 3D schematics of the crystal faces (left), 2D NP schematics through different faces (middle) and serial section SEM reconstructions (right), with the associated Miller indices, are shown for the designed and measured crystal organizations of helical NP motifs, which correspond to space group I4122. Scale bars, 100 nm. An SEM image of the serially sectioned silicate structures reveals long-range NP organizations over several microns throughout the interior of the crystal.

Source data

Full size image

Despite Mesovoxel 7 possessing four more chromatic bonds than Mesovoxel 6 to further lock intervoxel orientations, it does not improve crystal quality (Supplementary Fig. 26). Instead, it shows broader SAXS peaks, fewer higher-order reflections and smaller correlation lengths than Mesovoxels 5 and 6. Scherrer analysis (Supplementary Section III) confirms that more over-prescribed designs reduce crystal correlation lengths to submicrometre lengths. SAXS measurements of an empty Mesovoxel 7 crystal (Supplementary Fig. 50) show similar behaviour, indicating that the increased bond diversity is responsible for the decreased order, distinct from any influence of particles. Nevertheless, all mesovoxel designs here successfully form the intended helical-crystal superstructure, as demonstrated by SAXS and SEM and optical images (Fig. 4a and Supplementary Figs. 56 and 57) that show large crystals up to ~10 µm in size. These findings align with the experimental and modelling conclusions for the face-centred perovskite crystal (Fig. 3). A broader implication is that a higher degree of information compression is not only more effective at encoding a targeted structure, but also enhances crystal assembly. More complex mesovoxels may also benefit from tuning of the chromatic bond energies to limit defects9.

Finally, we further explored the local ordering of crystal domains using Mesovoxel 7. Although scattering provides a global view of sample crystallinity, we also studied local defects within crystal domains. We corroborated the correspondence between the assembled and designed crystal using real-space 3D imaging. Serial-section SEM imaging of a silicated structure (Fig. 4c and Supplementary Fig. 57) in conjunction with image reconstruction49 allowed us to visually decipher the hierarchical organization of helical NP motifs within the 3D crystal. We also compared the projections obtained from the 3D reconstruction with those from the targeted designed structure, revealing an assembled structure that is strikingly similar to our targeted designed organization of a repeating helical NP motif (Supplementary Videos 1 and 2).

These last two NP architectures, the nanoscale face-centred perovskite and helical NP systems, demonstrate the same trends in that the most ‘compressed’ mesovoxel provided the highest crystal quality and largest domain sizes. In the helical system, a third mesovoxel with added binding information continued this trend. Next we approach a desired optical function using a minimal mesovoxel to demonstrate the ability to generate functional materials using our inverse design approach.

Bridging plasmonic and photonic length scales with designed 3D NP crystals

There is tremendous interest in spanning multiple length scales that would enable access to plasmonic and photonic regimes for applications in light emission, information processing and light control. We used our design strategy to create 3D lattices that orthogonally align nanoscale and photonic scales to achieve a designed optical property. While plasmonic effects need spacings of tens of nanometres or smaller, photonic effects rely on features of approximately half a wavelength (that is, hundreds of nanometres). We applied our inverse design approach to assemble a structure that functions as a distributed Bragg reflector (DBR). Although such large NP spacings are traditionally difficult to achieve via self-assembly, NP-based DBRs provide enhanced tunability and versatility compared with traditional DBRs. DBRs, serving as optical mirrors, are important in the fabrication of optical cavities, which are used in devices based on enhanced light–material interactions such as light emitters50, sensors51 and modulators, and enable exciton–polaritons in 2D materials52.

To realize an optical-scale interplane spacing, we extended the spacing of the 2D Au NP planes design from Fig. 2c to include three empty voxel layers between NP-filled planes (Fig. 5a). A fully prescribed layout would require a [16,48,1] mesovoxel, but by exploiting mirror-plane symmetry at the midpoint between NP planes, we reduced this to only three-layer types (each with an in-plane external bond colour) and two bond colours in the Z direction. Consequently, a [6,5,1] mesovoxel (Mesovoxel 8) could be designed (see Supplementary Fig. 27 for details).

Fig. 5: Design of 3D NP orgnization with nanoscale (in-plane) and photonic (interplane) spacing regimes.
figure 5

a, Mesovoxel 8 is composed of six voxels utilizing five bond colours to build three distinct voxel NP planes, mirrored to create larger NP spacings. b, SAXS data for the synthesized crystal (black) versus modelled S(q) (red) with the associated indexing of Bragg peaks (Supplementary Figs. 46 and 47) and inset 2D SAXS pattern, corresponding to a tetragonal primitive lattice with lattice parameters a = b = 58.34 nm, c = 233.4 nm and α = β = γ = 90°. The inset plot is an enlargement of the scattering region beyond q = 0.01 Å, highlighting higher-order structural features. c,d, SEM images of silicated crystals. Scale bars, 2 µm (c), 1 µm (d). e, TEM image of the (100) crystal face after FIB sectioning. Scale bar, 200 nm. f, EDS scanning transmission electron microscopy (STEM) image of the same sample showing the location of Au within the structure (see Supplementary Fig. 59 for further details). g, Schematic of Bragg diffraction, where θ is the incident light angle, c is the distance between particle planes, a is the distance between in-plane particles, d is the particle diameter and neff is the background refractive index. h, Upper plot shows the mean and maximum diameters of Au NPs over growth cycles 0–3 (N = 2,508, 740, 520, 288 NPs, respectively, with error bars representing ±1 s.e.m.). Comparative optical microscope images of representative samples at NP growth cycle 0 (that is, the initial state, top) and at growth cycle 3 (bottom) are also shown (scale bars, 10 μm). The green background of the images is due to a Fabry–Pérot resonance near wavelength λ = 525 nm due the indium tin oxide glass coating, which has been subtracted from the reflectance spectra. Lower plot shows simulated (dashed line) and measured (solid lines) reflection spectra under normal incidence for particle growth cycles 0–3, showing pronounced Bragg peaks in the wavelength range of 625–650 nm. Each measured spectral curve is the average of six spectra taken from six distinct samples synthesized in the same batch. The raw spectra and additional sample images are included in Supplementary Section V.

Source data

Full size image

This design allowed us to reach the photonic regime, where the spacing between NP planes is 233.4 nm, as revealed by the SAXS measured S(q) and in-plane NP spacing of 58.3 nm (Fig. 5b and Supplementary Figs. 46 and 47). SEM images of silicated samples (Fig. 5c,d and Supplementary Fig. 58) confirm a 3D simple cubic grid with crystallites up to ~6 µm in size and multiple domains (also seen in optical images; Supplementary Fig. 58). TEM (Fig. 5e and Supplementary Figs. 58 and 59) further validates the lattice structure, revealing (100) planes with NPs spaced by three empty voxel layers—yielding a tetragonal lattice with a high aspect ratio (~4). The planes of Au NPs were also revealed by energy-dispersive X-ray spectroscopy (EDS) STEM imaging (Fig. 5f and Supplementary Fig. 59).

A simulation of the reflection spectrum from the synthesized structure is shown in Fig. 5h (dashed curve) using a ten-layer structure of Au NPs (11.5 nm) with parameters defined in Fig. 5g under normal incidence. This peak profile is heavily dependent on particle size, as shown in our modelling (Supplementary Fig. 17b) and described in Supplementary Section V. We note that a control simulation shows a negligible reflectance (<10−3).

Optical spectroscopic measurements of the Au NP-filled and silicated tetragonal lattices with progressively larger NP diameters (Fig. 5h) show pronounced Bragg peaks consistent with the design and simulated optical characteristics. It should be noted that these structures have been silicated and thus are solid-state structures possessing the desired optical properties. The diameters of the Au NPs were increased by a post-incorporation growth process (Supplementary Section II). Stronger Bragg reflection is expected for samples with larger Au NPs, and close alignment of the modelled curves and experimental results is shown in Supplementary Figs. 19 and 20, from the initial 3% reflectance for no growth to ~8.5% for the samples with the most growth cycles (Fig. 5h and Supplementary Fig. 20). Our full-wave simulations indicate that all examined samples contained approximately ten Au NP layers (spaced by c = 233.4 nm), and that those from growth cycles 0–2 had neff = 1.35, while those from growth cycle 3 had a slightly higher neff = 1.39, which can be attributed to an increased degree of silication. Crystals with larger particles showed higher reflectance, producing a clear visual difference under illumination (images of growth cycles 0 and 3; a full set of images is included in Supplementary Fig. 18a). SEM images (Supplementary Fig. 18b) confirm a highly ordered material with silica growth throughout the lattice.

These results show how our assembly strategy can organize NPs to provide a target optical function and then enhance their response through in-lattice regrowth. Full-wave simulations (Supplementary Fig. 17) indicate that further reflectance gains can be made by using larger NPs or additional particle layers—20 nm and 30 nm particles provide ~20% and ~50% increases, respectively, in the same crystal structure and ten-layer arrangement (Supplementary Fig. 17c,d). Although current voxel designs limit cargo size, the method can be adapted to other voxel geometries that accommodate larger particles. These photonic crystals could serve as passive Bragg reflectors or actively enhance spontaneous emission (for example, with quantum dots) via the Purcell effect, functioning as potential nano-lasers. By relying on self-assembly, rather than top-down fabrication, our approach offers 3D nanoscale control and seamless nanomaterial integration42. It can be extended to other self-assembled photonic metamaterials, including complete photonic bandgaps or dielectric mirrors, and their on-chip integration53.

Conclusion

We demonstrated an inverse design strategy for multi-component assembly in which a set of material voxels, or DNA objects, each with directional and DNA-encoded (chromatic) interactions, enables the hierarchical assembly of NPs into 3D architectures. By leveraging structural symmetries to minimize the numbers of voxel types and bond colours, we explored information compression as the guiding principle of the design and assembly process. Our approach is robust: different mesovoxel designs still assembled into the same overall crystal structure, albeit with variations in crystal morphology and growth pathways. We determined experimentally and computationally that a mesovoxel design with a minimal number of voxel types and chromatic bonds—that is, the highest degree of information compression required to encode the targeted hierarchical organization—results in more effective growth with larger crystalline domains and better internal organization. Future work will explore further control over assembly pathways to promote high-fidelity growth of structures and more complex morphologies. We showcased the practical utility of this assembly methodology by constructing a 3D DBR, demonstrating how inverse design can yield functional materials through our bottom-up approach. Future extensions of this work may target strategies that optimize fidelity, defect tolerance and morphology. Ultimately, this strategy paves the way for bottom-up 3D nanofabrication that could be used for diverse applications in optics, energy materials, information processing and biomaterials that rely on the precise organization of nanoscale components in prescribed 3D materials.

Methods

Design, synthesis and purification of DNA origami

The octahedral DNA origami frame was designed using the DNA origami design software caDNAano (http://cadnano.org/). The edges of the octahedral frame consist of six-helix bundles with edge lengths of 84 base pairs. Each of the six-helix bundles has one staple sequence extending from each of the ends for inter-origami binding, resulting in four ssDNA sequences extending away from each of the six vertices of the octahedron. For the capture and positioning of nanoscale components in the interior space of the origami, eight ssDNA sequences were modified to have overhangs that extend towards the interior of the origami. All DNA sequences used in this work are provided in Supplementary Sections VII and VIII and Supplementary Table 11.

DNA origami frames were folded by mixing 40 nM of M13mp18 scaffold purchased from Bayou Biolabs, LLC, with a 5:1 ratio of staples to scaffolds in a 40 mM Tris buffer (~pH 8.0) containing 1 mM EDTA and 12.5 mM MgCl2. The staple sequences were purchased from Integrated DNA Technologies. This mixture was heated to 90 °C and slowly cooled to 25 °C over a period of 20 h to allow the correct folding of the scaffold sequence into the target 3D DNA origami frame. The folded DNA origami samples were washed five times to remove excess staples through Millipore Sigma Amicon Ultra-0.5 ml (100 kDa) centrifugal filters in an Eppendorf 5424R at a speed of 500 r.c.f. for 25 min using a buffer consisting of 1× tris-acetate-EDTA buffer with 12.5 mM MgCl2.

Preparation of DNA-functionalized Au NPs

Thiolated oligonucleotides, also purchased from IDT, were reduced by tris[2-carboxyethyl] phosphine at a 100× molar excess to particles. Au NPs with a diameter of 10 nm, purchased from Ted Pella Inc., were mixed with the thiolated oligonucleotides at a ratio of 1:300 under gentle shaking. The mixture was buffered to a 10 mM phosphate buffer (~pH 7.0) after a 1.5 h room-temperature incubation. After another 1.5 h incubation, the sodium chloride concentration was slowly brought up to 300 mM over 250 min and then aged at room temperature overnight (or for at least 12 h). The functionalized Au NPs were washed five times with deionized water using an Eppendorf 5424R at a speed of 21,130 r.c.f. to remove the excess thiolated sequences and salts.

Preparation of superlattice samples

All origami required for a given mesovoxel design (at the required molar ratios) were mixed in solution. Au NPs were then added to this mixture at a 2× molar excess to the number of binding sites (internal spaces meant to host NPs). The mixture was heated to 50 °C and slowly cooled to 25 °C over 5 days at a rate of −0.2 °C h−1. This annealing was performed in separate PCR tubes but could also be performed in microwell plates.

Pre-loading of origami with DNA-functionalized Au NPs

To ensure that a greater percentage of NPs were loaded into the superlattices for Mesovoxel 7 (for 3D reconstruction, shown in Fig. 4), the origami designed to capture the NPs were first annealed with a 4× excess of DNA-functionalized Au NPs. These pre-loaded origami were mixed with the other DNA origami and then annealed according to the protocol described in ‘Preparation of superlattice samples’. The pre-loading annealing protocol was as follows: hold at 50 °C for 5 min, ramp of −0.2 °C h−1 to 40 °C, hold at 40 °C for 5 min, ramp of −0.6 °C h−1 to 25 °C and finally hold at 25 °C for 2 min.

Silication of DNA–NP superlattices

DNA origami superlattices were coated with robust silica through a sol–gel procedure for subsequent visualization with SEM/TEM. For conversion to inorganic silica, superlattices were centrifuged briefly in an Eppendorf 5424R at 1,000 r.c.f. for 30 s, and buffer exchanged with 1× tris-acetate buffer (~pH 8.0) with 10 mM magnesium acetate (Mg(OAc)2).

The sol–gel solution was prepared with 0.2–0.5% 3-aminopropyl-triethoxysilane (APTES) and a 0.7–2% solution of tetraethoxysilane in 1× tris-acetate buffer with 10 mM Mg(OAc)2. The APTES was added first, followed immediately by tetraethoxysilane, which was then mixed vigorously at 500–800 r.p.m. on a shaker for 25–30 min. The solution was filtered with Millex-GV PVDF 0.22 µm filters, then 15 µl of the filtered solution was mixed with 5 µl of superlattice and placed back onto a shaker at 700 r.p.m. for 1–1.5 h. The reaction was stopped by adding deionized water or 1× tris-acetate buffer, followed by further exchanging of the supernatant two times with deionized water after brief spin-downs. The silica–superlattice conjugate was drop-casted onto a silicon chip substrate for observation by SEM or onto a 300 mesh TEM grid for TEM.

A surface-based silication protocol was used for the Bragg reflector samples (Fig. 5). First, indium tin oxide (ITO) glass was cleaned with deionized water and isopropyl alcohol, then dried. Plasma was used to discharge the ITO surface for 5 min. Next, 4 µl of lattice solution was added onto a 3 mm × 3 mm piece of ITO glass, followed by 2 µl of tris-acetate-EDTA buffer. Separately, a PCR tube with 250 µl of silication solution was prepared, consisting of 445 µl deionized water and 50 µl 10× carbonate–bicarbonate buffer. Immediately before placing the ITO glass into the PCR tube, 1 µl APTES and 3.5 µl tetraethoxysilane were added. The glass was then placed inside the PCR tube and shaken on a thermomixer at 550 r.p.m. (maintained at 25° C) for 1 h. After silication, the ITO was cleaned with deionized water and dried at 120 °C on a thermoplate until the water evaporated.

Au growth

Samples that required large NPs to increase visibility under electron microscopy (Mesovoxel 7) were grown using GoldEnhance EM Plus at a volume ratio of approximately 1:10 (GoldEnhance:DNA lattice + buffer) for 15 min. The reaction was ended by 3× buffer exchange with deionized water or buffer depending on the sample. For example, a typical recipe was as follows: 2 µl of premixed GoldEnhance EM Plus solution was added to a solution of 20 µl deionized water and 2 µl of approximately 20 nM superlattice. The solution was vortexed to ensure sufficient mixing and incubated for 15 min. The sample visibly changed from red to dark purple or black depending on the concentration or time of incubation. An additional 2 µl (approximately 10% by volume) would result in Au NPs with approximately 15–20 nm diameters. For certain samples, where the effect of multiple rounds of Au NP growth was studied, the protocol was to mix 1 µl for every 10 µl of Au NP-filled DNA lattice solution and set to 25 °C, then mix at 350 r.p.m. for 5 min. This was repeated for as many cycles of Au NP growth as desired; when completed, the sample was buffer exchanged into 1× tris-acetate-EDTA and 12.5 mM MgCl2.

Sample preparation for SEM, TEM and STEM

Samples were drop-casted from the solution to either silicon wafers or 300 mesh TEM grids and dried at room temperature for observation under SEM and TEM. SEM was performed using a Hitachi 4800 SEM; typical operating conditions were 3 keV and a 7–10 nA current. TEM was performed using a JEOL 1400 operated at 120 keV. STEM EDS (Fig. 5f) was performed using an FEI Talos F200X, typically operated at 200 keV.

Serial-section TEM, STEM and EDS

TEM cross-sectional samples (TEM lamellae) were prepared using the in situ lift-out method in a Helios 600 dualbeam FIB with final Ga+ milling at 5 keV to reduce beam damage. For the bright-field TEM images used in Figs. 2e (bottom) and 3c, the greyscale was roughly inversely proportional to the density of the sample material (vacuum is white and Au would be black). For high-angle annular dark-field STEM images used in Fig. 5, the greyscale is proportional to atomic number (for example Au is white). EDS acquisitions, shown in Fig. 5f, were captured in high-angle annular dark-field STEM mode.

Serial-section SEM

DNA–NP superlattices were drop-casted onto clean silicon wafers. Imaging and serial sectioning were performed using the FEI Helios Nanolab 660 SEM/FIB; Auto Slice and View G3 software suites were used to automate collection. The particle cluster was imaged with an Elstar in-lens BSE detector (TLD-BSE) at 5 keV with a 10 µs dwell time and a 100 pA current. A sacrificial layer of Pt was deposited on top of the sample to help avoid the sample being damaged before slicing, after which a trench was milled surrounding the sample and a fiducial marker was placed with Pt for Auto Slice and view functionality. The FIB current was set to 0.24 nA at 30 keV, and a 10 nm step size was selected for layer removal. A total of 162 slices were collected using this method. The Dragonfly ORS software was used to perform corrections and to filter and view data.

SAXS characterization

SAXS measurements were performed at the Complex Materials Scattering and Soft Matter Interfaces beamlines at the National Synchrotron Light Source II at Brookhaven National Laboratory in Upton, NY. The 2D scattering data were collected on area detectors located downstream of the sample position. Further workstation information is provided in Supplementary Table 2. All raw scattering data for Figs. 2–5 are included in Source data Figs. 2–5.

Dynamic light scattering

The dynamic light scattering measurements were conducted using a Malvern Zetasizer ZS instrument at a backscattering angle of 173°. This instrument was equipped with a 633 nm laser source and a backscattering detector.

Optical characterization

We used a custom-built microscope equipped with a ×100 Nikon Objective (numerical aperture = 0.85) to acquire sample images and reflection spectra. A laser beam from a supercontinuum source (NKT Photonics SuperK Extreme) was shone perpendicularly onto the top surface of the sample being characterized through the objective. The reflected light was collected through the same objective and analysed using a visible spectrometer (Ocean Optics USB2000+). All of the reflection spectra were normalized against that of a silver mirror.