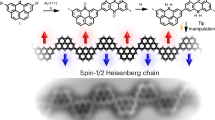
Abstract
Unlocking the potential of topological order in many-body spin systems has been a key goal in quantum materials research. Despite extensive efforts, the quest for a versatile platform enabling site-selective spin manipulation, essential for tuning and probing diverse topological phases, has persisted. Here we utilize on-surface synthesis to construct spin-1/2 alternating-exchange Heisenberg chains by covalently linking Clar’s goblets—nanographenes each hosting two antiferromagnetically coupled spins. Using scanning tunnelling microscopy, we exert atomic-scale control over chain lengths, parities and exchange-coupling terminations, and probe their magnetic response via inelastic tunnelling spectroscopy. Our investigation confirms the gapped nature of bulk excitations in the chains, known as triplons. Their dispersion relation is extracted from the spatial variation of tunnelling spectral amplitudes. Depending on the parity and termination of chains, we observe varying numbers of in-gap spin-1/2 edge excitations, reflecting the degeneracy of distinct topological ground states in the thermodynamic limit. By monitoring interactions between these edge spins, we identify the exponential decay of spin correlations. Our findings present a phase-controlled many-body platform, opening avenues toward spin-based quantum devices.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available on the Materials Cloud platform via https://doi.org/10.24435/materialscloud:x8-7y (ref. 60).
Code availability
All relevant codes are available on the Materials Cloud platform via https://doi.org/10.24435/materialscloud:x8-7y (ref. 60).
References
Kiczynski, M. et al. Engineering topological states in atom-based semiconductor quantum dots. Nature 606, 694–699 (2022).
Sompet, P. et al. Realizing the symmetry-protected Haldane phase in Fermi–Hubbard ladders. Nature 606, 484–488 (2022).
Mishra, S. et al. Observation of fractional edge excitations in nanographene spin chains. Nature 598, 287–292 (2021).
Wang, H. et al. Construction of topological quantum magnets from atomic spins on surfaces. Nat. Nanotechnol. https://doi.org/10.1038/s41565-024-01775-2 (2024).
Xie, Y. et al. Fractional Chern insulators in magic-angle twisted bilayer graphene. Nature 600, 439–443 (2021).
Trebst, S. & Hickey, C. Kitaev materials. Phys. Rep. 950, 1–37 (2022).
Dzero, M., Sun, K., Galitski, V. & Coleman, P. Topological Kondo insulators. Phys. Rev. Lett. 104, 106408 (2010).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Savary, L. & Balents, L. Quantum spin liquids: a review. Rep. Prog. Phys. 80, 016502 (2016).
Zhou, Y., Kanoda, K. & Ng, T.-K. Quantum spin liquid states. Rev. Mod. Phys. 89, 025003 (2017).
Grohol, D. et al. Spin chirality on a two-dimensional frustrated lattice. Nat. Mater. 4, 323–328 (2005).
Su, W., Schrieffer, J. & Heeger, A. J. Solitons in polyacetylene. Phys. Rev. Lett. 42, 1698–1701 (1979).
Hida, K. Crossover between the Haldane-gap phase and the dimer phase in the spin-1/2 alternating Heisenberg chain. Phys. Rev. B 45, 2207–2212 (1992).
Chen, X., Gu, Z.-C. & Wen, X.-G. Classification of gapped symmetric phases in one-dimensional spin systems. Phys. Rev. B 83, 035107 (2011).
Nakamura, M. & Todo, S. Order parameter to characterize valence-bond-solid states in quantum spin chains. Phys. Rev. Lett. 89, 077204 (2002).
Balents, L. Spin liquids in frustrated magnets. Nature 464, 199–208 (2010).
Drost, R., Kezilebieke, S., Lado, J. L. & Liljeroth, P. Real-space imaging of triplon excitations in engineered quantum magnets. Phys. Rev. Lett. 131, 086701 (2023).
Diederix, K., Blöte, H., Groen, J., Klaassen, T. & Poulis, N. Theoretical and experimental study of the magnetic properties of the singlet-ground-state system Cu(NO3)2·2.5H2O: an alternating linear Heisenberg antiferromagnet. Phys. Rev. B 19, 420–431 (1979).
Bonner, J. C., Friedberg, S. A., Kobayashi, H., Meier, D. L. & Blöte, H. W. Alternating linear-chain antiferromagnetism in copper nitrate Cu(NO3)2·2.5H2O. Phys. Rev. B 27, 248–260 (1983).
Garrett, A., Nagler, S., Tennant, D., Sales, B. & Barnes, T. Magnetic excitations in the S = 1/2 alternating chain compound (VO)2P2O7. Phys. Rev. Lett. 79, 745–748 (1997).
Forsyth, J., Wilkinson, C. & Zvyagin, A. The antiferromagnetic structure of copper tungstate, CuWO4. J. Phys. Condens. Matter 3, 8433 (1991).
Lake, B., Cowley, R. & Tennant, D. A dimer theory of the magnetic excitations in the ordered phase of the alternating-chain compound. J. Phys. Condens. Matter 9, 10951 (1997).
Waki, T. et al. Observation of Bose–Einstein condensation of triplons in quasi 1D spin-gap system Pb2V3O9. J. Phys. Soc. Jpn 73, 3435–3438 (2004).
Valentine, J., Silverstein, A. & Soos, Z. Interdimer exchange in linear chain copper acetate-pyrazine. J. Am. Chem. Soc. 96, 97–103 (1974).
Bray, J. et al. Observation of a spin-Peierls transition in a Heisenberg antiferromagnetic linear-chain system. Phys. Rev. Lett. 35, 744–747 (1975).
Jacobs, I. et al. Spin-Peierls transitions in magnetic donor–acceptor compounds of tetrathiafulvalene (TTF) with bisdithiolene metal complexes. Phys. Rev. B 14, 3036–3051 (1976).
Castilla, G., Chakravarty, S. & Emery, V. Quantum magnetism of CuGeO3. Phys. Rev. Lett. 75, 1823–1826 (1995).
Riera, J. & Dobry, A. Magnetic susceptibility in the spin-Peierls system CuGeO3. Phys. Rev. B 51, 16098–16102 (1995).
Hase, M., Terasaki, I. & Uchinokura, K. Observation of the spin-Peierls transition in linear Cu2+ (spin-1/2) chains in an inorganic compound CuGeO3. Phys. Rev.Lett. 70, 3651–3654 (1993).
Cai, J. et al. Atomically precise bottom-up fabrication of graphene nanoribbons. Nature 466, 470–473 (2010).
Ruffieux, P. et al. On-surface synthesis of graphene nanoribbons with zigzag edge topology. Nature 531, 489–492 (2016).
Rizzo, D. J. et al. Topological band engineering of graphene nanoribbons. Nature 560, 204–208 (2018).
Blackwell, R. E. et al. Spin splitting of dopant edge state in magnetic zigzag graphene nanoribbons. Nature 600, 647–652 (2021).
Ortiz, R. et al. Exchange rules for diradical π-conjugated hydrocarbons. Nano Lett. 19, 5991–5997 (2019).
Mishra, S. et al. Topological frustration induces unconventional magnetism in a nanographene. Nat. Nanotechnol. 15, 22–28 (2020).
Mishra, S. et al. Large magnetic exchange coupling in rhombus-shaped nanographenes with zigzag periphery. Nat. Chem. 13, 581–586 (2021).
Cheng, S. et al. On-surface synthesis of triangulene trimers via dehydration reaction. Nat. Commun. 13, 1705 (2022).
Wang, T. et al. Aza-triangulene: on-surface synthesis and electronic and magnetic properties. J. Am. Chem. Soc. 144, 4522–4529 (2022).
Madhavan, V., Chen, W., Jamneala, T., Crommie, M. & Wingreen, N. Tunneling into a single magnetic atom: spectroscopic evidence of the Kondo resonance. Science 280, 567–569 (1998).
Hirjibehedin, C. F., Lutz, C. P. & Heinrich, A. J. Spin coupling in engineered atomic structures. Science 312, 1021–1024 (2006).
Zhao, C. et al. Tailoring magnetism of graphene nanoflakes via tip-controlled dehydrogenation. Phys. Rev. Lett. 132, 046201 (2024).
Krane, N. et al. Exchange interactions and intermolecular hybridization in a spin-1/2 nanographene dimer. Nano Lett. 23, 9353–9359 (2023).
Lado, J. L. & Fernández-Rossier, J. Magnetic edge anisotropy in graphenelike honeycomb crystals. Phys. Rev. Lett. 113, 027203 (2014).
Fernández-Rossier, J. Theory of single-spin inelastic tunneling spectroscopy. Phys. Rev. Lett. 102, 256802 (2009).
Ternes, M. Spin excitations and correlations in scanning tunneling spectroscopy. New J. Phys. 17, 063016 (2015).
White, S. R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 69, 2863 (1992).
Wang, H. T., Li, B. & Cho, S. Y. Topological quantum phase transition in bond-alternating spin-1/2 Heisenberg chains. Phys. Rev. B 87, 054402 (2013).
Collins, A., Hamer, C. J. & Weihong, Z. Modified triplet-wave expansion method applied to the alternating Heisenberg chain. Phys. Rev. B 74, 144414 (2006).
Ochsenbein, S. et al. Standing spin waves in an antiferromagnetic molecular Cr6 horseshoe. Europhys. Lett. 79, 17003 (2007).
Shannon, C. Communication in the presence of noise. Proc. IRE 37, 10–21 (1949).
Salace, G., Petit, C. & Vuillaume, D. Inelastic electron tunneling spectroscopy: capabilities and limitations in metal–oxide–semiconductor devices. J. Appl. Phys. 91, 5896–5901 (2002).
Kennedy, T. Exact diagonalisations of open spin-1 chains. J. Phys. Condens. Matter 2, 5737 (1990).
Barnes, T., Riera, J. & Tennant, D. S=1/2 alternating chain using multiprecision methods. Phys. Rev. B 59, 11384–11397 (1999).
Baumann, S. et al. Electron paramagnetic resonance of individual atoms on a surface. Science 350, 417–420 (2015).
Jacob, D. & Fernández-Rossier, J. Theory of intermolecular exchange in coupled spin-1/2 nanographenes. Phys. Rev. B 106, 205405 (2022).
Fishman, M., White, S. R. & Stoudenmire, E. M. The ITensor software library for tensor network calculations. SciPost Phys. Codebases 10.21468/SciPostPhysCodeb.4 (2022).
Appelbaum, J. A. Exchange model of zero-bias tunneling anomalies. Phys. Rev. 154, 633–643 (1967).
Weinberg, P. & Bukov, M. QuSpin: a Python package for dynamics and exact diagonalisation of quantum many body systems part I: spin chains. SciPost Phys. 2, 003 (2017).
Zhao, C. et al. Tunable topological phases in nanographene-based spin-1/2 alternating-exchange Heisenberg chains. Materials Cloud Archive https://doi.org/10.24435/materialscloud:x8-7y (2024).
Acknowledgements
We thank S. Mishra for critical reading of the manuscript. This work was supported by the Swiss National Science Foundation (grant numbers 212875 (R.F.), CRSII5_205987 (P.R., J.F.-R.)), an ERC Consolidator grant (T2DCP, grant number 819698 (X.F.)), the Center for Advancing Electronics Dresden (cfaed) (X.F.), H2020-EU.1.2.2.-FET Proactive Grant (LIGHT-CAP, 101017821 (X.F.)), the DFG-SNSF Joint Switzerland-German Research Project (EnhanTopo, number 429265950 (P.R., X.F.)), the European Union (grant FUNLAYERS-101079184 (J.F.-R., X.F.)), the Fundação para a Ciência e a Tecnologia (grant number PTDC/FIS-MAC/2045/2021 (J.F.-R.)), Generalitat Valenciana (grant number Prometeo2021/017 (J.F.-R.)), MICIN-Spain (grant numbers PID2019-109539GB-C41 and PID2022-141712NB-C22 (J.F.-R.)) and the Advanced Materials programme supported by MCIN with funding from European Union NextGenerationEU (PRTR-C17.I1 (J.F.-R.)). We also greatly appreciate financial support from the Werner Siemens Foundation (CarboQuant (R.F., O.G.)).
Author information
Authors and Affiliations
Contributions
X.F., P.R. and R.F. conceived the project. J.-J.Z. and L.Y. synthesized and characterized the precursor molecules in solution, with supervision provided by J.M. C.Z. and L.Y. performed the on-surface synthesis. C.Z. performed the STM/STS measurements and analysed the data. G.C., J.C.G.H. and J.F.-R. performed the CAS, ED and DMRG calculations. C.Z., G.C., O.G., P.R., J.F.-R. and R.F. interpreted the Fourier analysis to triplon excitation. C.Z., G.C., J.F.-R. and R.F. wrote the manuscript. All authors discussed the results.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Nanotechnology thanks David Serrate, Ping Yu and Fangzhou Zhao for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 On-surface synthesis.
Schematic drawing for the on-surface synthesis of goblet chains from the precursor to the ribbon.
Extended Data Fig. 2 Exchange couplings involved in the goblet chain system.
a, Topographic image of a modified mirror-symmetric dimer containing only the nearest inter-goblet coupling Jinter. Vbias = 100 mV, Iset = 500 pA. The dI/dV spectra taken at different spin sites are displayed in the right panel (Iset = 500 pA), with the averaged d2I/dV 2 spectrum represented as a light brown curve. b, Topographic image of a modified dimer containing only the second nearest inter-goblet coupling Jnn. Vbias = − 50 mV, Iset = 500 pA. The dI/dV spectra taken at different spin sites are displayed in the right panel (Iset = 500 pA). c, Topographic image of a modified dimer containing only the third nearest inter-goblet coupling Jnnn. Vbias = − 50 mV, Iset = 500 pA. The dI/dV spectra taken at various spin sites are displayed in the right panel (Iset = 800 pA). d, Topographic image of an engineered dimer containing Jintra, Jnn, and Jnnn. Vbias = − 50 mV, Iset = 300 pA. The corresponding dI/dV spectra are also shown in the right panel, with the averaged d2I/dV 2 spectrum of 3 and 4 represented as a light brown curve. All white scale bars denote 0.5 nm. The background spectra taken on the Au(111) substrate are shown as references. All dI/dV spectra are taken with Vrms = 2 mV.
Extended Data Fig. 3 CAS calculation for determining intra/inter-goblet exchange couplings.
a, Excitation energy from the singlet ground state to the triplet excited states of a goblet monomer, as a function of U/t1, for t3 = 0.07t1, where U is the on-site Coulomb repulsion, t1 = 2.7 eV is the hopping parameter for the nearest carbon sites and t3 is the third-neighbour hopping. The parameters that fit the experimental results are found to be U/t1 ~ 0.7. b, Eigenvalues of the ground and the first several excited states for a goblet monomer using the optimized parameters. c-f, Eigenvalues of the ground and the first several excited states for modified goblet dimers having only J2 coupling (inversion symmetric), J2 coupling (mirror symmetric), Jnn coupling, and Jnnn coupling, respectively.
Extended Data Fig. 4 Calculated eigenstate energies by exact diagonalization of chains shown in Fig. 2 in the main text.
a, J1-terminated chain with L = 22. b, J2-terminated chain with L = 20.
Extended Data Fig. 5 Calculated excitation energies and probabilities from the ground state to various triplon modes.
Calculated excitation energies and probabilities from the ground state to various triplon modes of an L = 20 odd-Haldane chain through single-site excitation. Different α values are considered (α = J1/J2). The probability is obtained by summing up the corresponding spin spectral weight of all sites along the chain and is represented by the size of the marker. The one-triplon branch is roughly symmetric around J2 and the bandwidth increases with J1, suggesting that a non-zero J1 is the origin of the dispersive triplon.
Extended Data Fig. 6 Bulk and edge dI/dV spectra, for chains with different lengths L.
Bulk (average of spin sites No. L/2 and No. L/2 + 1 in the middle) and edge (average of spin sites No. 1 and No. L at the ends) dI/dV spectra, for chains with different lengths L. For all the dI/dV spectra: Iset = 500 pA, Vrms = 2 mV. The corresponding d2I/dV 2 are also shown aside. Detailed experimental data for chains with L = 4–12, 16, 24 and 26 are in Supplementary Fig. 6, for L = 14 and 18 in Extended Data Fig. 7, for L = 28 in Supplementary Fig. 8, and for L = 40 in Supplementary Fig. 5.
Extended Data Fig. 7 Selective spin activation along a chain.
a-e, Schematic illustration, STM topographic image, and dI/dV spectra taken on activated spin sites during the step-by-step activation described in Fig. 4e-g of the main text. The background spectra taken on the Au substrate are shown by grey curves. All STM images are taken with a CO-functionalized tip: Vbias = − 100 mV, Iset = 100 pA. All spectra are taken with: Iset = 500 pA, Vrms = 2 mV. f and g, ZBC extracted from \(7+1/2\) and \(8+1/2\) chains, which have mixed terminations.
Extended Data Fig. 8 Comparison between dehydrogenative and hydrogenative passivation of spin sites.
a, Schematic illustration of different engineering methods for spin manipulation. b and c, Schematic illustration and topographic image of a dehydrogenative passivated goblet dimer containing only J2. Vbias = 100 mV, Iset = 500 pA. d and e, Schematic illustration and topographic image of a hydrogenative passivated goblet dimer containing only J2. Vbias = − 45 mV, Iset = 500 pA. f, The corresponding dI/dV spectra taken in c and e. Iset = 800 pA. The averaged d2I/dV2 spectra of 1 (5) and 2 (6) are shown in the bottom panel. All dI/dV spectra are taken with Vrms = 2 mV. Scale bars denote 0.5 nm.
Supplementary information
Supplementary Information
Supplementary Notes containing Supplementary Figs. 1–22 with related discussions.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zhao, C., Catarina, G., Zhang, JJ. et al. Tunable topological phases in nanographene-based spin-1/2 alternating-exchange Heisenberg chains. Nat. Nanotechnol. 19, 1789–1795 (2024). https://doi.org/10.1038/s41565-024-01805-z
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41565-024-01805-z
This article is cited by
-
Fabrication of spin-1/2 Heisenberg antiferromagnetic chains via combined on-surface synthesis and reduction for spinon detection
Nature Synthesis (2025)
-
Solution-phase synthesis of Clar’s goblet and elucidation of its spin properties
Nature Chemistry (2025)
-
Spin-1/2 Heisenberg chains realized in π-electron systems
Nature Synthesis (2025)
-
Spin excitations in nanographene-based antiferromagnetic spin-1/2 Heisenberg chains
Nature Materials (2025)
-
Unravelling topological states in quantum spin chains
Nature Nanotechnology (2024)