Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Maximum tolerable excess noise in continuous-variable quantum key distribution and improved lower bound on two-way capacities

Nature Photonics volume 19, pages 329–334 (2025)Cite this article

Subjects

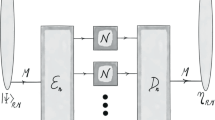
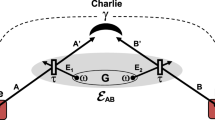
Abstract

The two-way capacities of quantum channels determine the ultimate entanglement and secret-key distribution rates achievable by two distant parties that are connected by a noisy transmission line, in the absence of quantum repeaters. Since repeaters will likely be expensive to build and maintain, a central open problem of quantum communication is to understand what performances are achievable without them. Here we find a new lower bound on the energy-constrained and unconstrained two-way quantum and secret-key capacities of all phase-insensitive bosonic Gaussian channels, namely thermal attenuator, thermal amplifier and additive Gaussian noise, which are realistic models for the noise affecting optical fibres or free-space links. Ours is the first non-zero lower bound on the two-way quantum capacity in the parameter range where the (reverse) coherent information becomes negative, and it shows explicitly that entanglement distribution is always possible when the channel is not entanglement breaking. This completely solves a crucial open problem of the field, namely establishing the maximum excess noise, which is tolerable in continuous-variable quantum key distribution. In addition, our construction is fully explicit; that is, we devise and optimize a concrete entanglement distribution and distillation protocol that works by combining recurrence and hashing protocols.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Bounds on the two-way capacities of the thermal attenuator, thermal amplifier and additive Gaussian noise.

Similar content being viewed by others

Data availability

No data sets were generated during this study.

References

  1. Bennett, C. H. & Bassard, G. Quantum cryptography: public key distribution and coin tossing. Theor. Comput. Sci. 560, 7–11 (2014).

    MathSciNet  MATH  Google Scholar 

  2. Serafini, A. Quantum Continuous Variables: A Primer of Theoretical Methods (CRC Press, 2017).

    MATH  Google Scholar 

  3. Grosshans, F. & Grangier, P. Continuous variable quantum cryptography using coherent states. Phys. Rev. Lett. 88, 057902 (2002).

    ADS  MATH  Google Scholar 

  4. Pirandola, S. et al. Advances in quantum cryptography. Adv. Opt. Photonics 12, 1012–1236 (2020).

    ADS  MATH  Google Scholar 

  5. Laudenbach, F. et al. Continuous-variable quantum key distribution with Gaussian modulation—the theory of practical implementations. Adv. Quantum Technol. 1, 1800011 (2018).

    MATH  Google Scholar 

  6. Zhang, Y. et al. Long-distance continuous-variable quantum key distribution over 202.81 km of fiber. Phys. Rev. Lett. 125, 010502 (2020).

    ADS  MATH  Google Scholar 

  7. Hajomer, A. A. E. et al. Long-distance continuous-variable quantum key distribution over 100-km fiber with local local oscillator. Sci. Adv. 10, eadi9474 (2024).

    Google Scholar 

  8. Zhang, Y. et al. Continuous-variable QKD over 50 km commercial fiber. Quantum Sci. Technol. 4, 035006 (2019).

    ADS  Google Scholar 

  9. Pi, Y. et al. Sub-mbps key-rate continuous-variable quantum key distribution with local local oscillator over 100-km fiber. Opt. Lett. 48, 1766–1769 (2023).

    ADS  MATH  Google Scholar 

  10. Huang, D., Huang, P., Lin, D. & Zeng, G. Long-distance continuous-variable quantum key distribution by controlling excess noise. Sci. Rep. 6, 19201 (2016).

    ADS  MATH  Google Scholar 

  11. Wehner, S., Elkouss, D. & Hanson, R. Quantum internet: a vision for the road ahead. Science 362, eaam9288 (2018).

    ADS  MathSciNet  MATH  Google Scholar 

  12. Pirandola, S. et al. Theory of channel simulation and bounds for private communication. Quantum Sci. Technol. 3, 035009 (2018).

    ADS  MATH  Google Scholar 

  13. Wilde, M. M. Quantum Information Theory 2nd edn (Cambridge Univ. Press, 2017).

  14. Khatri, S. & Wilde, M. M. Principles of quantum communication theory: a modern approach. Preprint at https://arxiv.org/abs/2011.04672 (2020).

  15. Davis, N., Shirokov, M. E. & Wilde, M. M. Energy-constrained two-way assisted private and quantum capacities of quantum channels. Phys. Rev. A 97, 062310 (2018).

    ADS  MATH  Google Scholar 

  16. Ekert, A. K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991).

    ADS  MathSciNet  MATH  Google Scholar 

  17. Pirandola, S., Laurenza, R., Ottaviani, C. & Banchi, L. Fundamental limits of repeaterless quantum communications. Nat. Commun. 8, 15043 (2017).

    ADS  MATH  Google Scholar 

  18. Briegel, H.-J., Dür, W., Cirac, J. I. & Zoller, P. Quantum repeaters: the role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998).

    ADS  MATH  Google Scholar 

  19. Munro, W. J., Azuma, K., Tamaki, K. & Nemoto, K. Inside quantum repeaters. IEEE J. Sel. Top. Quantum Electron. 21, 78–90 (2015).

    ADS  MATH  Google Scholar 

  20. Goodenough, K., Elkouss, D. & Wehner, S. Assessing the performance of quantum repeaters for all phase-insensitive Gaussian bosonic channels. New J. Phys. 18, 063005 (2016).

    ADS  MATH  Google Scholar 

  21. Takeoka, M., Guha, S. & Wilde, M. M. Fundamental rate-loss tradeoff for optical quantum key distribution. Nat. Commun. 5, 5235 (2014).

    ADS  MATH  Google Scholar 

  22. Holevo, A. S. & Werner, R. F. Evaluating capacities of bosonic Gaussian channels. Phys. Rev. A 63, 032312 (2001).

    ADS  MATH  Google Scholar 

  23. Wilde, M. M., Tomamichel, M. & Berta, M. Converse bounds for private communication over quantum channels. IEEE Trans. Inf. Theory 63, 1792–1817 (2017).

    MathSciNet  MATH  Google Scholar 

  24. Takeoka, M., Guha, S. & Wilde, M. M. The squashed entanglement of a quantum channel. IEEE Trans. Inf. Theory 60, 4987–4998 (2014).

    MathSciNet  MATH  Google Scholar 

  25. Pirandola, S., García-Patrón, R., Braunstein, S. L. & Lloyd, S. Direct and reverse secret-key capacities of a quantum channel. Phys. Rev. Lett. 102, 050503 (2009).

    ADS  MathSciNet  MATH  Google Scholar 

  26. Noh, K., Pirandola, S. & Jiang, L. Enhanced energy-constrained quantum communication over bosonic Gaussian channels. Nat. Commun. 11, 457 (2020).

    ADS  MATH  Google Scholar 

  27. Ottaviani, C. et al. Secret key capacity of the thermal-loss channel: improving the lower bound. In Proc. Quantum Information Science and Technology II (eds Gruneisen, M. T. et al.) 999609 (SPIE, 2016).

  28. Tamura, Y. et al. The first 0.14-db/km loss optical fiber and its impact on submarine transmission. J. Lightwave Technol. 36, 44–49 (2018).

    ADS  MATH  Google Scholar 

  29. Li, M.-J. & Hayashi, T. in Optical Fiber Telecommunications VII (ed. Willner, A. E.) 3–50 (Academic, 2020).

  30. Peres, A. Separability criterion for density matrices. Phys. Rev. Lett. 77, 1413–1415 (1996).

    ADS  MathSciNet  MATH  Google Scholar 

  31. Simon, R. Peres–Horodecki separability criterion for continuous variable systems. Phys. Rev. Lett. 84, 2726–2729 (2000).

    ADS  MATH  Google Scholar 

  32. Giedke, G., Kraus, B., Lewenstein, M. & Cirac, J. I. Entanglement criteria for all bipartite Gaussian states. Phys. Rev. Lett. 87, 167904 (2001).

    ADS  MATH  Google Scholar 

  33. Holevo, A. S. & Giovannetti, V. Quantum channels and their entropic characteristics. Rep. Prog. Phys. 75, 046001 (2012).

    ADS  MathSciNet  MATH  Google Scholar 

  34. Holevo, A. S. Entanglement-breaking channels in infinite dimensions. Probl. Inf. Transm. 44, 171–184 (2008).

    MathSciNet  MATH  Google Scholar 

  35. Pirandola, S. Limits and security of free-space quantum communications. Phys. Rev. Res. 3, 013279 (2021).

    MATH  Google Scholar 

  36. Wang, G., Ottaviani, C., Guo, H. & Pirandola, S. Improving the lower bound to the secret-key capacity of the thermal amplifier channel. Eur. Phys. J. D 73, 17 (2019).

    ADS  MATH  Google Scholar 

  37. Devetak, I. & Winter, A. Distillation of secret key and entanglement from quantum states. Proc. R. Soc. A 461, 207–235 (2005).

    ADS  MathSciNet  MATH  Google Scholar 

  38. Dür, H. & Briegel, H. J. Entanglement purification and quantum error correction. Rep. Prog. Phys. 70, 1381–1424 (2007).

    ADS  MathSciNet  MATH  Google Scholar 

  39. Bennett, C. H., DiVincenzo, D. P., Smolin, J. A. & Wootters, W. K. Mixed-state entanglement and quantum error correction. Phys. Rev. A 54, 3824–3851 (1996).

    ADS  MathSciNet  MATH  Google Scholar 

  40. Bennett, C. H. et al. Purification of noisy entanglement and faithful teleportation via noisy channels. Phys. Rev. Lett. 76, 722–725 (1996).

    ADS  MATH  Google Scholar 

  41. Miguel-Ramiro, J. & Dür, W. Efficient entanglement purification protocols for d-level systems. Phys. Rev. A 98, 042309 (2018).

    ADS  MATH  Google Scholar 

  42. Vollbrecht, K. G. H. & Verstraete, F. Interpolation of recurrence and hashing entanglement distillation protocols. Phys. Rev. A 71, 062325 (2005).

    ADS  MATH  Google Scholar 

  43. Sanders, B. C. Quantum dynamics of the nonlinear rotator and the effects of continual spin measurement. Phys. Rev. A 40, 2417–2427 (1989).

    ADS  MATH  Google Scholar 

  44. Winnel, M. S., Guanzon, J. J., Hosseinidehaj, N. & Ralph, T. C. Achieving the ultimate end-to-end rates of lossy quantum communication networks. npj Quantum Inf. 8, 129 (2022).

    ADS  Google Scholar 

  45. Kalb, N. N. et al. Entanglement distillation between solid-state quantum network nodes. Science 356, 928–932 (2017).

    ADS  MathSciNet  MATH  Google Scholar 

  46. Hu, X.-M. et al. Long-distance entanglement purification for quantum communication. Phys. Rev. Lett. 126, 010503 (2021).

    ADS  Google Scholar 

  47. Ecker, S. et al. Experimental single-copy entanglement distillation. Phys. Rev. Lett. 127, 040506 (2021).

    ADS  Google Scholar 

  48. Deutsch, D. et al. Quantum privacy amplification and the security of quantum cryptography over noisy channels. Phys. Rev. Lett. 77, 2818–2821 (1996).

    ADS  MATH  Google Scholar 

  49. Dehaene, J., Van den Nest, M., De Moor, B. & Verstraete, F. Local permutations of products of Bell states and entanglement distillation. Phys. Rev. A 67, 022310 (2003).

    ADS  MATH  Google Scholar 

  50. Horodecki, M. & Horodecki, P. Reduction criterion of separability and limits for a class of distillation protocols. Phys. Rev. A 59, 4206–4216 (1999).

    ADS  MATH  Google Scholar 

  51. Alber, G., Delgado, A., Gisin, N. & Jex, I. Efficient bipartite quantum state purification in arbitrary dimensional Hilbert spaces. J. Phys. A 34, 8821–8833 (2001).

    ADS  MathSciNet  MATH  Google Scholar 

  52. Bombin, H. & Martin-Delgado, M. A. Entanglement distillation protocols and number theory. Phys. Rev. A 72, 032313 (2005).

    ADS  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

F.A.M. and V.G. acknowledge financial support by MUR (Ministero dell’Istruzione, dell’Università e della Ricerca) through the following projects: PNRR MUR project PE0000023-NQSTI, PRIN 2017 Taming complexity via Quantum Strategies: a Hybrid Integrated Photonic approach (QUSHIP) Id. 2017SRN-BRK, and project PRO3 Quantum Pathfinder. L.L. was partially supported by the Alexander von Humboldt Foundation. F.A.M. and L.L. thank the Freie Universität Berlin for hospitality. F.A.M., L.L. and V.G. thank D. Miller, M. Rosati, M. Notarnicola, M. Avesani, M. Mazelanik and M. Barbieri for useful discussions.

Author information

Authors and Affiliations

  1. NEST, Scuola Normale Superiore and Istituto Nanoscienze, Pisa, Italy

    Francesco Anna Mele

  2. QuSoft, Amsterdam, the Netherlands

    Ludovico Lami

  3. Korteweg-de Vries Institute for Mathematics, University of Amsterdam, Amsterdam, the Netherlands

    Ludovico Lami

  4. Institute for Theoretical Physics, University of Amsterdam, Amsterdam, the Netherlands

    Ludovico Lami

  5. Institut für Theoretische Physik und IQST, Universität Ulm, Ulm, Germany

    Ludovico Lami

  6. NEST, Scuola Normale Superiore and Istituto Nanoscienze, Consiglio Nazionale delle Ricerche, Pisa, Italy

    Vittorio Giovannetti

Authors
  1. Francesco Anna Mele
    View author publications

    Search author on:PubMed Google Scholar

  2. Ludovico Lami
    View author publications

    Search author on:PubMed Google Scholar

  3. Vittorio Giovannetti
    View author publications

    Search author on:PubMed Google Scholar

Contributions

The entanglement distribution protocol was designed and optimized by F.A.M. The proof of Theorem 1 was found in a blackboard discussion between the three authors. F.A.M. wrote a first complete draft of the paper, which was subsequently improved by L.L. and V.G.

Corresponding authors

Correspondence to Francesco Anna Mele, Ludovico Lami or Vittorio Giovannetti.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Photonics thanks Javier Fonollosa and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

36 pages of detailed derivations of our results.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mele, F.A., Lami, L. & Giovannetti, V. Maximum tolerable excess noise in continuous-variable quantum key distribution and improved lower bound on two-way capacities. Nat. Photon. 19, 329–334 (2025). https://doi.org/10.1038/s41566-024-01595-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41566-024-01595-9

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing