Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Boundary modes of a charge density wave state in a topological material

Nature Physics volume 20, pages 1253–1261 (2024)Cite this article

Subjects

Abstract

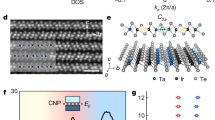
Charge density waves appear in numerous condensed matter platforms ranging from high-temperature superconductors to quantum Hall systems. Despite such ubiquity, there has been a lack of direct experimental study of boundary states that can uniquely stem from the charge order. Here we directly visualize the bulk and boundary phenomenology of the charge density wave in a topological material, Ta2Se8I, using scanning tunnelling microscopy. At a monolayer step edge, we demonstrate the presence of an in-gap boundary mode persisting up to the charge ordering temperature with modulations along the edge that match the charge density wave wavevector along the edge. Furthermore, these results manifesting the presence of an edge state challenge the existing axion insulator interpretation of the charge-ordered phase in this compound.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Electronic nature of charge density wave in Ta2Se8I.
Fig. 2: Observation of an edge state within the charge density wave gap.
Fig. 3: Temperature dependence of the charge density wave and its in-gap edge state.
Fig. 4: Correspondence between the periodicity of the edge dI/dV modulations and charge density wave wavelength projected along the edge.
Fig. 5: Gapless edge mode connecting the gapped bulk (and surface) conduction and valence bands in energy and phase.

Similar content being viewed by others

Data availability

All data needed to evaluate the conclusions in the paper are present in the paper. Additional data are available from the corresponding authors upon reasonable request. Source data are provided with this paper.

References

  1. Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).

    Article  ADS  Google Scholar 

  2. Yin, J. X., Pan, S. H. & Hasan, M. Z. Probing topological quantum matter with scanning tunneling microscopy. Nat. Rev. Phys. 3, 249–263 (2021).

    Article  Google Scholar 

  3. Hasan, M. Z. et al. Weyl, Dirac and high-fold chiral fermions in topological quantum matter. Nat. Rev. Mater. 6, 784–803 (2021).

    Article  ADS  Google Scholar 

  4. Nenno, D. M. et al. Axion physics in condensed-matter systems. Nat. Rev. Phys. 2, 682–696 (2020).

    Article  Google Scholar 

  5. Gooth, J. et al. Axionic charge-density wave in the Weyl semimetal (TaSe4)2I. Nature 575, 315–319 (2019).

    Article  ADS  Google Scholar 

  6. Allen, M. et al. Visualization of an axion insulating state at the transition between 2 chiral quantum anomalous Hall states. Proc. Natl Acad. Sci. USA 116, 14511–14515 (2019).

    Article  ADS  Google Scholar 

  7. Li, R., Wang, J., Qi, X.-L. & Zhang, S.-C. Dynamical axion field in topological magnetic insulators. Nat. Phys. 6, 284–288 (2010).

    Article  Google Scholar 

  8. Mogi, M. et al. A magnetic heterostructure of topological insulators as a candidate for an axion insulator. Nat. Mater. 16, 516–521 (2017).

    Article  ADS  Google Scholar 

  9. Liu, C. et al. Robust axion insulator and Chern insulator phases in a two-dimensional antiferromagnetic topological insulator. Nat. Mater. 19, 522–527 (2020).

    Article  ADS  Google Scholar 

  10. Zhang, D. et al. Topological axion states in magnetic insulator MnBi2Te4 with the quantized magnetoelectric effect. Phys. Rev. Lett. 122, 206401 (2019).

    Article  ADS  Google Scholar 

  11. Li, X.-P. et al. Type-III Weyl semimetals: (TaSe4)2I. Phys. Rev. B 103, L081402 (2021).

    Article  ADS  Google Scholar 

  12. Fijalkowski, K. M. et al. Any axion insulator must be a bulk three-dimensional topological insulator. Phys. Rev. B 103, 235111 (2021).

    Article  ADS  Google Scholar 

  13. Chiu, W.-C. et al. Causal structure of interacting Weyl fermions in condensed matter systems. Nat. Commun. 14, 2228 (2023).

    Article  ADS  Google Scholar 

  14. Shi, W. et al. A charge-density-wave topological semimetal. Nat. Phys. 17, 381–387 (2021).

    Article  Google Scholar 

  15. Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).

    Article  ADS  Google Scholar 

  16. Essin, A. M., Moore, J. E. & Vanderbilt, D. Magnetoelectric polarizability and axion electrodynamics in crystalline insulators. Phys. Rev. Lett. 102, 146805 (2009).

    Article  ADS  Google Scholar 

  17. Malashevich, A., Souza, I., Coh, S. & Vanderbilt, D. Theory of orbital magnetoelectric response. N. J. Phys. 12, 053032 (2010).

    Article  Google Scholar 

  18. Sinchenko, A. A., Ballou, R., Lorenzo, J. E., Grenet, T. H. & Monceau, P. Does (TaSe4)2I really harbor an axionic charge density wave? Appl. Phys. Lett. 120, 063102 (2022).

    Article  ADS  Google Scholar 

  19. Mitsuishi, N. et al. Switching of band inversion and topological surface states by charge density wave. Nat. Commun. 11, 2466 (2020).

    Article  ADS  Google Scholar 

  20. Yi, H. et al. Surface charge induced Dirac band splitting in a charge density wave material (TaSe4)2I. Phys. Rev. Res. 3, 013271 (2021).

    Article  Google Scholar 

  21. Huang, Z. et al. Absence of in-gap modes in charge density wave edge dislocations of the Weyl semimetal (TaSe4)2I. Phys. Rev. B 104, 205138 (2021).

    Article  ADS  Google Scholar 

  22. Aketagawa, M. & Takada, K. Correction of distorted STM image by using a regular crystalline lattice and 2D FFT. Nanotechnology 6, 105 (1995).

    Article  ADS  Google Scholar 

  23. Lee, K. B., Davidov, D. & Heeger, A. J. X-ray-diffraction study of the CDW phase in (TaSe4)2I-determination of the CDW modulation amplitude. Solid State Commun. 54, 673–677 (1985).

    Article  ADS  Google Scholar 

  24. Requardt, H., Kalning, M., Burandt, B., Press, W. & Currat, R. Critical x-ray scattering at the Peierls transition in the quasi-one-dimensional system (TaSe4)2I. J. Phys. Condens. Matter 8, 2327 (1996).

    Article  ADS  Google Scholar 

  25. Smaalen, S., Lam, E. J. & Ludecke, J. Structure of the charge-density-wave in (TaSe4)2I. J. Phys. Condens. Matter 13, 9923 (2001).

    Article  ADS  Google Scholar 

  26. Fujishita, H., Sato, M. & Hoshino, S. Incommensurate superlattice reflections in quasi-one-dimensional conductors, (TaSe4)2I and (NbSe4)2I. Solid State Commun. 49, 313–316 (1984).

    Article  ADS  Google Scholar 

  27. Favre-Nicolin, V. et al. Structural evidence for Ta-tetramerization displacements in the charge density-wave compound (TaSe4)2I from x-ray anomalous diffraction. Phys. Rev. Lett. 87, 015502 (2001).

    Article  ADS  Google Scholar 

  28. Fujishita, H., Shapiro, S. M., Sato, M. & Hoshino, S. A neutron-scattering study of the quasi-one-dimensional conductor (TaSe4)2I. J. Phys. C: Solid State Phys. 19, 3049 (1986).

    Article  ADS  Google Scholar 

  29. Lorenzo, J. E. et al. A neutron scattering study of the quasi-one-dimensional conductor (TaSe4)2I. J. Phys. Condens. Matter 10, 5039–5068 (1998).

    Article  ADS  Google Scholar 

  30. Li, G. et al. Chirality locking charge density waves in a chiral crystal. Nat. Commun. 13, 2914 (2022).

    Article  ADS  Google Scholar 

  31. Stoltz, D. et al. Tunneling evidence for spatial location of the charge-density-wave induced band splitting in 1T-TaSe2. Phys. Rev. B 76, 073410 (2007).

    Article  ADS  Google Scholar 

  32. Mallet, P. et al. Contrast reversal of the charge density wave STM image in purple potassium molybdenum bronze K0.9Mo6O17. Phys. Rev. B 60, 2122 (1999).

    Article  ADS  Google Scholar 

  33. Tournier-Colletta, C. et al. Electronic instability in a zero-gap semiconductor: the charge density wave in (TaSe4)2I. Phys. Rev. Lett. 110, 236401 (2013).

    Article  ADS  Google Scholar 

  34. Grüner, G. The dynamics of charge-density waves. Rev. Mod. Phys. 60, 1129 (1988).

    Article  ADS  Google Scholar 

  35. Flicker, F. & van Wezel, J. Charge order from orbital-dependent coupling evidenced by NbSe2. Nat. Commun. 6, 7034 (2015).

    Article  ADS  Google Scholar 

  36. Varma, C. M. & Simons, A. L. Strong-coupling theory of charge-density-wave transitions. Phys. Rev. Lett. 51, 138 (1983).

    Article  ADS  Google Scholar 

  37. Zhang, Y. et al. First-principles study of the low-temperature charge density wave phase in the quasi-one-dimensional Weyl chiral compound (TaSe4)2I. Phys. Rev. B 101, 174106 (2020).

    Article  ADS  Google Scholar 

  38. Wang, Z. et al. Electronic nature of chiral charge order in the kagome superconductor CsV3Sb5. Phys. Rev. B 104, 075148 (2021).

    Article  ADS  Google Scholar 

  39. Stühler, R. et al. Tomonaga–Luttinger liquid in the edge channels of a quantum spin Hall insulator. Nat. Phys. 16, 47–51 (2020).

    Article  Google Scholar 

  40. Kane, C. L. & Mele, E. J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).

    Article  ADS  Google Scholar 

  41. Bernevig, B. A. & Zhang, S.-C. Quantum spin Hall effect. Phys. Rev. Lett. 96, 106802 (2006).

    Article  ADS  Google Scholar 

  42. Bernevig, B. A., Hughes, T. L. & Zhang, S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006).

    Article  ADS  Google Scholar 

  43. König, M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007).

    Article  ADS  Google Scholar 

  44. Yin, J. X. et al. Quantum-limit Chern topological magnetism in TbMn6Sn6. Nature 583, 533–536 (2020).

    Article  ADS  Google Scholar 

  45. Shumiya, N. et al. Evidence of a room-temperature quantum spin Hall edge state in a higher-order topological insulator. Nat. Mater. 21, 1111–1115 (2022).

    Article  ADS  Google Scholar 

  46. Drozdov, I. K. et al. One-dimensional topological edge states of bismuth bilayers. Nat. Phys. 10, 664–669 (2014).

    Article  Google Scholar 

  47. Tang, S. et al. Quantum spin Hall state in monolayer 1T′-WTe2. Nat. Phys. 13, 683–687 (2017).

    Article  Google Scholar 

  48. Wu, R. et al. Evidence for topological edge states in a large energy gap near the step edges on the surface of ZrTe5. Phys. Rev. X 6, 021017 (2016).

    Google Scholar 

  49. Li, X.-B. et al. Experimental observation of topological edge states at the surface step edge of the topological insulator ZrTe5. Phys. Rev. Lett. 116, 176803 (2016).

    Article  ADS  Google Scholar 

  50. Wang, Z. et al. Topological edge states in a high-temperature superconductor FeSe/SrTiO3(001) film. Nat. Mater. 15, 968–973 (2016).

    Article  ADS  Google Scholar 

  51. Sessi, P. et al. Robust spin-polarized midgap states at step edges of topological crystalline insulators. Science 354, 1269–1273 (2016).

    Article  ADS  MathSciNet  Google Scholar 

  52. Peng, L. et al. Observation of topological states residing at step edges of WTe2. Nat. Commun. 8, 659 (2017).

    Article  ADS  Google Scholar 

  53. Liu, S. et al. Experimental observation of conductive edge states in weak topological insulator candidate HfTe5. APL Mater. 6, 121111 (2018).

    Article  ADS  Google Scholar 

  54. Ugeda, M. M. et al. Observation of topologically protected states at crystalline phase boundaries in single-layer WSe2. Nat. Commun. 9, 3401 (2018).

    Article  ADS  Google Scholar 

  55. Reis, F. et al. Bismuthene on a SiC substrate: a candidate for a high-temperature quantum spin Hall material. Science 357, 287–290 (2017).

    Article  ADS  MathSciNet  Google Scholar 

  56. Zhang, X. et al. Eightfold fermionic excitation in a charge density wave compound. Phys. Rev. B 102, 035125 (2020).

    Article  ADS  Google Scholar 

  57. Wieder, B. J., Lin, K.-S. & Bradlyn, B. Axionic band topology in inversion-symmetric Weyl-charge-density waves. Phys. Rev. Res. 2, 042010(R) (2020).

    Article  Google Scholar 

  58. Zhang, S.-B. et al. Emergent edge modes in shifted quasi-one-dimensional charge density waves. Phys. Rev. Lett. 130, 106203 (2023).

    Article  ADS  Google Scholar 

  59. Chang, G. et al. Topological quantum properties of chiral crystals. Nat. Mater. 17, 978–985 (2018).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

The M.Z.H. group acknowledges primary support from the US Department of Energy, Office of Science, National Quantum Information Science Research Centers, Quantum Science Center (at ORNL) and Princeton University; scanning tunneling microscopy instrumentation support from the Gordon and Betty Moore Foundation (GBMF9461) and the theory work; and support from the US DOE under the Basic Energy Sciences programme (grant number DOE/BES DE-FG-02-05ER46200) for the theory and sample characterization work including photoemission spectroscopy. T.N. acknowledges supports from the European Union’s Horizon 2020 research and innovation programme (ERC-StG-Neupert-757867-PARATOP) and from the Swiss National Science Foundation through a Consolidator Grant (iTQC, TMCG-2_213805). Work at Nanyang Technological University was supported by the National Research Foundation, Singapore, under its Fellowship Award (NRF-NRFF13-2021-0010), the Agency for Science, Technology and Research (A*STAR) under its Manufacturing, Trade and Connectivity (MTC) Individual Research Grant (IRG) (Grant No.: M23M6c0100), and the Nanyang Assistant Professorship grant (NTU-SUG). Crystal growth at Beijing Institute of Technology is supported by National Science Foundation of China (NSFC) (grant nos 92065109, 12321004 and 12234003), the National Key R&D Program of China (grant nos 2020YFA0308800 and 2022YFA1403400) and the Beijing Natural Science Foundation (grant no. Z210006). Z.W. thanks the Analysis and Testing Center at BIT for assistance through facility support. S.-B.Z. is supported by the Innovation Program for Quantum Science and Technology (grant no. 2021ZD0302800) and the Anhui Initiative in Quantum Information Technologies (grant no. AHY170000). Crystal growth at Max Planck Institute for Chemical Physics of Solids is funded by European Research Council (ERC) advanced grant no. 742068 (‘TOPMAT’), the Deutsche Forschungsgemeinschaft (DFG) under SFB 1143 (project no. 247310070) and the Würzburg-Dresden Cluster of Excellence on Complexity and Topology in Quantum Matter – ct.qmat (EXC 2147, project no. 39085490). G. Cheng and N.Y. acknowledge the use of Princeton’s Imaging and Analysis Center, which is partially supported by the Princeton Center for Complex Materials, a National Science Foundation (NSF)-MRSEC programme (DMR-2011750). X.L. acknowledges support from the National Key R&D Program of China (grant no. 2022YFA1403700).

Author information

Author notes

  1. These authors contributed equally: Maksim Litskevich, Md Shafayat Hossain, Song-Bo Zhang.

Authors and Affiliations

  1. Laboratory for Topological Quantum Matter and Advanced Spectroscopy (B7), Department of Physics, Princeton University, Princeton, NJ, USA

    Maksim Litskevich, Md Shafayat Hossain, Zi-Jia Cheng, Jia-Xin Yin, Qi Zhang, Tyler A. Cochran, Nana Shumiya, Yu-Xiao Jiang, Xian P. Yang, Daniel Multer & M. Zahid Hasan

  2. Hefei National Laboratory, Hefei, China

    Song-Bo Zhang

  3. International Center for Quantum Design of Functional Materials, University of Science and Technology of China, Hefei, China

    Song-Bo Zhang

  4. Department of Physics, University of Zurich, Zurich, Switzerland

    Song-Bo Zhang, Xiaoxiong Liu & Titus Neupert

  5. Max Planck Institute for Chemical Physics of Solids, Dresden, Germany

    Satya N. Guin, Nitesh Kumar, Chandra Shekhar & Claudia Felser

  6. Department of Chemistry, Birla Institute of Technology and Science, Hyderabad, India

    Satya N. Guin

  7. S. N. Bose National Centre for Basic Sciences, Salt Lake City, India

    Nitesh Kumar

  8. Centre for Quantum Physics, Key Laboratory of Advanced Optoelectronic Quantum Architecture and Measurement (MOE), School of Physics, Beijing Institute of Technology, Beijing, China

    Zhiwei Wang, Yongkai Li & Yugui Yao

  9. Beijing Key Lab of Nanophotonics and Ultrafine Optoelectronic Systems, Beijing Institute of Technology, Beijing, China

    Zhiwei Wang, Yongkai Li & Yugui Yao

  10. Material Science Center, Yangtze Delta Region Academy of Beijing Institute of Technology, Jiaxing, China

    Zhiwei Wang & Yongkai Li

  11. Division of Physics and Applied Physics, School of Physical and Mathematical Sciences, Nanyang Technological University, Singapore, Singapore

    Guoqing Chang

  12. Princeton Materials Institute, Princeton University, Princeton, NJ, USA

    Guangming Cheng & Nan Yao

  13. Shenzhen Institute for Quantum Science and Engineering and Department of Physics, Southern University of Science and Technology, Shenzhen, China

    Xiaoxiong Liu

  14. Quantum Science Center of Guangdong-Hong Kong-Macao Greater Bay Area (Guangdong), Shenzhen, China

    Xiaoxiong Liu

  15. Shenzhen Key Laboratory of Quantum Science and Engineering, Shenzhen, China

    Xiaoxiong Liu

  16. International Quantum Academy, Shenzhen, China

    Xiaoxiong Liu

  17. Quantum Science Center (QSC, ORNL), Oak Ridge, TN, USA

    M. Zahid Hasan

Authors
  1. Maksim Litskevich
    View author publications

    Search author on:PubMed Google Scholar

  2. Md Shafayat Hossain
    View author publications

    Search author on:PubMed Google Scholar

  3. Song-Bo Zhang
    View author publications

    Search author on:PubMed Google Scholar

  4. Zi-Jia Cheng
    View author publications

    Search author on:PubMed Google Scholar

  5. Satya N. Guin
    View author publications

    Search author on:PubMed Google Scholar

  6. Nitesh Kumar
    View author publications

    Search author on:PubMed Google Scholar

  7. Chandra Shekhar
    View author publications

    Search author on:PubMed Google Scholar

  8. Zhiwei Wang
    View author publications

    Search author on:PubMed Google Scholar

  9. Yongkai Li
    View author publications

    Search author on:PubMed Google Scholar

  10. Guoqing Chang
    View author publications

    Search author on:PubMed Google Scholar

  11. Jia-Xin Yin
    View author publications

    Search author on:PubMed Google Scholar

  12. Qi Zhang
    View author publications

    Search author on:PubMed Google Scholar

  13. Guangming Cheng
    View author publications

    Search author on:PubMed Google Scholar

  14. Tyler A. Cochran
    View author publications

    Search author on:PubMed Google Scholar

  15. Nana Shumiya
    View author publications

    Search author on:PubMed Google Scholar

  16. Yu-Xiao Jiang
    View author publications

    Search author on:PubMed Google Scholar

  17. Xian P. Yang
    View author publications

    Search author on:PubMed Google Scholar

  18. Daniel Multer
    View author publications

    Search author on:PubMed Google Scholar

  19. Xiaoxiong Liu
    View author publications

    Search author on:PubMed Google Scholar

  20. Nan Yao
    View author publications

    Search author on:PubMed Google Scholar

  21. Yugui Yao
    View author publications

    Search author on:PubMed Google Scholar

  22. Claudia Felser
    View author publications

    Search author on:PubMed Google Scholar

  23. Titus Neupert
    View author publications

    Search author on:PubMed Google Scholar

  24. M. Zahid Hasan
    View author publications

    Search author on:PubMed Google Scholar

Contributions

STM experiments were performed by M.L. and M.S.H. in consultation with M.Z.H. Crystal growth was carried out by S.N.G., N.K., C.S., Z.W. and Y.L under supervision of Y.Y. and C.F. Transmission electron microscopy measurements were performed by G.C. and N.Y. ARPES experiments were performed by Z.-J.C. in consultation with M.S.H. and M.Z.H. Theoretical modelling and calculations uncovering the underlying topology of the boundary mode were carried out by S.-B.Z. and X.L. under supervision of T.N. Writing of the manuscript and figure production were undertaken by M.S.H., M.L., S.-B.Z., T.N., Z.-J.C. and M.Z.H. All the authors contributed to the discussion of the results, interpretation and conclusion.

Corresponding authors

Correspondence to Md Shafayat Hossain or M. Zahid Hasan.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Amit Agarwal, Somesh Ganguli and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary discussion and Figs. 1–14.

Source data

Source Data Fig. 1

Source data with the Excel sheet names indicating the corresponding figure panel.

Source Data Fig. 2

Source data with the Excel sheet names indicating the corresponding figure panel.

Source Data Fig. 3

Source data with the Excel sheet names indicating the corresponding figure panel.

Source Data Fig. 4

Source data with the Excel sheet names indicating the corresponding figure panel.

Source Data Fig. 5

Source data with the Excel sheet names indicating the corresponding figure panel.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Litskevich, M., Hossain, M.S., Zhang, SB. et al. Boundary modes of a charge density wave state in a topological material. Nat. Phys. 20, 1253–1261 (2024). https://doi.org/10.1038/s41567-024-02469-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-024-02469-1

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing