Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Directed percolation and puff jamming near the transition to pipe turbulence

Nature Physics volume 20, pages 1339–1345 (2024)Cite this article

Subjects

Abstract

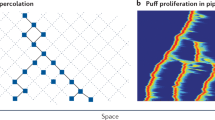
The onset of turbulence in pipe flow has defied detailed understanding ever since the first observations of the spatially heterogeneous nature of the transition. Recent theoretical studies and experiments in simpler, shear-driven flows suggest that the onset of turbulence is a directed-percolation non-equilibrium phase transition, but whether these findings are generic and also apply to open or pressure-driven flows is unknown. In pipe flow, the extremely long time scales near the transition make direct observations of critical behaviour virtually impossible. Here we find a technical solution to that limitation and show that the universality class of the transition is directed percolation, from which a jammed phase of puffs emerges above the critical point. Our method is to experimentally characterize all pairwise interactions between localized patches of turbulence puffs and use these interactions as input for renormalization group and computer simulations of minimal models that extrapolate to long length and time scales. The strong interactions in the jamming regime enable us to explicitly measure the turbulent fraction and confirm model predictions. Our work shows that directed-percolation scaling applies beyond simple closed shear flows and underscores how statistical mechanics can lead to profound, quantitative and predictive insights on turbulent flows and their phases.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Illustration of the bottom-up multiscale approach to the laminar–turbulent transition in pipe flow used in this study.
Fig. 2: Puff dynamics as a function of puff-to-puff separation and Re.
Fig. 3: Scaling relationships obtained by simulating equation (3) using the experimentally obtained puff interactions.
Fig. 4: Puff jamming in pipe flow represented by a local Lindemann criterion.
Fig. 5: Puff density as a function of the rates at which puffs split (1/τs) and decay (1/τd).

Similar content being viewed by others

Data availability

All experimental data presented in this article are available online in the Zenodo repository at https://doi.org/10.5281/zenodo.10308791 (ref. 37).

Code availability

All computational data presented in this paper, the codes used to generate and process those data and the codes and scripts used to generate the figures are available online in the Zenodo repository at https://doi.org/10.5281/zenodo.10308791 (ref. 37).

References

  1. Reynolds, O. An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous and the law of resistance in parallel channel. Philos. Trans. R. Soc. Lond. 174, 935 (1883).

    ADS  Google Scholar 

  2. Rotta, J. Experimenteller beitrag zur entstehung turbulenter strömung im rohr. Ing.-Arch. 24, 258–281 (1956).

    Article  Google Scholar 

  3. Wygnanski, I. J. & Champagne, F. On transition in a pipe. Part 1. The origin of puffs and slugs and the flow in a turbulent slug. J. Fluid Mech. 59, 281–335 (1973).

    Article  ADS  Google Scholar 

  4. Shimizu, M. & Kida, S. A driving mechanism of a turbulent puff in pipe flow. Fluid Dyn. Res. 41, 045501 (2009).

    Article  ADS  Google Scholar 

  5. Tuckerman, L. S., Chantry, M. & Barkley, D. Patterns in wall-bounded shear flows. Annu. Rev. Fluid Mech. 52, 343–367 (2020).

    Article  ADS  MathSciNet  Google Scholar 

  6. Avila, M., Barkley, D. & Hof, B. Transition to turbulence in pipe flow. Annu. Rev. Fluid Mech. 55, 575–602 (2023).

    Article  ADS  Google Scholar 

  7. Song, B. & Hof, B. Deterministic and stochastic aspects of the transition to turbulence. J. Stat. Mech. Theory Exp. 2014, P02001 (2014).

    Article  Google Scholar 

  8. Manneville, P. On the transition to turbulence of wall-bounded flows in general, and plane Couette flow in particular. Eur. J. Mech. B Fluids 49, 345–362 (2015).

    Article  MathSciNet  Google Scholar 

  9. Barkley, D. Theoretical perspective on the route to turbulence in a pipe. J. Fluid Mech. 803, P1 (2016).

    Article  ADS  MathSciNet  Google Scholar 

  10. Pomeau, Y. The long and winding road. Nat. Phys. 12, 198–199 (2016).

    Article  Google Scholar 

  11. Goldenfeld, N. & Shih, H.-Y. Turbulence as a problem in non-equilibrium statistical mechanics. J. Stat. Phys. 167, 575–594 (2017).

    Article  ADS  MathSciNet  Google Scholar 

  12. Avila, K. et al. The onset of turbulence in pipe flow. Science 333, 192–196 (2011).

    Article  ADS  Google Scholar 

  13. Pomeau, Y. Front motion, metastability and subcritical bifurcations in hydrodynamics. Physica D 23, 3–11 (1986).

    Article  ADS  Google Scholar 

  14. Chaté, H. & Manneville, P. Transition to turbulence via spatio-temporal intermittency. Phys. Rev. Lett. 58, 112 (1987).

    Article  ADS  Google Scholar 

  15. Moxey, D. & Barkley, D. Distinct large-scale turbulent-laminar states in transitional pipe flow. Proc. Natl Acad. Sci. USA 107, 8091–8096 (2010).

    Article  ADS  Google Scholar 

  16. Sipos, M. & Goldenfeld, N. Directed percolation describes lifetime and growth of turbulent puffs and slugs. Phys. Rev. E 84, 035304 (2011).

    Article  ADS  Google Scholar 

  17. Barkley, D. Simplifying the complexity of pipe flow. Phys. Rev. E 84, 016309 (2011).

    Article  ADS  Google Scholar 

  18. Shi, L., Avila, M. & Hof, B. Scale invariance at the onset of turbulence in Couette flow. Phys. Rev. Lett. 110, 204502 (2013).

    Article  ADS  Google Scholar 

  19. Shih, H.-Y., Hsieh, T.-L. & Goldenfeld, N. Ecological collapse and the emergence of travelling waves at the onset of shear turbulence. Nat. Phys. 12, 245 (2016).

    Article  Google Scholar 

  20. Chantry, M., Tuckerman, L. S. & Barkley, D. Universal continuous transition to turbulence in a planar shear flow. J. Fluid Mech. 824, R1 (2017).

    Article  ADS  MathSciNet  Google Scholar 

  21. Lemoult, G. et al. Directed percolation phase transition to sustained turbulence in couette flow. Nat. Phys. 12, 254–258 (2016).

    Article  Google Scholar 

  22. Klotz, L., Lemoult, G., Avila, K. & Hof, B. Phase transition to turbulence in spatially extended shear flows. Phys. Rev. Lett. 128, 014502 (2022).

    Article  ADS  Google Scholar 

  23. Goldenfeld, N. Lectures on Phase Transitions and the Renormalization Group (Addison-Wesley, 1992).

  24. Dauchot, O. & Bertin, E. Subcritical transition to turbulence: what we can learn from the physics of glasses. Phys. Rev. E 86, 036312 (2012).

    Article  ADS  Google Scholar 

  25. Hof, B., De Lozar, A., Avila, M., Tu, X. & Schneider, T. M. Eliminating turbulence in spatially intermittent flows. Science 327, 1491–1494 (2010).

    Article  ADS  Google Scholar 

  26. Mukund, V. & Hof, B. The critical point of the transition to turbulence in pipe flow. J. Fluid Mech. 839, 76–94 (2018).

    Article  ADS  MathSciNet  Google Scholar 

  27. Barkley, D. et al. The rise of fully turbulent flow. Nature 526, 550 (2015).

    Article  ADS  Google Scholar 

  28. Kreilos, T. et al. Bypass transition and spot nucleation in boundary layers. Phys. Rev. Fluids 1, 043602 (2016).

    Article  ADS  Google Scholar 

  29. Wang, X., Shih, H.-Y. & Goldenfeld, N. Stochastic model for quasi-one-dimensional transitional turbulence with streamwise shear interactions. Phys. Rev. Lett. 129, 034501 (2022).

    Article  ADS  Google Scholar 

  30. Hinrichsen, H. Non-equilibrium critical phenomena and phase transitions into absorbing states. Adv. Phys. 49, 815–958 (2000).

    Article  ADS  Google Scholar 

  31. Helbing, D. Traffic and related self-driven many-particle systems. Rev. Mod. Phys. 73, 1067 (2001).

    Article  ADS  MathSciNet  Google Scholar 

  32. Klumpp, S. & Hwa, T. Stochasticity and traffic jams in the transcription of ribosomal RNA: Intriguing role of termination and antitermination. Proc. Natl Acad. Sci. USA 105, 18159–18164 (2008).

    Article  ADS  Google Scholar 

  33. Kim, S. & Jacobs-Wagner, C. Effects of mRNA degradation and site-specific transcriptional pausing on protein expression noise. Biophys. J. 114, 1718–1729 (2018).

    Article  ADS  Google Scholar 

  34. Chatterjee, P., Goldenfeld, N. & Kim, S. DNA supercoiling drives a transition between collective modes of gene synthesis. Phys. Rev. Lett. 127, 218101 (2021).

    Article  ADS  Google Scholar 

  35. Lighthill, M. J. & Whitham, G. B. On kinematic waves II. A theory of traffic flow on long crowded roads. Proc. R. Soc. Lond. A 229, 317–345 (1955).

    Article  ADS  MathSciNet  Google Scholar 

  36. Jensen, I. Low-density series expansions for directed percolation on square and triangular lattices. J. Phys. A 29, 7013–7040 (1996).

    Article  ADS  MathSciNet  Google Scholar 

  37. Lemoult, G. Directed percolation and puff jamming near the transition to pipe turbulence. Zenodo https://doi.org/10.5281/zenodo.10308791 (2024).

Download references

Acknowledgements

We gratefully acknowledge the assistance of J. M. Lopez with DNSs at an early stage of this work. This work was partially supported by two grants from the Simons Foundation (grant nos. 662985 (N.G.) and 662960 (B.H.)) and by Ministry of Science and Technology, Taiwan (grant nos. MOST 109-2112-M-001-017-MY3 and MOST 111-2112-M-001-027-MY3 (H.-Y.S.)). Part of this work was performed using computing resources of CRIANN (Normandy, France).

Author information

Authors and Affiliations

  1. LOMC, CNRS UMR 6294, Université Le Havre Normandie, Le Havre, France

    Grégoire Lemoult

  2. Institute of Science and Technology Austria, Klosterneuburg, Austria

    Grégoire Lemoult, Vasudevan Mukund & Björn Hof

  3. Department of Physics, University of Illinois at Urbana-Champaign, Loomis Laboratory of Physics, Urbana, IL, USA

    Hong-Yan Shih & Nigel Goldenfeld

  4. Institute of Physics, Academia Sinica, Taipei, Taiwan

    Hong-Yan Shih

  5. Physics Division, National Center for Theoretical Sciences, Taipei, Taiwan

    Hong-Yan Shih

  6. Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark

    Gaute Linga & Joachim Mathiesen

  7. PoreLab, The Njord Centre, Departments of Physics and Geosciences, University of Oslo, Oslo, Norway

    Gaute Linga

  8. Department of Physics, University of California San Diego, La Jolla, CA, USA

    Nigel Goldenfeld

Authors
  1. Grégoire Lemoult
    View author publications

    Search author on:PubMed Google Scholar

  2. Vasudevan Mukund
    View author publications

    Search author on:PubMed Google Scholar

  3. Hong-Yan Shih
    View author publications

    Search author on:PubMed Google Scholar

  4. Gaute Linga
    View author publications

    Search author on:PubMed Google Scholar

  5. Joachim Mathiesen
    View author publications

    Search author on:PubMed Google Scholar

  6. Nigel Goldenfeld
    View author publications

    Search author on:PubMed Google Scholar

  7. Björn Hof
    View author publications

    Search author on:PubMed Google Scholar

Contributions

B.H., N.G. and J.M. designed the project. B.H., G. Lemoult and V.M. performed experiments and computer simulations. H.-Y.S., G. Linga, J.M. and N.G. performed theoretical calculations and computer simulations. All authors contributed to the interpretation of the data and the writing of the paper.

Corresponding authors

Correspondence to Nigel Goldenfeld or Björn Hof.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Ron Shnapp and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Information containing details of the experiments as well as theoretical and numerical calculations of models of puff interactions near the laminar–turbulent transition in pipe flow, and Supplementary Figs. 1–14 and Tables 1–3.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lemoult, G., Mukund, V., Shih, HY. et al. Directed percolation and puff jamming near the transition to pipe turbulence. Nat. Phys. 20, 1339–1345 (2024). https://doi.org/10.1038/s41567-024-02513-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-024-02513-0

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing