Abstract
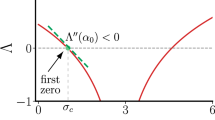
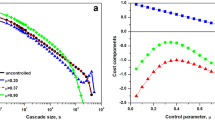
In complex systems, external parameters often determine the phase in which the system operates, that is, its macroscopic behaviour. For nearly a century, statistical physics has been used to extensively study systems’ transitions across phases, (universal) critical exponents and related dynamical properties. Here we consider the functionality of systems, particularly operations in socio-technical ones, production in economic ones and, more generally, any schedule-based system, where timing is of crucial importance. We introduce a stylized model of delay propagation on temporal networks, where the magnitude of the delay-mitigating buffer acts as a control parameter. The model exhibits timeliness criticality, a novel form of critical behaviour. We characterize fluctuations near criticality, commonly referred to as avalanches, and identify the corresponding critical exponents. The model exhibits timeliness criticality also when run on real-world temporal systems such as production networks. Additionally, we explore potential connections with the mode-coupling theory of glasses, depinning transition and directed polymer problem.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The source data for all figures in the paper (including Supplementary Figs. 1–6) are linked from the ‘Data and codes for figures’ section in the Supplementary Information to the respective folders in the GitHub repository (https://github.com/jose-moran/timeliness_criticality/tree/main/figures/).
Code availability
The codes used to generate all the figures in the paper (including Supplementary Figs. 1–6) are linked from the ‘Data and codes for figures’ section in the Supplementary Information to the respective folders in the GitHub repository (https://github.com/jose-moran/timeliness_criticality/tree/main/figures/).
References
Moran, J., Pijpers, F. P., Weitzel, U., Bouchaud, J.-P. & Panja, D. Temporal criticality in socio-technical systems. Preprint at https://arxiv.org/abs/2307.03546 (2023).
Dekker, M. M. & Panja, D. Cascading dominates large-scale disruptions in transport over complex networks. PLoS ONE 16, e0246077 (2021).
Giannikas, V. et al. A data-driven method to assess the causes and impact of delay propagation in air transportation systems. Transp. Res. Part C: Emerg. Technol. 143, 103862 (2022).
Ledwoch, A., Brintrup, A., Mehnen, J. örn & Tiwari, A. Systemic risk assessment in complex supply networks. IEEE Syst. J. 12, 1826–1837 (2016).
Brintrup, A. & Ledwoch, A. Supply network science: emergence of a new perspective on a classical field. Chaos 28, 033120 (2018).
Colon, C. élian & Ghil, M. Economic networks: heterogeneity-induced vulnerability and loss of synchronization. Chaos 27, 126703 (2017).
The Associated Press. Ship still stuck in Suez Canal as backlog grows to 150 other ships. CBC (25 March 2021).
Colon, C., Hallegatte, S. & Rozenberg, J. Criticality analysis of a country’s transport network via an agent-based supply chain model. Nat. Sustain. 4, 209–215 (2020).
Kosasih, E. E. & Brintrup, A. Reinforcement learning provides a flexible approach for realistic supply chain safety stock optimisation. IFAC-PapersOnLine 55, 1539–1544 (2022).
Dessertaine, T., Moran, J., Benzaquen, M. & Bouchaud, J.-P. Out-of-equilibrium dynamics and excess volatility in firm networks. J. Econ. Dyn. Control 138, 104362 (2022).
Munoz, M. A. & Hwa, T. On nonlinear diffusion with multiplicative noise. Europhys. Lett. 41, 147 (1998).
Hinrichsen, H. Non-equilibrium critical phenomena and phase transitions into absorbing states. Adv. Phys. 49, 815–958 (2000).
Götze, W. Complex Dynamics of Glass-Forming Liquids: A Mode-Coupling Theory Vol. 143 (Oxford Univ. Press, 2009).
Holme, P. & Saramäki, J. Temporal networks. Phys. Rep. 519., 97–125 (2012).
Holme, P. and Saramäki, J. Temporal Networks (SpringerLink, 2013).
Sellitto, M., Biroli, G. & Toninelli, C. Facilitated spin models on Bethe lattice: bootstrap percolation, mode-coupling transition and glassy dynamics. Europhys. Lett. 69, 496 (2005).
Rosso, A., Le Doussal, P. & Wiese, K. J. Avalanche-size distribution at the depinning transition: a numerical test of the theory. Phys. Rev. B 80, 144204 (2009).
Bouchaud, E. Scaling properties of cracks. J. Phys.: Condens. Matter 9, 4319 (1997).
Lin, J., Lerner, E., Rosso, A. & Wyart, M. Scaling description of the yielding transition in soft amorphous solids at zero temperature. Proc. Natl Acad. Sci. USA 111, 14382–14387 (2014).
Ponson, L. & Pindra, N. Crack propagation through disordered materials as a depinning transition: a critical test of the theory. Phys. Rev. E 95, 053004 (2017).
Newman, M. E. J. & Barkema, G. T. Monte Carlo Methods in Statistical Physics (Oxford Univ. Press, 1999).
Mastrandrea, R., Fournet, J. & Barrat, A. Contact patterns in a high school: a comparison between data collected using wearable sensors, contact diaries and friendship surveys. PLoS ONE 10, e0136497 (2015).
Génois, M. et al. Data on face-to-face contacts in an office building suggest a low-cost vaccination strategy based on community linkers. Network Sci. 3, 326–347 (2015).
Dekker, M. M., Schram, R. D., Ou, J. & Panja, D. Hidden dependence of spreading vulnerability on topological complexity. Phys. Rev. E 105, 054301 (2022).
Dekker, M. M. et al. Quantifying agent impacts on contact sequences in social interactions. Sci. Rep. 12, 3483 (2022).
Roux, S. & Herrmann, H. J. Disorder induced nonlinear conductivity. Europhys. Lett. 4, 1227 (1987).
Wichmann, P., Brintrup, A., Baker, S., Woodall, P. & McFarlane, D. Towards automatically generating supply chain maps from natural language text. IFAC-PapersOnLine 51, 1726–1731 (2018).
Sterman, J. Modeling managerial behavior: misperceptions of feedback in a dynamic decision making experiment. Manage. Sci. 35, 321–339 (1989).
Dekker, M. M. et al. A next step in disruption management: combining operations research and complexity science. Public Transp. 14, 5–26 (2021).
Shughrue, C., Werner, B. & Seto, K. C. Global spread of local cyclone damages through urban trade networks. Nat. Sustain. 3, 606–613 (2020).
Bak, P., Chen, K., Scheinkman, J. & Woodford, M. Aggregate fluctuations from independent sectoral shocks: self-organized criticality in a model of production and inventory dynamics. Ric. Econ. 47, 3–30 (1993).
Moran, J. & Bouchaud, J.-P. May’s instability in large economies. Phys. Rev. E 100, 032307 (2019).
Bernanke, B. S., Gertler, M. & Gilchrist, S. The financial accelerator and the flight to quality. Rev. Econ. Stat. 78, 1–15 (1996).
Bernanke, B. S., Geithner, T. F. & Paulson Jr, H. M. Firefighting: The Financial Crisis and Its Lessons (Penguin, 2019).
Gabaix, X. The granular origins of aggregate fluctuations. Econometrica 79, 733–772 (2011).
Carvalho, V. M. & Tahbaz, A. Production networks: a primer. Annu. Rev. Econ. 11, 635–663 (2019).
Pichler, A. & Farmer, J. D. Simultaneous supply and demand constraints in input–output networks: the case of COVID-19 in Germany, Italy, and Spain. Econ. Syst. Res. 34, 273–293 (2021).
Lafrogne-Joussier, R., Martin, J. & Mejean, I. Supply shocks in supply chains: evidence from the early lockdown in China. IMF Econ. Rev. 71, 170–215 (2022).
Pichler, A. & Diem, C. et al. Building an alliance to map global supply networks. Science 382, 270–272 (2023).
Author information
Authors and Affiliations
Contributions
J.-P.B. and D.P. conceptualized the timeliness criticality. J.-P.B., P.L.D., J.M., D.P., F.P.P. and M.R. analysed the timeliness criticality. All authors contributed to the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Yuichi Ikeda and Jari Saramäki for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 An example of how an avalanche is defined.
The mean delay per node for the mean-field case is plotted (blue), along with an orange line corresponding to mean delay equals B (see text for the parameter values used for this plot). For the avalanche shown, we define tstart = 4, 760, 908 as the time when the mean delay per node exceeds B, and tend = 4, 785, 490 as the time when for the first time after tstart the mean delay per node falls below B again. Then the mean delay per node in the interval \(\left[{t}_{{{{\rm{start}}}}},{t}_{{{{\rm{end}}}}}\right)\) constitutes a delay avalanche, from which the persistence time and the size of the avalanche are obtained respectively as tp = tend − tstart = 24, 582, and as the area between the blue curve and the orange line over the interval \(\left[{t}_{{{{\rm{start}}}}},{t}_{{{{\rm{end}}}}}\right)\).
Supplementary information
Supplementary Information
Supplementary Sections A–E, Figs. 1–6 and Tables 1 and 2.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Moran, J., Romeijnders, M., Doussal, P.L. et al. Timeliness criticality in complex systems. Nat. Phys. 20, 1352–1358 (2024). https://doi.org/10.1038/s41567-024-02525-w
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41567-024-02525-w
This article is cited by
-
Critical delay accumulation
Nature Physics (2024)
-
Too much efficiency leads to delays
Nature Reviews Physics (2024)