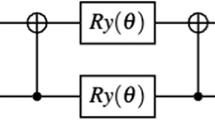
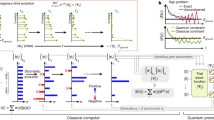
Abstract
Quantum computational chemistry has emerged as a potential application of quantum computing. Hybrid quantum-classical computing methods, such as variational quantum eigensolvers, have been designed as promising solutions to quantum chemistry problems. Nonetheless, challenges due to theoretical complexity and experimental imperfections hinder progress in achieving reliable and accurate results. Experimental works for solving electronic structures are consequently still restricted to non-scalable or classically simulable ansatz or limited to a few qubits with large errors. Here, we address the critical challenges associated with solving molecular electronic structures using noisy quantum processors. Our protocol presents improvements in the circuit depth and running time, key metrics for chemistry simulation. Through systematic hardware enhancements and the integration of error-mitigation techniques, we overcome theoretical and experimental limitations and successfully scale up the implementation of variational quantum eigensolvers with an optimized unitary coupled cluster ansatz to 12 qubits. We produce high-precision results of the ground-state energy for molecules with error suppression by around two orders of magnitude. Our work demonstrates a feasible path towards a scalable solution to electronic structure calculation.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Source data are provided with this paper. All other data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The code for this paper is available from the corresponding authors upon reasonable request.
References
Aspuru-Guzik, A., Dutoi, A. D., Love, P. J. & Head-Gordon, M. Simulated quantum computation of molecular energies. Science 309, 1704–1707 (2005).
Lanyon, B. P. et al. Towards quantum chemistry on a quantum computer. Nat. Chem. 2, 106–111 (2010).
Argüello-Luengo, J., González-Tudela, A., Shi, T., Zoller, P. & Cirac, J. I. Analogue quantum chemistry simulation. Nature 574, 215–218 (2019).
Reiher, M., Wiebe, N., Svore, K. M., Wecker, D. & Troyer, M. Elucidating reaction mechanisms on quantum computers. Proc. Natl Acad. Sci. USA 114, 7555–7560 (2017).
Cao, Y. et al. Quantum chemistry in the age of quantum computing. Chem. Rev. 119, 10856–10915 (2019).
McArdle, S., Endo, S., Aspuru-Guzik, A., Benjamin, S. C. & Yuan, X. Quantum computational chemistry. Rev. Mod. Phys. 92, 015003 (2020).
Bauer, B., Bravyi, S., Motta, M. & Chan, G. K.-L. Quantum algorithms for quantum chemistry and quantum materials science. Chem. Rev. 120, 12685–12717 (2020).
Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213 (2014).
Cerezo, M. et al. Variational quantum algorithms. Nat. Rev. Phys. 3, 625–644 (2021).
Bharti, K. et al. Noisy intermediate-scale quantum algorithms. Rev. Mod. Phys. 94, 015004 (2022).
Dalton, K. et al. Quantifying the effect of gate errors on variational quantum eigensolvers for quantum chemistry. npj Quantum Inf. 10, 18 (2024).
Bittel, L. & Kliesch, M. Training variational quantum algorithms is np-hard. Phys. Rev. Lett. 127, 120502 (2021).
Gonthier, J. F. et al. Measurements as a roadblock to near-term practical quantum advantage in chemistry: resource analysis. Phys. Rev. Res. 4, 033154 (2022).
Yen, T.-C., Ganeshram, A. & Izmaylov, A. F. Deterministic improvements of quantum measurements with grouping of compatible operators, non-local transformations, and covariance estimates. npj Quantum Inf. 9, 14 (2023).
Stilck França, D. & Garcia-Patron, R. Limitations of optimization algorithms on noisy quantum devices. Nat. Phys. 17, 1221–1227 (2021).
Wang, S. et al. Noise-induced barren plateaus in variational quantum algorithms. Nat. Commun. 12, 6961 (2021).
O’Malley, P. J. et al. Scalable quantum simulation of molecular energies. Phys. Rev. X 6, 031007 (2016).
Hempel, C. et al. Quantum chemistry calculations on a trapped-ion quantum simulator. Phys. Rev. X 8, 031022 (2018).
Colless, J. I. et al. Computation of molecular spectra on a quantum processor with an error-resilient algorithm. Phys. Rev. X 8, 011021 (2018).
Nam, Y. et al. Ground-state energy estimation of the water molecule on a trapped-ion quantum computer. npj Quantum Inf. 6, 33 (2020).
Shen, Y. et al. Quantum implementation of the unitary coupled cluster for simulating molecular electronic structure. Phys. Rev. A 95, 020501 (2017).
Kandala, A. et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549, 242–246 (2017).
Arute, F. et al. Hartree-Fock on a superconducting qubit quantum computer. Science 369, 1084–1089 (2020).
Kandala, A. et al. Error mitigation extends the computational reach of a noisy quantum processor. Nature 567, 491–495 (2019).
Quek, Y., França, D. S., Khatri, S., Meyer, J. J. & Eisert, J. Exponentially tighter bounds on limitations of quantum error mitigation. Preprint at https://arXiv.org/2210.11505 (2022).
Romero, J. et al. Strategies for quantum computing molecular energies using the unitary coupled cluster ansatz. Quantum Sci. Technol. 4, 014008 (2018).
Anand, A. et al. A quantum computing view on unitary coupled cluster theory. Chem. Soc. Rev. 51, 1659–1684 (2022).
Bartlett, R. J., Kucharski, S. A. & Noga, J. Alternative coupled-cluster ansätze II. The unitary coupled-cluster method. Chem. Phys. Lett. 155, 133–140 (1989).
Bravyi, S., Sheldon, S., Kandala, A., Mckay, D. C. & Gambetta, J. M. Mitigating measurement errors in multiqubit experiments. Phys. Rev. A 103, 042605 (2021).
Czarnik, P., Arrasmith, A., Coles, P. J. & Cincio, L. Error mitigation with clifford quantum-circuit data. Quantum 5, 592 (2021).
Lowe, A. et al. Unified approach to data-driven quantum error mitigation. Phys. Rev. Res. 3, 033098 (2021).
Cioslowski, J. Connected moments expansion: a new tool for quantum many-body theory. Phys. Rev. Lett. 58, 83–85 (1987).
Claudino, D., Peng, B., Bauman, N. P., Kowalski, K. & Humble, T. S. Improving the accuracy and efficiency of quantum connected moments expansions. Quantum Sci. Technol. 6, 034012 (2021).
Stanton, J. F., Gauss, J., Watts, J. D. & Bartlett, R. J. A direct product decomposition approach for symmetry exploitation in many-body methods. I. Energy calculations. J. Chem. Phys. 94, 4334–4345 (1991).
Cao, C. et al. Progress toward larger molecular simulation on a quantum computer: simulating a system with up to 28 qubits accelerated by point-group symmetry. Phys. Rev. A 105, 062452 (2022).
Fan, Y. et al. Circuit-depth reduction of unitary-coupled-cluster ansatz by energy sorting. J. Phys. Chem. Lett. 14, 9596–9603 (2023).
Schuld, M., Bergholm, V., Gogolin, C., Izaac, J. & Killoran, N. Evaluating analytic gradients on quantum hardware. Phys. Rev. A 99, 032331 (2019).
Wecker, D., Hastings, M. B. & Troyer, M. Progress towards practical quantum variational algorithms. Phys. Rev. A 92, 042303 (2015).
Wu, B., Sun, J., Huang, Q. & Yuan, X. Overlapped grouping measurement: a unified framework for measuring quantum states. Quantum 7, 896 (2023).
Huang, H.-Y., Kueng, R. & Preskill, J. Efficient estimation of pauli observables by derandomization. Phys. Rev. Lett. 127, 030503 (2021).
Gustavsson, S. et al. Dynamical decoupling and dephasing in interacting two-level systems. Phys. Rev. Lett. 109, 010502 (2012).
Bonet-Monroig, X., Sagastizabal, R., Singh, M. & O’Brien, T. E. Low-cost error mitigation by symmetry verification. Phys. Rev. A 98, 062339 (2018).
Wu, Y. et al. Strong quantum computational advantage using a superconducting quantum processor. Phys. Rev. Lett. 127, 180501 (2021).
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Tilly, J. et al. The variational quantum eigensolver: a review of methods and best practices. Phys. Rep. 986, 1–128 (2022).
Sun, Q. et al. Pyscf: the Python-based simulations of chemistry framework. Wiley Interdiscip. Rev. Comput. Mol. Sci. 8, e1340 (2018).
Rubin, N. C. et al. The fermionic quantum emulator. Quantum 5, 568 (2021).
Hadfield, C., Bravyi, S., Raymond, R. & Mezzacapo, A. Measurements of quantum Hamiltonians with locally-biased classical shadows. Commun. Math. Phys. 391, 951–967 (2022).
O’Brien, T. E. et al. Purification-based quantum error mitigation of pair-correlated electron simulations. Nat. Phys. 19, 1787–1792 (2023).
Zhao, L. et al. Orbital-optimized pair-correlated electron simulations on trapped-ion quantum computers. npj Quantum Inf. 9, 60 (2023).
Acknowledgements
We thank W. Li, V. Vedral, M.S. Kim, H. Shen, C. Cao, D. Lv and J. Liu for useful related discussions on the theoretical scheme. We thank the USTC Center for Micro- and Nanoscale Research and Fabrication for supporting the sample fabrication. We also thank QuantumCTek Co., Ltd. for supporting the fabrication and maintenance of room-temperature electronics. This research was supported by the Innovation Programme for Quantum Science and Technology (grant nos. 2021ZD0300200, 2023ZD0300200), Shanghai Municipal Science and Technology Major Project (grant no. 2019SHZDZX01), Anhui Initiative in Quantum Information Technologies, National Natural Science Foundation of China (grant nos. 12175003 and 12361161602), NSAF (grant no. U2330201), Natural Science Foundation of Shandong Province, China (grant no. ZR202209080019), the Key-Area Research and Development Programme of Guangdong Province (grant no. 2020B0303060001) and special funds from Jinan Science and Technology Bureau and Jinan High Tech Zone Management Committee. H.-L.H. acknowledges support from the Youth Talent Lifting Project (grant no. 2020-JCJQ-QT-030), National Natural Science Foundation of China (grant nos. 11905294, 12274464), China Postdoctoral Science Foundation and the Open Research Fund from State Key Laboratory of High Performance Computing of China (grant no. 201901-01). J.S. acknowledges the Samsung GRC grant for financial support. M.G. was supported by the National Science Foundation of China (grant no. T2322024), Shanghai Rising-Star Programme (grant no. 23QA1410000) and the Youth Innovation Promotion Association of CAS (grant no. 2022460). X.Z. acknowledges support from THE XPLORER PRIZE.
Author information
Authors and Affiliations
Contributions
X.Y, M.G and J.S. initiated the project. J.S. developed the theoretical aspect of the project and built up the source code for numerical simulation with input from X.Y. and Y. Zhang. J.S., Y. Zhang and K.L. carried out the numerical simulation under the supervision of X.Y., Y. Zhang and K.L. generated the measurement bases with the algorithm developed by J.S. S.G., H.Q., M.G., F.C. and S.C. performed the measurements. S.G., J.S., H.Q., M.G. and Y. Zhao analysed the experimental data. Q.Z., Y.Y., C.Y., F.C. and S.L. designed the processor. S.C., Y.L., K.Z., S.G., H.Q., T.-H.C., H.R., H.D. and Y.-H.H. fabricated the processor. M.G., S.W., C.Z., Y. Zhao, S.L., C.Y., J.Y., D.F., D.W. and H.S. contributed to the construction of the ultracold and low-noise measurement system. J.L., Y.X., F.L., C.G., L.S., N.L. and C.-Z.P. developed the room-temperature electronics. Experiments were performed using a quantum processor that was developed and fabricated with a large effort from the experimental team. J.S., S.G., Y.Z., X.Y. and M.G. wrote the paper with input from all authors. X.Y., X.Z. and J.-W.P. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Christian Andersen and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Benchmark of multi-qubit Pauli rotation gate.
The comparison of the operation quality before and after optimization with qubit number being four (a), six (b), eight (c) and ten (d). The error rate of each sequence, as a characteristic of the averaged fidelity, can be obtained by measuring the probability of \({\left\vert 0\right\rangle }^{\otimes n}\). The data points are the average values at each sequence length.
Supplementary information
Supplementary Information
Supplementary Figs. 1–15, discussion and Table I.
Source data
Source Data Fig. 2
Statistical source data.
Source Data Fig. 3
Statistical source data.
Source Data Fig. 4
Statistical source data.
Source Data Extended Data Fig. 1
Statistical source data.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Guo, S., Sun, J., Qian, H. et al. Experimental quantum computational chemistry with optimized unitary coupled cluster ansatz. Nat. Phys. 20, 1240–1246 (2024). https://doi.org/10.1038/s41567-024-02530-z
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41567-024-02530-z
This article is cited by
-
Observable-driven speed-ups in quantum simulations
Communications Physics (2025)
-
Measuring correlation and entanglement between molecular orbitals on a trapped-ion quantum computer
Scientific Reports (2025)
-
Experimental implementation of a qubit-efficient variational quantum eigensolver with analog error mitigation on a superconducting quantum processor
Science China Physics, Mechanics & Astronomy (2025)
-
Non-hemolytic peptide classification using a quantum support vector machine
Quantum Information Processing (2024)