Main

The transient change and control of the optical properties of matter by X-ray irradiation have led to a new area of nonlinear optical physics accessible through the development of X-ray free-electron lasers (XFELs). These sources provide intense femtosecond X-ray pulses that can drive solids out of equilibrium to induce nonlinear multiphoton effects such as saturable absorption (SA), through which, for example, a metal transiently becomes transparent in specific spectral regions1,2,3,4, or its counterpart, reverse saturable absorption (RSA), during which absorption increases with increasing intensity5. SA occurs when the absorbing state of a material is depleted (by absorption of a high photon flux) at a faster rate than it is replenished, thus causing the absorption to saturate. RSA occurs when the excited state of a material has a larger absorption cross section than the ground state. The temporal and spectral properties of the light pulse inducing SA or RSA undergo drastic alterations. Both effects are routinely used in the optical regime for applications such as mode-locking, pulse-shaping and two-photon microscopy6,7,8, with possible transitions between these regimes9,10. Transferring them to the X-ray spectral domain could be a route to controlled X-ray pulse-shaping2,11,12. Previous studies of XFEL-irradiated matter reporting SA or RSA have mostly relied on spectrally integrated measurements1,3,5. Here, we present spectrally resolved measurements of the transition from RSA to SA over a large span of applied X-ray intensities.

The solid target undergoing such intense X-ray irradiation transiently transforms into warm dense matter (WDM), a state that is too hot to be described by condensed matter physics yet too dense to be described by weakly coupled plasma physics (for a review, see, for example, ref. 13). Although there has been progress in understanding the thermodynamic and steady state structural properties of WDM in the last decade, both experimentally (for example, refs. 14,15) and theoretically (for example, ref. 16), studying the non-equilibrium electron dynamics and structural changes following an external XFEL excitation still poses great challenges. So far, X-ray emission spectroscopy has been the method of choice for revealing the evolution of XFEL-created WDM17,18,19,20, estimating collisional ionization rates21,22 and studying the ionization potential depression23,24. A complementary technique, time-resolved X-ray absorption near-edge structure spectroscopy (XANES), is a powerful tool for simultaneously probing the valence electron state and the atomic structure25. Until now, XANES has mostly been applied to infrared- and optically heated WDM with picosecond to subpicosecond time resolution26,27,28,29,30,31.

Here, we take advantage of the full spectral bandwidth of XFEL pulses created by the self-amplified spontaneous emission to study the formation of warm dense copper with XANES. We use a 15-fs-long XFEL pulse to excite and probe a 15-eV-wide spectral window across the Cu L2 (952 eV) and L3 (932 eV) edges. In both cases, direct 2p photoionization above the edge followed by Auger decay and electron impact ionization are the main excitation mechanisms that lead to the creation of 3d vacancies (Fig. 4). The latter strongly influence the overall absorption of the pulse through resonant 2p → 3d transitions of several ionic species that fit into the probed spectral window. By varying the XFEL intensity, we demonstrate the transition from RSA to SA in the X-ray regime, here at the Cu L2 and L3 edges. Such a transition was predicted in aluminium by Cho et al.5,11 but has so far never been observed due to the lack of sufficient XFEL intensity. Our observations are verified by theoretical modelling of the transient absorption using Boltzmann kinetic equations to follow the evolution of the electronic configurations and high-temperature XANES calculations using the real-space Green’s function code FEFF10 (ref. 32).

Spectral observations of XFEL-created WDM

Absorption spectra (see Methods for details) for a 100-nm-thick Cu film with XFEL pulses tuned to the L3 absorption edge are shown in Fig. 1 for various pulse intensities I. For intensities I ≥ 1 × 1013 W cm−2, the absorption increases in the spectral region below the edge. This pre-edge peak is well known25,28,29,30,31 and is due to 3d vacancies, which trigger photoabsorption through 2p3/2 → 3d transitions. The pre-edge absorption drastically increases with pulse intensity to become 2.5 times larger than the cold L3 edge amplitude at Itr = 1 × 1015 W cm−2. This increase is accompanied by a shift of the maximum of the peak towards lower energies (redshift) due to screening effects, which are discussed in detail later. For intensities I > Itr, further ionization broadens and shifts the spectrum maximum to higher energy (blueshift) due to reduced screening of the nuclear charge, as discussed below. The overall absorption then decreases. At the highest pulse intensity, the L3 edge cannot be clearly resolved. A moderate, monotonic increase of absorption with photon energy is observed across the entire energy range probed.

Fig. 1: Transient XANES of XFEL-created warm dense copper.
figure 1

a, Experimental absorption spectra of 100-nm-thick film at the L3 edge are shown for various XFEL intensities, as indicated in the figure, in W cm−2. The spectra are vertically offset by 7 μm−1. The coloured areas around each spectrum indicate the 95% confidence intervals. The red (blue) areas show the stronger (weaker) absorption relative to the cold spectrum obtained at I = 5 × 1012 W cm−2. The dashed line indicates the position of the pre-edge peak at low intensity. The arrow shows the characteristic peak originating from the zero-temperature van Hove singularity density of states of Cu. b, Corresponding theoretical XANES calculations as discussed in the text.

Source data

Full size image

Another distinct feature of the spectrum is an ~1-eV-wide peak centred at 936.7 eV, as indicated by the black arrow in Fig. 1. This peak is a signature of a van Hove singularity in the density of states of the face-centred cubic crystalline phase of copper, which reflects the long-range crystalline order33,34. It has been shown to disappear upon melting in an optically excited pump–probe experiment30, which indicates the loss of crystal order25,34. In our case, the pulse duration of 15 fs is so short that no structural change involving ion motion takes place, an assumption corroborated by our observation of the van Hove peak up to intensities of 1 × 1014 W cm−2. At higher intensities, the peak is suppressed by several broadening mechanisms and becomes buried in the spectral region of the shifting pre-edge feature. The redistribution of the electronic states is then so strong (see discussions below) that the van Hove singularity of cold copper is no longer reliable for analysing the crystalline structure. At the highest intensity of 7 × 1017 W cm−2, the peak has disappeared.

We also measured a series of spectra at the L2 edge (Supplementary Fig. 2). The L2 and L3 edges have similar structures34 with an energy shift of 20 eV, but their intensities differ by a factor of 2 (the statistical branching ratio). The observed trends are summarized in Fig. 2a, in which the variations of the XFEL pulse transmission are plotted against intensity (see Methods for details). At the L3 edge, the transmission as a function of intensity is constant up to 1.6 × 1013 W cm−2. It decreases to a minimum at a transition intensity Itr = 1 × 1015 W cm−2 and increases again for higher intensities. Similar behaviour is observed at the L2 edge but shifted to higher intensities, with Itr = 1 × 1016 W cm−2. Looking at spectral regions centred below, on and above the L2 and L3 edges, we follow the spectrally resolved variation of transmission in Fig. 2b–e. A transmission minimum is observed in all regions considered except for region 1 (below the L3 pre-edge), but the intensity at which it occurs is higher for regions with higher photon energies. These observations are discussed in detail below. Note that the transmission level below the L3 edge at low intensity is, as expected, close to that of a cold target (87% for 100 nm; ref. 35). More measurements of the 500-nm-thick sample are presented in Supplementary Information Section II.

Fig. 2: Transition from RSA to SA.
figure 2

a, Transmission of an XFEL pulse centred at the L2 and L3 edges of a 100-nm-thick Cu foil as a function of pulse intensity I. In both cases, the transmission first decreases (RSA), reaches a minimum and then increases (SA) as a function of intensity. b,c, Transmission at the L3 edge (b) and L2 edge (c) in selected spectral regions below the L3 or L2 pre-edge (1,4), on the L3 or L2 pre-edge (2, 5) and on the L3 or L2 edge (3, 6), respectively, as shown in corresponding panels d and e. d,e, The solid lines show the cold reference spectra (absorption coefficient μA) whereas the dotted lines show spectra where the pre-edge features are prominent, as obtained at I = 5 × 1013 W cm−2 (d) and I = 9 × 1014 W cm−2 (e). The vertical dashed lines, labelled 3dN, show the calculated 2p3/23dN → 3dN+1 excitation energies of various ions (Supplementary Information Section VI.B). The error bars in a, b and c indicate the 95% confidence intervals.

Source data

Full size image

Theoretical description of XFEL-created WDM

Modelling the XANES structure of WDM in a state out of equilibrium is challenging. Heretofore, there has been no ab initio electronic structure theory capable of predicting XANES structures for the presented non-equilibrium regime. The challenge can be approached either from the plasma state or from the solid state. On the one hand, a plasma-state description can teach us about ionization dynamics, electron configurations and non-equilibrium electron energy distributions36. However, it inherently lacks any description of bonding and hybridization of states and electronic bands that are crucial for XANES calculations. On the other hand, if inelastic effects are neglected, XANES structures of states under electronic equilibrium, for which an electronic temperature can be defined, can be tackled by finite-temperature density-functional theory (DFT)37. However, a direct extension of the principal foundations of DFT to non-equilibrium electron energy distributions has yet to be developed. Nevertheless, ad hoc extensions of DFT methods involving two non-equilibrium electronic temperatures31, a non-thermal lattice38 or that go beyond the frozen core approximation39 can be attempted for transient states of WDM out of electronic equilibrium. Moreover, finite-temperature quasiparticle approaches have recently been developed for equilibrium XANES calculations up to the WDM regime40,41.

Here, we present an approach that combines a plasma description of X-ray-excited copper based on kinetic Boltzmann equations42,43,44 with finite-temperature extensions of DFT. We use the FEFF10 code32 to capture the solid-state electronic structure and calculate the absorption spectrum. Briefly, the overall approach for simulating X-ray absorption is as follows. First, the Boltzmann equation solver was used to characterize the state of the system, that is, to predict the relative abundance of various atomic configurations in the system, as a function of time and XFEL intensity. Next, for each time and intensity, the FEFF10 real-space multiple-scattering code was used to calculate the absorption due to each of the relevant configurations, with the surroundings approximated by atoms at the crystal lattice and with 3d occupation set to the average 3d occupation obtained from the Boltzmann model. An effective 3d-band temperature was introduced to fix the average 3d occupation within FEFF (Supplementary Fig. 15) and allow for self-consistent relaxation of the electron density. Finally, the total absorption was calculated as an average over space and time of the contributions from all relevant configurations, weighted by the pulse intensity. Details of the theory and calculations can be found in Supplementary Information Section VI. Due to space limitations, we restrict our analysis here to a 100-nm-thick Cu film irradiated at the L3 edge.

The Boltzmann kinetic equation solver (see Methods for details) follows the non-equilibrium evolution of emerging free-electron densities and active atomic configuration densities resulting from photoionization, Auger decays and subsequent electronic collisional processes. Detailed results obtained with the model can be found in Supplementary Figs. 9–12. The most populated Cu configurations over the pulse duration mainly consist of various 3d shell occupations, although the configurations with 3p shell vacancies can also appear at very high intensities, as shown in Fig. 3. The model also follows the non-equilibrium evolution of the transient electron energy distribution ρe(E), as illustrated for I = 5 × 1012 W cm−2 and I = 1 × 1017 W cm−2 in Fig. 4a,b, respectively. Initially, photoionization and Auger electron peaks are present in the high-energy regions of the spectra for both low and high X-ray intensities. For a low X-ray intensity (Fig. 4a), the electronic distribution below ~30 eV increases with time and almost stabilizes after 10 fs. It approaches a Maxwell–Boltzmann distribution, but the peak distribution in the high-energy range remains at 20 fs. This shows that the electronic system has still not equilibrated after the pulse has passed. For a high X-ray intensity (Fig. 4b), the situation is different. The peaks in the high-energy range are quickly redistributed between −20 and −10 fs due to efficient electron–electron interactions, which increase the overall kinetic electron energy. At 10 fs, the electron distribution has already thermalized into a Maxwell–Boltzmann distribution. The simulation thus suggests that our time-integrated XANES measurements contain notable contributions from the non-equilibrium evolution stages.

Fig. 3: Electronic configurations of XFEL-created warm dense copper.
figure 3

a–c, Relative abundances of the most populated Cu configurations averaged over the pulse duration, obtained from the kinetic Boltzmann calculations, for different pulse intensities I and plotted against the number of 3d electrons N. The base electronic configurations are [Ar] 4s13dN (a), [Ne] 3s23p54s13dN (b) and [Ne] 3s23p54s13dN (c).

Full size image
Fig. 4: Evolution of the free-electron energy distribution.
figure 4

a,b, Evolution of the transient electron energy distribution ρe(E) in XFEL-irradiated Cu with pulse intensity I = 5 × 1012 W cm−2 (a) and pulse intensity I = 1 × 1017 W cm−2 (b). The curves represent the electron distributions at various time instants with time zero corresponding to the maximum of the 15 fs FWHM Gaussian pulse. ρe is defined by ∫ρe(E)dE = 〈Z〉 where 〈Z〉 denotes the transient ionization degree per atom, that is, the number of free electrons above the vacuum level divided by the total number of atoms. The black dashed curves show the Maxwell–Boltzmann (MB) distributions with a kinetic temperature equal to the average electron kinetic energy at 20 fs: 2.2 eV (a) and 90 eV (b). The broad peak with a substructure at around 250 eV, as indicated by a blue arrow, corresponds to the secondary electron emission during the collisional ionization of neutral Cu and Cu+ ground states. The sharp peak at 943 eV, as indicated by a red arrow, is due to the Auger decay of the 2p3/2 core hole.

Full size image

The absorption cross section at a specific instant in time and point in space depends both on the electronic configuration of the absorbing atom and on the state of the surrounding system. Absorption at the L3 edge is simulated for each atom in the system at time t, with initial configurations taken from the Boltzmann model. In the final state of absorption, the atom has a hole in the 2p3/2 orbital. We neglect the atoms with initial configurations containing holes in deeper shells than 3d, as their contributions are relevant only at very high intensities, I ≥ 3 × 1016 W cm−2 (Fig. 3 and Supplementary Fig. 13). The environment of the absorbing atom is accounted for by introducing an effective electronic temperature Teff, chosen such that the average 3d-band occupation given by a self-consistent solid-state calculation matches that given by the kinetic Boltzmann simulations at time t for a given X-ray intensity. The temperature Teff was found to be in good agreement with the kinetic temperature reached at the end of the pulse from Boltzmann simulations. The transient absorption cross sections for each configuration λ of the absorbing atom are then calculated over a range of Teff (Supplementary Fig. 19) and weighted by the relative abundances pλ resulting from the Boltzmann simulations to determine the total absorption cross section σ(ω, x, y, z, t) = ∑λpλ(x, y, z, t)σλ(ω, Teff), where ω is the incoming photon frequency and (x, y, z) are the atom coordinates. To provide a gauge of the reliability of the approach, we compare it in the Supplementary Information to a second calculation that neglects the variations of the surrounding system with intensity but better accounts for the density and potential of the absorbing atom. We found that this calculation also qualitatively explains the observed trends but cannot predict the observed redshift at low to moderate intensities.

Interpretation of XANES spectra

Figure 1 compares the calculated XANES spectra to the experimental results. The theory confirms that there is a transition from RSA at low to intermediate intensities to SA at the highest intensity. RSA is evidenced by the appearance of the pre-edge peak arising from the growing probability of resonant absorption by 2p63d9 atoms at low intensity. Not only does the pre-edge peak grow, but it also extends towards lower energy and shows a redshift, as in the experimental observations (Supplementary Fig. 7). Physically, several effects contribute to this net energy shift. First, the valence electron density of states (3d-DOS) is partially depopulated by the initial fraction of the pulse, starting from the most energetic electrons close to the Fermi level EF and continuing with less energetic electrons. Consequently, as the XFEL pulse intensity is increased, the number of unoccupied 3d states probed by the remainder of the pulse increases and their average energy is reduced, as seen in Fig. 5a, which shows the redshift of the Fermi energy for different configurations. Second, as Teff increases, the partial depopulation of the 3d-DOS induces a reduction of the electronic screening of the nuclear charge, which increases the electron–ion potential and leads to a dramatic redshift of the 3d band of the order of a few electronvolts to tens of electronvolts, as seen in Fig. 5b and in agreement with previous studies25,30,31,45,46. However, the observed net shift is much smaller (<1 eV). This is because the reduction of the electronic screening also affects the bound (2p) electron levels by a comparable amount41,46. In fact, the shift of the 2p levels dominates for highly ionized atoms and leads to blueshifted excitation energies (Fig. 2d,e and Supplementary Fig. 16). Finally, the width of the 3d band shrinks with increasing Teff (Fig. 5b). Because of this, in our calculations, the distance between the centroid of the 3d band (which is used to align the spectra) and the chemical potential for a given configuration decreases as Teff is increased to produce an additional redshift for higher 3d occupation, for example, 3d9 and 3d10.

Fig. 5: Influence of temperature on 3d-DOS.
figure 5

a, Occupied 3d-DOS calculated at room temperature (0.025 eV) for different configurations, which was used to find the chemical potential μλ for each configuration. The total 3d-DOS is also shown for comparison. Similar 3d-DOS data exist for each effective temperature Teff(n) for each 3d-band occupancy. b, 3d-DOS as a function of energy relative to the vacuum level E at different effective temperatures.

Full size image

As the intensity is increased, we observe the continued growth, broadening and merging of this pre-edge peak with the cold edge (Fig. 1). This evolution is due to the increased probability of absorption from atoms with eight or fewer electrons in the 3d shell. These states have blueshifted excitation energies with broadened absorption profiles (Supplementary Figs. 16–18). Thus, for increasing intensity and depletion of the 3d states, the pre-edge absorption peak shifts to the blue end of the spectrum. Eventually the absorption lines move beyond the spectral window of the applied field (closing of absorption channels resulting in SA). This is why both the onset of RSA and the RSA to SA transition shift to higher intensities at higher photon energies. This can be seen in Fig. 2b,c by comparing region 2 with region 3 and region 5 with region 6. In addition, the van Hove peak decreases with intensity. Theoretical predictions indicate that it becomes negligible at 5 × 1015 W cm−2. Our experiment confirms it at 7 × 1017 W cm−2. This effect is also due to the modifications of the excited 3d band, which drastically alter the absorption spectrum for each configuration (Supplementary Fig. 17).

Despite the overall qualitative agreement in the trends of the XANES versus pulse intensity between theory and experiment, some discrepancies are notable. In particular, the calculated RSA to SA transition occurs at higher intensity than experimentally observed. Several factors contribute to this disagreement. One is the experimental characterization of the beam intensity, which can differ by approximately 50% (Methods). Another is the restricted accuracy in the description of the state of the system by a plasma approach (here, the Boltzmann model). We discuss in detail the limitations of this model in Supplementary Information Section V.B. In addition, at low to intermediate intensities, the predicted redshift of the pre-edge peak is not as large as experimentally observed. This could be an indication that the calculation of the excitation energies is incorrect. At higher intensities, the blueshift is not seen in the peak of the theoretical spectrum. If one considers the centroid of the peak, a blueshift is evident but appears at much higher intensities than those seen in the experiment. This could again be linked to a mismatch between the relative abundance of different ionic states predicted by the Boltzmann model and that present in the real system. Another possible contribution could be an overestimate of the broadening used in the calculations. This could be due to the lack of solid-state effects in the estimate of atomic multiplet splitting, which are known to reduce the effect of e–e Coulomb interactions47, or the use of an equilibrium distribution to describe free electrons when calculating the interaction between the photoelectron and the free electrons. One other noticeable disagreement between experiment and theory is that at intermediate to high intensities, the absorption cross section predicted by the theory at high energy (~938 to 940 eV) is reduced compared to the ambient system, whereas the experimental cross section shows little to no change. This points to the possibility that it is incorrect to use an equilibrium electron distribution when calculating the cross section.

The L2 edge spectral region is even more complex but can be described qualitatively now that we have established the link between the blueshift of the XANES spectrum and the appearance of higher charge states. Not only does the bandwidth of the pulse contain the 2p1/2 → 3d absorption channels of the 3d9 ion but also the 2p3/2 → 3d channels of several higher ionic species, as shown in Fig. 2e. Therefore, as the pulse intensity and the ionization degree are increased, the saturation of 2p1/2 → 3d absorption by Cu+ is compensated for by 2p3/2 → 3d absorption by higher charge states. This effect can be observed by comparing the evolution of spectral regions 1 and 4 in Fig. 2. Below the pre-edge absorption peak of L3 (region 1), the transmission as a function of pulse intensity remains constant, within the measurement error. In contrast, the transmission in region 4 sharply decreases between I = 5 × 1015 and 1 × 1016 W cm−2. This sudden change is attributed to the opening of 2p3/2 → 3d absorption channels in Cu4+, Cu5+ and Cu6+. These other channels contribute to the overall absorption in the L2 spectral region. They are why the transition from RSA to SA at the L2 edge is shifted to higher intensity compared to that at the L3 edge.

Outlook

The experimental method presented uses averaged signal and reference spectra, but a self-referencing scheme could substantially increase the signal-to-noise ratio48. Besides, the scheme can be extended to X-ray pump and X-ray probe XANES using the two-colour mode available at current XFEL facilities49. This would allow us to follow the evolution of the WDM state in a time-resolved manner. Recall that the time resolution of our method is limited only by the pulse duration. The prospect of attosecond XFEL pulses and attosecond transient XANES capabilities will further widen the applicability of the presented approach in the study of matter under extreme conditions.

Methods

Experimental set-up

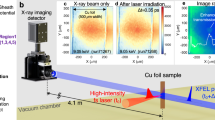
The experiment was performed at the Spectroscopy and Coherent Scattering (SCS) instrument of the European XFEL (EuXFEL). The XFEL pulse energy was measured with two X-ray gas monitors, one before beam transport and the other one in the SCS instrument hutch, just upstream of the focusing optics. A gas attenuator filled with N2 at an adjustable pressure allowed the pulse energy to be controlled. The beam was focused by Kirkpatrick–Báez mirrors. The beam size of 4 μm full-width at half-maximum (FWHM) was characterized by a knife-edge scan. With a pulse energy of up to 2 mJ measured at the SCS X-ray gas monitor, an intensity of ~7 × 1017 W cm−2 was achieved on sample. The accuracy of the intensity reached was estimated to be ~25% based on the uncertainty of the measurements by the X-ray gas monitors, the transmission of the Kirkpatrick–Báez mirrors and the knife-edge beam size characterization. A pulse duration of 15 fs FWHM was derived from a spectral correlation analysis (see Supplementary Information for details). The irradiated sample was a 100- or 500-nm-thick copper foil supported by a nickel mesh. Great care was taken in the fabrication (by Luxel) and handling of the experimentally studied samples, and no sign of oxidation was found, as evidenced by the absence of a pre-edge peak characteristic of CuO or Cu2O in the low-intensity limit spectra. The sample was rastered to a pristine region for every shot at the 10 Hz train repetition rate of EuXFEL, and the spectra where the beam hit the mesh were discarded in the following way. As the mesh was 15 μm thick, it fully blocked the X-ray pulse upon irradiation, even at the highest irradiation intensities. The spectra where the mesh was hit were filtered out by setting a threshold on the intensity of the integrated spectrum below which the pulse was considered to have hit the mesh. In addition, the position of the stage was recorded and corroborated with the threshold analysis. Finally, a post-mortem analysis with an optical microscope allowed us to reliably confirm the data sorting. The very few points (approximately less than 1% of the number of pulses per XANES spectrum) where a Ni mesh hit was not clear were discarded. The spectrometer50 was placed 2.3 m downstream of the interaction point and consisted of an entrance slit of 40 μm and a grating with 1,200 lines per mm. It had a radius of curvature of 5 m in the Rowland geometry and was coupled to a CCD camera (Andor, model Newton). The energy was calibrated using the beamline monochromator51. The low-fluence limit spectra were found to be in good agreement with those in refs. 28,30. The resolving power was E/ΔE ≈ 2,400. To avoid saturation of the detector, the transmitted beam was attenuated by a combination of Al filters of 3.5, 5 or 10 μm thickness upstream of the entrance slit of the spectrometer.

Absorption spectra

Ultrashort pulses from EuXFEL were tightly focused onto a thin Cu foil. Their energy levels were tuned at the L2 edge (952 eV) or L3 (932 eV) edge, with ~40% of their spectral content above the edge. The total bandwidth was ~0.7% FWHM. The spectrum of an XFEL pulse contains randomly distributed spikes originating from the self-amplification of the spontaneous emission process, such that averaging over many shots is necessary for a meaningful comparison of spectra with and without a sample. Examples of single-shot and average spectra are shown in Supplementary Fig. 1. For each experimental condition, including the low-intensity limit, ~2,000 single-shot spectra were recorded without a sample and 200 to 1,000 single-shot spectra recorded with a sample. The drifts of the photon energy and pulse energy between two data acquisitions were small enough to be neglected. The absorption coefficient was then calculated for each photon energy as \({\mu }_\mathrm{A}=\ln ({I}_\mathrm{ref}/{I}_\mathrm{Cu})/d\), where Iref is the averaged reference spectrum intensity, ICu is the averaged spectrum intensity with a sample and d is the sample thickness.

Transmission of the XFEL pulse

The integral over the entire bandwidth of the spectra without a sample Sref or with a sample SCu is proportional to the total number of photons of the incoming or transmitted pulse, respectively. The total transmission is, thus, T = 〈SCu〉/〈Sref〉, where 〈…〉 is the average over the number of collected spectra of a given pulse intensity. Likewise, a spectrally resolved transmission can be defined within a specific photon-energy window of the spectra.

Pre-edge shift

The energy shift of a pre-edge feature (Supplementary Fig. 7) was extracted by determining the position of the zero-crossing of the derivative of the absorption spectra smoothed using a Savitzky–Golay filter. Given the spectrometer dispersion and the error bar in the absorption spectra, the position accuracy varied from ±0.22 to ±0.11 eV.

Boltzmann kinetic equations

The Boltzmann kinetic equation solver models the interaction of an X-ray pulse with a bulk material. The X-ray pulse was assumed to have a temporal Gaussian profile of 15 fs FWHM. It was also assumed to be monochromatic, with photon energy ~1 eV above the L3 cold edge. This approximation is justified by the slow variations of the absorption cross sections below and above the edge. In Supplementary Information Section II, we discuss the differences between excitation below and above the L3 edge. The classical Boltzmann kinetic equations originate from the reduced N-particle Liouville equations and include only single-particle phase-space densities of charge states and free electrons in the sample. The Boltzmann equation solver, originally constructed to follow the non-equilibrium evolution of finite systems (for example, atomic clusters) in ref. 42 was adapted in refs. 43,44 to study bulk materials irradiated by X-rays. To circumvent the ‘bottleneck’ due to the very high number of active configurations involved after irradiating a material with X-rays, an alternative ‘predominant excitation and relaxation path’ approach was proposed in ref. 43. Although this approach still uses true atomic configurations, it limits their number by restricting the sample relaxation to the predominant paths, as determined by the largest cross sections and transitions rates. The current scheme includes the most probable photoionization and Auger decay channels from each configuration within the path. Consistently, only the predominant collisional ionization processes (from the outermost shell of all atoms and ions considered) and the corresponding three-body recombination rates are included. The collision terms were derived by assuming that isolated atoms interact with the impact particles, and these terms were implemented within the two- and three-body Boltzmann collision integrals (for details, see, for example, refs. 52,53), with respective cross sections and rates of atomic processes induced by X-ray photons obtained with the XATOM code54,55 based on the Hartree–Fock–Slater scheme. Note that the Cu 2p level is degenerate in this framework. It has an energy of 939.11 eV. Therefore, a constant redshift of 6.41 eV was applied to all atomic levels calculated to fit the L3-edge position of neutral copper (932.7 eV). Impact ionization cross sections (and the respective recombination rates) were calculated with Lotz formulas56. The short-range electron–electron scattering was modelled with the Fokker–Planck collision integral53. Pauli blocking was not included, as the electron system was assumed to be classical in this model.