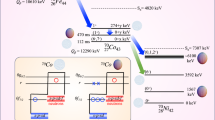
Abstract
In recent decades, rare-isotope facilities have enabled the study of short-lived, neutron-rich nuclei. Their measured properties indicate that shell structure changes in the regime of unbalanced neutron-to-proton ratios compared with that of stable nuclei. In the so-called islands of inversion in the nuclear chart—around the neutron-rich nuclei 32Mg, 42Si and 64Cr, for example—the textbook shell model predicts spherical shapes due to the respective magic neutron numbers of 20, 28 and 40 of these nuclei. However, nuclei in these regions turn out to be deformed in their ground states. Another hallmark of these islands is shape coexistence, where a nucleus assumes different shapes with excitation energy. Here we present evidence for this phenomenon from the observation of an excited 0+ state in 62Cr, two neutrons away from the heart of the island of inversion around neutron number N = 40. We use large-scale shell-model calculations to interpret the results, and we report extrapolations for the doubly magic nucleus 60Ca.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
Data availability
This submission includes as additional supplemental files the relevant data supporting the findings of these studies. Other data are available from the corresponding author upon reasonable request.
Code availability
The techniques developed and exploited in the unpublished computer codes used to generate the results reported in this paper are presented in detail in published works. These works and reasonable requests for clarifications of the techniques or computational methods used are available from the corresponding author.
References
Brown, B. A. The nuclear shell model towards the drip lines. Physics 4, 525–547 (2022).
Nowacki, F., Obertelli, A. & Poves, A. The neutron-rich edge of the nuclear landscape: experiment and theory. Prog. Part. Nucl. Phys. 120, 103866 (2021).
Otsuka, T., Gade, A., Sorlin, O., Suzuki, T. & Utsuno, Y. Evolution of shell structure in exotic nuclei. Rev. Mod. Phys. 92, 015002 (2020).
Sorlin, O. & Porquet, M.-G. Nuclear magic numbers: new features far from stability. Prog. Part. Nucl. Phys. 61, 602–673 (2008).
Rotaru, F. et al. Unveiling the intruder deformed \({0}_{2}^{+}\) state in 34Si. Phys. Rev. Lett. 109, 092503 (2012).
Suchyta, S. et al. Shape coexistence in 68Ni. Phys. Rev. C 89, 021301 (2014).
Mărginean, N. et al. Shape coexistence at zero spin in 64Ni driven by the monopole tensor interaction. Phys. Rev. Lett. 125, 102502 (2020).
Gade, A. & Liddick, S. N. Shape coexistence in neutron-rich nuclei. J. Phys. G: Nucl. Part. Phys. 43, 024001 (2016).
Shimoura, S. et al. Lifetime of the isomeric \({0}_{2}^{+}\) state in 12Be. Phys. Lett. B 654, 87–91 (2007).
Schwerdtfeger, W. et al. Shape coexistence near neutron number N = 20: first identification of the E0 decay from the deformed first excited Jπ = 0+ state in 30Mg. Phys. Rev. Lett. 103, 012501 (2009).
Wimmer, K. et al. Discovery of the shape coexisting 0+ state in 32Mg by a two neutron transfer reaction. Phys. Rev. Lett. 105, 252501 (2010).
Force, C. et al. Prolate-spherical shape coexistence at N = 28 in 44S. Phys. Rev. Lett. 105, 102501 (2010).
Simpson, E. C., Tostevin, J. A., Bazin, D., Brown, B. A. & Gade, A. Two-nucleon knockout spectroscopy at the limits of nuclear stability. Phys. Rev. Lett. 102, 132502 (2009).
Simpson, E. C., Tostevin, J. A., Bazin, D. & Gade, A. Longitudinal momentum distributions of the reaction residues following fast two-nucleon knockout reactions. Phys. Rev. C 79, 064621 (2009).
Simpson, E. C. & Tostevin, J. A. Correlations probed in direct two-nucleon removal reactions. Phys. Rev. C 82, 044616 (2010).
Longfellow, B. et al. Two-neutron knockout as a probe of the composition of states in 22Mg, 23Al, and 24Si. Phys. Rev. C 101, 031303 (2020).
Paschalis, S. et al. The performance of the gamma-ray energy tracking in-beam nuclear array GRETINA. Nucl. Instrum. Methods Phys. Res. Sect. A 709, 44–55 (2013).
Weisshaar, D. et al. The performance of the γ-ray tracking array GRETINA for γ-ray spectroscopy with fast beams of rare isotopes. Nucl. Instrum. Methods Phys. Res. Sect. A 847, 187–198 (2017).
Dao, D. D. & Nowacki, F. Nuclear structure within a discrete nonorthogonal shell model approach: new frontiers. Phys. Rev. C 105, 054314 (2022).
Tarasov, O. B. et al. Discovery of 60Ca and implications for the stability of 70Ca. Phys. Rev. Lett. 121, 022501 (2018).
Lenzi, S. M., Nowacki, F., Poves, A. & Sieja, K. Island of inversion around 64Cr. Phys. Rev. C 82, 054301 (2010).
Magilligan, A., Brown, B. A. & Stroberg, S. R. Data-driven configuration-interaction Hamiltonian extrapolation to 60Ca. Phys. Rev. C 104, L051302 (2021).
Gade, A. et al. Nuclear structure towards N = 40 60Ca: in-beam γ-ray spectroscopy of 58,60Ti. Phys. Rev. Lett. 112, 112503 (2014).
Chen, S. et al. Level structures of 56,58Ca cast doubt on a doubly magic 60Ca. Phys. Lett. B 843, 138025 (2023).
Li, J. Merging of the island of inversion at N = 40 and N = 50. Phys. Lett. B 840, 137893 (2023).
Morrissey, D. J. & Sherrill, B. M. Radioactive nuclear beam facilities based on projectile fragmentation. Philos. Trans. R. Soc. A 356, 1985–2006 (1998).
Portillo, M. et al. Commissioning of the advanced rare isotope separator ARIS at FRIB. Nucl. Instrum. Methods Phys. Res. Sect. B 540, 151–157 (2023).
Bazin, D., Caggiano, J., Sherrill, B., Yurkon, J. & Zeller, A. The S800 spectrograph. Nucl. Instrum. Methods Phys. Res. Sect. B 204, 629–633 (2003).
Gade, A. et al. In-beam γ-ray spectroscopy of 62,64Cr. Phys. Rev. C 103, 014314 (2021).
Bazin, D. et al. New direct reaction: two-proton knockout from neutron-rich nuclei. Phys. Rev. Lett. 91, 012501 (2003).
Tostevin, J. A., Podolyák, G., Brown, B. A. & Hansen, P. G. Correlated two-nucleon stripping reactions. Phys. Rev. C 70, 064602 (2004).
Tostevin, J. A. & Brown, B. A. Diffraction dissociation contributions to two-nucleon knockout reactions and the suppression of shell-model strength. Phys. Rev. C 74, 064604 (2006).
Hansen, P. & Tostevin, J. Direct reactions with exotic nuclei. Annu. Rev. Nucl. Part. Sci. 53, 219–261 (2003).
Rocchini, M. et al. First evidence of axial shape asymmetry and configuration coexistence in 74Zn: suggestion for a northern extension of the N = 40 island of inversion. Phys. Rev. Lett. 130, 122502 (2023).
Zuker, A. P., Poves, A., Nowacki, F. & Lenzi, S. M. Nilsson-SU3 self-consistency in heavy N = Z nuclei. Phys. Rev. C 92, 024320 (2015).
Cortés, M. et al. Shell evolution of N = 40 isotones towards 60Ca: first spectroscopy of 62Ti. Phys. Lett. B 800, 135071 (2020).
Brink, D. & Broglia, R. Nuclear Superfluidity (Cambridge Univ. Press, 2005).
Hagen, G., Hjorth-Jensen, M., Jansen, G. R., Machleidt, R. & Papenbrock, T. Evolution of shell structure in neutron-rich calcium isotopes. Phys. Rev. Lett. 109, 032502 (2012).
Stroberg, S. R. et al. Single-particle structure of silicon isotopes approaching 42Si. Phys. Rev. C 90, 034301 (2014).
Poves, A., Nowacki, F. & Alhassid, Y. Limits on assigning a shape to a nucleus. Phys. Rev. C 101, 054307 (2020).
Caurier, E., Martínez-Pinedo, G., Nowacki, F., Poves, A. & Zuker, A. P. The shell model as a unified view of nuclear structure. Rev. Mod. Phys. 77, 427–488 (2005).
Caurier, E. & Nowacki, F. Present status of shell model techniques. Acta Phys. Pol. B 30, 705–714 (1999).
Arima, A. & Ichimura, M. Quasi-spin formalism and matrix elements in the shell model. Prog. Theor. Phys. 36, 296–312 (1966).
Elliott, J. P. Collective motion in the nuclear shell model. I. Classification schemes for states of mixed configurations. Proc. R. Soc. Lond. A 245, 128–145 (1958).
Arima, A., Harvey, M. & Shimizu, K. Pseudo LS coupling and pseudo SU(3) coupling schemes. Phys. Lett. B 30, 517–522 (1969).
Zuker, A. P., Retamosa, J., Poves, A. & Caurier, E. Spherical shell model description of rotational motion. Phys. Rev. C 52, R1741–R1745 (1995).
Acknowledgements
This material is based upon work supported by the US Department of Energy (DOE), Office of Science, Office of Nuclear Physics and used resources of FRIB Operations, which is a DOE Office of Science User Facility (Award No. DE-SC0023633). Further support by the DOE, Office of Science, Office of Nuclear Physics was provided under Grant Nos. DE-FG02-97ER410541 and DE-SC0023010 (University of North Carolina), DE-FG02-94ER40848 (Triangle Universities Nuclear Laboratory) and DE-AC02-05CH11231 (Lawrence Berkeley National Laboratory) and under Contract DE-AC02-06CH11357 (Argonne National Laboratory) as well as by the Office of High Energy Physics (Grant No. DE-SC0022299, TRAIN-MI). Support was provided by the DOE National Nuclear Security Administration through the Nuclear Science and Security Consortium (Award No. DE-NA0003180). Work at Lawrence Livermore National Laboratory was performed under DOE Contract No. DE-AC52-07NA27344 and was supported by the Lab Directed Research and Development programme (Project No. 23-LW-047). B.P.C. acknowledges support from the National Science Foundation (Grant No. PHY-1848177, CAREER). J.A.T. acknowledges support from the Science and Technology Facilities Council, UK (Grant No. ST/V001108/1). A.P. is supported by Grant No. CEX2020-001007-S funded by MCIN/AEI/10.13039/501100011033 and PID2021-127890NB-I00 (Spain).
Author information
Authors and Affiliations
Contributions
A.G., R.V.F.J. and J.A.T. conceived and led the proposal for the experiment based on discussions with and calculations from F.N., S.M.L. and A.P. C.M.C., S.G., S.N., J.P. and D.W. led the operations of the experimental instruments used. A.G., B.L., R.V.F.J., A.D.A., M.J.B., C.M.C., M.P.C., J.C.-J., H.L.C., B.P.C., P.F., A.M.H., C.P. and E.R. staffed the shifts and monitored the online data quality. A.G. and B.L. led the data analysis. A.G., B.L., R.V.F.J., D.D.D., F.N. and J.A.T. led the interpretation of the data and wrote the first draft. J.A.T., D.D.D., F.N. and A.P. performed the reaction theory and nuclear structure theory calculations.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Anna Corsi, Calvin Johnson and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Quasi- and Pseudo-SU3 plots for the 4p4h configuration in 62Cr.
Left: neutron valence space and single-particle quadrupole moments characterized by the projection of the total angular momentum on the symmetry axis, K. Right: same illustration for protons. The 4p4h configuration corresponds to an axial solution with unique filling of the Nilsson-SU3 levels. The red dots indicate the occupation of the single-particle orbitals with neutrons and protons, respectively.
Extended Data Fig. 2 Quasi- and Pseudo-SU3 plot for the 2p2h configuration in 62Cr.
Left: neutron valence space and single-particle quadrupole moments characterized by the projection of the total angular momentum on the symmetry axis, K. Right: same plot for protons. The 2p2h configuration corresponds to a non-unique Nilsson-SU3 levels filling for the neutron holes and, hence, K mixing and a triaxial shape. The red dots indicate the occupation of the single-particle orbitals with neutrons and protons, respectively.
Supplementary information
Supplementary Data 1
Calibrated, unbinned (1 keV per channel) γ-ray spectrum of Fig. 1 in SpecTcl ASCII format. SpecTcl is publicly available (https://github.com/FRIBDAQ/SpecTcl) and documented.
Supplementary Data 3
Two-dimensional spectrum that correlates the Doppler-reconstructed γ-ray spectrum of 62Cr (4 keV per channel) with the parallel momentum of the 62Cr reaction residues. The first and last channel of the momentum data are −818.946 MeV/c and 797.850 MeV/c, respectively. This matrix was the basis for the measured γ-gated momentum distributions shown in Fig. 3. The matrix is in SpecTcl ASCII format.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Gade, A., Longfellow, B., Janssens, R.V.F. et al. In-beam spectroscopy reveals competing nuclear shapes in the rare isotope 62Cr. Nat. Phys. 21, 37–42 (2025). https://doi.org/10.1038/s41567-024-02680-0
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41567-024-02680-0
This article is cited by
-
Into the islands of inversion
Nature Physics (2025)