Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Signatures of two gaps in the spin susceptibility of a cuprate superconductor

Nature Physics volume 21, pages 97–103 (2025)Cite this article

Subjects

Abstract

A fundamental obstacle to understanding high-temperature superconducting cuprates is that the occurrence of superconductivity hinders the observation of the normal-state properties at low temperature. One important property illustrating this issue is the spin susceptibility: its decrease upon cooling in the normal state is considered as evidence of pseudogap behaviour. However, unambiguous interpretation of this decrease has been impossible, as the crucial low-temperature data inevitably reflect the superconducting pairing rather than the normal state. Here we measure the spin susceptibility of YBa2Cu3Oy at low temperature while suppressing superconductivity in high magnetic field. We found that there are two thermally activated contributions, each of which comes from a different gap, alongside a residual component due to gapless excitations. We relate these two distinct gaps to short-range charge density waves and to the formation of singlets, as occurs in certain quantum spin systems. Both phenomena contribute to the pseudogap at low temperature, supplementing the short-lived antiferromagnetism that initiates pseudogap behaviour at high temperatures. We, therefore, propose that the pseudogap should be regarded as a composite property and that, when not undergoing spin-stripe ordering, underdoped cuprates tend to form short-range spin singlets.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Examples of systems with gaps or pseudogaps in the spin susceptibility.
Fig. 2: Temperature and doping dependence of the spin susceptibility.
Fig. 3: Two-gap phenomenology and phase diagram of underdoped YBa2Cu3Oy.

Similar content being viewed by others

Data availability

Source data are provided with this paper. All other data are available from the corresponding author upon reasonable request.

References

  1. Keimer, B. et al. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).

    ADS  MATH  Google Scholar 

  2. Alloul, H., Ohno, T. & Mendels, P. 89Y NMR evidence for a Fermi-liquid behavior in YBa2Cu3O6+x. Phys. Rev. Lett. 63, 1700–1703 (1989).

    ADS  MATH  Google Scholar 

  3. Johnston, D. C. Magnetic susceptibility scaling in La2−xSrxCuO4−y. Phys. Rev. Lett. 62, 957–960 (1989).

    ADS  MATH  Google Scholar 

  4. Berthier, C. et al. Cross-over temperatures and spin-gap in high Tc cuprate superconductors an NMR approach. Phys. C: Supercond. 282–287, 227–230 (1997).

    ADS  MATH  Google Scholar 

  5. Chen, X., LeBlanc, J. P. F. & Gull, E. Simulation of the NMR response in the pseudogap regime of the cuprates. Nat. Commun. 8, 14986 (2017).

    ADS  MATH  Google Scholar 

  6. Johnston, D. C. in Handbook of Magnetic Materials (ed. Buschow, K. H. J.) Ch. 1, 1–237 (Elsevier, 1997).

  7. Kawasaki, S. et al. Carrier-concentration dependence of the pseudogap ground state of superconducting Bi2Sr2−xLaxCuO6+δ revealed by 63,65Cu-nuclear magnetic resonance in very high magnetic fields. Phys. Rev. Lett. 105, 137002 (2010).

    ADS  MATH  Google Scholar 

  8. Zhou, R. et al. Spin susceptibility across the upper critical field in charge ordered YBa2Cu3Oy. Proc. Natl Acad. Sci. USA 114, 13148–13153 (2017).

    ADS  MATH  Google Scholar 

  9. Wu, T. et al. Magnetic-field-induced charge-stripe order in the high temperature superconductor YBa2Cu3Oy. Nature 477, 191–194 (2011).

    ADS  MATH  Google Scholar 

  10. Gerber, S. et al. Three-dimensional charge density order in YBa2Cu3O6.67 at high magnetic fields. Science 350, 949–952 (2015).

    MATH  Google Scholar 

  11. Wu, T. et al. Emergence of charge order from the vortex state of a high-temperature superconductor. Nat. Commun. 4, 2113 (2013).

    ADS  MATH  Google Scholar 

  12. Tallon, J. L. & Loram, J. W. The doping dependence of T* - what is the real high-Tc phase diagram? Phys. C: Supercond. 349, 53–68 (2001).

    ADS  MATH  Google Scholar 

  13. Blanco-Canosa, S. et al. Resonant X-ray scattering study of charge-density wave correlations in YBa2Cu3O6+x. Phys. Rev. B 90, 054513 (2014).

    ADS  Google Scholar 

  14. Hücker, M. et al. Competing charge, spin, and superconducting orders in underdoped YBa2Cu3Oy. Phys. Rev. B 90, 054514 (2014).

    ADS  MATH  Google Scholar 

  15. Wu, T. et al. Incipient charge order observed by NMR in the normal state of YBa2Cu3Oy. Nat. Commun. 6, 6438 (2015).

    ADS  MATH  Google Scholar 

  16. Borisenko, S. V. et al. Two energy gaps and Fermi-surface ‘arcs’ in NbSe2. Phys. Rev. Lett. 102, 166402 (2009).

    ADS  MATH  Google Scholar 

  17. Parker, C. V. et al. Fluctuating stripes at the onset of the pseudogap in the high-Tc superconductor Bi2Sr2CaCu2O8+x. Nature 468, 677–680 (2010).

    ADS  MATH  Google Scholar 

  18. Comin, R. et al. Charge order driven by Fermi-arc instability in Bi2Sr2−xLaxCuO6+δ. Science 343, 390–392 (2014).

    ADS  MATH  Google Scholar 

  19. Fujita, K. et al. Simultaneous transitions in cuprate momentum-space topology and electronic symmetry breaking. Science 344, 612–616 (2014).

    ADS  MATH  Google Scholar 

  20. Hashimoto, M. et al. Energy gaps in high-transition-temperature cuprate superconductors. Nat. Phys. 10, 483–495 (2014).

    MATH  Google Scholar 

  21. Hinton, J. P. et al. The rate of quasiparticle recombination probes the onset of coherence in cuprate superconductors. Sci. Rep. 6, 23610 (2016).

    ADS  MATH  Google Scholar 

  22. Loret, B. et al. Intimate link between charge density wave, pseudogap and superconducting energy scales in cuprates. Nat. Phys. 15, 771–775 (2019).

    MATH  Google Scholar 

  23. Gruner, T. et al. Charge density wave quantum critical point with strong enhancement of superconductivity. Nat. Phys. 13, 967–972 (2017).

    MATH  Google Scholar 

  24. Ortiz, B. R. et al. Superconductivity in the Z2 kagome metal KV3Sb5. Phys. Rev. Mater. 5, 034801 (2021).

    Google Scholar 

  25. Efetov, K. B., Meier, H. & Pépin, C. Pseudogap state near a quantum critical point. Nat. Phys. 9, 442–446 (2013).

    MATH  Google Scholar 

  26. Hayward, L. E., Hawthorn, D. G., Melko, R. G. & Sachdev, S. Angular fluctuations of a multicomponent order describe the pseudogap of YBa2Cu3O6+x. Science 343, 1336–1339 (2014).

    ADS  Google Scholar 

  27. Fradkin, E., Kivelson, S. A. & Tranquada, J. M. Theory of intertwined orders in high temperature superconductors. Rev. Mod. Phys. 87, 457–482 (2015).

    ADS  Google Scholar 

  28. Emery, V. J., Kivelson, S. A. & Zachar, O. Spin-gap proximity effect mechanism of high-temperature superconductivity. Phys. Rev. B 56, 6120–6147 (1997).

    ADS  MATH  Google Scholar 

  29. Vojta, M. & Sachdev, S. Charge order, superconductivity, and a global phase diagram of doped antiferromagnets. Phys. Rev. Lett. 83, 3916–3919 (1999).

    ADS  MATH  Google Scholar 

  30. Tranquada, J. M. Cuprate superconductors as viewed through a striped lens. Adv. Phys. 69, 437–509 (2020).

    ADS  Google Scholar 

  31. Jiang, H.-C. & Kivelson, S. A. Stripe order enhanced superconductivity in the Hubbard model. Proc. Natl Acad. Sci. USA 119, e2109406119 (2022).

    MATH  Google Scholar 

  32. Dai, Z., Senthil, T. & Lee, P. A. Modeling the pseudogap metallic state in cuprates: quantum disordered pair density wave. Phys. Rev. B 101, 064502 (2020).

    ADS  Google Scholar 

  33. Rossat-Mignod, J. et al. Neutron scattering study of the YBa2Cu3O6+x system. Phys. C: Supercond. 185, 86–92 (1991).

    ADS  Google Scholar 

  34. Haug, D. et al. Neutron scattering study of the magnetic phase diagram of underdoped YBa2Cu3O6+x. New J. Phys. 12, 105006 (2010).

    ADS  MATH  Google Scholar 

  35. Wu, T. et al. Magnetic-field-enhanced spin freezing on the verge of charge ordering in YBa2Cu3O6.45. Phys. Rev. B 88, 014511 (2013).

    ADS  Google Scholar 

  36. Nakano, T. et al. Magnetic properties and electronic conduction of superconducting La2−xSrxCuO4. Phys. Rev. B 49, 16000–16008 (1994).

    ADS  MATH  Google Scholar 

  37. Ning, F. L. et al. Contrasting spin dynamics between underdoped and overdoped Ba(Fe1-xCox)2As2. Phys. Rev. Lett. 104, 037001 (2010).

    ADS  MATH  Google Scholar 

  38. Zhou, R. et al. Quantum criticality in electron-doped BaFe2−xNixAs2. Nat. Commun. 4, 2265 (2013).

    ADS  MATH  Google Scholar 

  39. Adamus, P. et al. Analogies of phonon anomalies and electronic gap features in the infrared response of Sr14−xCaxCu24O41 and underdoped YBa2Cu3O6+x. Rep. Prog. Phys. 86, 044502 (2023).

    ADS  MATH  Google Scholar 

  40. Piskunov, Y. et al. (Sr/Ca)14Cu24O41 spin ladders studied by NMR under pressure. Eur. Phys. J. B: Condens. Matter Complex Syst. 24, 443–456 (2001).

    MATH  Google Scholar 

  41. Vuletić, T. et al. The spin-ladder and spin-chain system (La,Y,Sr,Ca)14Cu24O41: electronic phases, charge and spin dynamics. Phys. Rep. 428, 169–258 (2006).

    ADS  MATH  Google Scholar 

  42. Ohsugi, S. et al. Magnetic order in the hole-doped two-leg ladder compound Sr2.5Ca11.5Cu24O41: evidence from Cu-NMR and -NQR studies on a single crystal. Phys. Rev. Lett. 82, 4715 (1999).

    ADS  MATH  Google Scholar 

  43. Deng, G. et al. Coexistence of long-range magnetic ordering and singlet ground state in the spin-ladder superconductor SrCa13Cu24O41. Phys. Rev. B 88, 174424 (2013).

    ADS  Google Scholar 

  44. Mendels, P. et al. Muon-spin-rotation study of the effect of Zn substitution on magnetism in YBa2Cu3Ox. Phys. Rev. B 49, 10035(R) (1994).

    ADS  MATH  Google Scholar 

  45. Julien, M.-H. et al. 63Cu NMR evidence for enhanced antiferromagnetic correlations around Zn impurities in YBa2Cu3O6.7. Phys. Rev. Lett. 84, 3422–3425 (2000).

    ADS  MATH  Google Scholar 

  46. Suchaneck, A. et al. Incommensurate magnetic order and dynamics induced by spinless impurities in YBa2Cu3O6.6. Phys. Rev. Lett. 105, 037207 (2010).

    ADS  MATH  Google Scholar 

  47. Lee, P. A., Nagaosa, N. & Wen, X.-G. Doping a Mott insulator: physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85 (2006).

    ADS  MATH  Google Scholar 

  48. Carlson, E. W., Orgad, D., Kivelson, S. A. & Emery, V. J. Stripes, electron fractionalization, and ARPES. J. Phys. Chem. Solids 63, 2213–2218 (2002).

    ADS  MATH  Google Scholar 

  49. Walsh, C. et al. Superconductivity in the two-dimensional Hubbard model with cellular dynamical mean-field theory: a quantum impurity model analysis. Phys. Rev. B 108, 075163 (2023).

  50. Yoshinari, Y., Yasuoka, H., Ueda, Y., Koga, K.-i & Kosuge, K. NMR studies of 17O in the normal state of YBa2Cu3O6+x. J. Phys. Soc. Jpn 59, 3698–3711 (1990).

    ADS  MATH  Google Scholar 

  51. Kačmarčík, J. et al. Unusual interplay between superconductivity and field-induced charge order in YBa2Cu3Oy. Phys. Rev. Lett. 121, 167002 (2018).

    ADS  MATH  Google Scholar 

  52. Xiao, B., He, Y.-Y., Georges, A. & Zhang, S. Temperature dependence of spin and charge orders in the doped two-dimensional Hubbard model. Phys. Rev. X 13, 011007 (2023).

    Google Scholar 

  53. Takigawa, M. et al. Cu and O NMR studies of the magnetic properties of YBa2Cu3O6.63 (Tc = 62 K). Phys. Rev. B 43, 247 (1991).

    ADS  MATH  Google Scholar 

  54. Haase, J., Jurkutat, M. & Kohlrautz, J. Contrasting phenomenology of NMR shifts in cuprate superconductors. Condens. Matter 2, 16 (2017).

    Google Scholar 

  55. Ayres, J., Katsnelson, M. I. & Hussey, N. E. Superfluid density and two-component conductivity in hole-doped cuprates. Front. Phys. 10, 1021462 (2022).

    Google Scholar 

  56. Barišić, N. & Sunko, D. K. High-Tc cuprates: a story of two electronic subsystems. J. Supercond. Nov. Magn. 35, 1781–1799 (2022).

    MATH  Google Scholar 

  57. Anderson, P. W. The resonating valence bond state in La2CuO4 and superconductivity. Science 235, 1196–1198 (1987).

    ADS  MATH  Google Scholar 

  58. Punk, M., Allais, A. & Sachdev, S. Quantum dimer model for the pseudogap metal. Proc. Natl Acad. Sci. USA 112, 9552–9557 (2015).

    ADS  MATH  Google Scholar 

  59. Li, H. et al. Low-energy gap emerging from confined nematic states in extremely underdoped cuprate superconductors. npj Quantum Mater. 8, 18 (2023).

    ADS  Google Scholar 

  60. Ye, S. et al. The emergence of global phase coherence from local pairing in underdoped cuprates. Nat. Phys. 19, 1301–1307 (2023).

    MATH  Google Scholar 

  61. Zheng, B.-X. et al. Stripe order in the underdoped region of the two-dimensional Hubbard model. Science 358, 1155–1160 (2017).

    ADS  MathSciNet  MATH  Google Scholar 

  62. Huang, E. W. et al. Numerical evidence of fluctuating stripes in the normal state of high-Tc cuprate superconductors. Science 358, 1161–1164 (2017).

    ADS  MathSciNet  MATH  Google Scholar 

  63. Vinograd, I. et al. Locally commensurate charge-density wave with three-unit-cell periodicity in YBa2Cu3Oy. Nat. Commun. 12, 3274 (2021).

    ADS  MATH  Google Scholar 

  64. Jiang, S., Scalapino, D. J. & White, S. R. Ground-state phase diagram of the t-t'-J model. Proc. Natl Acad. Sci. USA 118, e2109978118 (2021).

    Google Scholar 

  65. Wu, T. et al. 63Cu-NMR study of oxygen disorder in ortho-II YBa2Cu3Oy. Phys. Rev. B 93, 134518 (2016).

    ADS  Google Scholar 

  66. Bankay, M., Mali, M., Roos, J. & Brinkmann, D. Single-spin fluid, spin gap, and d-wave pairing in YBa2Cu4O8: a NMR and NQR study. Phys. Rev. B 50, 6416–6425 (1994).

    ADS  Google Scholar 

  67. Tranquada, J. M. et al. Neutron-scattering study of the dynamical spin susceptibility in YBa2Cu3O6.6. Phys. Rev. B 46, 5561 (1992).

    ADS  MATH  Google Scholar 

  68. Curro, N. J., Imai, T., Slichter, C. P. & Dabrowski, B. High-temperature 63Cu(2) nuclear quadrupole and magnetic resonance measurements of YBa2Cu4O8. Phys. Rev. B 56, 877–885 (1997).

    ADS  Google Scholar 

  69. Ramshaw, B. et al. Vortex lattice melting and Hc2 in underdoped YBa2Cu3Oy. Phys. Rev. B 86, 174501 (2012).

    ADS  MATH  Google Scholar 

  70. Grissonnanche, G. et al. Direct measurement of the upper critical field in cuprate superconductors. Nat. Commun. 5, 3280 (2014).

    ADS  MATH  Google Scholar 

Download references

Acknowledgements

We thank K. Behnia, C. Bernhard, P. Bourges, A. V. Chubukov, A. Georges, S. A. Kivelson, D. LeBoeuf, P. Lee, P. Mendels, D. Orgad, C. Proust, M. Punk, S. Sachdev, A. Sacuto, J. Schmalian, Y. Sidis, J. Tallon, J.M. Tranquada, A.-M. Tremblay, S. R. White and J. Zaanen for discussions. This work was performed at the LNCMI, a member of the European Magnetic Field Laboratory. R.Z., I.V., M.H., T.W., H.M., S.K. and M.-H.J. were supported by the Laboratoire d’Excellence LANEF (Grant No. ANR-10-LABX-51-01) and by the French National Agency for Research (Grant No. ANR-19-CE30-0019, Neptun).

Author information

Author notes

  1. Rui Zhou

    Present address: Institute of Physics, Chinese Academy of Sciences and Beijing National Laboratory for Condensed Matter Physics, Beijing, China

  2. Michihiro Hirata

    Present address: Materials Physics and Applications – Quantum, Los Alamos National Laboratory, Los Alamos, NM, USA

  3. Tao Wu

    Present address: Hefei National Research Center for Physical Sciences at the Microscale, University of Science and Technology of China, Hefei, China

Authors and Affiliations

  1. Laboratoire National des Champs Magnétiques Intenses, CNRS – Université Grenoble Alpes – Université Paul Sabatier – Institut National des Sciences Appliquées – European Magnetic Field Laboratory, Grenoble, France

    Rui Zhou, Igor Vinograd, Michihiro Hirata, Tao Wu, Hadrien Mayaffre, Steffen Krämer & Marc-Henri Julien

  2. Department of Physics and Astronomy, University of British Columbia, Vancouver, British Columbia, Canada

    W. N. Hardy, Ruixing Liang & D. A. Bonn

  3. Canadian Institute for Advanced Research, Toronto, Ontario, Canada

    W. N. Hardy, Ruixing Liang & D. A. Bonn

  4. Max-Planck-Institut für Festkörperforschung, Stuttgart, Germany

    Toshinao Loew, Juan Porras & Bernhard Keimer

Authors
  1. Rui Zhou
    View author publications

    Search author on:PubMed Google Scholar

  2. Igor Vinograd
    View author publications

    Search author on:PubMed Google Scholar

  3. Michihiro Hirata
    View author publications

    Search author on:PubMed Google Scholar

  4. Tao Wu
    View author publications

    Search author on:PubMed Google Scholar

  5. Hadrien Mayaffre
    View author publications

    Search author on:PubMed Google Scholar

  6. Steffen Krämer
    View author publications

    Search author on:PubMed Google Scholar

  7. W. N. Hardy
    View author publications

    Search author on:PubMed Google Scholar

  8. Ruixing Liang
    View author publications

    Search author on:PubMed Google Scholar

  9. D. A. Bonn
    View author publications

    Search author on:PubMed Google Scholar

  10. Toshinao Loew
    View author publications

    Search author on:PubMed Google Scholar

  11. Juan Porras
    View author publications

    Search author on:PubMed Google Scholar

  12. Bernhard Keimer
    View author publications

    Search author on:PubMed Google Scholar

  13. Marc-Henri Julien
    View author publications

    Search author on:PubMed Google Scholar

Contributions

R.Z., I.V., M.H. and T.W. performed the NMR experiments with the help of H.M., S.K. and M.-H.J. R.Z. performed all the data analysis with preliminary input from I.V., M.H. and T.W. and guidance from M.-H.J. W.N.H., R.L., D.A.B., T.L., J.P. and B.K. contributed to the synthesis and the characterization of the samples. M.-H.J. supervised the project and wrote the paper with constant feedback from R.Z. and input from all co-authors.

Corresponding author

Correspondence to Marc-Henri Julien.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Evidence of activated behavior.

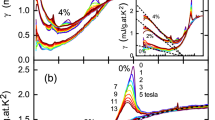
a-f: Knight shift (from which Kres has been subtracted) in vertical logarithmic scale vs. inverse temperature for the different doping levels. The straight line indicates exponential behaviour. g-l: same data vs. temperature. The nonlinear behaviour speaks against a power-law dependence. The p = 0.135 data undulates around the straight line (panel f) because of the larger difficulty in determining the exact line position for this sample: the line shapes are more complex due to ortho-III chain-oxygen order being both more complex and shorter ranged.

Extended Data Fig. 2 Alternative fits.

a–f, Kspin for p = 0.064 (a), p = 0.072 (b), p = 0.090 (c), p = 0.109 (d), p = 0.125 (e) and p = 0.135 (f) (same data as in Fig. 2). The solid lines are fits with the two-gap function Kspin = Kres + KL (1-tanh2(ΔL/2kBT)) + KH (1-tanh2(ΔH/2kBT)). Fit results are shown in Extended Data Fig. 3. Error bars represent the added uncertainties in the line positions, in the field reference and in the 2nd-order quadrupole shift correction, all calculated from one standard deviation in the Gaussian peak fits of the relevant NMR lines.

Extended Data Fig. 3 Comparison of results for two different fitting functions.

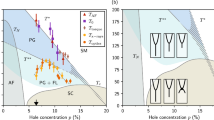
(a) Onset temperature TCDW of short-range 2D CDW, from refs. 13,14,15. The thick trace is a parabolic function that represents the p dependence of TCDW and its experimental uncertainty. (b) Low-gap values ΔL extracted from the two different fits, and using one or two gap functions (see text), compared to the same parabola as in (a). (c–f) Other fit parameters. Error bars for ΔH, ΔL, KH, KL and Kres represent one standard deviation in the fit results.

Extended Data Fig. 4 89Y NMR evidence of spin freezing for p = 0.064 (YBa2Cu3O6.38).

A broad peak in the spin-lattice relaxation rate 1/T1 vs. T is the typical signature of spin fluctuations becoming as slow as the NMR frequency scale of 31 MHz (here in a field of 15 T). Error bars correspond to one standard deviation in fits of the time-dependence of the NMR signal to the theoretical law for relaxation by magnetic fluctuations. The line is a guide to the eye.

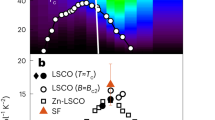
Extended Data Fig. 5 Comparison of the spin susceptibility of LSCO and YBCO.

Bulk magnetization data for La1.86Sr0.14CuO4 is from Nakano et al.36. 63Cu Knight shift data for YBa2Cu4O8 is from Curro et al.68. Unlike YBa2Cu3Oy, for which chain-oxygen atoms become mobile above room temperature, stoichiometric YBa2Cu4O8 does not suffer this problem. This allows one to see that the broad susceptibility maximum, inherited from the behaviour of the undoped square lattice, is present in the YBCO system as well.

Extended Data Fig. 6 Predicting Kres for YBa2Cu3O6.43.

The data at B = 15 T (measured with B | |c) and at 30 T (measured with B tilted by 16° off the c axis) correspond to the zero-temperature extrapolation of our K(T) measurements of O(2) sites at low T. The value at B = 0 is the zero-temperature extrapolation of our K(T) measurements of O(2) sites at low T, with B ⊥ c and B = 9 T « \({B}_{{\rm{c}}2}^{\perp }\). The thick blue line represents the expected B dependence on the basis of results at other doping levels8: linear increase up to Bc2(T = 0) = 45 T (value taken from an interpolation of the results in refs. 69,70) and saturation above Bc2. The value K(T = 0, B = Bc2) = Kres is predicted to be equal to about 0.036%. Within error bars, this agrees well with the fit result in Fig. 2b: Kres(fit) = 0.039 ± 0.01%. Error bars represent the added uncertainties in the line positions, in the field reference and in the 2nd-order quadrupole shift correction, all calculated from one standard deviation in the Gaussian peak fits of the relevant NMR lines.

Extended Data Fig. 7 Absence of direct correlation between residual spin susceptibility and disorder.

The linewidth values correspond to the width of the 17O(2) central line at room temperature. For p = 0.064, we used the ratio of 89Y NMR linewidth between p = 0.064 and p = 0.072 samples. While Kres=Kspin(T = 0) is nearly identical for p = 0.109 and p = 0.090, disorder (as quantified by the NMR line width) differs by a factor of five. p = 0.135 also has identical Kres, yet its linewidth is larger than p = 0.109 by a factor 2.3. Therefore, although both χres and disorder tend to increase at low doping, this likely occurs for different reasons: weakening of CDW correlations for the former, increased oxygen disorder for the latter (notice that the weakening of CDW correlations may, or may not, be partially caused by the increased disorder at low p). Error bars for Kres represent one standard deviation in the fit results. Lines are guides to the eye.

Extended Data Fig. 8 Determining the oxygen concentration with chain-Cu NMR.

63Cu(1E) (empty-chain site) low-frequency quadrupole satellites of the 63Cu NMR spectrum. The labels iV (i = 0, 1, 2, 3) indicate Cu(1E) sites having a number i of nearest-neighbor vacancies. Each line is fitted with a Gaussian function and the relative integrated intensities of the Cu(1E)0V and Cu(1E)1V sites are used to determine the actual oxygen concentration y (see ref. 65 for details about the method).

Extended Data Fig. 9 Orbital contribution to the 17O Knight shift (O(2) sites, B | |b).

The values (red dots) are obtained from the scaling of O(2) and O(3) Knight shifts (Supplementary Information). The data is shown in the same vertical scale as Fig. 2, in order to facilitate comparison. Clearly, Korb « Kspin at any T and can therefore be neglected. Error bars represent the estimated uncertainty in the scaling between O(2) and O(3) Knight shifts.

Extended Data Table 1 Sample properties
Full size table

Supplementary information

Supplementary Information

Two figures with additional Knight shift data.

Source data

Source Data Fig. 2

Knight data for all samples in Fig. 2a–f.

Source Data Fig. 3

Fitting parameters in Fig. 3a–d.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, R., Vinograd, I., Hirata, M. et al. Signatures of two gaps in the spin susceptibility of a cuprate superconductor. Nat. Phys. 21, 97–103 (2025). https://doi.org/10.1038/s41567-024-02692-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-024-02692-w

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing