Abstract
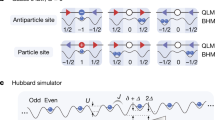
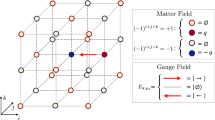
The topological θ-angle is central to several gauge theories in condensed-matter and high-energy physics. For example, it is responsible for the strong CP problem in quantum chromodynamics and can emerge in effective theories of electrodynamics in topological insulators. Although analogue quantum simulators potentially offer a venue for realizing and controlling the θ-angle, doing so has hitherto remained an outstanding challenge. Here, we describe the experimental realization of a tunable topological θ-angle in a Bose–Hubbard gauge-theory quantum simulator, which was implemented through a tilted superlattice potential that induces an effective background electric field. We demonstrate the emerging physics through the direct observation of the confinement–deconfinement transition of (1 + 1)-dimensional quantum electrodynamics. Using an atomic-precision quantum gas microscope, we distinguish between the confined and deconfined phases by monitoring the real-time evolution of particle–antiparticle pairs. Our work provides a step forward in the realization of topological terms on modern quantum simulators.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Source data are provided within this paper. The data for the figures that support the findings of this study are also available from Zenodo at https://doi.org/10.5281/zenodo.13733573 (ref. 52).
References
Weinberg, S. The Quantum Theory of Fields, Vol. 2 (Cambridge Univ. Press, 1995).
Jackiw, R. & Rebbi, C. Vacuum periodicity in a Yang-Mills quantum theory. Phys. Rev. Lett. 37, 172–175 (1976).
Callan, C., Dashen, R. & Gross, D. The structure of the gauge theory vacuum. Phys. Lett. B 63, 334–340 (1976).
’t Hooft, G. Computation of the quantum effects due to a four-dimensional pseudoparticle. Phys. Rev. D 14, 3432–3450 (1976).
Mannel, T. Theory and phenomenology of CP violation. Nucl. Phys. B Proc. Suppl. 167, 115–119 (2007).
Buyens, B., Haegeman, J., Verschelde, H., Verstraete, F. & Van Acoleyen, K. Confinement and string breaking for QED2 in the Hamiltonian picture. Phys. Rev. X 6, 041040 (2016).
Surace, F. M. et al. Lattice gauge theories and string dynamics in Rydberg atom quantum simulators. Phys. Rev. X 10, 021041 (2020).
Li, R., Wang, J., Qi, X.-L. & Zhang, S.-C. Dynamical axion field in topological magnetic insulators. Nat. Phys. 6, 284–288 (2010).
Haldane, F. D. M. Continuum dynamics of the 1-D Heisenberg antiferromagnet: identification with the O(3) nonlinear sigma model. Phys. Lett. A 93, 464–468 (1983).
Haldane, F. D. M. Nonlinear field theory of large-spin Heisenberg antiferromagnets: semiclassically quantized solitons of the one-dimensional easy-axis Néel state. Phys. Rev. Lett. 50, 1153–1156 (1983).
Dalmonte, M. & Montangero, S. Lattice gauge theory simulations in the quantum information era. Contemp. Phys. 57, 388–412 (2016).
Zohar, E., Cirac, J. I. & Reznik, B. Quantum simulations of lattice gauge theories using ultracold atoms in optical lattices. Rep. Prog. Phys. 79, 014401 (2015).
Bañuls, M. C. et al. Simulating lattice gauge theories within quantum technologies. Eur. Phys. J. D 74, 165 (2020).
Aidelsburger, M. et al. Cold atoms meet lattice gauge theory. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 380, 20210064 (2022).
Zohar, E. Quantum simulation of lattice gauge theories in more than one space dimension—requirements, challenges and methods. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 380, 20210069 (2022).
Halimeh, J. C. & Hauke, P. Reliability of lattice gauge theories. Phys. Rev. Lett. 125, 030503 (2020).
Martinez, E. A. et al. Real-time dynamics of lattice gauge theories with a few-qubit quantum computer. Nature 534, 516–519 (2016).
Schweizer, C. et al. Floquet approach to \({{\mathbb{Z}}}_{2}\) lattice gauge theories with ultracold atoms in optical lattices. Nat. Phys. 15, 1168–1173 (2019).
Görg, F. et al. Realization of density-dependent Peierls phases to engineer quantized gauge fields coupled to ultracold matter. Nat. Phys. 15, 1161–1167 (2019).
Mil, A. et al. A scalable realization of local U(1) gauge invariance in cold atomic mixtures. Science 367, 1128–1130 (2020).
Yang, B. et al. Observation of gauge invariance in a 71-site Bose–Hubbard quantum simulator. Nature 587, 392–396 (2020).
Zhou, Z.-Y. et al. Thermalization dynamics of a gauge theory on a quantum simulator. Science 377, 311–314 (2022).
Nguyen, N. H. et al. Digital quantum simulation of the Schwinger model and symmetry protection with trapped ions. PRX Quantum 3, 020324 (2022).
Wang, Z. et al. Observation of emergent \({{\mathbb{Z}}}_{2}\) gauge invariance in a superconducting circuit. Phys. Rev. Res. 4, L022060 (2022).
Mildenberger, J., Mruczkiewicz, W., Halimeh, J. C., Jiang, Z. & Hauke, P. Probing confinement in a \({{\mathbb{Z}}}_{2}\) lattice gauge theory on a quantum computer. Preprint at arxiv.org/abs/2203.08905 (2022).
Chandrasekharan, S. & Wiese, U.-J. Quantum link models: a discrete approach to gauge theories. Nucl. Phys. B 492, 455 – 471 (1997).
Halimeh, J. C., McCulloch, I. P., Yang, B. & Hauke, P. Tuning the topological θ-angle in cold-atom quantum simulators of gauge theories. PRX Quantum 3, 040316 (2022).
Cheng, Y., Liu, S., Zheng, W., Zhang, P. & Zhai, H. Tunable confinement-deconfinement transition in an ultracold-atom quantum simulator. PRX Quantum 3, 040317 (2022).
Jaksch, D., Bruder, C., Cirac, J. I., Gardiner, C. W. & Zoller, P. Cold bosonic atoms in optical lattices. Phys. Rev. Lett. 81, 3108–3111 (1998).
Greiner, M., Mandel, O., Esslinger, T., Hänsch, T. W. & Bloch, I. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 415, 39–44 (2002).
Sachdev, S., Sengupta, K. & Girvin, S. Mott insulators in strong electric fields. Phys. Rev. B 66, 075128 (2002).
Simon, J. et al. Quantum simulation of antiferromagnetic spin chains in an optical lattice. Nature 472, 307–312 (2011).
Su, G.-X. et al. Observation of many-body scarring in a Bose–Hubbard quantum simulator. Phys. Rev. Res. 5, 023010 (2023).
Zhang, W.-Y. et al. Scalable multipartite entanglement created by spin exchange in an optical lattice. Phys. Rev. Lett. 131, 073401 (2023).
Zohar, E. & Cirac, J. I. Removing staggered fermionic matter in U(N) and SU(N) lattice gauge theories. Phys. Rev. D 99, 114511 (2019).
Coleman, S. More about the massive Schwinger model. Ann. Phys. 101, 239–267 (1976).
Desaules, J.-Y. et al. Ergodicity breaking under confinement in cold-atom quantum simulators. Quantum 8, 1274 (2024).
Wang, H.-Y. et al. Interrelated thermalization and quantum criticality in a lattice gauge simulator. Phys. Rev. Lett. 131, 050401 (2023).
Banerjee, D. et al. Atomic quantum simulation of dynamical gauge fields coupled to fermionic matter: from string breaking to evolution after a quench. Phys. Rev. Lett. 109, 175302 (2012).
Lagnese, G., Surace, F. M., Kormos, M. & Calabrese, P. False vacuum decay in quantum spin chains. Phys. Rev. B 104, L201106 (2021).
Berges, J., Heller, M. P., Mazeliauskas, A. & Venugopalan, R. QCD thermalization: ab initio approaches and interdisciplinary connections. Rev. Mod. Phys. 93, 035003 (2021).
Zache, T. V. et al. Dynamical topological transitions in the massive Schwinger model with a θ term. Phys. Rev. Lett. 122, 050403 (2019).
Huang, Y.-P., Banerjee, D. & Heyl, M. Dynamical quantum phase transitions in U(1) quantum link models. Phys. Rev. Lett. 122, 250401 (2019).
Smith, A., Knolle, J., Kovrizhin, D. L. & Moessner, R. Disorder-free localization. Phys. Rev. Lett. 118, 266601 (2017).
Brenes, M., Dalmonte, M., Heyl, M. & Scardicchio, A. Many-body localization dynamics from gauge invariance. Phys. Rev. Lett. 120, 030601 (2018).
Osborne, J., Yang, B., McCulloch, I. P., Hauke, P. & Halimeh, J. C. Spin-S U(1) quantum link models with dynamical matter on a quantum simulator. Preprint at arxiv.org/abs/2305.06368 (2023).
Osborne, J., McCulloch, I. P., Yang, B., Hauke, P. & Halimeh, J. C. Large-scale 2 + 1D U(1) gauge theory with dynamical matter in a cold-atom quantum simulator. Preprint at arxiv.org/abs/2211.01380 (2022).
Schwinger, J. On gauge invariance and vacuum polarization. Phys. Rev. 82, 664–679 (1951).
Kogut, J. B. An introduction to lattice gauge theory and spin systems. Rev. Mod. Phys. 51, 659–713 (1979).
Hauke, P., Marcos, D., Dalmonte, M. & Zoller, P. Quantum simulation of a lattice Schwinger model in a chain of trapped ions. Phys. Rev. X 3, 041018 (2013).
Sidje, R. B. Expokit: a software package for computing matrix exponentials. ACM Trans. Math. Softw. 24, 130–156 (1998).
Zhang, W.-Y. et al. Data for ‘Observation of microscopic confinement dynamics by a tunable topological θ-angle’. Zenodo. https://doi.org/10.5281/zenodo.13733573 (2024).
Acknowledgements
We thank H. Zhai for discussions. This work was supported by the NNSFC (Grant No. 12125409), the Innovation Programme for Quantum Science and Technology (Grant No. 2021ZD0302000) and an Anhui Provincial Major Science and Technology Project (Grant No. 202103a13010005). W.-Y.Z. acknowledges support from the Postdoctoral Fellowship Programme of CPSF (Grant No. GZC20241659). Y.C. acknowledges support from the NSFC (Grant Nos. 12204034 and 12374251) and Fundamental Research Funds for the Central Universities (Grant No. FRFTP-22-101A1). J.C.H. acknowledges funding by the Max Planck Society, the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2111 – 390814868, and the European Research Council (ERC) under the European Union’s Horizon Europe research and innovation program (Grant Agreement No. 101165667)—ERC Starting Grant QuSiGauge. B.Y. acknowledges the National Key R&D Programme of China (Grant No. 2022YFA1405800), the NNSFC (Grant No. 12274199) and a Guangdong Major Project of Basic and Applied Basic Research (Grant No. 2023B0303000011). W.Z. acknowledges support from the NSFC (Grant Nos. GG2030007011 and GG2030040453) and the Innovation Programme for Quantum Science and Technology (Grant No. 2021ZD0302004). P.H. acknowledges funding from the European Union through the HE research and innovation programme (Grant No. GA 101080086 NeQST) and the Next Generation EU, Mission 4 Component 2 (Grant No. CUP E53D23002240006), from the Italian Ministry of University and Research through Project FARE DAVNE (G R20PEX7Y3A) and Project DYNAMITE QUANTERA2_00056 ERANET, which were co-funded by the European Union H2020 (GA 101017733) and from the ICSC – Centro Nazionale di Ricerca in HPC, Big Data and Quantum Computing, the Provincia Autonoma di Trento and Q@TN. The views and opinions expressed are those of the authors only and do not necessarily reflect those of the granting authorities.
Author information
Authors and Affiliations
Contributions
Y.C., P.H., J.C.H., Z.-S.Y. and J.-W.P. conceived the research. Y.C., B.Y., P.H., W.Z. and J.C.H. developed the theory. W.-Y.Z., Z.-S.Y. and J.-W.P. designed the experiment. W.-Y.Z., Y.L., M.-G.H., H.-Y.W., T.-Y.W., Z.-H.Z., G.-X.S., Z.-Y.Z., Y.-G.Z. and H.S. conducted the experiments and collected the data. W.-Y.Z., Y.L. and Y.C. contributed to the data analysis. All authors contributed to writing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Overlaps between the target states and the deterministic configurations.
The numerical overlaps between the low-energy excited state \(\left\vert {\psi }_{t}\right\rangle\) and two deterministic states, namely \(\left\vert {\psi }_{d}\right\rangle =\left\vert 2020112020\right\rangle\) and \(\left\vert 1111201111\right\rangle\), are shown as solid blue and orange lines, respectively, for different values of \(\frac{m}{\kappa }\).
Extended Data Fig. 2 Procedures of initial state preparation in the positive mass region.
a. An illustration of the atom distribution of the prepared unity-filled Mott insulator state after staggered immersion cooling. Atoms in orange-shaded chains are then addressed by DMD light. b. An illustration of the atomic spin distribution after the site-dependent addressing. c. An illustration of the state after we merge every two atoms in \(\left\vert \downarrow \right\rangle\) state onto a single site along the y direction. d. The prepared copies of \(\left\vert 2020112020\right\rangle\) state along the y direction.
Extended Data Fig. 3 Procedures of initial state preparation in the negative mass region.
a. An illustration of the atom distribution of the prepared unity-filled Mott insulator state after staggered immersion cooling. Atoms in orange-shaded chains are then addressed by DMD light. b. An illustration of the atomic spin distribution after the site-dependent addressing. c. An illustration of the state after we adiabatically transfer every two atoms in the \(\left\vert \downarrow \right\rangle\) state onto a single site along the y direction. d. The prepared copies of \(\left\vert 1111201111\right\rangle\) state along the y direction.
Extended Data Fig. 4 Adiabatic passage.
a. Schematic total optical lattice potentials for the \(\left\vert \downarrow \right\rangle\) (solid blue line) atoms together with the relevant state-independent staggered potential δ and state-dependent tilt gradient Δ before and after the adiabatic passage process. Solid blue circles indicate an exemplary initial state of \(\left\vert \downarrow \right\rangle\) atoms in the optical lattice. The initial atom distribution \(\left\vert \downarrow ,\downarrow ,\downarrow ,\downarrow ,\downarrow ,\downarrow \right\rangle\) is transferred into \(\left\vert \downarrow \downarrow ,0,\downarrow \downarrow ,0,\downarrow \downarrow ,0\right\rangle\). b. The corresponding ramping protocols are employed in the adiabatic passage process. c. Schematic total optical lattice potentials for the \(\left\vert \downarrow \right\rangle\) (solid blue line) and \(\left\vert \uparrow \right\rangle\) atoms (solid orange line) together with the relevant state-independent staggered potential δ and state-dependent tilt gradient (Δ for \(\left\vert \downarrow \right\rangle\) atoms, and − 2Δ for \(\left\vert \uparrow \right\rangle\) atoms) before and after the adiabatic passage process. Solid circles indicate an exemplary initial state of \(\left\vert \downarrow \right\rangle\) (blue circles) and \(\left\vert \uparrow \right\rangle\) atoms (orange circles) in the optical lattice. The initial atom distribution \(\left\vert \downarrow ,\uparrow ,\downarrow ,\uparrow ,\downarrow ,\uparrow \right\rangle\) is kept unchanged. d. Numerical results of the time-resolved density profiles for \(\left\vert \uparrow \right\rangle\) state (left) and \(\left\vert \downarrow \right\rangle\) state (right), respectively. e. Probabilities of the atom distributions of \(\left\vert \downarrow ,\downarrow ,\downarrow ,\downarrow ,\downarrow ,\downarrow \right\rangle\) and \(\left\vert \downarrow \downarrow ,0,\downarrow \downarrow ,0,\downarrow \downarrow ,0\right\rangle\) during the adiabatic passage process. f. Numerical results of the time-resolved density profiles for \(\left\vert \uparrow \right\rangle\) state (left) and \(\left\vert \downarrow \right\rangle\) state (right), respectively. g. Probabilities of the atom distribution of \(\left\vert \downarrow ,\uparrow ,\downarrow ,\uparrow ,\downarrow ,\uparrow \right\rangle\) during the adiabatic passage process.
Extended Data Fig. 5 Numerical results in the positive mass region.
a. The time-resolved density profiles and two-point correlations at various χ/κ. The extracted time-resolved results of the observables b \({\mathcal{E}}(t)\), c \({\mathcal{M}}(t)\), and d \({\mathcal{E}}(t)/{\mathcal{M}}(t)\), at various χ/κ.
Extended Data Fig. 6 Numerical results in the negative mass region.
a. The time-resolved density profiles. b. The time-resolved two-point correlations. The extracted time-resolved results of the observables c \({\mathcal{E}}(t)\), d \({\mathcal{M}}(t)\), and e \({\mathcal{E}}(t)/{\mathcal{M}}(t)\).
Extended Data Fig. 7 Influence of disorder.
a. Numerical simulation results in the presence of disorders of different amplitudes d. b. The dark blue solid dots are the experimental results under χ = 0. The light blue solid dots are the experimental results under \(\frac{\chi }{\kappa }=0.1\). The dark-shaded region represents the numerical sampling result under χ = 0 with uniformly distributed random disorders in the interval (0, d = 0.24κ). The light-shaded region represents the numerical sampling result under \(\frac{\chi }{\kappa }=0.1\) with uniformly distributed random disorders in the interval (0, d = 0.24κ).
Source data
Source Data Fig. 1
Figure 1 is a schematic illustration of the principle without a corresponding raw data counterpart.
Source Data Fig. 2
Statistical source data.
Source Data Fig. 3
Statistical source data.
Source Data Fig. 4
Statistical source data.
Source Data Extended Data Fig. 1
Statistical source data.
Source Data Extended Data Fig. 4
Statistical source data.
Source Data Extended Data Fig. 5
Statistical source data.
Source Data Extended Data Fig. 6
Statistical source data.
Source Data Extended Data Fig. 7
Statistical source data.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zhang, WY., Liu, Y., Cheng, Y. et al. Observation of microscopic confinement dynamics by a tunable topological θ-angle. Nat. Phys. 21, 155–160 (2025). https://doi.org/10.1038/s41567-024-02702-x
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41567-024-02702-x
This article is cited by
-
Suppressing nonperturbative gauge errors in the thermodynamic limit using local pseudogenerators
Communications Physics (2025)
-
Protecting gauge symmetries in the dynamics of SU(3) lattice gauge theories
Communications Physics (2025)
-
Cold-atom quantum simulators of gauge theories
Nature Physics (2025)
-
Dynamical Aharonov-Bohm cages and tight meson confinement in a \({{\mathbb{Z}}}_{2}\)-loop gauge theory
Communications Physics (2025)
-
First-order phase transition of the Schwinger model with a quantum computer
npj Quantum Information (2025)