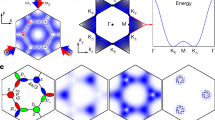
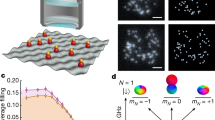
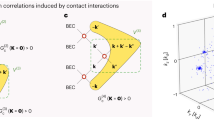
Abstract
Counterflow superfluidity is an anomalous quantum phase that was predicted two decades ago in the context of a two-component Bose–Hubbard model. In this phase, although both components exhibit fluidity, their correlated counterflow currents cancel each other out, resulting in the system behaving as an incompressible Mott insulator. However, realizing and identifying this phase experimentally has proven challenging due to the stringent requirements for a single set-up, including defect-free state preparation, minimal heating during coherent manipulations, and spin- and site-resolved detection of the phases. Here, we report on the observation of counterflow superfluidity in a binary Bose mixture in optical lattices. After preparing a low-entropy spin-Mott state by conveying two spin-1/2 bosonic atoms at every single lattice site to form a doublon, we adiabatically drove the system to the counterflow superfluid phase at approximately 1 nK. We observed features of antipair correlations through site- and spin-resolved quantum-gas microscopy in both real and momentum spaces. Finally, we measured long-range off-diagonal spin correlations in the rotated basis, revealing a correlation length approaching the system size. These techniques and observations demonstrated here provide accessibility to Borromean counterfluids.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All the data are available from the corresponding authors upon reasonable request. Source data are provided with this paper. The data are also available via figshare at https://doi.org/10.6084/m9.figshare.27084313 (ref. 64).
References
Feynman, R. P. Superfluidity and superconductivity. Rev. Mod. Phys. 29, 205–212 (1957).
Yang, C.-N. Concept of off-diagonal long-range order and the quantum phases of liquid He and of superconductors. Rev. Mod. Phys. 34, 694–704 (1962).
Leggett, A. Superfluidity. Rev. Mod. Phys. 71, S318–S323 (1999).
Kapitza, P. Viscosity of liquid helium below the λ-point. Nature 141, 74 (1938).
Allen, J. & Misener, A. Flow phenomena in liquid helium ii. Nature 142, 643–644 (1938).
Bardeen, J., Cooper, L. N. & Schrieffer, J. R. Microscopic theory of superconductivity. Phys. Rev. 106, 162–164 (1957).
Osheroff, D. D., Richardson, R. C. & Lee, D. M. Evidence for a new phase of solid He3. Phys. Rev. Lett. 28, 885–888 (1972).
Anderson, M. H., Ensher, J. R., Matthews, M. R., Wieman, C. E. & Cornell, E. A. Observation of Bose-Einstein condensation in a dilute atomic vapor. Science 269, 198–201 (1995).
Davis, K. B. et al. Bose-Einstein condensation in a gas of sodium atoms. Phys. Rev. Lett. 75, 3969–3973 (1995).
Regal, C. A., Greiner, M. & Jin, D. S. Observation of resonance condensation of fermionic atom pairs. Phys. Rev. Lett. 92, 040403 (2004).
Greiner, M., Mandel, O., Esslinger, T., Hänsch, T. W. & Bloch, I. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 415, 39–44 (2002).
Kuklov, A. & Svistunov, B. Counterflow superfluidity of two-species ultracold atoms in a commensurate optical lattice. Phys. Rev. Lett. 90, 100401 (2003).
Altman, E., Hofstetter, W., Demler, E. & Lukin, M. D. Phase diagram of two-component bosons on an optical lattice. New J. Phys. https://doi.org/10.1088/1367-2630/5/1/113 (2003).
Kuklov, A., Prokof’ev, N. & Svistunov, B. Superfluid-superfluid phase transitions in a two-component Bose-Einstein condensate. Phys. Rev. Lett. 92, 030403 (2004).
Duan, L. M., Demler, E. & Lukin, M. D. Controlling spin exchange interactions of ultracold atoms in optical lattices. Phys. Rev. Lett. 91, 090402 (2003).
Hubener, A., Snoek, M. & Hofstetter, W. Magnetic phases of two-component ultracold bosons in an optical lattice. Phys. Rev. B 80, 245109 (2009).
Powell, S. Magnetic phases and transitions of the two-species Bose-Hubbard model. Phys. Rev. A 79, 053614 (2009).
Schachenmayer, J. et al. Adiabatic cooling of bosons in lattices to magnetically ordered quantum states. Phys. Rev. A 92, 041602 (2015).
de Forges de Parny, L. & Rousseau, V. Magnetic phase transition in the ground-state phase diagram of binary Bose gases in optical lattices. Europhys. Lett. 134, 16001 (2021).
Basak, S. & Pu, H. Strongly interacting two-component coupled Bose gas in optical lattices. Phys. Rev. A 104, 053326 (2021).
Hu, A. et al. Counterflow and paired superfluidity in one-dimensional Bose mixtures in optical lattices. Phys. Rev. A 80, 023619 (2009).
Menotti, C. & Stringari, S. Detection of pair-superfluidity for bosonic mixtures in optical lattices. Phys. Rev. A 81, 045604 (2010).
Hu, A. et al. Detecting paired and counterflow superfluidity via dipole oscillations. Phys. Rev. A 84, 041609 (2011).
Venegas-Gomez, A. et al. Adiabatic preparation of entangled, magnetically ordered states with cold bosons in optical lattices. Quantum Sci. Technol. 5, 045013 (2020).
Venegas-Gomez, A., Buyskikh, A. S., Schachenmayer, J., Ketterle, W. & Daley, A. J. Dynamics of rotated spin states and magnetic ordering with two-component bosonic atoms in optical lattices. Phys. Rev. A 102, 023321 (2020).
Colussi, V. E., Caleffi, F., Menotti, C. & Recati, A. Quantum Gutzwiller approach for the two-component Bose-Hubbard model. SciPost Phys. https://doi.org/10.21468/SciPostPhys.12.3.111 (2022).
Chung, W. et al. Tunable single-ion anisotropy in spin-1 models realized with ultracold atoms. Phys. Rev. Lett. 126, 163203 (2021).
De Hond, J. et al. Preparation of the spin-Mott state: a spinful Mott insulator of repulsively bound pairs. Phys. Rev. Lett. 128, 93401 (2022).
Dimitrova, I. et al. Many-body spin rotation by adiabatic passage in spin-1/2 XXZ chains of ultracold atoms. Quantum Sci. Technol. 8, 035018 (2023).
Yang, B. et al. Cooling and entangling ultracold atoms in optical lattices. Science 369, 550–553 (2020).
Zheng, Y.-G. et al. Robust site-resolved addressing via dynamically tracking the phase of optical lattices. Opt. Lett. 47, 4239 (2022).
Prüfer, M. et al. Condensation and thermalization of an easy-plane ferromagnet in a spinor Bose gas. Nat. Phys. 18, 1459–1463 (2022).
Chen, C. et al. Continuous symmetry breaking in a two-dimensional Rydberg array. Nature 616, 691–695 (2023).
Feng, L. et al. Continuous symmetry breaking in a trapped-ion spin chain. Nature 623, 713–717 (2023).
Bloch, I., Dalibard, J. & Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885–964 (2008).
Fölling, S. et al. Spatial quantum noise interferometry in expanding ultracold atom clouds. Nature 434, 481–484 (2005).
Simon, J. et al. Quantum simulation of antiferromagnetic spin chains in an optical lattice. Nature 472, 307–312 (2011).
Yang, B. et al. Observation of gauge invariance in a 71-site Bose-Hubbard quantum simulator. Nature 587, 392–396 (2020).
Rosenberg, J. S., Christakis, L., Guardado-Sanchez, E., Yan, Z. Z. & Bakr, W. S. Observation of the Hanbury Brown and Twiss effect with ultracold molecules. Nat. Phys. 18, 1062–1066 (2022).
Zheng, Y.-G. et al. Efficiently extracting multi-point correlations of a Floquet thermalized system. Preprint at https://arxiv.org/abs/2210.08556 (2022).
Hanbury Brown, B. & Twiss, R. Q. Correlation between photons in two coherent beams of light. Nature 177, 27–29 (1956).
Mandel, O. et al. Controlled collisions for multi-particle entanglement of optically trapped atoms. Nature 425, 937–940 (2003).
Dai, H. N. et al. Generation and detection of atomic spin entanglement in optical lattices. Nat. Phys. 12, 783–787 (2016).
Zhang, W.-Y. et al. Scalable multipartite entanglement created by spin exchange in an optical lattice. Phys. Rev. Lett. 131, 073401 (2023).
Boothroyd, A. T. Principles of Neutron Scattering from Condensed Matter (Oxford Academic, 2020).
Zheng, Z., Pu, H., Zou, X. & Guo, G. Artificial topological models based on a one-dimensional spin-dependent optical lattice. Phys. Rev. A 95, 013616 (2017).
Chen, X., Gu, Z.-C., Liu, Z.-X. & Wen, X.-G. Symmetry-protected topological orders in interacting bosonic systems. Science 338, 1604–1606 (2012).
Sun, H. et al. Realization of a bosonic antiferromagnet. Nat. Phys. 17, 990–994 (2021).
Haldane, F. D. M. Nonlinear field theory of large-spin Heisenberg antiferromagnets: semiclassically quantized solitons of the one-dimensional easy-axis Néel state. Phys. Rev. Lett. 50, 1153–1156 (1983).
Yang, H., Li, L., Okunishi, K. & Katsura, H. Duality, criticality, anomaly, and topology in quantum spin-1 chains. Phys. Rev. B 107, 125158 (2023).
Radzihovsky, L. Pseudospin canting transition and stripes in bilayer quantum Hall ferromagnets: a self-charging capacitor. Phys. Rev. Lett. 87, 236802 (2001).
Blomquist, E., Syrwid, A. & Babaev, E. Borromean supercounterfluidity. Phys. Rev. Lett. 127, 255303 (2021).
Babaev, E. & Svistunov, B. Hydrodynamics of Borromean counterfluids. Phys. Rev. Lett. 133, 026001 (2024).
Grinenko, V. et al. State with spontaneously broken time-reversal symmetry above the superconducting phase transition. Nat. Phys. 17, 1254–1259 (2021).
Shipulin, I. et al. Calorimetric evidence for two phase transitions in Ba1−xKxFe2As2 with fermion pairing and quadrupling states. Nat. Commun. 1, 6734 (2023).
Ferraretto, M., Richaud, A., Del Re, L., Fallani, L. & Capone, M. Enhancement of chiral edge currents in (d + 1)-dimensional atomic Mott-band hybrid insulators. SciPost Phys. 14, 048 (2023).
Medley, P., Weld, D. M., Miyake, H., Pritchard, D. E. & Ketterle, W. Spin gradient demagnetization cooling of ultracold atoms. Phys. Rev. Lett. 106, 195301 (2011).
Bakr, W. S., Gillen, J. I., Peng, A., Fölling, S. & Greiner, M. A quantum gas microscope for detecting single atoms in a Hubbard-regime optical lattice. Nature 462, 74–77 (2009).
Boll, M. et al. Spin- and density-resolved microscopy of antiferromagnetic correlations in Fermi-Hubbard chains. Science 353, 1257–1260 (2016).
Stamper-Kurn, D. M. & Ueda, M. Spinor Bose gases: symmetries, magnetism, and quantum dynamics. Rev. Mod. Phys. 85, 1191–1244 (2013).
Dutta, O. et al. Non-standard Hubbard models in optical lattices: a review. Rep. Prog. Phys. 78, 066001 (2015).
Luo, A. et al. Microscopic study on superexchange dynamics of composite spin-1 Bosons. Phys. Rev. Lett. 133, 043401 (2024).
Hauschild, J. & Pollmann, F. Efficient numerical simulations with tensor networks: tensor network Python (TeNPy). SciPost Phys. Lect. Notes https://doi.org/10.21468/SciPostPhysLectNotes.5 (2018).
Zheng, Y.-G. et al. Counterflow superfluidity in a two-component Mott insulator. figshare https://doi.org/10.6084/m9.figshare.27084313 (2024).
Acknowledgements
We acknowledge fruitful discussions with L.-X. Liu and N. Prokof’ev. This work was supported by the National Natural Science Foundation of China (Grant No. 12125409), the Innovation Programme for Quantum Science and Technology (Grant No. 2021ZD0302004) and the Anhui Initiative in Quantum Information Technologies. Y.D. acknowledged funds from the National Natural Science Foundation of China (Grant No. 12275263), the Innovation Programme for Quantum Science and Technology (Grant No. 2021ZD0301900) and Natural Science Foundation of Fujian Province of China (Grant No. 2023J02032). Y.-G.Z. acknowledged the support of the Fundamental Research Funds for the Central Universities, the CPS-Huawei MindSpore Fellowship and the China Postdoctoral Science Foundation (Grant No. 2023TQ0102).
Author information
Authors and Affiliations
Contributions
Y.-G.Z., Z.-S.Y. and J.-W.P. conceived the research and designed the experiments. Y.-G.Z., A.L., Y.-C.S., M.-G.H., Z.-H.Z., Y.L., W.-Y.Z. and H.S. performed the experiments and collected the data. Y.-G.Z. and A.L. analysed the data. Y.D., Z.-S.Y. and J.-W.P. supervised the research. All authors participated in writing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Four-particle dynamics in double wells.
We prepared the atoms into \(\left\vert {S}_{z}=0\right\rangle\) state in an array of double wells by imposing the y long lattice. Then the y short lattice is quenched to 10Er to start the dynamics in double wells. The dashed line is a sinusoidal curve fitting from which we inferred the anisotropy u.
Extended Data Fig. 2 TOF measurement of the noise correlations.
a and b show the noise correlations in the spin-Mott and CSF phases, respectively. Purple circles indicate the noise correlation of the both atoms while blue circles are that of the \(\left\vert \downarrow \right\rangle\) atoms. The inter-component noise correlations (orange circles) are obtained from the relation g↑↓(δy) = [g(δy) − 2g↓↓(δy)]/2 + 1/4.
Extended Data Fig. 3 Full-count statistics of the local magnetization in the spin-Mott (left panel) and xy-ferromagnet phases.
The distributions of the magnetization are broadened due to the superexchange process in the xy-ferromagnet phase.
Supplementary information
Supplementary Information
Supplementary Figs. 1–5, Discussion and Refs. 1–7.
Source data
Source Data Fig. 2
Statistical source data.
Source Data Fig. 3
Statistical source data.
Source Data Fig. 4
Statistical source data.
Source Data Extended Data Fig. 1
Statistical source data.
Source Data Extended Data Fig. 2
Statistical source data.
Source Data Extended Data Fig. 3
Statistical source data.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zheng, YG., Luo, A., Shen, YC. et al. Counterflow superfluidity in a two-component Mott insulator. Nat. Phys. 21, 208–213 (2025). https://doi.org/10.1038/s41567-024-02732-5
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41567-024-02732-5