Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Observation of Joule–Thomson photon-gas expansion

Nature Physics volume 21, pages 214–220 (2025)Cite this article

Subjects

Abstract

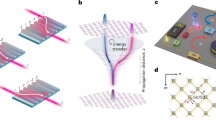
In recent years, a self-consistent optical thermodynamic framework has emerged that offers a systematic methodology to understand, harness and exploit the complex collective dynamics of multimode nonlinear systems. These developments now allow consideration of a series of long-standing problems in optics, including the prospect of funnelling the entire power flowing in a multimode system into its ground state, for which no methodology currently exists. Here we demonstrate an all-optical Joule–Thomson expansion process mediated by photon–photon interactions whereby the temperature of the optical gas drops abruptly to zero. Our experiments in various configurations of coupled multicore nonlinear waveguide arrangements illustrate how light undergoing expansion-induced cooling can be channelled from arbitrary input states into the fundamental mode with near-unity efficiency. We show that the stability of the post-expansion state is ensured through an irreversible process of energy conversion. The all-optical thermodynamic phenomena explored in this study may enable innovative techniques where various uncorrelated but identical sources are merged into a unified spatially coherent state, offering a route for direct beam combining.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Optical JT expansion effects.
Fig. 2: Experimental set-up.
Fig. 3: JT expansion in a triangular lattice.
Fig. 4: Impact of lattice connectivity, system shape and excitation position.

Similar content being viewed by others

Data availability

Source data are provided with this paper. Additional experimental data that support the findings of this study are available from M.S.K. upon reasonable request.

Code availability

The MATLAB codes that support the numerical analysis of this study are available from G.G.P.

References

  1. Chen, Z. & Segev, M. Highlighting photonics: looking into the next decade. eLight 1, 2 (2021).

    MATH  Google Scholar 

  2. Ahsan, A. S. & Agrawal, G. P. Graded-index solitons in multimode fibers. Opt. Lett. 43, 3345–3348 (2018).

    ADS  MATH  Google Scholar 

  3. Eisenberg, H. S., Silberberg, Y., Morandotti, R., Boyd, A. R. & Aitchison, J. S. Discrete spatial optical solitons in waveguide arrays. Phys. Rev. Lett. 81, 3383–3386 (1998).

    ADS  MATH  Google Scholar 

  4. Malomed, B. A., Mihalache, D., Wise, F. & Torner, L. Spatiotemporal optical solitons. J. Opt. B Quantum Semiclass. Opt. 7, R53–R72 (2005).

    ADS  MATH  Google Scholar 

  5. Morandotti, R., Peschel, U., Aitchison, J. S., Eisenberg, H. S. & Silberberg, Y. Dynamics of discrete solitons in optical waveguide arrays. Phys. Rev. Lett. 83, 2726–2729 (1999).

    ADS  MATH  Google Scholar 

  6. Renninger, W. H. & Wise, F. W. Optical solitons in graded-index multimode fibres. Nat. Commun. 4, 1719 (2013).

    ADS  MATH  Google Scholar 

  7. Segev, M., Crosignani, B., Yariv, A. & Fischer, B. Spatial solitons in photorefractive media. Phys. Rev. Lett. 68, 923–926 (1992).

    ADS  MATH  Google Scholar 

  8. Ablowitz, M. J., Prinari, B. & Trubatch, A. D. Discrete and Continuous Nonlinear Schrödinger Systems (Cambridge Univ. Press, 2003); https://doi.org/10.1017/CBO9780511546709

  9. Campbell, D. K., Flach, S. & Kivshar, Y. S. Localizing energy through nonlinearity and discreteness. Phys. Today 57, 43–49 (2004).

    ADS  MATH  Google Scholar 

  10. Longhi, S. Modulational instability and space time dynamics in nonlinear parabolic-index optical fibers. Opt. Lett. 28, 2363–2365 (2003).

    ADS  MATH  Google Scholar 

  11. Heinrich, M. et al. Observation of three-dimensional discrete-continuous X waves in photonic lattices. Phys. Rev. Lett. 103, 113903 (2009).

    ADS  MATH  Google Scholar 

  12. Tzortzakis, S., Prade, B., Franco, M. & Mysyrowicz, A. Time-evolution of the plasma channel at the trail of a self-guided IR femtosecond laser pulse in air. Opt. Commun. 181, 123–127 (2000).

    ADS  Google Scholar 

  13. Trompeter, H. et al. Bloch oscillations and Zener tunneling in two-dimensional photonic lattices. Phys. Rev. Lett. 96, 053903 (2006).

    ADS  Google Scholar 

  14. Morandotti, R., Peschel, U., Aitchison, J. S., Eisenberg, H. S. & Silberberg, Y. Experimental observation of linear and nonlinear optical Bloch oscillations. Phys. Rev. Lett. 83, 4756–4759 (1999).

    ADS  MATH  Google Scholar 

  15. Pourbeyram, H., Agrawal, G. P. & Mafi, A. Stimulated Raman scattering cascade spanning the wavelength range of 523 to 1750 nm using a graded-index multimode optical fiber. Appl. Phys. Lett. 102, 201107 (2013).

    ADS  Google Scholar 

  16. Boyd, R. W. & Gaeta, A. L. in Laser Optics of Condensed Matter (eds Garmire, E. et al.) 99–105 (Springer, 1991); https://doi.org/10.1007/978-1-4615-3726-7_15

  17. Podivilov, E. V. et al. Hydrodynamic 2D turbulence and spatial beam condensation in multimode optical fibers. Phys. Rev. Lett. 122, 103902 (2019).

    ADS  MATH  Google Scholar 

  18. Zakharov, V. E., L’vov, V. S. & Falkovich, G. Kolmogorov Spectra of Turbulence I (Springer, 1992); https://doi.org/10.1007/978-3-642-50052-7

  19. Klaers, J., Schmitt, J., Vewinger, F. & Weitz, M. Bose–Einstein condensation of photons in an optical microcavity. Nature 468, 545–548 (2010).

    ADS  Google Scholar 

  20. Wu, F. O., Hassan, A. U. & Christodoulides, D. N. Thermodynamic theory of highly multimoded nonlinear optical systems. Nat. Photon. 13, 776–782 (2019).

    ADS  MATH  Google Scholar 

  21. Picozzi, A. Towards a nonequilibrium thermodynamic description of incoherent nonlinear optics. Opt. Express 15, 9063–9083 (2007).

    ADS  MATH  Google Scholar 

  22. Aschieri, P., Garnier, J., Michel, C., Doya, V. & Picozzi, A. Condensation and thermalization of classsical optical waves in a waveguide. Phys. Rev. A 83, 033838 (2011).

    ADS  MATH  Google Scholar 

  23. Makris, K. G., Wu, Fan, O., Jung, P. S. & Christodoulides, D. N. Statistical mechanics of weakly nonlinear optical multimode gases. Opt. Lett. 45, 1651–1654 (2020).

  24. Ramos, A., Fernández-Alcázar, L., Kottos, T. & Shapiro, B. Optical phase transitions in photonic networks: a spin-system formulation. Phys. Rev. X 10, 031024 (2020).

    MATH  Google Scholar 

  25. Baudin, K. et al. Classical Rayleigh-Jeans condensation of light waves: observation and thermodynamic characterization. Phys. Rev. Lett. 125, 244101 (2020).

    ADS  MATH  Google Scholar 

  26. Shi, C., Kottos, T. & Shapiro, B. Controlling optical beam thermalization via band-gap engineering. Phys. Rev. Res. 3, 033219 (2021).

    MATH  Google Scholar 

  27. Wu, F. O. et al. Thermalization of light’s orbital angular momentum in nonlinear multimode waveguide systems. Phys. Rev. Lett. 128, 123901 (2022).

    ADS  MATH  Google Scholar 

  28. Jung, P. S. et al. Thermal control of the topological edge flow in nonlinear photonic lattices. Nat. Commun. 13, 4393 (2022).

    ADS  MATH  Google Scholar 

  29. Ferraro, M., Mangini, F., Zitelli, M. & Wabnitz, S. On spatial beam self-cleaning from the perspective of optical wave thermalization in multimode graded-index fibers. Adv. Phys. X 8, 2228018 (2023).

    Google Scholar 

  30. Mangini, F., Ferraro, M., Tonello, A., Couderc, V. & Wabnitz, S. High-temperature wave thermalization spoils beam self-cleaning in nonlinear multimode GRIN fibers. Opt. Lett. 48, 4741–4744 (2023).

    ADS  Google Scholar 

  31. Mangini, F. et al. Statistical mechanics of beam self-cleaning in GRIN multimode optical fibers. Opt. Express 30, 10850–10865 (2022).

    ADS  MATH  Google Scholar 

  32. Pourbeyram, H. et al. Direct observations of thermalization to a Rayleigh–Jeans distribution in multimode optical fibres. Nat. Phys. 18, 685–690 (2022).

    MATH  Google Scholar 

  33. Fusaro, A., Garnier, J., Krupa, K., Millot, G. & Picozzi, A. Dramatic acceleration of wave condensation mediated by disorder in multimode fibers. Phys. Rev. Lett. 122, 123902 (2019).

    ADS  MATH  Google Scholar 

  34. Barviau, B. et al. Experimental signature of optical wave thermalization through supercontinuum generation in photonic crystal fiber. Opt. Express 17, 7392–7406 (2009).

    ADS  MATH  Google Scholar 

  35. Podivilov, E. V. et al. Thermalization of orbital angular momentum beams in multimode optical fibers. Phys. Rev. Lett. 128, 243901 (2022).

    ADS  Google Scholar 

  36. Marques Muniz, A. L. et al. Observation of photon-photon thermodynamic processes under negative optical temperature conditions. Science 379, 1019–1023 (2023).

    ADS  MATH  Google Scholar 

  37. Baudin, K. et al. Observation of light thermalization to negative-temperature Rayleigh-Jeans equilibrium states in multimode optical fibers. Phys. Rev. Lett. 130, 063801 (2023).

    ADS  MATH  Google Scholar 

  38. Pyrialakos, G. G., Ren, H., Jung, P. S., Khajavikhan, M. & Christodoulides, D. N. Thermalization dynamics of nonlinear non-Hermitian optical lattices. Phys. Rev. Lett. 128, 213901 (2022).

    ADS  Google Scholar 

  39. Ren, H. et al. Nature of optical thermodynamic pressure exerted in highly multimoded nonlinear systems. Phys. Rev. Lett. 131, 193802 (2023).

    ADS  Google Scholar 

  40. Ren, H. et al. Dalton’s law of partial optical thermodynamic pressures in highly multimoded nonlinear photonic systems. Opt. Lett. 49, 1802–1805 (2024).

    ADS  MATH  Google Scholar 

  41. Pathria, R. K. & Beale, P. D. Statistical Mechanics (Academic, 2022).

  42. Selim, M. A., Wu, F. O., Pyrialakos, G. G., Khajavikhan, M. & Christodoulides, D. Coherence propertiesof light in highly multimoded nonlinear parabolic fibers under optical equilibrium conditions. Opt. Lett. 48, 1208–211 (2023).

    ADS  Google Scholar 

  43. Szameit, A. & Nolte, S. Discrete optics in femtosecond-laser-written photonic structures. J. Phys. B: Mol. Opt. Phys. 43, 163001 (2010).

    ADS  MATH  Google Scholar 

  44. Gerchberg, R. W. A new approach to phase retrieval of a wave front. J. Mod. Opt. 49, 1185–1196 (2002).

    ADS  MathSciNet  MATH  Google Scholar 

  45. Shapira, O., Abouraddy, A. F., Joannopoulos, J. D. & Fink, Y. Complete modal decomposition for optical waveguides. Phys. Rev. Lett. 94, 143902 (2005).

    ADS  Google Scholar 

  46. Schwartz, T., Bartal, G., Fishman, S. & Segev, M. Transport and Anderson localization in disordered two-dimensional photonic lattices. Nature 446, 52–55 (2007).

    ADS  MATH  Google Scholar 

  47. Trotzky, S. et al. Probing the relaxation towards equilibrium in an isolated strongly correlated one-dimensional Bose gas. Nat. Phys. 8, 325–330 (2012).

    Google Scholar 

  48. Anglin, J. R. & Ketterle, W. Bose–Einstein condensation of atomic gases. Nature 416, 211–218 (2002).

    ADS  MATH  Google Scholar 

  49. Mirhosseini, M., Sipahigil, A., Kalaee, M. & Painter, O. Superconducting qubit to optical photon transduction. Nature 588, 599–603 (2020).

    ADS  Google Scholar 

  50. Rückriegel, A. & Kopietz, P. Rayleigh-Jeans condensation of pumped magnons in thin-film ferromagnets. Phys. Rev. Lett. 115, 157203 (2015).

    ADS  MATH  Google Scholar 

Download references

Acknowledgements

We thank C. Otto for preparing the high-quality fused silica samples used for the inscription of all photonic structures employed in this work. A.S. acknowledges funding from the Deutsche Forschungsgemeinschaft (grants SZ 276/9-2, SZ 276/19-1, SZ 276/20-1, SZ 276/21-1, SZ 276/27-1 and GRK 2676/1-2023 ‘Imaging of Quantum Systems’, project no. 437567992). A.S. also acknowledges funding from the Krupp von Bohlen and Halbach Foundation as well as from the FET Open Grant EPIQUS (grant no. 899368) within the framework of the European H2020 programme for Excellent Science. A.S. and M.H. acknowledge funding from the Deutsche Forschungsgemeinschaft by means of SFB 1477 ‘Light–Matter Interactions at Interfaces’ (project no. 441234705). T.A.W.W. is supported by a European Commission Marie Skłodowska-Curie Actions Individual Fellowship ‘Quantum correlations in PT-symmetric photonic integrated circuits’, project no. 895254. This work was partially supported by the following agencies and organizations: W.M. Keck Foundation, Israel Ministry of Defense (4441279927), MPS Simons Collaboration (733682), National Science Foundation (CCF-2320937), Army Research Office (W911NF-23-1-0312), Office of Naval Research (N00014-20-1-2789), Air Force Office of Scientific Research (FA9550-20-1-0322, FA9550-21-1-0202), US Air Force Research Laboratory (FA86511820019, FA8650-19-C-1692) and the Department of Energy (DE-SC0022282, DE-SC0025224).

Author information

Author notes

  1. These authors contributed equally: Marco S. Kirsch, Georgios G. Pyrialakos.

Authors and Affiliations

  1. Institute of Physics, University of Rostock, Rostock, Germany

    Marco S. Kirsch, Richard Altenkirch, Julius Beck, Tom A. W. Wolterink, Alexander Szameit & Matthias Heinrich

  2. Ming Hsieh Department of Electrical and Computer Engineering, University of Southern California, Los Angeles, CA, USA

    Georgios G. Pyrialakos, Mahmoud A. Selim, Huizhong Ren, Mercedeh Khajavikhan & Demetrios N. Christodoulides

  3. College of Optics & Photonics-CREOL, University of Central Florida, Orlando, FL, USA

    Pawel S. Jung

Authors
  1. Marco S. Kirsch
    View author publications

    Search author on:PubMed Google Scholar

  2. Georgios G. Pyrialakos
    View author publications

    Search author on:PubMed Google Scholar

  3. Richard Altenkirch
    View author publications

    Search author on:PubMed Google Scholar

  4. Mahmoud A. Selim
    View author publications

    Search author on:PubMed Google Scholar

  5. Julius Beck
    View author publications

    Search author on:PubMed Google Scholar

  6. Tom A. W. Wolterink
    View author publications

    Search author on:PubMed Google Scholar

  7. Huizhong Ren
    View author publications

    Search author on:PubMed Google Scholar

  8. Pawel S. Jung
    View author publications

    Search author on:PubMed Google Scholar

  9. Mercedeh Khajavikhan
    View author publications

    Search author on:PubMed Google Scholar

  10. Alexander Szameit
    View author publications

    Search author on:PubMed Google Scholar

  11. Matthias Heinrich
    View author publications

    Search author on:PubMed Google Scholar

  12. Demetrios N. Christodoulides
    View author publications

    Search author on:PubMed Google Scholar

Contributions

G.G.P and D.N.C initiated the idea. G.G.P conceived the theoretical framework. M.S.K. and J.B. designed and fabricated the samples. The experimental set-up was constructed by M.S.K., T.A.W.W. and M.H. The measurements were conducted by M.S.K. Numerical simulations were performed by G.G.P, M.A.S., H.R. and P.S.J. The obtained data were evaluated and interpreted by M.S.K., R.A., M.H. and G.G.P. M.K., A.S. and D.N.C. supervised the efforts of their respective groups.

Corresponding authors

Correspondence to Georgios G. Pyrialakos or Demetrios N. Christodoulides.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Vincent Couderc and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Expansion in the presence of losses: BPM simulations.

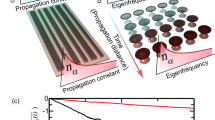
(a) In an ideal lossless system, the overall power is conserved, and the total power contained in the fundamental mode steadily grows during the cooling process. (b) The presence of losses introduces a global power decay (dashed red line), but the relative fraction of power contained in the fundamental mode (solid blue line) at a given propagation distance nevertheless increases as nonlinear expansion proceeds. As shown in Fig. 3b, even in the presence of significant propagation losses attenuation 0.3 dB/cm, a value beyond the typical losses of 0.4 dB/cm for laser-written waveguides in fused silica, the efficiency of the JT power transfer to the ground state only decreases by approximately 10%.

Source data

Extended Data Fig. 2 Nonlinear dynamics in the (b) square and (a,c) triangular lattices: tight-binding simulations.

In all lattices, light was injected from a single site with peak power favoring a JT irreversible expansion, just below the threshold of self-focusing collapse. The average (Rayleigh-Jeans) conversion efficiency to the fundamental mode is 85.3%, 79.3% and 91% for the, triangular (hexagonal), square, and triangular (irregular) lattice, respectively. An irreversible exchange of energy is observed between \(U\) and \({H}_{{NL}}\), matching almost perfectly with theoretical prediction. The teal dashed line represents Eq. 4 while the teal solid line includes a correction term, \({U}_{L}=-1/2{P}^{2}+{H}_{{NL},\min }=-1/2{P}^{2}+1/(2M){P}^{2}\).

Source data

Supplementary information

Supplementary Information

Supplementary Figs. 1–10 and Sections 1–8.

Source data

Source Data

Source data Figs. 1, 3 and 4 and Extended Data Figs. 1 and 2.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kirsch, M.S., Pyrialakos, G.G., Altenkirch, R. et al. Observation of Joule–Thomson photon-gas expansion. Nat. Phys. 21, 214–220 (2025). https://doi.org/10.1038/s41567-024-02736-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-024-02736-1

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing