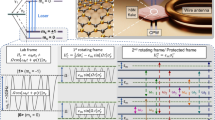
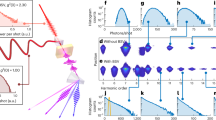
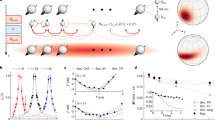
Abstract
Ultrasensitive detection of the frequency, phase and amplitude of radiofrequency electric fields is crucial for applications in radio communication, cosmology, dark matter searches and high-fidelity qubit control. Quantum harmonic oscillator systems, especially trapped ions, offer high-sensitivity electric field sensing with nanometre spatial resolution but are typically restricted to narrow frequency ranges centred around the motional frequency of the trapped-ion oscillator or the frequency of an optical transition in the ion. Here we present a procedure that enables precise electric field detection over an expanded frequency range. Specifically, we use motional Raman transitions in a single trapped ion to achieve sensitivity across a frequency range over 800 times larger than previous approaches. We show that the method is compatible with both quantum amplification via squeezing and measurement in the Fock basis, allowing a demonstration of performance 3.4(2.0) dB below the standard quantum limit. The approach can be extended to other quantum harmonic oscillator systems, such as superconducting qubit–resonator systems.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Source data are provided with this paper. All other data relevant to this study are available from the corresponding author upon reasonable request.
References
Giovannetti, V. et al. Quantum-enhanced measurements: beating the standard quantum limit. Science 306, 1330–1336 (2004).
Pezzè, L. et al. Quantum metrology with nonclassical states of atomic ensembles. Rev. Mod. Phys. 90, 035005 (2018).
Degen, C. et al. Quantum sensing. Rev. Mod. Phys. 89, 035002 (2017).
Wolf, F. et al. Motional Fock states for quantum-enhanced amplitude and phase measurements with trapped ions. Nat. Commun. 10, 2929 (2019).
McCormick, K. et al. Quantum-enhanced sensing of a single-ion mechanical oscillator. Nature 572, 86–90 (2019).
Deng, X. et al. Quantum-enhanced metrology with large Fock states. Nat. Phys. 20, 1874–1880 (2024).
Burd, S. et al. Quantum amplification of mechanical oscillator motion. Science 364, 1163–1165 (2019).
Gilmore, K. et al. Quantum-enhanced sensing of displacements and electric fields with two-dimensional trapped-ion crystals. Science 373, 673–678 (2021).
Zhang, J. et al. NOON states of nine quantized vibrations in two radial modes of a trapped ion. Phys. Rev. Lett. 121, 160502 (2018).
Milne, A. et al. Quantum oscillator noise spectroscopy via displaced cat states. Phys. Rev. Lett. 126, 250506 (2021).
Keller, J. et al. Quantum harmonic oscillator spectrum analyzers. Phys. Rev. Lett. 126, 250507 (2021).
Gilmore, K. et al. Amplitude sensing below the zero-point fluctuations with a two-dimensional trapped-ion mechanical oscillator. Phys. Rev. Lett. 118, 263602 (2017).
Affolter, M. et al. Phase-coherent sensing of the center-of-mass motion of trapped-ion crystals. Phys. Rev. A 102, 052609 (2020).
Schirhagl, R. et al. Nitrogen-vacancy centers in diamond: nanoscale sensors for physics and biology. Annu. Rev. Phys. Chem. 65, 83–105 (2014).
Qiu, Z. et al. Nanoscale electric field imaging with an ambient scanning quantum sensor microscope. npj Quantum Inf. 8, 107 (2022).
Liu, B. et al. Highly sensitive measurement of a megahertz RF electric field with a Rydberg-atom sensor. Phys. Rev. Appl. 18, 014045 (2022).
Holloway, C. et al. Rydberg atom-based field sensing enhancement using a split-ring resonator. Appl. Phys. Lett. 120, 204001 (2022).
Hempel, C. et al. Entanglement-enhanced detection of single-photon scattering events. Nat. Photon. 7, 630–633 (2013).
Day, M. et al. Limits on atomic qubit control from laser noise. npj Quantum Inf. 8, 72 (2022).
Burd, S. et al. Experimental speedup of quantum dynamics through squeezing. PRX Quantum 5, 020314 (2024).
Hudson, E. et al. Laserless quantum gates for electric dipoles in thermal motion. Phys. Rev. A 104, 042605 (2021).
Ge, W. et al. Trapped ion quantum information processing with squeezed phonons. Phys. Rev. Lett. 122, 030501 (2019).
Burd, S. et al. Quantum amplification of boson-mediated interactions. Nat. Phys. 17, 898–902 (2021).
Roos, C. et al. Quantum state engineering on an optical transition and decoherence in a Paul trap. Phys. Rev. Lett. 83, 4713–4716 (1999).
Leibfried, D. et al. Quantum dynamics of single trapped ions. Rev. Mod. Phys. 75, 281–324 (2003).
Zarantonello, G. et al. Robust and resource-efficient microwave near-field entangling 9Be+ gate. Phys. Rev. Lett. 123, 260503 (2019).
Moses, S. et al. A race-track trapped-ion quantum processor. Phys. Rev. X 13, 041052 (2023).
Natarajan, V. et al. Classical squeezing of an oscillator for subthermal noise operation. Phys. Rev. Lett. 74, 2855 (1995).
Meyer, D. et al. Assessment of Rydberg atoms for wideband electric field sensing. J. Phys. B 53, 034001 (2020).
Johnson, K. et al. Ultrafast creation of large Schrödinger cat states of an atom. Nat. Commun. 8, 697 (2017).
Monroe, C. et al. A ‘Schrödinger cat’ superposition state of an atom. Science 272, 1131–1136 (1996).
Yamamoto, T. et al. Flux-driven Josephson parametric amplifier. Appl. Phys. Lett. 93, 042510 (2008).
Jerger, M. et al. In situ characterization of qubit control lines: a qubit as a vector network analyzer. Phys. Rev. Lett. 123, 150501 (2019).
Gely, M. et al. In situ characterization of qubit-drive phase distortions. Phys. Rev. Appl. 22, 024001 (2024).
Matthiesen, C. et al. Trapping electrons in a room-temperature microwave Paul trap. Phys. Rev. X 11, 011019 (2021).
Xu, J. et al. Data processing over single-port homodyne detection to realize superresolution and supersensitivity. Phys. Rev. A 100, 063839 (2019).
Acknowledgements
We thank S. C. Burd, P. Hamilton and W. C. Campbell for helpful discussions. This work was supported by the National Science Foundation (grant numbers PHY-2110421 and OMA-2016245), Air Force Office of Scientific Research (grant number 130427-5114546) and Army Research Office (grant number W911NF-19-1-0297).
Author information
Authors and Affiliations
Contributions
H.W. and E.R.H. conceived the experiments. H.W., G.D.M., and C.Z.C.H. built and maintained the experimental set-up. H.W., G.D.M., C.Z.C.H. and J.A.R. carried out the measurements. E.R.H. supervised all work. All authors discussed the results and contributed to the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Transfer function of a commercial low pass filter (Mini-Circuits: SLP-100+) measured by the QVSA and a commercial vector network analyzer (VNA).
(a-b) \(\circ\) and \(\diamond\) are measured through the QVSA. Solid lines are measured via a commercial vector network analyzer. Each point is composed of N ≈ 13500 experiments. The excellent agreement confirms the accuracy of the QVSA technique. Error bars represent one standard error. No re-scaling or offset is applied to the data. See the SI for details.
Extended Data Fig. 2 Insertion loss of the ion trap system measured using the QVSA and a commercial vector network analyzer (VNA).
The wideband transfer function of a qubit control line is compared against that from a traditional measurement using a capacitor divider connected to trapping RF electrodes and a vector network analyzer over the frequency range accessible with our DDS (20 MHz - 300 MHz). The traditional measurement fails to accurately report the filter function. Changes to the measurement conditions required to interface the network analyzer, for example impedance changes at measurement ports, likely account for this discrepancy, serving as an archetypal example of the difficulty of accurately calibrating qubit signals. Blue (red) data shows the insertion loss measured by the QVSA (VNA). Error bars for the QVSA measurements represent one standard error and are too small to be seen.
Supplementary information
Supplementary Information
Supplementary Figs. 1–10 and Appendices A–I.
Source data
Source Data Fig. 2
Source data.
Source Data Fig. 3
Source data.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wu, H., Mitts, G.D., Ho, C.Z.C. et al. Wideband electric field quantum sensing via motional Raman transitions. Nat. Phys. 21, 380–385 (2025). https://doi.org/10.1038/s41567-024-02753-0
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41567-024-02753-0
This article is cited by
-
Ultrasensitive single-ion electrometry in a magnetic field gradient
Nature Physics (2025)