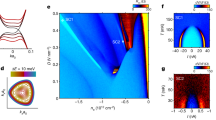
Abstract
Superconductivity is a common feature of graphite allotropes, having been observed in Bernal bilayers, rhombohedral trilayers and a wide variety of angle-misaligned multilayers. Despite notable differences in the electronic structure of these systems, supporting the graphite on a WSe2 substrate has been consistently observed to expand the range of the superconductivity in terms of carrier density and temperature. Here we report the observation of two distinct superconducting states in Bernal bilayer graphene with strong proximity-induced Ising spin–orbit coupling. Our quantum oscillation measurements show that, although the normal state of the first superconducting phase is consistent with the single-particle band structure, the second emerges from a nematic normal state with broken rotational symmetry. Both superconductors are robust to in-plane magnetic fields, but neither reach fields expected for spin–valley-locked Ising superconductors. The Fermi surface geometry of the first superconducting phase suggests that the superconductivity is limited by orbital depairing arising from the imperfect layer polarization of the electron wavefunctions. Finally, an analysis of transport and thermodynamic compressibility measurements in the second superconducting phase shows that the proximity to isospin phase boundaries, observed in other rhombohedral graphene allotropes, is probably coincidental, thus constraining theories of the pairing mechanisms in these systems.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All the experimental data used in this work are available via Zenodo at https://doi.org/10.5281/zenodo.14370753 (ref. 57). Source data are provided with this paper.
References
Sigrist, M., Avella, A. & Mancini, F. Introduction to unconventional superconductivity in non-centrosymmetric metals. AIP Conf. Proc. 55, 55–96 (2009).
Bauer, E. & Sigrist, M. (eds.) Non-Centrosymmetric Superconductors, Vol. 847 of Lecture Notes in Physics (Springer, 2012).
Lu, J. M. et al. Evidence for two-dimensional Ising superconductivity in gated MoS2. Science 350, 1353–1357 (2015).
Xi, X. et al. Ising pairing in superconducting NbSe2 atomic layers. Nat. Phys. 12, 139–143 (2016).
Saito, Y. et al. Superconductivity protected by spin-valley locking in ion-gated MoS2. Nat. Phys. 12, 144–149 (2016).
Möckli, D. & Khodas, M. Ising superconductors: interplay of magnetic field, triplet channels, and disorder. Phys. Rev. B 101, 014510 (2020).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059–1064 (2019).
Hao, Z. et al. Electric field-tunable superconductivity in alternating-twist magic-angle trilayer graphene. Science 371, 1133–1138 (2021).
Park, J. M., Cao, Y., Watanabe, K., Taniguchi, T. & Jarillo-Herrero, P. Tunable strongly coupled superconductivity in magic-angle twisted trilayer graphene. Nature 590, 249–255 (2021).
Cao, Y., Park, J. M., Watanabe, K., Taniguchi, T. & Jarillo-Herrero, P. Pauli-limit violation and re-entrant superconductivity in moiré graphene. Nature 595, 526–531 (2021).
Zhang, Y. et al. Promotion of superconductivity in magic-angle graphene multilayers. Science 377, 1538–1543 (2022).
Park, J. M. et al. Robust superconductivity in magic-angle multilayer graphene family. Nat. Mater. 21, 877–883 (2022).
Zhou, H., Xie, T., Taniguchi, T., Watanabe, K. & Young, A. F. Superconductivity in rhombohedral trilayer graphene. Nature 598, 434–438 (2021).
Zhou, H. et al. Isospin magnetism and spin-polarized superconductivity in Bernal bilayer graphene. Science 375, 774–778 (2022).
Sichau, J. et al. Resonance microwave measurements of an intrinsic spin–orbit coupling gap in graphene: a possible indication of a topological state. Phys. Rev. Lett. 122, 46403 (2019).
Arp, T. et al. Intervalley coherence and intrinsic spin–orbit coupling in rhombohedral trilayer graphene. Nat. Phys. 20, 1413–1420 (2024).
Avsar, A. et al. Spin–orbit proximity effect in graphene. Nat. Commun. 5, 4875 (2014).
Wang, Z. et al. Strong interface-induced spin–orbit interaction in graphene on WS2. Nat. Commun. 6, 8339 (2015).
Wang, Z. et al. Origin and magnitude of ‘designer’ spin–orbit interaction in graphene on semiconducting transition metal dichalcogenides. Phys. Rev. X 6, 041020 (2016).
Yang, B. et al. Strong electron-hole symmetric Rashba spin–orbit coupling in graphene/monolayer transition metal dichalcogenide heterostructures. Phys. Rev. B 96, 041409(R) (2017).
Völkl, T. et al. Magnetotransport in heterostructures of transition metal dichalcogenides and graphene. Phys. Rev. B 96, 125405 (2017).
Zihlmann, S. et al. Large spin relaxation anisotropy and valley-Zeeman spin–orbit coupling in WSe2/graphene/h-BN heterostructures. Phys. Rev. B 97, 075434 (2018).
Wakamura, T. et al. Strong anisotropic spin–orbit interaction induced in graphene by monolayer WS2. Phys. Rev. Lett. 120, 106802 (2018).
Wang, D. et al. Quantum Hall effect measurement of spin–orbit coupling strengths in ultraclean bilayer graphene/WSe2 heterostructures. Nano Lett. 19, 7028–7034 (2019).
Arora, H. S. et al. Superconductivity in metallic twisted bilayer graphene stabilized by WSe2. Nature 583, 379 (2020).
Lin, J. X. et al. Zero-field superconducting diode effect in small-twist-angle trilayer graphene. Nat. Phys. 18, 1221–1227 (2022).
Su, R., Kuiri, M., Watanabe, K., Taniguchi, T. & Folk, J. Superconductivity in twisted double bilayer graphene stabilized by WSe2. Nat. Mater. 22, 1332–1337 (2023).
Lau, C. N., Bockrath, M. W., Mak, K. F. & Zhang, F. Reproducibility in the fabrication and physics of moiré materials. Nature 602, 41–50 (2022).
Zhang, Y. et al. Enhanced superconductivity in spin–orbit proximitized bilayer graphene. Nature 613, 268–273 (2023).
de la Barrera, S. C. et al. Cascade of isospin phase transitions in Bernal-stacked bilayer graphene at zero magnetic field. Nat. Phys. 18, 771–775 (2022).
Island, J. O. et al. Spin–orbit-driven band inversion in bilayer graphene by the van der Waals proximity effect. Nature 571, 85–89 (2019).
Jung, J. & MacDonald, A. H. Accurate tight-binding models for the π bands of bilayer graphene. Phys. Rev. B 89, 035405 (2014).
McCann, E. & Fal’ko, V. I. Landau-level degeneracy and quantum Hall effect in a graphite bilayer. Phys. Rev. Lett. 96, 086805 (2006).
Khoo, J. Y. & Levitov, L. Tunable quantum Hall edge conduction in bilayer graphene through spin–orbit interaction. Phys. Rev. B 98, 115307 (2018).
Zhang, Y. et al. Direct observation of a widely tunable bandgap in bilayer graphene. Nature 459, 820–823 (2009).
Biberacher, W. in Encyclopedia of Condensed Matter Physics (eds Bassani, F. et al.) 360–368 (Elsevier, 2005).
Cao, Y. et al. Nematicity and competing orders in superconducting magic-angle graphene. Science 372, 264–271 (2021).
Lin, J.-X. et al. Spontaneous momentum polarization and diodicity in Bernal bilayer graphene. Preprint at https://doi.org/10.48550/arXiv.2302.04261 (2023).
Zhang, N. J. et al. Angle-resolved transport non-reciprocity and spontaneous symmetry breaking in twisted trilayer graphene. Nat. Mater. 23, 356–362 (2024).
Lemonik, Y., Aleiner, I. L., Toke, C. & Fal’Ko, V. I. Spontaneous symmetry breaking and Lifshitz transition in bilayer graphene. Phys. Rev. B 82, 201408(R) (2010).
Vafek, O. & Yang, K. Many-body instability of Coulomb interacting bilayer graphene: renormalization group approach. Phys. Rev. B 81, 041401(R) (2010).
Mayorov, A. S. et al. Interaction-driven spectrum reconstruction in bilayer graphene. Science 333, 860–863 (2011).
Dong, Z., Davydova, M., Ogunnaike, O. & Levitov, L. Isospin- and momentum-polarized orders in bilayer graphene. Phys. Rev. B 107, 075108 (2023).
Huang, C. et al. Spin and orbital metallic magnetism in rhombohedral trilayer graphene. Phys. Rev. B 107, L121405 (2023).
Szabó, A. L. & Roy, B. Competing orders and cascade of degeneracy lifting in doped Bernal bilayer graphene. Phys. Rev. B 105, L201107 (2022).
Curtis, J. B. et al. Stabilizing fluctuating spin-triplet superconductivity in graphene via induced spin–orbit coupling. Phys. Rev. Lett. 130, 196001 (2023).
Chatterjee, S., Wang, T., Berg, E. & Zaletel, M. P. Inter-valley coherent order and isospin fluctuation mediated superconductivity in rhombohedral trilayer graphene. Nat. Commun. 13, 6013 (2022).
Xie, M. & Sarma, S. D. Flavor symmetry breaking in spin–orbit coupled bilayer graphene. Phys. Rev. B 107, L201119 (2023).
Wagner, G., Kwan, Y. H., Bultinck, N., Simon, S. H. & Parameswaran, S. A. Superconductivity from repulsive interactions in Bernal-stacked bilayer graphene. Preprint at https://doi.org/10.48550/arXiv.2302.00682 (2023).
Chou, Y. Z., Wu, F. & Das Sarma, S. Enhanced superconductivity through virtual tunneling in Bernal bilayer graphene coupled to WSe2. Phys. Rev. B 106, L180502 (2022).
Jimeno-Pozo, A., Sainz-Cruz, H., Cea, T., Pantaleón, P. A. & Guinea, F. Superconductivity from electronic interactions and spin–orbit enhancement in bilayer and trilayer graphene. Phys. Rev. B 107, L161106 (2023).
Shavit, G. & Oreg, Y. Inducing superconductivity in bilayer graphene by alleviation of the Stoner blockade. Phys. Rev. B 108, 024510 (2023).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Zibrov, A. A. et al. Tunable interacting composite fermion phases in a half-filled bilayer-graphene Landau level. Nature 549, 360–364 (2017).
Zhou, H. et al. Half- and quarter-metals in rhombohedral trilayer graphene. Nature 598, 429–433 (2021).
Holleis, L. et al. Nematicity and orbital depairing in superconducting Bernal bilayer graphene. Zenodo https://doi.org/10.5281/zenodo.14370753 (2024).
Acknowledgements
We acknowledge discussions with M. Serbyn, A. Ghazaryan, A. H. MacDonald, Z. Dong, M. Khodas and P. A. Lee. The work was supported by the Office of Naval Research (award N00014-20-1-2609) and the Gordon and Betty Moore Foundation (award GBMF9471). The work at Caltech was supported by an NSF-CAREER award (DMR-1753306). K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by MEXT, Japan (grant no. JPMXP0112101001) and JSPSKAKENHI (grant nos. 19H05790, 20H00354 and 21H05233). E.B. and Y.V. were supported by NSF-BSF award DMR-2310312 and by the European Research Council under grant HQMAT (grant agreement no. 817799).
Author information
Authors and Affiliations
Contributions
L.H. and A.F.Y. conceived the project. L.H., Y.Z. and H.Z. designed and fabricated the devices. K.W. and T.T. grew the hBN crystals. L.H., C.L.P., H.M.Y. and A.F.Y. performed the transport and capacitance measurements and analysed the data. Y.V. and E.B. contributed to the theoretical interpretation and performed the numerical calculations. L.H., E.B., S.N.-P. and A.F.Y. wrote the paper with input from all the other authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Yuan Cao and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Measurement of Ising SOC from transitions in the lowest Landau level (LL).
(A - E) D − ne phase diagrams for different out-of-plane magnetic fields B⊥ at low displacement fields. The black arrows mark the orbital transitions of the ν = ± 3 LL used to determine the Ising SOC. (F) B⊥ dependent transitions plotted against D. The dashed lines are fits to the data. The Ising SOC is calculated from the crossing point of the ν = ± 3 lines32. Data from this device taken at higher temperatures and without in-plane magnetic fields was previously described in Ref. 30.
Extended Data Fig. 2 Additional bias and temperature dependence of SC1 and SC2.
(A) linecut of the dV/dI spectrum of Fig. 1f at zero field and ne = − 8.7 ⋅ 1011cm−2 and D = 0.95 V/nm. (B) Temperature dependence of panel A. (C) I-V characteristics extracted from temperature dependent non-linear transport data of SC2 in (D) at ne = − 7.3 ⋅ 1011cm−2 and D = 1.15 V/nm. The dashed line in C is a fit where V ~ I3 which we define as the BKT-transition temperature.
Extended Data Fig. 3 Raw quantum oscillation data.
(A - B) Shubnikov-de-Haas data taken at D = 0.95 V/nm and 1.15 V/nm, respectively. (C) B⊥ dependent inverse compressibility determined from penetration field capacitance data at D = 0.95 V/nm. The white arrows in A and C indicate the Landau fan associated with the small electron annulus in the Ising2,2,−2 phase. (D) Same data as in panel B plotted as density ne over B⊥. An average background is subtracted from the raw data to visually enhance the quantum oscillations and illustrate no obvious change of quantum oscillations across the COS around ne = − 6.9 ⋅ 1011cm−2.
Extended Data Fig. 4 Shubnikov-de-Haas measurements and fermiology analysis at D = 1.05 V/nm.
(A) raw quantum oscillation data which is used to compute the Fourier transform in panel C. The white arrows indicate electron like quantum oscillations associated with f3. (B) comparison of Rxx and inverse compressibility κ at zero magnetic field. (C) Fourier transform of the data in A for fields from 150 - 300 mT similar to main text Fig. 2b. The region of SC1,2 are indicated by the white dashed lines. As SC1 is not well formed and is barely visible in Rxx, one should confirm its location with the 2D resistance map in Fig. S10. Note: due to the higher field range used here compared to the main text, additional peaks associated with magnetic breakdown effects between different pockets of f4,5 are apparent. (D) Schematic of panel C with main frequencies extracted via Gaussian fits to the data (f3 is not well captured by fits and extracted manually here). Shaded areas represent error bars corresponding to the standard deviation of Gaussian fits to the peak frequencies The same phases as in the main text Fig. 2 are observed, most importantly showing the transition to the nematic N2,4 phase.
Extended Data Fig. 5 Magnetic breakdown between the small Fermi pockets.
(A - C) Fourier transformation of the data in Extended Data Fig. 3A taken over different field ranges. The white arrows mark f4 and f4,breakdown. (D) Field range dependent FFT amplitude averaged over densities between − 8.49 ⋅ 1011cm−2 to − 8.3 ⋅ 1011 cm−2. The relative weight between f4 and f4,breakdown increases in favor of the latter for a larger and higher B⊥,range, illustrating that f4,breakdown is due to magnetic breakdown between the fermi pockets associated with the frequency f4.
Extended Data Fig. 6 Bandstructure fits to quantum oscillations.
Experimental Shubnikov–de Haas oscillation frequencies (dots) with theoretical fits to the data (lines) for three different displacement fields 0.8 V/nm (A), 0.95 V/nm (B) and 1.05 V/nm (C). We find γ0 = 2880 meV, γ1 = 361 meV, γ3 = 323 meV, γ4 = 30 meV, δ = 13 meV with Ising SOC set to λII = 1.6 meV from fits to single particle calculations. These values are used to calculate the in-plane orbital pair breaking.
Extended Data Fig. 7 In-plane critical fields including orbital and Rashba SOC effects.
Analogous calculations to those of Fig. 3c of the main text, including both orbital depairing and the effect of Rashba spin orbit coupling with values ranging from 0.5 - 2 meV.
Extended Data Fig. 8 In-plane field dependence of SC1 at D = 0.94 V/nm.
(A - C) Tc domes for different in-plane magnetic fields B∥ up to 0.1 T.
Extended Data Fig. 9 Critical temperature extraction from superconducting domes.
R-T linecuts from which in-plane field dependent critical temperatures are extracted. Both raw data and fits to the data are plotted. A-C display the three different ne, D values. Experimental values in Fig. 3b are taken from panel B.
Extended Data Fig. 10 Comparison of transport and penetration field capacitance.
(A - B) ne − D phase diagram of Rxx and κ over a larger density range than Fig. 4d, including SC1. The superconducting regions are overlaid from transport onto the inverse compressibility map via the white dashed line. (C) linecuts of Rxx and κ at D = 0.95 V/nm across SC1. The noise of κ gives an upper bound of ~ 300 mK on a possible chemical potential jump due to a first order phase transition below our experimental resolution. The fermiology is added as determined in Fig. 2. (D) same as Fig. 4c for a different D = 1.1 V/nm. (E - F) κ (top panel) and Rxx (bottom panel) linecuts at D = 0.95 V/nm and 1.1 V/nm. At low ∣ne∣, several negative spikes in κ become apparent - illustrating the sensitivity of κ to first order phase transitions. The dashed lines mark zero as guide to the eye.
Supplementary information
Supplementary Information
Band structure calculations, critical temperature calculations with an in-plane magnetic field, supplementary discussion on the competing order state and Supplementary Figs. 1–5.
Source data
Source Data Fig. 1
Zip file containing .txt files of the experimental data.
Source Data Fig. 2
Zip file containing .txt files of the experimental data.
Source Data Fig. 3
Zip file containing .txt files of the experimental data.
Source Data Fig. 4
Zip file containing .txt files of the experimental data.
Source Data Extended Data Fig. 1
Zip file containing .txt files of the experimental data.
Source Data Extended Data Fig. 2
Zip file containing .txt files of the experimental data.
Source Data Extended Data Fig. 3
Zip file containing .txt files of the experimental data.
Source Data Extended Data Fig. 4
Zip file containing .txt files of the experimental data.
Source Data Extended Data Fig. 5
Zip file containing .txt files of the experimental data.
Source Data Extended Data Fig. 6
Zip file containing .txt files of the experimental data.
Source Data Extended Data Fig. 7
Zip file containing .txt files of the experimental data.
Source Data Extended Data Fig. 8
Zip file containing .txt files of the experimental data.
Source Data Extended Data Fig. 9
Zip file containing .txt files of the experimental data.
Source Data Extended Data Fig. 10
Zip file containing .txt files of the experimental data.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Holleis, L., Patterson, C.L., Zhang, Y. et al. Nematicity and orbital depairing in superconducting Bernal bilayer graphene. Nat. Phys. 21, 444–450 (2025). https://doi.org/10.1038/s41567-024-02776-7
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41567-024-02776-7
This article is cited by
-
Isospin magnetic texture and intervalley exchange interaction in rhombohedral tetralayer graphene
Nature Physics (2025)
-
Twist-programmable superconductivity in spin–orbit-coupled bilayer graphene
Nature (2025)
-
Fluctuating magnetism and Pomeranchuk effect in multilayer graphene
Nature (2025)
-
Superconductivity and quantized anomalous Hall effect in rhombohedral graphene
Nature (2025)
-
Ephemeral superconductivity atop the false vacuum
Nature Communications (2025)