Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Detection of fractional quantum Hall states by entropy-sensitive measurements

Nature Physics volume 21, pages 724–731 (2025)Cite this article

Subjects

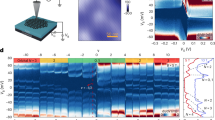
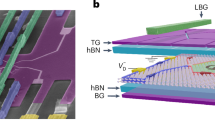
Abstract

The thermopower of a clean two-dimensional electron system is directly proportional to the entropy per charge carrier and can probe strongly interacting quantum phases such as fractional quantum Hall liquids. In particular, thermopower is a valuable parameter to probe the quasiparticle statistics that give rise to excess entropy in certain even-denominator fractional quantum Hall states. Here we demonstrate that the magneto-thermopower detection of fractional quantum Hall states is more sensitive than resistivity measurements. We do this in the context of Bernal-stacked bilayer graphene and highlight several even-denominator states at a relatively low magnetic field. These capabilities of thermopower measurements support the interest in fractional quantum Hall states for finding quasiparticles with non-Abelian statistics and elevate bilayer graphene as a promising platform for achieving this.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Thermopower measurements in the IQH regime.
Fig. 2: Thermopower measurements in the FQH regime.
Fig. 3: Energy gaps of even-denominator FQH states.
Fig. 4: Excess entropy of even-denominator FQH states.

Similar content being viewed by others

Data availability

The data that support the findings of this study are available from the George Mason University Dataverse at https://doi.org/10.13021/orc2020/681UPS (ref. 42). Source data are provided with this paper.

References

  1. Tsui, D. C., Stormer, H. L. & Gossard, A. C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 48, 1559–1562 (1982).

    Article  ADS  Google Scholar 

  2. Willett, R. et al. Observation of an even-denominator quantum number in the fractional quantum Hall effect. Phys. Rev. Lett. 59, 1776–1779 (1987).

    Article  ADS  Google Scholar 

  3. Kitaev, A. Y. Fault-tolerant quantum computation by anyons. Ann. Phys. 303, 2–30 (2003).

    Article  ADS  MathSciNet  Google Scholar 

  4. Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083 (2008).

    Article  ADS  MathSciNet  Google Scholar 

  5. Jain, J. K. Composite-fermion approach for the fractional quantum Hall effect. Phys. Rev. Lett. 63, 199–202 (1989).

    Article  ADS  Google Scholar 

  6. Jain, J. K. Composite Fermions (Cambridge Univ. Press, 2007).

  7. Feldman, D. E. & Halperin, B. I. Fractional charge and fractional statistics in the quantum Hall effects. Rep. Prog. Phys. 84, 076501 (2021).

    Article  MathSciNet  Google Scholar 

  8. Ma, K. K. W. & Feldman, D. E. The sixteenfold way and the quantum Hall effect at half-integer filling factors. Phys. Rev. B 100, 035302 (2019).

    Article  ADS  Google Scholar 

  9. Suen, Y. W., Engel, L. W., Santos, M. B., Shayegan, M. & Tsui, D. C. Observation of a v = 1/2 fractional quantum Hall state in a double-layer electron system. Phys. Rev. Lett. 68, 1379–1382 (1992).

    Article  ADS  Google Scholar 

  10. Bolotin, K. I., Ghahari, F., Shulman, M. D., Stormer, H. L. & Kim, P. Observation of the fractional quantum Hall effect in graphene. Nature 462, 196–199 (2009).

    Article  ADS  Google Scholar 

  11. Du, X., Skachko, I., Duerr, F., Luican, A. & Andrei, E. Y. Fractional quantum Hall effect and insulating phase of Dirac electrons in graphene. Nature 462, 192–195 (2009).

    Article  ADS  Google Scholar 

  12. Ghahari, F., Zhao, Y., Cadden-Zimansky, P., Bolotin, K. & Kim, P. Measurement of the ν = 1/3 fractional quantum Hall energy gap in suspended graphene. Phys. Rev. Lett. 106, 046801 (2011).

    Article  ADS  Google Scholar 

  13. Ki, D.-K., Fal’ko, V. I., Abanin, D. A. & Morpurgo, A. F. Observation of even denominator fractional quantum Hall effect in suspended bilayer graphene. Nano Lett. 14, 2135–2139 (2014).

    Article  ADS  Google Scholar 

  14. Kim, Y. et al. Fractional quantum Hall states in bilayer graphene probed by transconductance fluctuations. Nano Lett. 15, 7445–7451 (2015).

    Article  ADS  Google Scholar 

  15. Falson, J. et al. Even-denominator fractional quantum Hall physics in ZnO. Nat. Phys. 11, 347–351 (2015).

    Article  ADS  Google Scholar 

  16. Zibrov, A. A. et al. Tunable interacting composite fermion phases in a half-filled bilayer-graphene Landau level. Nature 549, 360–364 (2017).

    Article  ADS  Google Scholar 

  17. Li, J. I. A. et al. Even-denominator fractional quantum Hall states in bilayer graphene. Science 358, 648–652 (2017).

    Article  ADS  Google Scholar 

  18. Zibrov, A. A. et al. Even-denominator fractional quantum Hall states at an isospin transition in monolayer graphene. Nat. Phys. 14, 930–935 (2018).

    Article  Google Scholar 

  19. Falson, J. et al. A cascade of phase transitions in an orbitally mixed half-filled Landau level. Sci. Adv. 4, eaat8742 (2018).

    Article  ADS  Google Scholar 

  20. Kim, Y. et al. Even denominator fractional quantum Hall states in higher Landau levels of graphene. Nat. Phys. 15, 154–158 (2019).

    Article  Google Scholar 

  21. Shi, Q. et al. Odd- and even-denominator fractional quantum Hall states in monolayer WSe2. Nat. Nanotechnol. 15, 569–573 (2020).

    Article  ADS  Google Scholar 

  22. Papić, Z., Abanin, D. A., Barlas, Y. & Bhatt, R. N. Tunable interactions and phase transitions in Dirac materials in a magnetic field. Phys. Rev. B 84, 241306 (2011).

    Article  ADS  Google Scholar 

  23. Apalkov, V. M. & Chakraborty, T. Stable Pfaffian state in bilayer graphene. Phys. Rev. Lett. 107, 186803 (2011).

    Article  ADS  Google Scholar 

  24. Papić, Z. & Abanin, D. A. Topological phases in the zeroth Landau level of bilayer graphene. Phys. Rev. Lett. 112, 046602 (2014).

    Article  ADS  Google Scholar 

  25. Obraztsov, Yu. N. The thermal EMF of semiconductors in a quantizing magnetic field. Fiz. Tverd. Tela 7, 573–581 (1965).

    Google Scholar 

  26. Yang, K. & Halperin, B. I. Thermopower as a possible probe of non-Abelian quasiparticle statistics in fractional quantum Hall liquids. Phys. Rev. B 79, 115317 (2009).

    Article  ADS  Google Scholar 

  27. Cooper, N. R., Halperin, B. I. & Ruzin, I. M. Thermoelectric response of an interacting two-dimensional electron gas in a quantizing magnetic field. Phys. Rev. B 55, 2344–2359 (1997).

    Article  ADS  Google Scholar 

  28. Chickering, W. E., Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Thermoelectric response of fractional quantized Hall and reentrant insulating states in the N = 1 Landau level. Phys. Rev. B 87, 075302 (2013).

    Article  ADS  Google Scholar 

  29. Chickering, W. E., Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Thermopower of two-dimensional electrons at filling factors v = 3/2 and 5/2. Phys. Rev. B 81, 245319 (2010).

    Article  ADS  Google Scholar 

  30. Bolotin, K. I., Sikes, K. J., Hone, J., Stormer, H. L. & Kim, P. Temperature-dependent transport in suspended graphene. Phys. Rev. Lett. 101, 096802 (2008).

    Article  ADS  Google Scholar 

  31. Hwang, E. H. & Das Sarma, S. Acoustic phonon scattering limited carrier mobility in two-dimensional extrinsic graphene. Phys. Rev. B 77, 115449 (2008).

    Article  ADS  Google Scholar 

  32. Zuev, Y. M., Chang, W. & Kim, P. Thermoelectric and magnetothermoelectric transport measurements of graphene. Phys. Rev. Lett. 102, 096807 (2009).

    Article  ADS  Google Scholar 

  33. Wei, P., Bao, W., Pu, Y., Lau, C. N. & Shi, J. Anomalous thermoelectric transport of Dirac particles in graphene. Phys. Rev. Lett. 102, 166808 (2009).

    Article  ADS  Google Scholar 

  34. Kim, D., Syers, P., Butch, N. P., Paglione, J. & Fuhrer, M. S. Ambipolar surface state thermoelectric power of topological insulator Bi2Se3. Nano Lett. 14, 1701–1706 (2014).

    Article  ADS  Google Scholar 

  35. Checkelsky, J. G. & Ong, N. P. Thermopower and Nernst effect in graphene in a magnetic field. Phys. Rev. B 80, 081413 (2009).

    Article  ADS  Google Scholar 

  36. Hwang, E. H., Rossi, E. & Das Sarma, S. Theory of thermopower in two-dimensional graphene. Phys. Rev. B 80, 235415 (2009).

    Article  ADS  Google Scholar 

  37. Nam, S.-G., Ki, D.-K. & Lee, H.-J. Thermoelectric transport of massive Dirac fermions in bilayer graphene. Phys. Rev. B 82, 245416 (2010).

    Article  ADS  Google Scholar 

  38. Ghahari, F. et al. Enhanced thermoelectric power in graphene: violation of the Mott relation by inelastic scattering. Phys. Rev. Lett. 116, 136802 (2016).

    Article  ADS  Google Scholar 

  39. Small, J. P., Perez, K. M. & Kim, P. Modulation of thermoelectric power of individual carbon nanotubes. Phys. Rev. Lett. 91, 256801 (2003).

    Article  ADS  Google Scholar 

  40. Girvin, S. M. & Jonson, M. Inversion layer thermopower in high magnetic field. J. Phys. C: Solid State Phys. 15, L1147 (1982).

    Article  ADS  Google Scholar 

  41. Gallagher, B. L. et al. Observation of universal thermopower fluctuations. Phys. Rev. Lett. 64, 2058–2061 (1990).

    Article  ADS  Google Scholar 

  42. Sultana, N. et al. Replication data for: detection of fractional quantum Hall states by entropic sensitive measurements. George Mason University Dataverse https://doi.org/10.13021/orc2020/681UPS (2024).

  43. Oji, H. Thermopower and thermal conductivity in two-dimensional systems in a quantizing magnetic field. Phys. Rev. B 29, 3148–3152 (1984).

    Article  ADS  Google Scholar 

  44. Jonson, M. & Girvin, S. M. Thermoelectric effect in a weakly disordered inversion layer subject to a quantizing magnetic field. Phys. Rev. B 29, 1939–1946 (1984).

    Article  ADS  Google Scholar 

  45. Chickering, W. E. Thermopower in Two-Dimensional Electron Systems. PhD thesis, California Institute of Technology (2016).

  46. Esposito, F. P., Goodman, B. & Ma, M. Thermoelectric power fluctuations. Phys. Rev. B 36, 4507–4509 (1987).

    Article  ADS  Google Scholar 

  47. Ilani, S. et al. The microscopic nature of localization in the quantum Hall effect. Nature 427, 328 (2004).

    Article  ADS  Google Scholar 

  48. Huang, K. et al. Valley isospin controlled fractional quantum Hall states in bilayer graphene. Phys. Rev. X 12, 031019 (2022).

    Google Scholar 

  49. Hunt, B. M. et al. Direct measurement of discrete valley and orbital quantum numbers in bilayer graphene. Nat. Commun. 8, 948 (2017).

    Article  ADS  Google Scholar 

  50. Wu, Y.-H., Shi, T. & Jain, J. K. Non-Abelian parton fractional quantum Hall effect in multilayer graphene. Nano Lett. 17, 4643–4647 (2017).

    Article  ADS  Google Scholar 

  51. d’Ambrumenil, N., Halperin, B. I. & Morf, R. H. Model for dissipative conductance in fractional quantum Hall states. Phys. Rev. Lett. 106, 126804 (2011).

    Article  ADS  Google Scholar 

  52. Assouline, A. et al. Energy gap of the even-denominator fractional quantum Hall state in bilayer graphene. Phys. Rev. Lett. 132, 046603 (2024).

    Article  ADS  Google Scholar 

  53. Barlas, Y. & Yang, K. Thermopower of quantum Hall states in Corbino geometry as a measure of quasiparticle entropy. Phys. Rev. B 85, 195107 (2012).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank Y. Barlas and F. Mahfouzi for useful discussions. N.S. acknowledges funding from the National Science foundation (NSF) under award no. 2337497. F.G. thanks J. Schnur for inspiring discussions and support. F.G. acknowledges funding from the National Institute of Standards and Technology (NIST) under grant no. 70NANB23H012. T.T. and K.W. acknowledge support from the Japan Society for the Promotion of Science KAKENHI under grant nos. 21H05233 and 23H02052 and World Premier International Research Center Initiative (WPI), Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan. D.E.F. was supported in part by the NSF under grant no. DMR-2204635.

Author information

Authors and Affiliations

  1. Department of Physics and Astronomy, George Mason University, Fairfax, VA, USA

    Nishat Sultana, Robert W. Rienstra & Fereshte Ghahari

  2. Research Center for Electronic and Optical Materials, National Institute for Materials Science, Tsukuba, Japan

    Kenji Watanabe

  3. Research Center for Materials Nanoarchitectonics, National Institute for Materials Science, Tsukuba, Japan

    Takashi Taniguchi

  4. Physical Measurement Laboratory, National Institute of Standards and Technology, Gaithersburg, MD, USA

    Joseph A. Stroscio & Nikolai B. Zhitenev

  5. Theoretical Physics Center and Physics Department, Brown University, Providence, RI, USA

    D. E. Feldman

Authors
  1. Nishat Sultana
    View author publications

    Search author on:PubMed Google Scholar

  2. Robert W. Rienstra
    View author publications

    Search author on:PubMed Google Scholar

  3. Kenji Watanabe
    View author publications

    Search author on:PubMed Google Scholar

  4. Takashi Taniguchi
    View author publications

    Search author on:PubMed Google Scholar

  5. Joseph A. Stroscio
    View author publications

    Search author on:PubMed Google Scholar

  6. Nikolai B. Zhitenev
    View author publications

    Search author on:PubMed Google Scholar

  7. D. E. Feldman
    View author publications

    Search author on:PubMed Google Scholar

  8. Fereshte Ghahari
    View author publications

    Search author on:PubMed Google Scholar

Contributions

F.G. conceptualized and designed the experiment. N.S. fabricated the devices. N.S. performed measurements and analysed the experimental data, under the supervision of F.G. R.W.R. assisted with data acquisition and cryostat maintenance. D.E.F. provided theoretical support of the experimental data. T.T. and K.W. grew the hexagonal boron nitride crystals. F.G., J.A.S. and N.B.Z. wrote the paper with input from all co-authors.

Corresponding author

Correspondence to Fereshte Ghahari.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Thermopower measurements in the fractional quantum Hall regime in device no. 3.

a, The longitudinal thermal voltage Vxx (left axis) and Rxx (right axis) vs filling factor ν measured at B = 9 T and T = 1.64 K between pair 1 in device no. 3 (see e). While FQH states appear around filling factors 5/2 and 7/5 in Rxx, more FQH states are observable in Vxx. The temperature gradient was not calculated in this device due to a broken thermometer contact at base temperature. Therefore, the thermal voltage Vxx is plotted instead of thermopower. b, Landau fan of Vxx as a function of filling factor ν and magnetic field B at T = 300 mK measured between pair 1 in device no. 3 see e). In this plot the QH states appear as vertical lines at specific filling factors. In addition to integer QH states, FQH states at fractional fillings of 1/2, 4/5, 7/5, 5/2 and 8/3 are observable consistent with minima observed in a. c, Thermal voltage Vxx vs ν measured at B = −7.85 T and T = 300 mK between pair 2 in device no. 3 (see e). d, Landau fan of Vxx as a function of filling factor ν and magnetic field B measured at T = 300 mK between pair 2 showing vertical lines at fractional fillings including strong even denominator FQH states at 1/2 and 5/2 and odd denominator states consistent with those labeled in c. e, Optical image of a bilayer graphene thermopower device no. 3. Arrows show local thermometers and various electrode pairs used in measurements. f, Vxx and Vxy vs magnetic field B measured at fixed density of n = 0.99 × 1011 cm−2 at T = 300 mK between pair 1 showing a strong FQH state at ν = 5/2 specified by a minimum in Vxx (left axis) and a linear slope in Vxy (right axis) at this filling factor (see blue oval region). Only the strongest features are labeled.

Supplementary information

Supplementary Information

Supplementary Sections A–C, Figs. 1–21 and References.

Source data

Source Data Fig. 1

Source data for Fig. 1c,d,f.

Source Data Fig. 2

Source data for Fig. 2a–d,f,g.

Source Data Fig. 3

Source data for Fig. 3a–e.

Source Data Fig. 4

Source data for Fig. 4a,b.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sultana, N., Rienstra, R.W., Watanabe, K. et al. Detection of fractional quantum Hall states by entropy-sensitive measurements. Nat. Phys. 21, 724–731 (2025). https://doi.org/10.1038/s41567-025-02813-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-025-02813-z

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing