Abstract
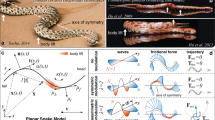
Snakes exhibit a wide variety of gaits, including gliding in air and sidewinding on land, which is particularly notable for its out-of-plane motion. Here we report the observation of another non-planar gait used as an escape strategy from threatening situations by juvenile anacondas (Eunectes notaeus), which we refer to as the S-start due to its shape. In this transient mode of locomotion, the snake writhes and bends out of the plane while rolling forward about its midsection without slippage. To quantify our observations, we develop a model for an active non-planar filament that interacts anisotropically with a frictional substrate. We demonstrate that locomotion is due to a propagating localized pulse of a topological quantity—the link density. A two-dimensional phase space characterized by scaled body weight and muscular torque shows that relatively light juveniles are capable of S-starts, whereas heavy adults are not, consistent with our experiments. We also show that a periodic sequence of S-starts naturally leads to a sidewinding gait.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon request. Source data are provided with this paper.
Code availability
Code used for the simulation is available via GitHub at https://github.com/Chelakkot/S-start.
References
Gray, J. Animal Locomotion (Norton,1968).
Marvi, H., Bridges, J. & Hu, D. Snakes mimic earthworms: propulsion using rectilinear travelling waves. J. R. Soc. Interface 10, 20130188 (2013).
Gray, J. & Lissmann, H. The kinetics of locomotion of the grass-snake. J. Exp. Biol. 26, 354–367 (1950).
Gasc, J., Cattaert, D., Chasserat, C. & Clarac, F. Propulsive action of a snake pushing against a single site: its combined analysis. J. Morphol. 201, 315–329 (1989).
Moon, B. & Gans, C. Kinematics, muscular activity and propulsion in gopher snakes. J. Exp. Biol. 201, 2669–2684 (1998).
Guo, Z. & Mahadevan, L. Limbless undulatory propulsion on land. Proc. Natl Acad. Sci. USA 105, 3179–3184 (2008).
Hu, D., Nirody, J., Scott, T. & Shelley, M. The mechanics of slithering locomotion. Proc. Natl Acad. Sci. USA 106, 10081–10085 (2009).
Alexander, R. Principles of Animal Locomotion (Princeton Univ. Press, 2013).
Biewener, A. & Patek, S. Animal Locomotion (Oxford Univ. Press, 2018).
Jayne, B. Kinematics of terrestrial snake locomotion. Copeia 1986, 915–927 (1986).
Gans, C. & Kim, H. Kinematic description of the sidewinding locomotion of four vipers. Isr. J. Zool. 38, 9–23 (1992).
Marvi, H. et al. Sidewinding with minimal slip: snake and robot ascent of sandy slopes. Science 346, 224–229 (2014).
Jayne, B. What defines different modes of snake locomotion? Integr. Comp. Biol. 60, 156–170 (2020).
Savidge, J., Seibert, T., Kastner, M. & Jayne, B. Lasso locomotion expands the climbing repertoire of snakes. Curr. Biol. 31, R7–R8 (2021).
Yeaton, I., Ross, S., Baumgardner, G. & Socha, J. Undulation enables gliding in flying snakes. Nat. Phys. 16, 974–982 (2020).
Fu, Q., Astley, H. & Li, C. Snakes combine vertical and lateral bending to traverse uneven terrain. Bioinspir. Biomim. 17, 036009 (2022).
Gart, S., Mitchel, T. & Li, C. Snakes partition their body to traverse large steps stably. J. Exp. Biol. 222, jeb185991 (2019).
Jayne, B. & Davis, J. Kinematics and performance capacity for the concertina locomotion of a snake (Coluber constrictor). J. Exp. Biol. 156, 539–556 (1991).
Alfaro, M. Forward attack modes of aquatic feeding garter snakes. Funct. Ecol. 16, 204–215 (2002).
Alfaro, M. Sweeping and striking: a kinematic study of the trunk during prey capture in three thamnophiine snakes. J. Exp. Biol. 206, 2381–2392 (2003).
Vincent, S., Herrel, A. & Irschick, D. Comparisons of aquatic versus terrestrial predatory strikes in the pitviper, Agkistrodon piscivorus. J. Exp. Zoo. A 303A, 476–488 (2005).
Alben, S. Efficient bending and lifting patterns in snake locomotion. Proc. R. Soc. A 478, 20220312 (2022).
Domenici, P. & Blake, R. The kinematics and performance of fish fast-start swimming. J. Exp. Biol. 200, 1165–1178 (1997).
Gazzola, M., Van Rees, W. & Koumoutsakos, P. C-start: optimal start of larval fish. J. Fluid Mech. 698, 5–18 (2012).
Kolinski, J., Aussillous, P. & Mahadevan, L. Shape and motion of a ruck in a rug. Phys. Rev. Lett. 103, 174302 (2009).
Rivas, J. et al. in Biology Of The Boas And Pythons (eds Henderson, R. W. & Powell, R.) 129–138 (Eagle Mountain Publishing, 2007).
Prange, H. & Christman, S. The allometrics of rattlesnake skeletons. Copeia 1976, 542–545 (1976).
Anderson, J., Rahn, H. & Prange, H. Scaling of supportive tissue mass. Q. Rev. Biol. 54, 139–148 (1979).
Garcia, G. & Silva, J. Interspecific allometry of bone dimensions: a review of the theoretical models. Phys. Life Rev. 3, 188–209 (2006).
O’Reilly, O. M. Modeling Nonlinear Problems in the Mechanics of Strings and Rods (Springer, 2017).
Gazzola, M., Dudte, L., McCormick, A. & Mahadevan, L. Forward and inverse problems in the mechanics of soft filaments. R. Soc. Open Sci. 5, 171628–171628 (2018).
Calugareanu, G. L’intégrale de Gauss et l’analyse des noeuds tridimensionnels. Rev. Math. Pures Appl. 4, 5–20 (1959).
Ricca, R. & Nipoti, B. Gauss’ linking number revisited. J. Knot Theory Ramif. 20, 1325–1343 (2011).
Fuller, F. The writhing number of a space curve. Proc. Natl Acad. Sci. USA 68, 815–819 (1971).
Tingle, J. Facultatively sidewinding snakes and the origins of locomotor specialization. Int. Comp. Bio. 60, 202–214 (2020).
Jayne, B. Muscular mechanisms of snake locomotion: an electromyographic study of lateral undulation of the Florida banded water snake (Nerodia fasciata) and the yellow rat snake (Elaphe obsoleta). J. Morphol. 197, 159–181 (1988).
Acknowledgements
We thank NSF grants BioMatter DMR 1922321, MRSEC DMR 2011754 and EFRI 1830901, the Simons Foundation and the Henri Seydoux Fund (L.M.) for partial financial support.
Author information
Authors and Affiliations
Contributions
B.Y. observed the escape behaviour and carried out the experiments with snakes. L.M. conceived and designed the study and approaches. N.C. performed the numerical simulations, in consultation with R.C., M.G. and L.M. L.M. conceived of the mathematical model, the phase space and the scaling laws. N.C., R.C. and L.M. wrote the paper. L.M. supervised the study.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Sections I–VII (describing the experimental methods, mathematical model and simulation parameters), Figs. 1–5, Tables I–III and refs. 1–11.
Supplementary Video 1
Experimental observations of S-start in baby yellow anacondas: we show the top-down and side-on views, slowed down by a factor of 25×. In real time, one cycle of the S-start takes approximately 0.5 s.
Supplementary Video 2
Simulations of the S-start and friction-dominated and inertia-dominated snake gaits: these correspond to the phases depicted in Fig. 3b. The red snake surface indicates contact with the ground, whereas yellow indicates a lifted portion of the snake body. Snake contact with the ground is marked by a grey trace left on the ground, showing that the central contact point traces an approximately straight path. Simulation parameters are listed in Supplementary Tables II and III, except that we use length L = 1.4 m and maintain diameter a = 0.04 m. We increased the length of this video to prolong the S-start process to allow for better visualization. All the parameters except lifting torque and mass density remain constant between simulations of the three locomotion modes. Lifting torque for friction-dominated motion corresponds to Γ = 6.3 × 103 Pa; for the S-start, lifting corresponds to Γ = 9.4 × 104 Pa, and for inertia-dominated, to Γ = 1.9 × 104 Pa. Mass density for friction-dominated motion corresponds to ρ = 800 kg m–3; for the S-start, ρ = 460 kg m–3; and for inertia-dominated motion, ρ = 80 kg m–3. Note that the values used for Γ and ρ in each type of locomotion are within an order of magnitude of what would be expected experimentally based on the results of Supplementary ref. (10). We vary them from this expected value to produce different forms of locomotion. Note that it is the dimensionless ratio \(R=\frac{{\rho} {g}\,{L}^{2}}{{\varGamma} {a}}\) that determines the type of locomotion (Fig. 3a). Computing this ratio for each simulation shown in this video, we get Rfriction = 61, RS = 23 and Rinertia = 20. As expected, Rfriction < RS < Rinertia. Note that Rinertia falls in the lower half of the S-start regime (Fig. 3a) rather than in the inertia-dominated regime; this may be due to the fact that a/L is smaller here than in the simulations used for Fig. 3a.
Supplementary Video 3
Experimental and simulated sidewinding motion: experiments are obtained from ref. 12, which can be found at https://science.sciencemag.org/content/suppl/2014/10/08/346.6206.224.DC1. Simulation procedures are described in Supplementary Section V. As shown in Supplementary Video 2, the red snake surface indicates contact with the ground, whereas yellow indicates a lifted region. Contact with ground is marked by a grey trace left on the ground, showing the parallel straight paths traced by the contact points of successive torque wave triplets. The simulation settings are described in Supplementary Tables II and III. For comparison to the S-start, the dimensionless ratio R = ρgL2/Γa is Rsidewinding = 16.7.
Supplementary Video 4
Experimental observation of S-start in baby anaconda in real time: we show the top-down view of S-start in real time.
Source data
Source Data Fig. 1
Unprocessed, compressed image files used in Fig. 1.
Source Data Fig. 2
Compressed data files for Fig. 2.
Source Data Fig. 3
Compressed data files for Fig. 3.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Charles, N., Chelakkot, R., Gazzola, M. et al. Topological dynamics of rapid non-planar gaits in slithering snakes. Nat. Phys. 21, 856–860 (2025). https://doi.org/10.1038/s41567-025-02835-7
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41567-025-02835-7
This article is cited by
-
Moonwalking baby anacondas provide blueprint for flexible robots
Nature India (2025)
-
Anacondas get vertical on the ground
Nature Physics (2025)