Abstract
Recent experiments on magic-angle twisted bilayer graphene have shown the formation of flat bands, suggesting that electronic correlation effects are likely to dominate in this material. However, a global transport measurement showing distinct signatures of strong correlations—such as local moments arising from the flat bands—is missing. Here we demonstrate the presence of emergent local moments through their impact on entropy extracted from thermopower measurements. In addition to sign changes in the thermopower at the Dirac point and full filling of the flat bands, we observe sign changes near the quarter-filled bands that do not vary with temperature from 5 K to 60 K. This is in contrast to temperature-dependent crossing points seen in our study on twisted bilayer graphene devices with weaker correlations. Furthermore, we find that applying a magnetic field reduces the thermopower, consistent with spin entropy suppression observed in layered oxides under partial spin polarization. Neither the robust crossing points nor the suppression by a magnetic field can be explained solely from the contributions of band fermions; instead, our data suggest a dominant contribution coming from the entropy of the emergent localized moments of a strongly correlated flat band.
Similar content being viewed by others
Main
The introduction of a relative twist angle between two or more van der Waals layers, resulting in the formation of a moiré superlattice, has opened a new field of exploration in condensed matter research, termed twistronics1,2,3,4. Within the family of twisted heterostructures, the magic-angle twisted bilayer graphene (MATBLG) with a twist angle (θM ≈ 1.1°) is extensively studied1,2,3,5,6,7,8,9,10. The interlayer hybridization between the rotated monolayers of MATBLG plays a crucial role in forming isolated flat bands, resulting in the effective electronic kinetic energy being substantially smaller than the effective Coulomb interactions, thus enabling the realization of a rich phase diagram dominated by strong correlations1,11,12,13. Emergent phenomena such as superconductivity2,3,14,15,16, correlated Mott insulators1,3, Coulomb blockade in scanning tunnelling microscopy (STM)11,12,13,17, orbital ferromagnetism18,19, anomalous Hall effects20, quantized anomalous Hall effects21, nematicity15, Chern insulators5,6,22, strange metals23, the Pomeranchuk effect24,25 and giant thermopower26 at low temperatures have been reported. These experimental features show a combination of properties: some are associated with itinerant electrons, while others relate to atomic orbital physics with localized moments.
To elucidate these experimental observations, a comprehensive framework of heavy fermion physics has been invoked27,28,29,30,31. In this framework, the more dispersive c-band and the flat f-band hybridize to form the emergent band of MATBLG with narrow bandwidth. In addition to the normalized bands, we expect that the flat band of MATBLG would lead to the formation of emergent local moments due to strong correlations, with orbital, valley and spin characteristics. Although thermodynamic probes such as compressibility measurements24,25 have indicated the presence of local moment fluctuations in MATBLG, and STM studies9,11,12,13,17 suggest that strong correlations dominate in MATBLG (one of the key ingredients for exhibiting local moments), a global transport measurement is still lacking to conclusively establish the presence of emergent local moments in MATBLG. Recent experiments on twisted bilayer32 and twisted trilayer graphene33 using photothermoelectric effects have turned to heavy fermion theory34 to interpret the observed results, primarily originating from the lighter c-electrons, as opposed to f-electrons with a much shorter lifetime. In this work, we use thermopower—a global transport probe to measure a system’s entropy—to study the presence of emergent local moments due to strong correlations in the flat band of MATBLG. We believe this is a crucial step in understanding thermopower and its dichotomy with electrical transport.
We have conducted comprehensive thermopower studies, varying the filling factor (ν) and temperature (T), on two types of twisted bilayer graphene (TBLG)-based devices: (1) type 1, MATBLG device with expected U/W ≳ 1, and (2) type 2, TBLG devices with expected U/W ≲ 1, where U and W represent the interaction strength and bandwidth, respectively. Except for low temperatures (T < 7 K), the thermoelectric voltage (VTh) of the MATBLG for both the conduction and valence bands remains symmetric with respect to the Dirac point (DP) with opposite signs. Aside from the anticipated sign changes in VTh at the DP (ν = 0) and full band filling (ν = ±4), additional sign changes or crossing occur around ν ≈ ±1. Our key observations are as follows:
-
(1)
The positions of the three crossing points (at the DP and the additional crossing points, νcross ≈ ±1) remain constant from T ≈ 5 K to 60 K for MATBLG with U/W ≳ 1. This is in contrast to the temperature-sensitive behaviour of the three crossing points for TBLG devices with U/W ≲ 1, for which three crossings merge into a single one around 30 K.
-
(2)
Using non-interacting band electrons and weak coupling interactions with Hartree–Fock (HF), we find that theoretical models based on the single-particle picture predict that the additional crossing points (νcross) are highly temperature dependent and fail to capture the robustness of these crossings observed experimentally for MATBLG.
-
(3)
Our theoretical models, based on dynamical mean-field theory (DMFT) and a minimal model of the atomic limit with strong correlation (W ≲ U), successfully capture the robustness of the additional crossing points νcross to temperature changes.
To validate the presence of a strong correlation, we investigate the effect of a magnetic field (B) on VTh for MATBLG. We find that, with B∥ and B⊥, VTh shows a 30% and 50% reduction, respectively, with minimal change in resistance. The response to the magnetic field, along with the robust νcross, suggests that VTh in MATBLG arises predominantly from the emergent local moment degrees of freedom (spin/valley), highlighting the importance of strong correlations in flat bands.
Thermopower of band versus strongly correlated electrons
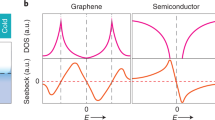
Figure 1b illustrates a schematic of TBLG featuring AA and AB stacking regions. The f-electrons localize at the AA sites27,29,34,35,36,37, while c-electrons move primarily through the AB regions35,36,37, as depicted in the schematic. These f- and c-electrons hybridize, resulting in the normalized flat band of MATBLG. In the strongly correlated regime (W ≲ U) of a flat band, the thermopower (Sth) and the total entropy (Sen) are related by the Heikes limit38,39 (\({S}_{{\mathrm{th}}}=-\frac{1}{e}\times \frac{\partial {S}_{{\mathrm{en}}}}{\partial N}\)), where N is the total number of particles and e is the electronic charge. The entropy can be considered a combination of configurational (Sconf) and spin (Sspin) contributions38. The Sconf can be envisioned as follows: because the AA sites contain approximately 95% of the carriers29,36, at any filling (ν < ±4), the Sconf represents the number of ways the AA sites can be filled with carriers (Fig. 1b), and its behaviour with ν is illustrated in Fig. 1d (top) for two regimes, kBT < U (blue line) and kBT > U (red line), where kB is the Boltzmann constant. The Sspin arises from the local moment’s degrees of freedom (spin/valley). The corresponding thermopower38,40 is depicted in Fig. 1d (bottom). As long as kBT < U, thermopower exhibits additional sign changes around ν ≈ ±1.3.
a, Schematic of the measurement set-up. The devices comprise hBN-encapsulated TBLG on a Si/SiO2 substrate. For the VTh measurement, an isolated gold heater line (H) is positioned parallel to one side of the stack. Passing a current in heater line (Ih) raises the temperature of the source contact (S), while the drain contact (D) is kept fixed at bath temperature via cold ground (CG). Bottom inset: the side view of the heterostructure. b, A schematic of TBLG with AA and AB stacking regions. In the strongly correlated regime, the majority of the carriers are localized at the AA sites with local moments as indicated by the black arrow, while the mobile itinerant carriers move primarily through the AB regions as indicated by the blue lines. At a given partial filling, ν, some sites are occupied (yellow filled regions) while others remain empty (grey regions), and various ways to occupy the AA sites give rise to the dominant contribution to the thermopower via configurational entropy together with the local moment’s degrees of freedom (spin/valley character). c, By contrast, the contribution of thermopower from the non-interacting band electrons arises from the particle–hole asymmetry of a band. Top: the effective DOS (∫g(ε)(−df/dε)dε) due to thermal broadening, where g(ε) is the DOS. Bottom: the expected thermopower from band electrons using the semi-classical equation at different temperatures. d, Top: the entropy per unit moiré unit cell (\({S}_{{\mathrm{en}}}^{{\mathrm{M}}}\)) from the atomic limit with ν for kBT > U and kBT < U, where U is the onsite Coulomb repulsion. Bottom: the thermopower, \({S}_{{\mathrm{th}}}=-\frac{1}{e}\times \frac{\partial {S}_{{\mathrm{en}}}^{{\mathrm{M}}}}{\partial \nu }\) with ν.
In the regime where U ≈ 0, the thermopower of a flat band can be represented by non-interacting band electrons, for which Sth is expected to be proportional to the derivative of the density of states (DOS), g(ε). However, as temperature increases, one must consider the impact of the effective DOS (∫g(ε)(−df/dε)dε) due to thermal broadening. This effect is represented by the blue and red lines in Fig. 1c (top) for 5 K and 50 K, respectively. The calculated thermopower using a semi-classical description with a DOS following the continuum model is displayed in Fig. 1c (bottom) and is highly sensitive to temperature. If thermal broadening becomes comparable to half of the bandwidth (3.5kBT ≈ W/2), the additional sign changes merge with the DP.
Device and measurement set-up
Figure 1a illustrates the schematic of our thermopower measurement set-up. The devices comprise hexagonal boron nitride (hBN)-encapsulated TBLG with Si/SiO2 or graphite back-gated. Further details are provided in Supplementary Section 1 and Methods. For the thermopower measurement, an isolated gold heater line, depicted in Fig. 1a, is positioned parallel to one side of the stack. The thermoelectric voltage, VTh, measurement uses a well-established 2ω lock-in technique at ω = 7 Hz (refs. 41,42,43,44,45,46,47) in linear regime (Supplementary Section 2), whereas we have used Johnson noise thermometry26 to measure the temperature difference (ΔT) to extract the thermopower (Supplementary Fig. 5). However, except low temperatures (below 10 K), we have only concentrated on the thermoelectric voltage, VTh, because extracting ΔT using noise thermometry is challenging at elevated temperatures owing to high background equilibrium thermal noise. We have carried out measurements on four devices: MATBLG (1.05°), near MATBLG (0.95°), twisted double bilayer graphene (TDBLG around 1.1°) with SiO2 back-gate and approximately 1.2° TBLG with graphite back-gate. The advantages of our geometry (Fig. 1a and Supplementary Section 1) are discussed in Supplementary Section 2, and further details can be found in our previous work26,48, where VTh is investigated at lower temperatures, specifically below 10 K.
In the upcoming sections, we discuss our measurements of the temperature-dependent evolution of the thermoelectric voltage (VTh). We explore different temperature ranges in relation to the key energy scales of the system, including the bandwidth (W) of the flat band, the interaction strength (U) and the energy gap between the dispersive lower and upper bands (Δg). We compare the results from two types of device: (1) U/W ≳ 1 − SiO2 back-gated 1.05° MATBLG and (2) U/W ≲ 1 − 1.1° TDBLG and 1.2° TBLG with graphite gating. This categorization is based on their resistance response to filling and temperature, as well as their distinct thermopower responses. The stronger correlation in SiO2 back-gated MATBLG is indicated by the more pronounced resistance peaks at integer fillings, which persist beyond 100 K, in contrast to the weaker resistance peaks in graphite-gated TBLG, which vanish within 50 K (Figs. 2 and 5 and Supplementary Fig. 9). This is further supported by experimentally determined typical energy scales for the SiO2 back-gated MATBLG (via STM12), which are approximately W ≈ 20 meV, U ≈ 20–30 meV (refs. 9,12) and Δg ≈ 30–40 meV (ref. 1), suggesting that SiO2 back-gated MATBLG devices are in the strong correlation regime.
a, R as a function of ν plotted for several T. For visual clarity, each dataset is offset by 10 KΩ along the y axis with increasing T. In general, R(T) shows metallic behaviour except at the DP (ν = 0), and at ν = ±4 when the bands are fully filled, where R(T) shows insulating behaviour. Additional peaks in R(ν) emerge at positive integer filling (ν = 1, 2 or 3), that is, for the conduction band, but are weaker for the valence band. b, VTh(ν) for several T with an offset of 10 μV. VTh is symmetric for the conduction and valence bands with opposite signs (except at 6 K), which is in stark contrast to the asymmetry of resistance data. The sign of VTh changes at DP and ν = ±4 with additional points at νcross ≈ ±1. It is important to note that the location of νcross barely changes with increasing T. c, Non-interacting single-particle DOS of flat bands using a continuum model10 with the inclusion of parabolic dispersive bands5. d, Thermopower in shifted plot calculated semi-classically (SSC) using the DOS in c. Note that, at low T, SSC shows crossing between 0 < ∣ν∣ < 4, which is strongly dependent on T and vanishes beyond 18 K. SSC at higher T becomes positive (negative) for the conduction (valence) band caused by the thermal broadening (−df/dε).
Anomalous thermopower response of MATBLG at low temperature
In this section, we showcase the data within a temperature range that is both lesser and comparable to W, yet lower than U and Δg. In Fig. 2a, the resistance (R) as a function of filling (ν) is plotted for several temperatures (T) between 6 K and 50 K. The ν = 4n/ns is the moiré filling factor, where n and ns are the carrier density induced by the gate voltage and the carrier density required to fully fill the flat band (four electrons/holes per moiré unit cell), respectively. Insulating resistance peaks can be observed at the DP (ν = 0) as well as the band full-filling points (ν = ±4). Additional prominent peaks emerge at positive integer filling (ν = 1, 2 or 3), that is, for the conduction band, which survives even up to 100 K. By contrast, such peak features at integer filling remain very weak for the valence band.
In Fig. 2b, thermoelectric voltage (VTh) with ν is plotted for same T values between 6 K and 50 K. VTh shows sign changes at the primary DP and full-filling points. In addition, we observe sign changes near ν ≈ ±0.95. It is to be noted that the position of the crossing point at ν ≈ ±0.95 barely evolves with increasing T from 5 K to 50 K, which is an order-of-magnitude change in temperature. At low temperatures, a peak in VTh appears around ν = 2. However, at temperatures above 8 K, VTh appears very symmetric between the valence and conduction band with opposite signs, which is in stark contrast to the asymmetric nature of the resistance data in Fig. 2a. Specifically, VTh violates the Mott relation49 (dlnR/dν) at integer fillings, as depicted later in the paper as well as Supplementary Fig. 27. The dlnR/dν, according to Mott’s description of thermopower49, anticipates sign changes at resistance peaks and dips, shown in Fig. 5c and illustrated by the blue curves in Supplementary Fig. 27. Even up to T ≈ 90 K, six sign changes are observed for the conduction band, distinct from the sign changes at the DP and band full filling. This is in stark contrast to the measured VTh data shown in Fig. 2b. The Mott relation is violated in all our devices within certain density and temperature ranges, as shown in Supplementary Section 15. Various possible origins for this violation are discussed in Supplementary Section 16. Among these, the presence of interaction is one of the origins; however, it does not alone elucidate the physics of local moments.
To get a sense of the effect of the band on temperature-dependent VTh (non-interacting), we have calculated the thermopower using a semi-classical approach (details in Methods and Supplementary Section 8). The non-interacting single-particle DOS of the flat band calculated using the continuum model10 (W ≈ 10 meV) with the inclusion of parabolic dispersing5 lower and upper bands is shown in Fig. 2c. Semi-classically, the thermopower can be approximated as follows: SSC = −(1/Te)[∫(ϵ − μ)g(ε)(−df/dε)dε]/[∫g(ε)(−df/dε)dε], where e, T, μ, g(ε) and −df/dε are, respectively, the electronic charge, temperature, chemical potential, DOS and derivative of Fermi function. SSC has been calculated with self-consistently solved μ. At low temperatures, SSC also shows a crossing between 0 < ∣ν∣ < 4, which is strongly tunable with T and vanishes beyond 18 K as shown in Fig. 2d. At elevated temperatures, SSC transitions to positive (negative) values for the conduction (valence) band. This arises due to thermal broadening (full width at half maximum of −df/dε ≈ 3.5kBT), treating the flat bands as a single band, and the charge neutrality point behaves resembling a transition point from electron to hole-like for a half-filled single band. In Supplementary Section 8, calculations were further extended to varying bandwidths up to 40 meV and using different types of DOS, from continuum to saw-tooth. The results show that the crossing points in thermopower from non-interacting band electrons are highly sensitive to temperature, although the merging to a single crossing point depends on the magnitude of the bandwidth. Moreover, calculations were performed in the presence of interaction in the weak-coupling regime using HF, as shown in Supplementary Fig. 16, and the outcome remains similar to that of non-interacting band electrons. Comparing Fig. 2b with Fig. 2d, it is evident that single-particle band electrons fail to capture the measured VTh. In the next section, we will discuss how thermopower from local moments qualitatively captures our experimental data.
Local moment versus experimental thermopower
To capture the effect of correlation, we have considered various theoretical models (Supplementary Sections 10 and 11) with increasing correlation effects. Among these, the DMFT at intermediate interaction strength U/W ≲ 1 captures the robust crossing in thermopower as shown in Fig. 3e and Supplementary Fig. 17. To see the effect of strong correlation50 in thermopower, we use a minimal model of atomic limit, the limiting case of extremely strong interaction and the bandwidth approaching zero, t ≪ kBT ≪ U. In the atomic limit, the thermopower is known as Heikes limit38,39 (\({S}_{{\mathrm{th}}}=-\frac{1}{e}\times \frac{\partial {S}_{{\mathrm{en}}}^{{\mathrm{M}}}}{\partial \nu }\), where \({S}_{{\mathrm{en}}}^{{\mathrm{M}}}\) is the entropy per moiré unit cell) and further can be derived from the Kelvin formula40 (details in Supplementary Section 11). In the regime of strong correlation, a reduction in entropy occurs when the band is half-filled (with four out of eight orbitals filled), as depicted by the blue line in Fig. 1d (top). This reduction leads to additional crossing points in the thermopower at νcross ≈ ±1.3, as observed in our theoretical calculations for U = 20 meV (ref. 12) shown in Fig. 3a. The temperature independence of the crossing points in the atomic limit for varying U from 15 to 40 meV is demonstrated in Supplementary Fig. 19c. To incorporate finite hopping in our calculation, thermopower is computed using exact diagonalization for a small cluster of moiré sites via the Kelvin formula, showing the robust crossing (Supplementary Fig. 22). As shown below, among the various theoretical models, the simplest minimal model of atomic limit explains the most striking features of our experiment.
a, Theoretically calculated thermopower in a strongly correlated regime using the atomic limit38,39,40 at different temperatures with U = 20 meV. The additional crossings, νcross around ±1.3, are indicated by vertical black arrows. b, The extracted νcross from Fig. 3a as a function of temperature is shown in a solid violet line. For contrast, νcross from non-interacting band electrons using semi-classical theory (for W ≈ 10 meV) is shown by a black line. c, Evolution of the crossing points (within 0 < ∣ν∣ < 4) with T for MATBLG (red circles) and near MATBLG (blue triangles). Note that, for the strongly correlated MATBLG with flatter bands, νcross remains almost constant, resembling the thermopower from the local moments in Fig. 3b. However, for the near MATBLG device with bands that are not as flat, there is greater variation in νcross. d, TDBLG with weaker correlation exhibits notable νcross variations with T: in the valence band, νcross shifts to lower ν and disappears by 20 K, while in the conduction band, νcross approaches ν = 0 around 35 K and qualitatively resembles the solid black line that is non-interacting band electrons in b. e, The temperature evolution of the crossing points of thermopower calculated using DMFT for U, W = 6, 10 meV (blue), U, W = 12, 20 meV (black) and U, W = 20, 20 meV (red) contrasted with crossing points evolution for HF thermopower at U, W = 12, 20 meV (green). Even DMFT with U ≲ W (blue plot) has only weak temperature dependence over a broad range, unlike the HF thermopower, where the crossing point varies significantly with temperature and merges to a single crossing point at much lower temperature.
The solid violet line in Fig. 3b illustrates the evolution of νcross with temperature, for thermopower from strong correlations using atomic limit in comparison with the non-interacting band electrons, SSC (solid black line). Figure 3b highlights that νcross from the strong correlations or local moments remains nearly constant, contrasting with νcross from band electrons, which are sensitive to temperature. In Fig. 3c, the evolution of experimentally measured νcross within 0 < ∣ν∣ < 4 is presented for MATBLG (red circles) and near MATBLG (blue triangles) devices, while Fig. 3d shows the results for TDBLG and shown for graphite-gated TBLG in Supplementary Fig. 9b. Comparing Fig. 3b with Fig. 3c and Supplementary Fig. 9b, the MATBLG device closely resembles atomic limit physics with strong correlation, a trend also observed for the near MATBLG device, albeit with some variation (possibly arising from the larger bandwidth and effect from the higher-dispersive band). However, the TDBLG and graphite-gated TBLG devices qualitatively align closely with the thermopower from single-particle band electrons (or weaker correlation effect), which is not unexpected, considering that for TDBLG with 1.1°, correlation effects are weaker at zero displacement field as well as expected for the screened TBLG device. The raw data of VTh related to all the devices are shown in Supplementary Section 3. The DMFT results and the HF calculations are shown in Fig. 3e (see Supplementary Section 10 for details).
Note that an effective model of flat bands for MATBLG51,52 requires a multiorbital SU(8) description to account for Hubbard interactions involving spin, valley and band quantum numbers. This model predicts multiple additional crossings in thermopower (Supplementary Fig. 21), which are absent in experiments. By contrast, the minimal SU(2) atomic-limit model best captures the observed crossing points at ν ≈ ±1. DMFT and exact diagonalization calculations on a small cluster of moiré sites, incorporating finite hopping, closely match experimental data. These calculations corroborate the connection between strongly correlated local moment regimes in the extreme atomic SU(2) limit and away from strictly atomic limit of SU(8) with finite bandwidth effects. The finite energy dispersion of MATBLG flat bands, along with intrinsic and extrinsic symmetry breaking, is expected to reduce the large SU(8) symmetry of the atomic limit to lower-symmetry groups28,29,34,51,52. For a detailed discussion, see the ‘Atomic limit with multi-orbitals’ section in Supplementary Section 11.
Magnetic field dependence of thermopower
Figure 4a (top) shows VTh with ν for different B∥ at 25 K. Here, the VTh at a given field is normalized to B∥ = 0T. With increasing B∥, in the range between a quarter (∣ν∣ = 1) and full (∣ν∣ = 4) filling of both valence and conduction band, a clear decrease of VTh is observed. The effect is more pronounced in the valence band and quantified by plotting its relative magnitude with B∥ in Fig. 4a (bottom) for ν = −3.2, and 30% reduction can be seen. The reduction in VTh with B∥ is in stark contrast to the resistance response (Supplementary Fig. 10b), where no noticeable change in R with B∥ can be observed. Figure 4b (top) illustrates the evolution of normalized VTh with B⊥ at 20 K. In contrast to B∥, a more substantial decrease in the VTh signal is observed with increasing B⊥, quantified in Fig. 4b (bottom) for ν = −3.5, where a 50% reduction is evident. It is worth noting that, at 20 K, no clear signature of Landau level formation was observed with B⊥ in the resistance data (Supplementary Fig. 10f). In addition, Landau levels are expected to exhibit oscillations in VTh (ref. 53), which is not seen in Fig. 4b owing to thermal broadening except for a weak modulation near DP. Similarly, no signature of the Hofstadter-butterfly effect54 was seen in our data at 20 K. The reduction in VTh with B may be arising due to partial polarization of spin/valley degrees of freedom. However, further experiments (with temperature, comparing the response with screened versus unscreened devices) and theoretical exploration are needed to understand the influence of the magnetic field on thermopower and its connection with local moments. In Fig. 4c, we have plotted the integral of VTh to ν to see how the relative magnitude of entropy (Sen) reduces with increasing magnetic field. One can notice that the shape of Fig. 4c resembles the theoretically calculated entropy from the atomic limit in Fig. 4d (details in Supplementary Fig. 19). The study with the magnetic field is performed with a fixed heater current, keeping other parameters fixed. The measurements are done at a constant ΔT (as in ref. 26); hence, the relative change in VTh is expected to be the same as in the thermopower. The exact magnitude of the entropy is shown in Supplementary Fig. 25 at 6 K in units of kB/moiré, and an estimation is shown for 20 K.
a, Top: VTh with ν for different B∥ at 25 K. Here the VTh is normalized to VTh measured at B∥ = 0T. Bottom: the reduction of VTh can be observed with increasing B∥, and the effect is more pronounced for the valence band and plotted at ν = −3.2 (vertical black arrow), which shows 30% reduction. b, Top: the evolution of normalized VTh with B⊥ at 20 K. Bottom: in contrast to B∥, a larger decrease of the VTh signal is observed with increasing B⊥ and plotted for ν = −3.55 (vertical black arrow), where 50% reduction can be seen. c, Normalized entropy estimated from the integral of the VTh with ν at 20 K from B⊥ data. The peak position of the entropy saturates to ν ≈ ±1.3 (vertical dashed black lines) with higher B⊥. d, Theoretical entropy calculated using atomic limit for zero magnetic field. The shape of the experimental entropy in c resembles the theoretical entropy of local moments.
High-temperature response of thermopower of MATBLG
After discussing the VTh in the intermediate temperature (5–60 K), in this section, we present the results for a higher temperature range of 70–300 K, such that we can study VTh for the non-interactive regime (kBT ≳ U) as well as the effect of upper and lower dispersive bands (kBT ≳ Δg).
Figure 5a illustrates the evolution of R with T in the range of 70–300 K as a function of ν. At 70 K, flat-band features persist, evident in resistance peaks at ν = ±4 and kinks at integer values. The asymmetry between valence and conduction bands is noticeable. As temperature increases beyond 120 K, flat-band features fade, and the resistance spectrum resembles a graphene-like behaviour with a single Dirac peak at the charge neutrality point. The spectrum becomes more symmetric with rising temperature. In Fig. 5b, the evolution of VTh with T is depicted for ν in the range of 70–300 K. Above 70 K, no crossings occur inside the flat band, except at the DP. Between 80 K and 120 K, VTh remains nearly flat and close to zero within ∣ν∣ ≈ 2. Beyond 120 K, the response of VTh is consistently negative (positive) throughout the conduction (valence) band, akin to the thermopower response observed in graphene41,46,55. The comparison between the measured VTh and derivative of resistance (dlnR/dν) of MATBLG versus ν is shown in Fig. 5c, and details can be found in Supplementary Section 15. Beyond 120 K, VTh starts to fall in good agreement with Mott, as evident in Fig. 5c (bottom).
a, The evolution of R with ν for T in the range 70–300 K. Beyond 100 K, the flat-band features fade and show a graphene-like resistance spectrum. b, The evolution of VTh with ν within the temperature range 70–300 K. For T within 80–100 K, the VTh remains flat and close to zero within the doping range ∣ν∣ ≈ 2. For T beyond 120 K, VTh remains negative (positive) throughout the conduction (valence) band, similar to graphene. c, Validation of Mott, measured VTh and derivative of resistance (dlnR/dν) of MATBLG at several T. The dlnR/dν in light-blue lines and VTh in orange curves. The violation of the Mott formula persists up to 120 K, beyond which VTh starts to fall in good agreement with Mott, as evident from 200 K and 300 K data.
In this paragraph, we summarize the observed thermopower across different temperature ranges. As previously mentioned, the key energy scales include the bandwidth (W) of the flat band, the strength of interaction (U) and the energy gap (Δg) between the dispersing lower and upper bands (illustrated schematically in Supplementary Fig. 23). (1) When W < U < Δg < kBT, the contributions from higher-dispersing bands dominate, resulting in positive thermopower for ν < 0 and negative for ν > 0 at high temperatures, as depicted for T > 120 K in Fig. 5b. This behaviour is characteristic of graphene-based systems due to electron–hole symmetry, which manifests as a crossing at ν = 0 (DP). (2) When W < U < kBT ≈ Δg, the effect of the flat band starts contributing along with higher-dispersing bands. However, these contributions exhibit opposite signs, leading to nearly flat, close-to-zero VTh, as observed for T within 80–120 K in Fig. 5b. (3) In the scenario where W < U ≈ kBT < Δg, the influence of the flat band dominates, overshadowing contributions from higher-dispersing bands. This regime, illustrated by the solid red line in Fig. 1d (bottom), with single crossing at ν = 0 with positive values for ν > 0 and negative for ν < 0. This behaviour is observed within a narrow temperature range around 70 K, as depicted in Fig. 5b. (4) When W ≤ kBT ≤ U, the strong correlation starts to dominate, leading to three prominent crossings (ν = 0, ν ± 1), as illustrated in Fig. 2b. Supplementary Fig. 24 provides a pictorial summary of the thermopower response of MATBLG across various temperature ranges, comparing it with theoretical expectations.
Conclusion
In summary, our thermopower response is consistent with the effects of strong correlations in MATBLG. However, there are still puzzles that require an understanding of orbital and valley effects to gain a clearer picture of the system and to design novel methods to differentiate these contributions. Such insights will pave the way for the future development of thermoelectric devices that harness the unique characteristics of flat bands in twisted heterostructures.
Methods
Device fabrication and measurement scheme
We have used the modified ‘tear and stack’ technique to fabricate the twisted heterostructures, and details are mentioned in Supplementary Information. We have used four devices: three of them are controlled by Si/SiO2 gating, whereas the graphite gating controls one TBLG device. All the contacts are made of Cr (2 nm), Pd (10 nm) and Au (70 nm). For all the devices, the heater line, which is electrically isolated from the devices, is used to create the temperature gradient. The thermoelectric voltage is measured using standard V2ω technique, and the temperature gradient is measured using Johnson noise thermometry. The details can be found in Supplementary Information.
Semi-classical calculation
The semi-classical description of Boltzmann theory to calculate thermopower for the band electrons is given by the following relation considering energy-independent relaxation approximation:
where g(ϵ) refers to the DOS as a function of energy (ϵ), f is the Fermi function, e is being the electronic charge and μ is the chemical potential. Note that, in equation (1), df/dϵ has a finite width beyond which df/dϵ → 0, thus eliminating the necessity to integrate over −∞ < ϵ < ∞. For all practical purposes, integral over the low-energy flat band and some portion of the dispersive band accurately depicts the semi-classical behaviour of thermopower. The self-consistently solved μ is used to calculate the thermopower. The details can be found in Supplementary Section 8.
Thermopower from atomic limit
In this regime, the flat bands and interactions therein are expected to dominate. We work in the atomic limit where Hamiltonian is given by \(H={\sum }_{\alpha }\left(U{n}_{\alpha \uparrow }{n}_{\alpha \downarrow }+{\epsilon }_{\alpha }{n}_{\alpha }\right)\) where α = {1, …, 4} labels the four orbitals and U is the Hubbard interaction. Evaluating the partition function Z and the corresponding Helmholtz free energy is given by F = −kBTlogZ and the corresponding entropy is given by \({S}_{{\mathrm{en}}}=-\left(\frac{\partial F}{\partial T}\right)\). The thermopower is then given by \({S}_{{\mathrm{th}}}=-\frac{1}{e}\frac{\partial {S}_{{\mathrm{en}}}}{\partial \nu }\) where e is the electric charge. It should be noted that μ is solved self-consistently to fix the filling ν. The details are described in Supplementary Section 11.
Data availability
The data presented in the article are available from the corresponding author upon request. Source data are provided with this paper.
References
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653–657 (2019).
Liu, X. et al. Tunable spin-polarized correlated states in twisted double bilayer graphene. Nature 583, 221–225 (2020).
Das, I. et al. Symmetry-broken Chern insulators and Rashba-like Landau-level crossings in magic-angle bilayer graphene. Nat. Phys. 17, 710–714 (2021).
Nuckolls, K. P. et al. Strongly correlated Chern insulators in magic-angle twisted bilayer graphene. Nature 588, 610–615 (2020).
Stepanov, P. et al. Untying the insulating and superconducting orders in magic-angle graphene. Nature 583, 375–378 (2020).
Liu, X. et al. Tuning electron correlation in magic-angle twisted bilayer graphene using Coulomb screening. Science 371, 1261–1265 (2021).
Wong, D. et al. Cascade of electronic transitions in magic-angle twisted bilayer graphene. Nature 582, 198–202 (2020).
Zondiner, U. et al. Cascade of phase transitions and Dirac revivals in magic-angle graphene. Nature 582, 203–208 (2020).
Kerelsky, A. et al. Maximized electron interactions at the magic angle in twisted bilayer graphene. Nature 572, 95–100 (2019).
Xie, Y. et al. Spectroscopic signatures of many-body correlations in magic-angle twisted bilayer graphene. Nature 572, 101–105 (2019).
Choi, Y. et al. Electronic correlations in twisted bilayer graphene near the magic angle. Nat. Phys. 15, 1174–1180 (2019).
Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059–1064 (2019).
Cao, Y. et al. Nematicity and competing orders in superconducting magic-angle graphene. Science 372, 264–271 (2021).
Saito, Y., Ge, J., Watanabe, K., Taniguchi, T. & Young, A. F. Independent superconductors and correlated insulators in twisted bilayer graphene. Nat. Phys. 16, 926–930 (2020).
Choi, Y. et al. Correlation-driven topological phases in magic-angle twisted bilayer graphene. Nature 589, 536–541 (2021).
Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).
Lin, J.-X. et al. Spin-orbit–driven ferromagnetism at half moiré filling in magic-angle twisted bilayer graphene. Science 375, 437–441 (2022).
Tseng, C.-C. et al. Anomalous hall effect at half filling in twisted bilayer graphene. Nat. Phys. 18, 1038–1042 (2022).
Serlin, M. et al. Intrinsic quantized anomalous hall effect in a moiré heterostructure. Science 367, 900–903 (2020).
Wu, S., Zhang, Z., Watanabe, K., Taniguchi, T. & Andrei, E. Y. Chern insulators, van Hove singularities and topological flat bands in magic-angle twisted bilayer graphene. Nat. Mater. 20, 488–494 (2021).
Cao, Y. et al. Strange metal in magic-angle graphene with near Planckian dissipation. Phys. Rev. Lett. 124, 076801 (2020).
Rozen, A. et al. Entropic evidence for a Pomeranchuk effect in magic-angle graphene. Nature 592, 214–219 (2021).
Saito, Y. et al. Isospin Pomeranchuk effect in twisted bilayer graphene. Nature 592, 220–224 (2021).
Paul, A. K. et al. Interaction-driven giant thermopower in magic-angle twisted bilayer graphene. Nat. Phys. https://doi.org/10.1038/s41567-022-01574-3 (2022).
Ramires, A. & Lado, J. L. Emulating heavy fermions in twisted trilayer graphene. Phys. Rev. Lett. 127, 026401 (2021).
Hu, H., Bernevig, B. A. & Tsvelik, A. M. Kondo lattice model of magic-angle twisted-bilayer graphene: Hund’s rule, local-moment fluctuations, and low-energy effective theory. Phys. Rev. Lett. 131, 026502 (2023).
Song, Z.-D. & Bernevig, B. A. Magic-angle twisted bilayer graphene as a topological heavy fermion problem. Phys. Rev. Lett. 129, 047601 (2022).
Shi, H. & Dai, X. Heavy-fermion representation for twisted bilayer graphene systems. Phys. Rev. B 106, 245129 (2022).
Cha, P., Patel, A. A. & Kim, E.-A. Strange metals from melting correlated insulators in twisted bilayer graphene. Phys. Rev. Lett. 127, 266601 (2021).
Merino, R. L. et al. Evidence of heavy fermion physics in the thermoelectric transport of magic angle twisted bilayer graphene. Preprint at https://arxiv.org/abs/2402.11749 (2024).
Batlle-Porro, S. et al. Cryo-near-field photovoltage microscopy of heavy-fermion twisted symmetric trilayer graphene. Preprint at https://arxiv.org/abs/2402.12296 (2024).
Călugăru, D. et al. The thermoelectric effect and its natural heavy fermion explanation in twisted bilayer and trilayer graphene. Preprint at https://arxiv.org/abs/2402.14057 (2024).
Li, Y., Fregoso, B. M. & Dzero, M. Topological mixed valence model in magic-angle twisted bilayer graphene. Phys. Rev. B 110, 045123 (2024).
Chou, Y.-Z. & Das Sarma, S. Kondo lattice model in magic-angle twisted bilayer graphene. Phys. Rev. Lett. 131, 026501 (2023).
Lau, L. L. & Coleman, P. Topological mixed valence model for twisted bilayer graphene. Preprint at https://arxiv.org/abs/2303.02670 (2023).
Mukerjee, S. Thermopower of the hubbard model: effects of multiple orbitals and magnetic fields in the atomic limit. Phys. Rev. B 72, 195109 (2005).
Chaikin, P. M. & Beni, G. Thermopower in the correlated hopping regime. Phys. Rev. B 13, 647–651 (1976).
Peterson, M. R. & Shastry, B. S. Kelvin formula for thermopower. Phys. Rev. B 82, 195105 (2010).
Zuev, Y. M., Chang, W. & Kim, P. Thermoelectric and magnetothermoelectric transport measurements of graphene. Phys. Rev. Lett. 102, 096807 (2009).
Checkelsky, J. G. & Ong, N. P. Thermopower and nernst effect in graphene in a magnetic field. Phys. Rev. B 80, 081413 (2009).
Nam, S.-G., Ki, D.-K. & Lee, H.-J. Thermoelectric transport of massive Dirac fermions in bilayer graphene. Phys. Rev. B 82, 245416 (2010).
Wang, C.-R. et al. Enhanced thermoelectric power in dual-gated bilayer graphene. Phys. Rev. Lett. 107, 186602 (2011).
Duan, J. et al. High thermoelectricpower factor in graphene/hBN devices. Proc. Natl Acad. Sci. USA 113, 14272–14276 (2016).
Ghahari, F. et al. Enhanced thermoelectric power in graphene: violation of the Mott relation by inelastic scattering. Phys. Rev. Lett. 116, 136802 (2016).
Mahapatra, P. S. et al. Misorientation-controlled cross-plane thermoelectricity in twisted bilayer graphene. Phys. Rev. Lett. 125, 226802 (2020).
Ghosh, A. et al. Evidence of compensated semimetal with electronic correlations at charge neutrality of twisted double bilayer graphene. Commun. Phys. 6, 360 (2023).
Cutler, M. & Mott, N. F. Observation of Anderson localization in an electron gas. Phys. Rev. 181, 1336–1340 (1969).
Silva, W. C. d. F. et al. Effects of strong electronic interactions on the thermopower properties of the repulsive Hubbard model. Phys. Rev. B 108, 075101 (2023).
Po, H. C., Zou, L., Vishwanath, A. & Senthil, T. Origin of Mott insulating behavior and superconductivity in twisted bilayer graphene. Phys. Rev. X 8, 031089 (2018).
Ledwith, P. J., Khalaf, E. & Vishwanath, A. Strong coupling theory of magic-angle graphene: a pedagogical introduction. Ann. Phys. 435, 168646 (2021).
Jonson, M. & Girvin, S. M. Thermoelectric effect in a weakly disordered inversion layer subject to a quantizing magnetic field. Phys. Rev. B 29, 1939–1946 (1984).
Yu, J. et al. Correlated hofstadter spectrum and flavour phase diagram in magic-angle twisted bilayer graphene. Nat. Phys. 18, 825–831 (2022).
Wei, P., Bao, W., Pu, Y., Lau, C. N. & Shi, J. Anomalous thermoelectric transport of Dirac particles in graphene. Phys. Rev. Lett. 102, 166808 (2009).
Acknowledgements
A.D. thanks D. K. Efetov, A. Bernevig and M. Jain for the useful discussions. We are grateful to A. Kumar Paul for initial help in measurements and U. Roy for numerous discussions on the fabrication of twisted heterostructures and measurements. A.D. thanks the Department of Science and Technology (DST) and Science and Engineering Research Board (SERB), India, for financial support SP/SERB-22-0387, DST/NM/TUE/QM-5/2019(C)/1 and IPA/2020/000034. A.D. also thanks CEFIPRA project SP/IFCP-22-0005. For growing the hBN crystals, we received support from the Japan Society for the Promotion of Science (KAKENHI grant nos. 19H05790, 20H00354 and 21H05233) to K.W. and T.T. N.T. thanks Indian Institute of Science, Bangalore, for their hospitality during her sabbatical. N.T. acknowledges partial support from NSF-DMS grant no. 2138905 and also acknowledges S. Dhawan for hosting at IISc and collaboration.
Author information
Authors and Affiliations
Contributions
A.G. contributed to developing measuring codes and carried out the measurements, data acquisition, and analysis. S.C. and R.D. contributed to the device fabrication, and S.C. also contributed to measurements. A.A. developed atomic orbital and cluster calculations. S.B. contributed to DMFT and HF calculations. A.A., S.B., S.M. and N.T. contributed to the development of the theory, and N.T. contributed to the understanding of data. K.W. and T.T. synthesized the hBN single crystals. A.D. contributed to conceiving the idea and designing the experiment, data interpretation, and analysis. All the authors contributed to the data interpretation and writing the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Yang-Zhi Chou and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Sections 1–16 and Figs. 1–30.
Source data
Source Data Fig. 1
Contains subfolders named Fig. 1c and Fig. 1d, which include .txt files of figure and .m MATLAB script file to get the plots as MATLAB figures.
Source Data Fig. 2
Contains subfolders named Fig. 2a, Fig. 2b, etc., which include .txt files of figure and .m MATLAB code file to get the plots as MATLAB figures.
Source Data Fig. 3
Contains subfolders named Fig. 3a, Fig. 3b, etc., which include .txt files of figure and .m MATLAB code file to get the plots as MATLAB figures.
Source Data Fig. 4
Contains subfolders named Fig. 4a, Fig. 4b, etc. which include .txt files of figure and .m MATLAB code file to get the plots as MATLAB figures.
Source Data Fig. 5
Contains subfolders named Fig. 5a, Fig. 5b, etc., which include .txt files of figure and .m MATLAB code file to get the plots as MATLAB figures.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Ghosh, A., Chakraborty, S., Dutta, R. et al. Thermopower probes of emergent local moments in magic-angle twisted bilayer graphene. Nat. Phys. 21, 732–739 (2025). https://doi.org/10.1038/s41567-025-02849-1
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41567-025-02849-1
This article is cited by
-
Thermopower reveals localized electrons
Nature Physics (2025)
-
Parallel-Conduction-Based Thermoelectric Responses in Chemical Vapor Deposition Grown Twisted Bilayer Graphene
Electronic Materials Letters (2025)