Main

Unlike ferromagnetism, spin order in antiferromagnets was not trivial from the very beginning, as the intuitive classical antiparallel spin order, or the Néel order, was known to be incompatible with the quantum antiferromagnetic Hamiltonian1. It was only after the first neutron diffraction study performed on MnO in 1949 that the classical Néel order was directly proven in simple two-sublattice antiferromagnets2,3. Since then, antiferromagnetism has always been at the heart of condensed-matter physics, as a wide variety of ordered and quantum disordered states, depending on lattice geometry, dimensionality and spin size, has been demonstrated, ranging from the non-collinear helical4,5 and skyrmionics6 order in the chiral or geometrically frustrated magnets, to the exactly solvable quantum spin liquid state in the honeycomb Kitaev system7. It is, however, emphasized here that all these intriguing antiferromagnetically ordered (disordered) states have been found in systems with lattice translational invariance, that is, periodic crystals.

Quasicrystals (QCs) are a new class of solids with crystallographically forbidden symmetries, such as 5-fold, 10-fold and 12-fold rotational symmetries. Since their discovery8, considerable attention has been focused on the possible formation of antiferromagnetic QCs from both theoretical9,10,11,12,13,14,15,16 and experimental17,18,19,20 points of view. On the theoretical side, antiferromagnetic orders in two-dimensional QCs such as decagonal11 and octagonal tilings9 were extensively investigated, whereas theoretical studies on three-dimensional icosahedral QCs (iQCs) are very scarce. Nonetheless, there is a symmetry-based argument16 that even the simple antiferromagnetic order, where half of the spins are up and the rest are down, is possible in a certain type of iQC, that is, primitive and body-centred iQCs. By contrast, on the experimental side, most magnetic iQCs exhibit spin-glass-like freezing behaviours as described below, and it is only recently that ferromagnetic orders have been discovered in Au–Ga–R (R = Gd, Tb, Dy) iQCs21,22.

The discovery of the ferromagnetic iQCs is of substantial importance primarily because they have opened a new research field in condensed-matter physics, also providing new perspectives towards QC spintronics. However, the observation of ferromagnetic iQCs might not be regarded as a big surprise since translational periodicity is not a necessary condition for ferromagnetic order establishment, that is, a ferromagnetic order can occur in any kind of material provided that the major magnetic interactions are ferromagnetic. In striking contrast, however, the existence of antiferromagnetic order in real QCs is by no means self-evident. As a matter of fact, so far, except for the above ferromagnetic iQCs21,22, all the reported rare-earth (R)-containing ternary iQCs such as Zn–Mg–R (refs. 23,24,25) and Cd–Mg–R (refs. 26,27,28,29,30) iQCs exhibit a spin-glass-like freezing behaviour without long-range magnetic order or reflections in the neutron diffraction data, which manifests the existence of frustration in real QCs. For example, binary Cd–R (ref. 31) iQCs, which have no chemical disorder on the non-magnetic sites, display spin-glass-like behaviours, whereas their periodic counterparts Cd–R approximant crystals commonly exhibit antiferromagnetic transitions. These observations have unwillingly led to a conjecture that antiferromagnetic order may be incompatible with quasiperiodicity31. For this reason, the discovery of an antiferromagnetic QC will certainly bring a big surprise to the condensed-matter physics community. Here it is worthwhile to note the difference between incommensurate and quasiperiodic magnetic structures. In incommensurate magnetic structures, the magnetic unit cell is periodic, but its period is incommensurate with the period of the underlying nuclear lattice, whereas in the quasiperiodic magnetic structures, the quasiperiodicity is intrinsic to the nuclear structure itself. Thus, there is no periodicity in either nuclear or magnetic structures in QCs.

Four decades after the discovery of QCs, here we report the first observation of an antiferromagnetic order in an iQC. As was the case for antiferromagnetism in a periodic crystalline material, first demonstrated in MnO in 1951 (ref. 3), this work presents the first neutron diffraction evidence of antiferromagnetism in a quasiperiodic material. This discovery decisively resolves the long-standing issue of whether antiferromagnetic orders are possible in real QCs, thereby opening a new research field of quasiperiodic antiferromagnets in condensed-matter physics.

Sample preparation and characterization

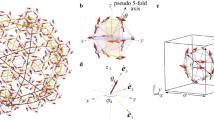
In our quest for new magnetic Au–semimetal–R iQCs motivated by the recent discoveries of ferromagnetic Au–Ga–R iQCs21,22, a novel iQC was identified in the Au–In–Eu system in the as-cast state. Figure 1a shows the powder X-ray diffraction (XRD) pattern of the Au56In28.5Eu15.5 alloy prepared using the conventional arc-melting solidification method. All the peaks can be indexed as a primitive iQC with quasilattice constant a6D = 7.89(1) Å, indicating the formation of a single-phase iQC. Figure 1b–d shows the electron diffraction patterns taken along the 5-fold, 3-fold and 2-fold axes, respectively, providing clear evidence of the intrinsic icosahedral symmetry of Au56In28.5Eu15.5. In Fig. 1b, a τ-scaling rule (τ is the golden mean) is observed for intense Bragg spots, further confirming the formation of a primitive iQC. Hence, the new Au–In–Eu iQC can be regarded as a Tsai-type iQC and is isostructural to the prototype Cd5.7Yb primitive iQC32.

Fig. 1: QC phase characterization.
figure 1

a, Powder XRD pattern of the Au56In28.5Eu15.5 iQC. b–d, Selected-area electron diffraction patterns taken along the 5-fold, 3-fold and 2-fold axes. The τ-scaling rule of intense Bragg spots in b indicates the formation of a primitive iQC. e, Spatial configuration of the R atoms in the structure of the iQC, viewed along a five-fold axis. A single icosahedron and acute rhombohedron units, composed of R elements on the vertices and along the long-body diagonal axis, respectively, are also shown. The R atoms belonging to each unit are shown in different colours for distinction.

Full size image

The structure of the Tsai-type iQC is schematically shown in Fig. 1e, where only the magnetic (R) atoms are displayed for clarity. The Tsai-type iQC is described as a quasiperiodic arrangement of a rhombic triacontahedron cluster composed of five concentric shells—from the centre, a tetrahedron, a dodecahedron, an icosahedron, an icosidodecahedron and a rhombic triacontahedron32. A characteristic feature of the rhombic triacontahedron cluster is that magnetic R atoms exclusively occupy the third icosahedral shell, whereas all the other shells are occupied by non-magnetic atoms. An additional building unit necessary for Tsai-type iQC is the so-called acute rhombohedron, which contains two R atoms at the long-body diagonal positions.

Magnetic properties of the Au56In28.5Eu15.5 iQC

Supplementary Fig. 1 shows the inverse magnetic susceptibility H/M of the Au56In28.5Eu15.5 iQC plotted as a function of temperature. The H/M–T data show excellent linearity across a wide temperature region between approximately 25 K and 300 K, well obeying the Curie–Weiss law \({{\chi }}={N}_{{\rm{A}}}{\mu }_{{\rm{eff}}}^{2}/3{k}_{{\rm{B}}}\left(T-{\varTheta }_{{\rm{p}}}\right)\), where NA, μeff, kB and Θp represent the Avogadro number, effective magnetic moment, Boltzmann constant and Weiss temperature, respectively. The fitting to the Curie–Weiss law between 50 K and 300 K yields μeff = 7.98μB and Θp = 3.41 K, with μeff being very close to the theoretical value of a free Eu2+ ion (7.94μB), which suggests that Eu is in a divalent state with zero orbital angular momentum (L = 0), sharing the same electron configuration (4f; ref. 7) as that of Gd3+. The positive Θp value manifests dominant ferromagnetic interactions in the Au56In28.5Eu15.5 iQC, in contrast to negative Θp values observed in previous spin-glass iQCs.

Figure 2a shows the magnetic susceptibility M/H of the Au56In28.5Eu15.5 iQC as a function of temperature below 20 K under zero-field-cooled (ZFC) and field-cooled (FC) conditions. A sharp cusp is clearly discernible at TN = 6.5 K in both ZFC and FC magnetization curves. Here no bifurcation between the ZFC and FC magnetizations is apparent below TN, suggesting the occurrence of an antiferromagnetic transition in the iQC, which is in sharp contrast to spin-glass iQCs, for which prominent hysteresis due to spin-glass-like freezing is evident below the freezing temperature Tf. Figure 2a (inset) shows the specific heat Cp of the Au56In28.5Eu15.5 iQC as a function of temperature below 20 K, together with its temperature derivative dCp/dT. A pronounced peak at TN = 6.5 K, as evidenced by the dCp/dT–T curve, further verifies that the observed magnetization cusp at TN = 6.5 K is due to a magnetic transition, that is, an antiferromagnetic transition. Furthermore, a.c. magnetic susceptibility measurements exhibit no frequency dependence of the peak at 6.5 K for the present Au56In28.5Eu15.5 iQC, unlike the corresponding Au–In–Eu 1/1 approximant crystal that enters a spin-glass state and showcases a clear frequency dependence of magnetic susceptibility (Supplementary Fig. 2).

Fig. 2: Bulk magnetization.
figure 2

a, Magnetic susceptibility (M/H) of the Au56In28.5Eu15.5 iQC as a function of temperature below 20 K under ZFC and FC conditions. The inset shows specific heat Cp of the same compound as a function of temperature together with its temperature derivative dCp/dT. b, Field-dependent magnetization of the Au56In28.5Eu15.5 iQC at T = 0.4 K, 1.8 K, 3 K, 4 K, 5 K, 6 K and 10 K up to 7 T. The inset shows the first derivative of the magnetization curves versus the magnetic field at various temperatures up to 1 T. The second derivative of dM/dH shows the position of metamagnetic anomalies taking place under 0.80 T, 0.67 T, 0.57 T and 0.42 T at 0.4 K, 1.8 K, 3 K and 4 K, respectively, which is a characteristic feature of antiferromagnetic transitions.

Full size image

Figure 2b presents the field-dependent magnetization of the Au56In28.5Eu15.5 iQC up to 7 T. The magnetization at the lowest temperature, that is, 0.4 K, reaches almost 7μB/Eu, that is, the full moment of a Eu2+ ion, showing full magnetic saturation to a forced ferromagnetic state at 7 T. Figure 2b (inset) shows the dM/dH–H curves obtained from the M–H data within fields up to 1 T, which commonly exhibit a maximum at a low magnetic field below TN, capturing the existence of a metamagnetic anomaly—another characteristic feature of antiferromagnetic transitions. We note that no other anomaly is observed at higher magnetic fields, showing only a gradual magnetic saturation towards 7μB/Eu, that is, a forced ferromagnetic state.

Neutron diffraction of the Au56In28.5Eu15.5 iQC

Neutron powder diffraction patterns measured at T = 10 K (above TN = 6.5 K) and T = 3 K (below TN) are shown in Fig. 3a. At 10 K, most of the peaks are well indexed using the six-dimensional (6D) indices with the Penrose edge length a = 5.5351(4) Å (a6D = a × \(\sqrt{2}\) = 7.828 Å), being in perfect agreement with a6D = 7.89(1) Å obtained from the powder XRD pattern shown in Fig. 1a. This confirms the QC nature of the present Au–In–Eu sample. There are a few unindexed peaks, which are attributed to powder diffraction peaks of either vanadium (sample can material) or aluminium (cryostat material) and, hence, are extrinsic. Here we note that no trace of impurity phase was detected (within the resolution limits) in the specimen used for the neutron diffraction experiments, as shown in the scanning electron microscopy images (Supplementary Fig. 3) and powder XRD pattern (Fig. 1a). We also confirmed that the unindexed peaks do not change in intensity across the transition temperature and, thus, they are not magnetic peaks.

Fig. 3: Neutron powder diffraction.
figure 3

a, Neutron powder diffraction patterns measured at T = 10 K (above TN = 6.5 K; blue) and T = 3 K (below TN; violet) in the Au56In28.5Eu15.5 iQC. The vertical solid lines at the bottom stand for the positions of the nuclear Bragg reflections expected for the icosahedral phase with the 6D indices (|Q⊥| < 0.74 Å−1). The lattice constant a (edge length of the 3D Penrose lattice) was 5.5351(4) Å at T = 10 K. The violet arrows indicate the positions at which the additional magnetic Bragg peaks appear at T = 3 K. The yellow arrows indicate peaks that cannot be indexed by the 6D indices. Most of them are attributed to the Bragg peaks of either aluminium or vanadium, which are used for the sample can or the cryostat wells. b, Temperature difference I(T = 3 K) – I(T = 10 K) in the low 2θ < 60° range. Three peaks (indicated by the arrows) were detected. The blue vertical solid lines at the bottom denote the positions of the integer 6D indices (|Q⊥| < 0.74 Å−1), whereas the violet solid lines represent the 6D indices with a doubled (magnetic) unit cell (|Q⊥| < 0.36 Å−1), both with a = 5.5351 Å. c, Temperature dependence of the magnetic Bragg reflection appeared at 2θ = 32.8° (Q = 2.16 Å−1) in a obtained using the triple-axis spectrometer ISSP-GPTAS located at JRR-3, Japan. The data were collected in a heating run. The abrupt increase in the reflection intensity was clearly seen at TN = 6.3 K, consistent with TN = 6.5 K obtained in the bulk experiment. The Ei stands for the incident neutron energy. The error bars correspond to one standard deviation assuming Poisson distribution for neutron counts. For the temperature difference, proper error propagation was taken into account.

Full size image

At T = 3 K, we found the appearance of magnetic Bragg peaks at 2θ ≈ 12°, 26.5° and 32°. They are clearly visible by taking the temperature difference (Fig. 3b). Temperature dependence of the magnetic Bragg intensity was collected for all the newly appeared peaks. They consistently show an abrupt increase at TN = 6.5 K. A representative result for the highest 2θ (at ~32°; Fig. 3a) is shown in Fig. 3c. Temperature dependence of other magnetic reflections, as well as powder diffraction patterns in a narrower 2θ range, is shown in Supplementary Figs. 4 and 5. The transition temperature obtained from the neutron diffraction experiment (TN = 6.3 K) is in excellent agreement with that observed in the bulk magnetic measurement (TN = 6.5 K). This confirms that the Bragg peaks appearing below TN are evidently attributed to the magnetic long-range order in the QC phase.

To confirm the antiferromagnetic nature of the newly appearing peaks and to identify their possible indices, we performed combined Rietveld and Pawley fitting with the 6D indices considering a doubled magnetic unit cell (2a6D × 2a6D × 2a6D × 2a6D × 2a6D × 2a6D), where 2a6D (aM6D) = 15.656 Å. The details of the fitting procedure are described in the Supplementary Information, and the fitting results are shown in Fig. 3b and Supplementary Fig. 6a–c. Clearly, all three peaks are well reproduced in the fitting using the 6D indices, with each peak consisting of two reflections. The fact that the magnetic peak profile is well reproduced by the present Pawley fitting with profile function parameters using the standard values indicates that the intrinsic widths of the magnetic reflections are resolution limited, suggesting the long-range nature of the antiferromagnetic ordering. Note that the reflections contributing to the magnetic peaks (Fig. 3b, arrows) have at least one odd number in their reflection indices. Indeed, it was shown that all-even indices cannot reproduce the appearance of the magnetic reflection (Supplementary Fig. 6). Hence, we conclude that the observed magnetic reflections clearly indicate an antiferromagnetic order with a doubled unit cell. This is in striking contrast to the case of the ferromagnetic iQC23, where the magnetic reflections were explained using integer 6D indices of the chemical unit cell.

It should be noted, however, that for the indices suggested from the Pawley fitting, that is, 1011111M, 101200M, 322111M, \({20\bar{2}023}_{{\rm{M}}}\), \({1330\bar{3}\bar{1}}_{{\rm{M}}}\) and \({133\bar{1}\bar{3}\bar{1}}_{{\rm{M}}}\) (the suffix ‘M’ is for indices for the doubled magnetic unit cell), we were unable to find a single magnetic q vector solution. Due to the small number of observed magnetic Bragg peaks (partly because of the strong absorption of the present sample) and high density of candidate reflections (due to quasiperiodicity), we are reluctant to draw conclusions about the details of the antiferromagnetic order; whether the antiferromagnetic order is of multi-q type or a single q vector could explain all the reflections. We would leave this interesting issue, that is, the determination of the magnetic modulation and structure in the antiferromagnetic QC, for future study.

Discussion and outlook

The present work provides the first experimental evidence of antiferromagnetic order in a real QC. As previously mentioned, no observations of an antiferromagnetic iQC have been reported in the literature for more than four decades since the discovery of QCs. The discovery of an antiferromagnetic phase in the Au–In–Eu system has now posed a new question as to why it exhibits an antiferromagnetic order. Here we address one notable feature of the present Au–In–Eu iQC, which is markedly different from previous R-containing magnetic iQCs. Unlike the previous iQCs that commonly show negative Θp values, the Au–In–Eu iQC exhibits a positive Θp value. Meanwhile, a systematic study on magnetic approximant crystals33 has shown that both ferromagnetic and antiferromagnetic orders are stabilized only in the positive-Θp region, whereas the spin-glass phase prevails predominantly in the negative-Θp region, indicating the existence of strong geometrical frustration in the negative-Θp region. Thus, the present antiferromagnetic order with positive Θp is indeed consistent with the trend observed in approximant crystals33. As demonstrated later, a slight decrease in the Θp value in the Au–In–Eu iQC leads to a phase transformation from the antiferromagnetic phase into a spin-glass state, clearly showing that a further increase in antiferromagnetic interactions does cause magnetic frustration.

Next, we discuss the variation in magnetic order with increasing electron-per-atom (e/a) ratio through the partial substitution of tetravalent Sn into the monovalent Au and trivalent In sites. A single-phase iQC was found to form up to the addition of 3 at.% Sn, as presented in Supplementary Fig. 7, which shows the superposed powder XRD patterns of the Au54In27.5Sn3Eu15.5 sample and antiferromagnetic Au56In28.5Eu15.5 iQC. This tetravalent element substitution increases the e/a ratio from 1.73 to 1.80. The detailed results of the magnetic measurements on the Au–In–Sn–Eu iQC are summarized in the Supplementary Information. As shown in Supplementary Fig. 8, the Curie–Weiss fitting yields μeff = 7.95μB and Θp = 1.88 K in the Au–In–Sn–Eu iQC; thus, Θp decreases from 3.41 K to 1.88 K, indicating a relative enhancement in antiferromagnetic contributions.

Importantly, the temperature-dependent magnetization of the Au–In–Sn–Eu iQC now exhibits a clear bifurcation between the ZFC and FC magnetizations below the cusp temperature of Tf = 4.1 K (Supplementary Fig. 9). Moreover, as shown in Supplementary Fig. 10, the metamagnetic anomaly in the field-dependent magnetization present in the Au–In–Eu iQC disappears with an increase in the e/a ratio, both of which are characteristic features commonly observed in previous spin-glass iQCs. Thus, a slight increase in the e/a ratio or a slight enhancement in antiferromagnetic contributions destabilizes the antiferromagnetic order, showing that a spin-glass region exists next to the antiferromagnetic region in the e/a parameter space, and further reduction in Θp gives rise to magnetic frustration. Therefore, we have now come to the conclusion that the absence of antiferromagnetic orders in previous iQCs is due to this magnetic frustration induced by the presence of considerable antiferromagnetic contributions: note that all the previous spin-glass iQCs are situated in the negative-Θp region. This discovery will undoubtedly trigger a revival of extensive exploration of antiferromagnetic orders in iQCs that have remained unexplored until now, especially in the positive-Θp region, by controlling the e/a ratio through composition tuning and/or heterovalent element substitution, as demonstrated in this work.

One central as well as fundamental issue in condensed-matter physics has been to identify a quasiperiodic order parameter beyond the atomic position (or the electron density) that was first discovered by Shechtman8. In this respect, the present quasiperiodic antiferromagnetic order represents the first non-trivial quasiperiodic order parameter, beyond atomic QCs, and may be regarded as the second type of quasiperiodicity found in nature. It is intriguing that the present antiferromagnetic order was found in a magnetic QC having a primitive icosahedral lattice, in which the simple antiferromagnetic order is shown to be possible16. We would, however, emphasize here that the magnetic structure is yet to be solved; it may be the simple antiferromagnetic or much more complex non-collinear and/or non-coplanar type, as suggested from the magnetic structures in related approximants. This very intriguing subject is left for future study.

The present discovery will stimulate both experimental and theoretical efforts to elucidate not only its unique magnetic structure but also the intrinsic properties of the quasiperiodic order parameter. More broadly, our findings will contribute to the understanding of magnetism in quasiperiodic systems, where the wavevector is not a good quantum number for describing electrons, phonons, magnons and so on.

Another exciting aspect of magnetically ordered QCs is their potential for new applications such as functional materials in spintronics. For instance, ferromagnetically ordered iQCs can potentially exhibit near-zero magnetocrystalline anisotropy due to their inherent high symmetry, that is, m35 or 235. Equally interesting magnetic properties reflecting the unprecedented high symmetry, such as ultrasoft magnetic response, may be expected in antiferromagnetic QCs.

Finally, it would be interesting to mention that various topologically non-trivial magnetic textures inherent to the unique geometry of the common R icosahedron have been extensively investigated recently, where the topological charge34 n = Ω/(4π)is defined in terms of the solid angle Ω spanned by the 12 localized spins on the R icosahedron. A unique whirling antiferromagnetic order with an unusually large topological charge of n = 3 was discovered experimentally in Au–SM (SM = Al, Ga)–Tb 1/1 approximant crystals18,35,36, and a unique hedgehog order with a topological charge of n = 1 was theoretically predicted in Au–Ga–R iQCs34,37,38. Thus, the present discovery has opened a new route not only to unprecedented quasiperiodic antiferromagnetic orders but also to quasiperiodic topological magnetic orders, realized in quasiperiodic antiferromagnets.

Methods

Synthesis

Ternary Au56In28.5Eu15.5 and Au54In27.5Sn3Eu15.5 iQC alloys were synthesized using the arc-melting technique. High-purity raw elements of Au (99.99 wt%), In (99.99 wt%) and Eu (99.9 wt%) were utilized in the synthesis process. During the arc-melting process, a relatively low current of 70 A is applied to melt the raw materials and to prevent the vapourization of Eu. The samples are flipped and remelted three times to ensure compositional homogenization. At the final stage of melting, to prevent the precipitation of second phases during cooling, the melt is rapidly cooled by immediately reducing the current from 70 A to 0 A.

Characterization

Phase identification was performed through powder XRD analysis using a Rigaku SmartLab SE X-ray diffractometer with Cu Kα radiation. To index the powder XRD pattern and estimate the 6D lattice parameter (a6D), Elser’s method was used. The reported a6D value in this study is an average of the estimates derived from the 211111, 221001 and 332002 peaks.

For phase characterization, selected-area electron diffraction patterns were acquired using the JEM-2010F transmission electron microscope located at the Advanced Research Infrastructure for Materials and Nanotechnology, the University of Tokyo. To prepare the sample for selected-area electron diffraction analysis, the bulk material was initially crushed in ethanol, and the resulting small particles were then transferred onto a copper grid.

For microstructural characterization, scanning electron microscopy (JEOL JSM-IT100) was utilized.

Magnetization measurements

Bulk magnetization measurements were performed using a superconducting quantum interference device magnetometer, Quantum Design MPMS3. These measurements were carried out over a temperature range spanning from 0.4 K to 300 K, with an external d.c. field up to 7 × 104 Oe. Both ZFC and FC conditions were examined during these measurements.

Neutron diffraction

Neutron powder diffraction experiments were performed using the high-resolution powder diffractometer ECHIDNA installed at the OPAL reactor, Australian Nuclear Science and Technology Organization. Because of the high neutron absorption of all the constituent elements, namely, Au, In and Eu, neutrons with a relatively short wavelength (λ = 1.6220 Å) were selected using Ge 335 reflections. In addition, the powder sample was loaded in the double-walled vanadium can with inner and outer radii of 4.74 mm and 5.29 mm, respectively, to reduce the attenuation effect. The can was set in a closed-cycle 4He refrigerator with a base temperature of 3 K. A complementary neutron diffraction experiment was performed using the thermal-neutron triple-axis spectrometer ISSP-GPTAS installed at JRR-3. Incident neutrons with ki = 3.83 Å−1 (λ = 1.64 Å) were selected using pyrolytic graphite 002 reflections, and higher-order harmonic neutrons were removed using two pyrolytic graphite filters. To reduce the background, a triple-axis setup with a pyrolytic graphite 002 analyser was used, and 40′-40′-40′-80′ collimations were used. The finely pulverized sample was pasted on a single-crystal Si plate using CYTOP as a glue. The thickness of the Si plate was 0.5 mm, whereas the dimensions of the pasted pulverized sample were 38 mm (w) × 38 mm (h) × 0.4 mm (t). The sample-pasted plate was sealed in the Al sample can with the 4He exchange gas to achieve thermal homogeneity. The sample can was set to the closed-cycle 4He refrigerator with the Si plate bisecting the angle between –ki and kf, that is, the transmission geometry. The base temperature of the triple-axis experiment is approximately 3 K.

Neutron powder diffraction analysis

The neutron powder diffraction patterns of Au56In28.5Eu15.5 iQC were analysed using the custom-built Rietveld and Pawley analysis code msas6D, which is capable of refining the atomic structure of the QC using 6D crystallography (T.J.S., manuscript in preparation). The peak profile function used in the following analysis is the split pseudo-Voigt function39, and the profile parameters estimated using a standard alloy sample were used as the fixed parameters.

For the atomic structure analysis, the published crystal structure of Cd–Yb iQC32 was further simplified as follows. The shapes of the occupation domains (ODs) for all the atoms are approximated to be spherical (or spherical shell) instead of polyhedral40. The positions of the ODs in the 6D chemical unit cell are (0, 0, 0, 0, 0, 0) (V site), (1/2, 0, 0, 0, 0, 0) (E site), (1/2, 1/2, 1/2, 1/2, 1/2, 1/2) (B site) and (0, 1/4, 1/4, 1/4, 1/4, 1/4) (rare-earth site). Note that the rare-earth OD is not centred at the B site as assumed in the earlier refinement using the polyhedral ODs. This is because the polyhedral ODs at the B site assumed in the earlier refinement consist of several small ODs corresponding to different atoms. Indeed, the small ODs for the rare-earth atoms may be approximated by spherical ODs centred at (0, 1/4, 1/4, 1/4, 1/4, 1/4). For the analysis of the Au–In–Eu iQC, the rare-earth site is assumed to be fully occupied by Eu atoms, whereas other ODs are assumed to be randomly occupied by Au and In atoms with the ratio 56:28.5. Since the purpose of atomic structure refinement is just to obtain a reasonable nuclear reflection pattern that can be used to discriminate magnetic reflections and not to obtain the final atomic structure, we refine the outer radii of the ODs only with fixed occupancy (the OD of the B site is a spherical shell with the inner radius fixed to 7.95 Å, whereas all the other ODs are spherical). The resulting radii of the ODs are 6.2(2) Å, 6.58(6) Å, 8.4(1) Å and 4.00(4) Å for the V, E, B and rare-earth sites, respectively. Nonetheless, we do not claim that these values represent the correct 6D atomic structure due to the oversimplifications in the present modelling. The lattice parameter (Penrose edge length) a is refined as 5.5351(4) Å at T = 10 K, which gives the 6D lattice constant a6D = 7.8277 Å.

The magnetic reflections were fitted assuming that the magnetic unit cell in six dimensions is doubled compared with the chemical unit cell. Accordingly, the lattice parameter for the 6D magnetic unit cell is fixed to 2a6D = 15.656 Å (that is, the magnetic unit cell size 2a6D × 2a6D × 2a6D × 2a6D × 2a6D × 2a6D) in the magnetic peak refinement. Due to the lack of any magnetic structure model in the 6D space at present, we use the Pawley method41 to fit the magnetic diffraction pattern with all the integer indices with the perpendicular space component |Q⊥| < 0.36 Å−1. Only the reflections up to 2θ = 40° are included in the magnetic fitting, as the magnetic intensity decreases rapidly at high 2θ.

The result of the combined Rietveld (nuclear) and Pawley (magnetic) fittings is shown in Supplementary Fig. 6a. Nuclear reflections appearing at around 2θ ≈ 35° are well fitted, indicating that the peak widths are resolution limited with the present instrumental resolution. The magnetic peaks (indicated by the arrows) are also well reproduced by the fitting. To observe the magnetic scattering part much closely, we performed Pawley fitting to the temperature-subtracted magnetic diffraction pattern. Figure 3b shows the result of the magnetic Pawley fitting with the doubled magnetic unit cell and |Q⊥| < 0.36 Å−1. Magnetic reflections are well indexed with indices that include at least one odd number, clearly confirming the antiferromagnetic nature of the magnetic reflections. Note that each magnetic peak is not from a single reflection, but possibly results from the overlap of two reflections, making it difficult to uniquely determine the magnetic modulation vector.

To further confirm the antiferromagnetic nature of the observed magnetic peaks, we performed the following two analyses. First, the temperature-subtracted magnetic diffraction pattern is Pawley fitted using larger |Q⊥| < 0.74 Å−1. It should be noted that this |Q⊥| range includes all nuclear reflections, such as 111000 (222000 in a doubled magnetic unit cell), as candidate magnetic reflections. The result of the fitting is shown in Supplementary Fig. 6b, which clearly indicates that all-even indices do not give substantial intensity contribution to the observed magnetic diffraction pattern, confirming the antiferromagnetic nature. Second, the T = 3 K diffraction pattern was fitted with the combined Rietveld and Pawley method, assuming integer indices of the original chemical unit cell for the magnetic reflections, the result of which is shown in Supplementary Fig. 6c. Clearly, the integer indices of the original chemical unit cell cannot reproduce the magnetic peak positions, conclusively excluding the ferromagnetic nature in this Au–In–Eu iQC.