Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Feedback between F-actin organization and active stress governs criticality and energy localization in the cell cytoskeleton

Nature Physics volume 21, pages 1290–1302 (2025)Cite this article

Subjects

Abstract

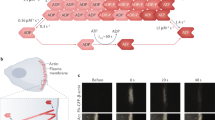
Self-organized criticality can occur in earthquakes, avalanches and biological processes, and is characterized by intermittent, scale-free energy dissipation. In living cells, the actin cytoskeleton undergoes dynamic structural reorganization, particularly during migration and division, where molecular motors generate mechanical stresses that drive large dissipative events. However, the mechanisms governing these critical transitions remain unclear. Here we show that cytoskeletal criticality emerges from the interplay between F-actin organization and active stress generation. Our study focuses on a minimal actomyosin system in vitro, which is composed of F-actin filaments, myosin II motors and nucleation-promoting factors. By systematically varying the actin connectivity and nematic order, we demonstrate that ordered and sparsely connected networks exhibit exponential stress dissipation, whereas disordered and highly connected networks show heavy-tailed distributions of energy release and the 1/f noise characteristic of self-organized criticality. Increased disorder leads to stress localization, shifting force propagation into stiffer mechanical modes, reminiscent of Anderson localization in condensed-matter systems. Furthermore, we show that network architecture directly regulates the myosin II filament size, establishing a chemical–mechanical feedback loop that modulates criticality. Our findings provide insights into the collective cytoskeletal dynamics, energy localization and cellular self-organization.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Actomyosin dynamics exhibit temporal criticality.
Fig. 2: F-actin architecture governs critical behaviour under myosin activity.
Fig. 3: Myosin motion follows a Lévy α distribution independent of the F-actin architecture.
Fig. 4: Criticality is determined by feedback between the F-actin architecture and myosin thick filament size.
Fig. 5: Branched F-actin networks dissipate energy through localized stiff modes.

Similar content being viewed by others

Data availability

Source data are provided with this paper. Raw data supporting the findings of this paper are available from the corresponding author upon reasonable request.

Code availability

Codes supporting the findings of this paper are available from the corresponding author upon reasonable request.

References

  1. Bak, P. & Tang, C. Earthquakes as a self‐organized critical phenomenon. J. Geophys. Res.: Solid Earth 94, 15635–15637 (1989).

    Article  Google Scholar 

  2. Wijngaarden, R. J., Welling, M. S., Aegerter, C. M. & Menghini, M. Avalanches and self-organized criticality in superconductors. Eur. Phys. J. B 50, 117–122 (2006).

    Article  ADS  Google Scholar 

  3. Negoro, H., Kitamoto, S., Takeuchi, M. & Mineshige, S. Statistics of X-ray fluctuations from Cygnus X-1: reservoirs in the disk? Astrophys. J. 452, L49 (1995).

    Article  ADS  Google Scholar 

  4. Bedard, C., Kroeger, H. & Destexhe, A. Does the 1/f frequency scaling of brain signals reflect self-organized critical states? Phys. Rev. Lett. 97, 118102 (2006).

    Article  ADS  Google Scholar 

  5. Chialvo, D. R. Emergent complex neural dynamics. Nat. Phys. 6, 744–750 (2010).

    Article  Google Scholar 

  6. Sneppen, K., Bak, P., Flyvbjerg, H. & Jensen, M. H. Evolution as a self-organized critical phenomenon. Proc. Natl Acad. Sci. USA 92, 5209–5213 (1995).

    Article  ADS  Google Scholar 

  7. Utsu, T. A statistical study on the occurrence of aftershocks. Geophys. Mag. 30, 521–605 (1961).

    Google Scholar 

  8. Ōmori, F. On the After-Shocks of Earthquakes (The Univ. of Tokyo, 1895).

  9. Bak, P., Christensen, K., Danon, L. & Scanlon, T. Unified scaling law for earthquakes. Phys. Rev. Lett. 88, 178501 (2002).

    Article  ADS  Google Scholar 

  10. Gutenberg, B. & Richter, C. F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 34, 185–188 (1944).

    Article  Google Scholar 

  11. Bak, P. & Chen, K. Self-organized criticality. Sci. Am. 264, 46–53 (1991).

    Article  ADS  Google Scholar 

  12. Bak, P. & Paczuski, M. The dynamics of fractals. Fractals 3, 415–429 (1995).

    Article  MathSciNet  Google Scholar 

  13. Bak, P., Tang, C. & Wiesenfeld, K. Self-organized criticality: an explanation of the 1/f noise. Phys. Rev. Lett. 59, 381 (1987).

    Article  ADS  Google Scholar 

  14. Bak, P. & Creutz, M. in Fractals in Science 27–48 (Springer, 1994).

  15. Davidsen, J. & Paczuski, M. 1/fα noise from correlations between avalanches in self-organized criticality. Phys. Rev. E 66, 050101 (2002).

    Article  ADS  Google Scholar 

  16. Beggs, J. M. & Plenz, D. Neuronal avalanches in neocortical circuits. J. Neurosci. 23, 11167–11177 (2003).

    Article  Google Scholar 

  17. Kobayashi, M. & Musha, T. 1/f fluctuation of heartbeat period. IEEE Trans. Biomed. Eng. 456–457 (1982).

  18. Akselrod, S. et al. Power spectrum analysis of heart rate fluctuation: a quantitative probe of beat-to-beat cardiovascular control. Science 213, 220–222 (1981).

    Article  ADS  Google Scholar 

  19. Hooge, F. & Hoppenbrouwers, A. Amplitude distribution of 1/f noise. Physica 42, 331–339 (1969).

    Article  ADS  Google Scholar 

  20. Voss, R. F. & Clarke, J. Flicker (1f) noise: equilibrium temperature and resistance fluctuations. Phys. Rev. B 13, 556 (1976).

    Article  ADS  Google Scholar 

  21. Alencar, A. M. et al. Non-equilibrium cytoquake dynamics in cytoskeletal remodeling and stabilization. Soft Matter 12, 8506–8511 (2016).

    Article  ADS  Google Scholar 

  22. Shi, Y., Porter, C. L., Crocker, J. C. & Reich, D. H. Dissecting fat-tailed fluctuations in the cytoskeleton with active micropost arrays. Proc. Natl Acad. Sci. USA 116, 13839–13846 (2019).

    Article  ADS  Google Scholar 

  23. Shi, Y. et al. Pervasive cytoquakes in the actomyosin cortex across cell types and substrate stiffness. Integr. Biol. 13, 246–257 (2021).

    Article  Google Scholar 

  24. Shi, Y., Sivarajan, S., Crocker, J. C. & Reich, D. H. Measuring cytoskeletal mechanical fluctuations and rheology with active micropost arrays. Curr. Protoc. 2, e433 (2022).

    Article  Google Scholar 

  25. Sivarajan, S. et al. Lévy-distributed fluctuations in the living cell cortex. Phys. Rev. Res. 6, 043265 (2024).

    Article  Google Scholar 

  26. Pollard, T. D. Mechanics of cytokinesis in eukaryotes. Curr. Opin. Cell Biol. 22, 50–56 (2010).

    Article  Google Scholar 

  27. Blanchoin, L., Boujemaa-Paterski, R., Sykes, C. & Plastino, J. Actin dynamics, architecture, and mechanics in cell motility. Physiol. Rev. 94, 235–263 (2014).

    Article  Google Scholar 

  28. Murrell, M., Oakes, P. W., Lenz, M. & Gardel, M. L. Forcing cells into shape: the mechanics of actomyosin contractility. Nat. Rev. Mol. Cell Biol. 16, 486–498 (2015).

    Article  Google Scholar 

  29. Smith, D. et al. Molecular motor-induced instabilities and cross linkers determine biopolymer organization. Biophys. J. 93, 4445–4452 (2007).

    Article  ADS  Google Scholar 

  30. Murrell, M. P. & Gardel, M. L. F-actin buckling coordinates contractility and severing in a biomimetic actomyosin cortex. Proc. Natl Acad. Sci. USA 109, 20820–20825 (2012).

    Article  ADS  Google Scholar 

  31. Silva, M. S. et al. Active multistage coarsening of actin networks driven by myosin motors. Proc. Natl Acad. Sci. USA 108, 9408–9413 (2011).

    Article  ADS  Google Scholar 

  32. Vogel, S. K., Petrasek, Z., Heinemann, F. & Schwille, P. Myosin motors fragment and compact membrane-bound actin filaments. eLife 2, e00116 (2013).

    Article  Google Scholar 

  33. Haviv, L., Gillo, D., Backouche, F. & Bernheim-Groswasser, A. A cytoskeletal demolition worker: myosin II acts as an actin depolymerization agent. J. Mol. Biol. 375, 325–330 (2008).

    Article  Google Scholar 

  34. Li, F. & Higgs, H. N. The mouse formin mDia1 is a potent actin nucleation factor regulated by autoinhibition. Curr. Biol. 13, 1335–1340 (2003).

    Article  Google Scholar 

  35. Cory, G. O., Cramer, R., Blanchoin, L. & Ridley, A. J. Phosphorylation of the WASP-VCA domain increases its affinity for the Arp2/3 complex and enhances actin polymerization by WASP. Mol. cell 11, 1229–1239 (2003).

    Article  Google Scholar 

  36. Cao, L. et al. SPIN90 associates with mDia1 and the Arp2/3 complex to regulate cortical actin organization. Nat. Cell Biol. 22, 803–814 (2020).

    Article  Google Scholar 

  37. Bovellan, M. et al. Cellular control of cortical actin nucleation. Curr. Biol. 24, 1628–1635 (2014).

    Article  Google Scholar 

  38. Carvalho, K. et al. Actin polymerization or myosin contraction: two ways to build up cortical tension for symmetry breaking. Philos. Trans. R. Soc. B 368, 20130005 (2013).

    Article  Google Scholar 

  39. Ideses, Y., Bernheim, A., Sonn, A. & Roichman, Y. Myosin II does it all: assembly, remodeling, and disassembly of actin networks are governed by myosin II activity. Biophys. J. 106, 568a–568a (2014).

    Article  ADS  Google Scholar 

  40. Lau, A. W., Hoffman, B. D., Davies, A., Crocker, J. C. & Lubensky, T. C. Microrheology, stress fluctuations, and active behavior of living cells. Phys. Rev. Lett. 91, 198101 (2003).

    Article  ADS  Google Scholar 

  41. Mizuno, D., Tardin, C., Schmidt, C. F. & Mackintosh, F. C. Nonequilibrium mechanics of active cytoskeletal networks. Science 315, 370–373 (2007).

    Article  ADS  Google Scholar 

  42. Toyota, T., Head, D. A., Schmidt, C. F. & Mizuno, D. Non-Gaussian athermal fluctuations in active gels. Soft Matter 7, 3234–3239 (2011).

    Article  ADS  Google Scholar 

  43. Ennomani, H. et al. Architecture and connectivity govern actin network contractility. Curr. Biol. 26, 616–626 (2016).

    Article  Google Scholar 

  44. Liman, J. et al. The role of the Arp2/3 complex in shaping the dynamics and structures of branched actomyosin networks. Proc. Natl Acad. Sci. USA 117, 10825–10831 (2020).

    Article  ADS  Google Scholar 

  45. Floyd, C., Levine, H., Jarzynski, C. & Papoian, G. A. Understanding cytoskeletal avalanches using mechanical stability analysis. Proc. Natl Acad. Sci. USA 118, e2110239118 (2021).

    Article  Google Scholar 

  46. Li, C., Liman, J., Eliaz, Y. & Cheung, M. S. Forecasting avalanches in branched actomyosin networks with network science and machine learning. J. Phys. Chem. B 125, 11591–11605 (2021).

    Article  Google Scholar 

  47. Floyd, C., Papoian, G. A. & Jarzynski, C. Quantifying dissipation in actomyosin networks. Interface Focus 9, 20180078 (2019).

    Article  Google Scholar 

  48. Swartz, D. W. & Camley, B. A. Active gels, heavy tails, and the cytoskeleton. Soft Matter 17, 9876–9892 (2021).

    Article  ADS  Google Scholar 

  49. Bernheim-Groswasser, A., Wiesner, S., Golsteyn, R. M., Carlier, M.-F. & Sykes, C. The dynamics of actin-based motility depend on surface parameters. Nature 417, 308–311 (2002).

    Article  ADS  Google Scholar 

  50. Backouche, F., Haviv, L., Groswasser, D. & Bernheim-Groswasser, A. Active gels: dynamics of patterning and self-organization. Phys. Biol. 3, 264 (2006).

    Article  ADS  Google Scholar 

  51. Bausch, A. & Kroy, K. A bottom-up approach to cell mechanics. Nat. Phys. 2, 231–238 (2006).

    Article  Google Scholar 

  52. Claessens, M. M., Bathe, M., Frey, E. & Bausch, A. R. Actin-binding proteins sensitively mediate F-actin bundle stiffness. Nat. Mater. 5, 748–753 (2006).

    Article  ADS  Google Scholar 

  53. Koenderink, G. H. et al. An active biopolymer network controlled by molecular motors. Proc. Natl Acad. Sci. USA 106, 15192–15197 (2009).

    Article  ADS  Google Scholar 

  54. Bendix, P. M. et al. A quantitative analysis of contractility in active cytoskeletal protein networks. Biophys. J. 94, 3126–3136 (2008).

    Article  ADS  Google Scholar 

  55. Lee, G. et al. Myosin-driven actin-microtubule networks exhibit self-organized contractile dynamics. Sci. Adv. 7, eabe4334 (2021).

    Article  ADS  Google Scholar 

  56. Ricketts, S. N., Ross, J. L. & Robertson-Anderson, R. M. Co-entangled actin-microtubule composites exhibit tunable stiffness and power-law stress relaxation. Biophys. J. 115, 1055–1067 (2018).

    Article  ADS  Google Scholar 

  57. Köster, D. V. et al. Actomyosin dynamics drive local membrane component organization in an in vitro active composite layer. Proc. Natl Acad. Sci. USA 113, E1645–E1654 (2016).

    Article  Google Scholar 

  58. Murrell, M., Thoresen, T. & Gardel, M. Chapter Fifteen—reconstitution of contractile actomyosin arrays. Methods Enzymol. 540, 265–282 (2014).

    Article  Google Scholar 

  59. Muresan, C. G. et al. F-actin architecture determines constraints on myosin thick filament motion. Nat. Commun. 13, 7008 (2022).

    Article  ADS  Google Scholar 

  60. Linsmeier, I. et al. Disordered actomyosin networks are sufficient to produce cooperative and telescopic contractility. Nat. Commun. 7, 12615 (2016).

    Article  ADS  Google Scholar 

  61. Stricker, J., Falzone, T. & Gardel, M. L. Mechanics of the F-actin cytoskeleton. J. Biomech. 43, 9–14 (2010).

    Article  Google Scholar 

  62. Thoresen, T., Lenz, M. & Gardel, M. L. Reconstitution of contractile actomyosin bundles. Biophys. J. 100, 2698–2705 (2011).

    Article  ADS  Google Scholar 

  63. Weirich, K. L. et al. Liquid behavior of cross-linked actin bundles. Proc. Natl Acad. Sci. USA 114, 2131–2136 (2017).

    Article  ADS  Google Scholar 

  64. Stam, S. et al. Filament rigidity and connectivity tune the deformation modes of active biopolymer networks. Proc. Natl Acad. Sci. USA 114, E10037–E10045 (2017).

    Article  ADS  Google Scholar 

  65. Starr, F. W., Douglas, J. F. & Sastry, S. The relationship of dynamical heterogeneity to the Adam-Gibbs and random first-order transition theories of glass formation. J. Chem. Phys. 138, 12A541 (2013).

    Article  Google Scholar 

  66. Garrahan, J. P. Dynamic heterogeneity comes to life. Proc. Natl Acad. Sci. USA 108, 4701–4702 (2011).

    Article  ADS  Google Scholar 

  67. Berthier, L. Dynamic heterogeneity in amorphous materials. Preprint at https://arxiv.org/abs/1106.1739 (2011).

  68. Störzer, M., Gross, P., Aegerter, C. M. & Maret, G. Observation of the critical regime near Anderson localization of light. Phys. Rev. Lett. 96, 063904 (2006).

    Article  ADS  Google Scholar 

  69. Anderson, P. W. Absence of diffusion in certain random lattices. Phys. Rev. 109, 1492 (1958).

    Article  ADS  Google Scholar 

  70. Segev, M., Silberberg, Y. & Christodoulides, D. N. Anderson localization of light. Nat. Photon. 7, 197–204 (2013).

    Article  ADS  Google Scholar 

  71. Wiersma, D. S. Disordered photonics. Nat. Photon. 7, 188–196 (2013).

    Article  ADS  Google Scholar 

  72. Sun, Z. G. et al. Cofilin-mediated actin filament network flexibility facilitates 2D to 3D actomyosin shape change. Eur. J. Cell Biol. 103, 151379 (2024).

    Article  Google Scholar 

  73. Van Hove, L. Correlations in space and time and Born approximation scattering in systems of interacting particles. Phys. Rev. 95, 249 (1954).

    Article  ADS  MathSciNet  Google Scholar 

  74. Hohenberg, P. C. & Halperin, B. I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 49, 435 (1977).

    Article  ADS  Google Scholar 

  75. Fisher, M. E. Renormalization group theory: its basis and formulation in statistical physics. Rev. Mod. Phys. 70, 653 (1998).

    Article  ADS  MathSciNet  Google Scholar 

  76. Bouchaud, J.-P. & Georges, A. Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications. Phys. Rep. 195, 127–293 (1990).

    Article  ADS  MathSciNet  Google Scholar 

  77. Finer, J. T., Simmons, R. M. & Spudich, J. A. Single myosin molecule mechanics: piconewton forces and nanometre steps. Nature 368, 113–119 (1994).

    Article  ADS  Google Scholar 

  78. Molloy, J., Burns, J., Kendrick-Jones, J., Tregear, R. & White, D. Movement and force produced by a single myosin head. Nature 378, 209–212 (1995).

    Article  ADS  Google Scholar 

  79. Kwak, S. G. & Kim, J. H. Central limit theorem: the cornerstone of modern statistics. Korean J. Anesthesiol. 70, 144–156 (2017).

    Article  Google Scholar 

  80. Kumar, N., Singh, S. & Yadav, A. C. Linking space-time correlations for a class of self-organized critical systems. Phys. Rev. E 104, 064132 (2021).

    Article  ADS  MathSciNet  Google Scholar 

  81. Feder, H. J. S. & Feder, J. Self-organized criticality in a stick-slip process. Phys. Rev. Lett. 66, 2669 (1991).

    Article  ADS  Google Scholar 

  82. Shi, Y. Dissecting Cytoskeletal Dynamics with Active Micropost Arrays. PhD thesis, Johns Hopkins Univ. (2020).

  83. Chen, J., Chen, H., Cai, X., Weng, P. & Nie, H. Parameter estimation of stable distribution based on zero-order statistics. AIP Conf. Proc. 1864, 020171 (2017).

  84. Samorodnitsky, G., Taqqu, M. S. & Linde, R. Stable non-Gaussian random processes: stochastic models with infinite variance. Bull. Lond. Math. Soc. 28, 554–555 (1996).

    Article  Google Scholar 

  85. Zolotarev, V. M. One-Dimensional Stable Distributions (American Mathematical Soc., 1986).

  86. Metzler, R. & Klafter, J. The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 339, 1–77 (2000).

    Article  ADS  MathSciNet  Google Scholar 

  87. Murrell, M. & Gardel, M. L. Actomyosin sliding is attenuated in contractile biomimetic cortices. Mol. Biol. Cell 25, 1845–1853 (2014).

    Article  Google Scholar 

  88. MacKintosh, F. C. & Levine, A. J. Nonequilibrium mechanics and dynamics of motor-activated gels. Phys. Rev. Lett. 100, 018104 (2008).

    Article  ADS  Google Scholar 

  89. Reis, P. M., Ingale, R. A. & Shattuck, M. D. Caging dynamics in a granular fluid. Phys. Rev. Lett. 98, 188301 (2007).

    Article  ADS  Google Scholar 

  90. Weeks, E. R., Crocker, J. C., Levitt, A. C., Schofield, A. & Weitz, D. A. Three-dimensional direct imaging of structural relaxation near the colloidal glass transition. Science 287, 627–631 (2000).

    Article  ADS  Google Scholar 

  91. Guo, M. et al. Probing the stochastic, motor-driven properties of the cytoplasm using force spectrum microscopy. Cell 158, 822–832 (2014).

    Article  Google Scholar 

  92. Gal, N., Lechtman-Goldstein, D. & Weihs, D. Particle tracking in living cells: a review of the mean square displacement method and beyond. Rheol. Acta 52, 425–443 (2013).

    Article  Google Scholar 

  93. Weirich, K. L., Stam, S., Munro, E. & Gardel, M. L. Actin bundle architecture and mechanics regulate myosin II force generation. Biophys. J. 120, 1957–1970 (2021).

    Article  ADS  Google Scholar 

  94. Kaminer, B. & Bell, A. L. Myosin filamentogenesis: effects of pH and ionic concentration. J. Mol. Biol. 20, 391–401 (1966).

    Article  Google Scholar 

  95. Popov, K., Komianos, J. & Papoian, G. A. MEDYAN: mechanochemical simulations of contraction and polarity alignment in actomyosin networks. PLoS Comput. Biol. 12, e1004877 (2016).

    Article  ADS  Google Scholar 

  96. Sheiko, S. S. et al. Adsorption-induced scission of carbon–carbon bonds. Nature 440, 191–194 (2006).

    Article  ADS  Google Scholar 

  97. Lutz, J.-F., Lehn, J.-M., Meijer, E. & Matyjaszewski, K. From precision polymers to complex materials and systems. Nat. Rev. Mater. 1, 16024 (2016).

    Article  ADS  Google Scholar 

  98. Li, Z. et al. Bottlebrush polymers: from controlled synthesis, self-assembly, properties to applications. Prog. Polym. Sci. 116, 101387 (2021).

    Article  Google Scholar 

  99. Cardamone, L., Laio, A., Torre, V., Shahapure, R. & DeSimone, A. Cytoskeletal actin networks in motile cells are critically self-organized systems synchronized by mechanical interactions. Proc. Natl Acad. Sci. USA 108, 13978–13983 (2011).

    Article  ADS  Google Scholar 

  100. Deriu, M. A. et al. Biomechanics of actin filaments: a computational multi-level study. J. Biomech. 44, 630–636 (2011).

    Article  Google Scholar 

  101. Murphy, N., Wortis, R. & Atkinson, W. Generalized inverse participation ratio as a possible measure of localization for interacting systems. Phys. Rev. B 83, 184206 (2011).

    Article  ADS  Google Scholar 

  102. Rizzo, T. & Tarzia, M. Localized phase of the Anderson model on the Bethe lattice. Phys. Rev. B 110, 184210 (2024).

    Article  Google Scholar 

  103. Bueno, C., Liman, J., Schafer, N. P., Cheung, M. S. & Wolynes, P. G. A generalized Flory-Stockmayer kinetic theory of connectivity percolation and rigidity percolation of cytoskeletal networks. PLoS Comput. Biol. 18, e1010105 (2022).

    Article  ADS  Google Scholar 

  104. Pollard, T. D. & Borisy, G. G. Cellular motility driven by assembly and disassembly of actin filaments. Cell 112, 453–465 (2003).

    Article  Google Scholar 

  105. Mullins, R. D., Heuser, J. A. & Pollard, T. D. The interaction of Arp2/3 complex with actin: nucleation, high affinity pointed end capping, and formation of branching networks of filaments. Proc. Natl Acad. Sci. USA 95, 6181–6186 (1998).

    Article  ADS  Google Scholar 

  106. Dalton, F. & Corcoran, D. Self-organized criticality in a sheared granular stick-slip system. Phys. Rev. E 63, 061312 (2001).

    Article  ADS  Google Scholar 

  107. Rodríguez-Cruz, C. et al. Experimental observations of fractal landscape dynamics in a dense emulsion. Soft Matter 19, 6805–6813 (2023).

    Article  ADS  Google Scholar 

  108. Alvarado, J., Sheinman, M., Sharma, A., MacKintosh, F. C. & Koenderink, G. H. Molecular motors robustly drive active gels to a critically connected state. Nat. Phys. 9, 591–597 (2013).

    Article  Google Scholar 

  109. Tsuda, Y., Yasutake, H., Ishijima, A. & Yanagida, T. Torsional rigidity of single actin filaments and actin–actin bond breaking force under torsion measured directly by in vitro micromanipulation. Proc. Natl Acad. Sci. USA 93, 12937–12942 (1996).

    Article  ADS  Google Scholar 

  110. Basko, D. M., Aleiner, I. L. & Altshuler, B. L. Metal–insulator transition in a weakly interacting many-electron system with localized single-particle states. Ann. Phys. 321, 1126–1205 (2006).

    Article  ADS  Google Scholar 

  111. Chan, C., Beltzner, C. C. & Pollard, T. D. Cofilin dissociates Arp2/3 complex and branches from actin filaments. Curr. Biol. 19, 537–545 (2009).

    Article  Google Scholar 

  112. Pandit, N. G. et al. Force and phosphate release from Arp2/3 complex promote dissociation of actin filament branches. Proc. Natl Acad. Sci. USA 117, 13519–13528 (2020).

    Article  ADS  Google Scholar 

  113. Jung, W., Murrell, M. P. & Kim, T. F-actin fragmentation induces distinct mechanisms of stress relaxation in the actin cytoskeleton. Biophys. J. 110, 354a (2016).

    Article  Google Scholar 

  114. Andrianantoandro, E. & Pollard, T. D. Mechanism of actin filament turnover by severing and nucleation at different concentrations of ADF/cofilin. Mol. Cell 24, 13–23 (2006).

    Article  Google Scholar 

  115. Wioland, H. et al. ADF/cofilin accelerates actin dynamics by severing filaments and promoting their depolymerization at both ends. Curr. Biol. 27, 1956–1967. e1957 (2017).

    Article  Google Scholar 

  116. Lappalainen, P. & Drubin, D. G. Cofilin promotes rapid actin filament turnover in vivo. Nature 388, 78–82 (1997).

    Article  ADS  Google Scholar 

  117. Zhang, X.-F. et al. Regulation of axon growth by myosin II–dependent mechanocatalysis of cofilin activity. J. Cell Biol. 218, 2329–2349 (2019).

    Article  Google Scholar 

  118. Jung, W. et al. Dynamic motions of molecular motors in the actin cytoskeleton. Cytoskeleton 76, 517–531 (2019).

    Article  Google Scholar 

  119. Bertling, E. et al. Cyclase-associated protein 1 (CAP1) promotes cofilin-induced actin dynamics in mammalian nonmuscle cells. Mol. Biol. cell 15, 2324–2334 (2004).

    Article  Google Scholar 

  120. Kotila, T. et al. Structural basis of actin monomer re-charging by cyclase-associated protein. Nat. Commun. 9, 1892 (2018).

    Article  ADS  Google Scholar 

  121. Chaudhry, F. et al. Srv2/cyclase-associated protein forms hexameric shurikens that directly catalyze actin filament severing by cofilin. Mol. Biol. Cell 24, 31–41 (2013).

    Article  Google Scholar 

  122. Alimov, N., Hoeprich, G. J., Padrick, S. B. & Goode, B. L. Cyclase-associated protein interacts with actin filament barbed ends to promote depolymerization and formin displacement. J. Biol. Chem. 299, 105367 (2023).

    Article  Google Scholar 

  123. Guo, S., Hoeprich, G. J., Magliozzi, J. O., Gelles, J. & Goode, B. L. Dynamic remodeling of actin networks by cyclase-associated protein and CAP-Abp1 complexes. Curr. Biol. 33, 4484–4495.e4485 (2023).

    Article  Google Scholar 

  124. Yu, Q., Li, J., Murrell, M. P. & Kim, T. Balance between force generation and relaxation leads to pulsed contraction of actomyosin networks. Biophys. J. 115, 2003–2013 (2018).

    Article  ADS  Google Scholar 

  125. Vidiella, B. et al. Engineering self-organized criticality in living cells. Nat. Commun. 12, 4415 (2021).

    Article  ADS  Google Scholar 

  126. Walleczek J. Self-Organized Biological Dynamics and Nonlinear Control: Toward Understanding Complexity, Chaos and Emergent Function in Living Systems (Cambridge Univ. Press, 2006).

  127. Kim, T., Hwang, W., Lee, H. & Kamm, R. D. Computational analysis of viscoelastic properties of crosslinked actin networks. PLoS Comput. Biol. 5, e1000439 (2009).

    Article  ADS  Google Scholar 

  128. Luan, Y., Lieleg, O., Wagner, B. & Bausch, A. R. Micro- and macrorheological properties of isotropically cross-linked actin networks. Biophys. J. 94, 688–693 (2008).

    Article  ADS  Google Scholar 

  129. Lieleg, O., Claessens, M. M. & Bausch, A. R. Structure and dynamics of cross-linked actin networks. Soft Matter 6, 218–225 (2010).

    Article  ADS  Google Scholar 

  130. Sun, Z. G. & Murrell, M. Cofilin-mediated filament softening and crosslinking counterbalance to enhance actin network flexibility. Phys. Rev. Lett. 133, 218402 (2024).

    Article  Google Scholar 

  131. Shin, J. H., Gardel, M., Mahadevan, L., Matsudaira, P. & Weitz, D. Relating microstructure to rheology of a bundled and cross-linked F-actin network in vitro. Proc. Natl Acad. Sci. USA 101, 9636–9641 (2004).

    Article  ADS  Google Scholar 

  132. Gardel, M. L. et al. Elastic behavior of cross-linked and bundled actin networks. Science 304, 1301–1305 (2004).

    Article  ADS  Google Scholar 

  133. Gardel, M. L. et al. Prestressed F-actin networks cross-linked by hinged filamins replicate mechanical properties of cells. Proc. Natl Acad. Sci. USA 103, 1762–1767 (2006).

    Article  ADS  Google Scholar 

  134. Gardel, M. et al. Scaling of F-actin network rheology to probe single filament elasticity and dynamics. Phys. Rev. Lett. 93, 188102 (2004).

    Article  ADS  Google Scholar 

  135. Verkhovsky, A. B. & Borisy, G. G. Non-sarcomeric mode of myosin II organization in the fibroblast lamellum. J. Cell Biol. 123, 637–652 (1993).

    Article  Google Scholar 

  136. Miura, K. Bleach correction ImageJ plugin for compensating the photobleaching of time-lapse sequences. F1000Res. 9, 1494 (2020).

    Article  Google Scholar 

Download references

Acknowledgements

We are grateful for insightful discussions with C. O’Hern, M. Shattuck and J. (J.) Treado. We acknowledge the initial contribution related to this project by C. Muresan, A. Pasha Tabatabai and L. Lanier. This work was supported by funding through ARO MURI W911NF-14-1-0403, National Institutes of Health (NIH) R01 1R01GM126256, NIH U54 CA209992 and Human Frontiers Science Program (HFSP) grant no. RGY0073/2018 to M.M. We acknowledge the University of Maryland supercomputing resources (https://hpcc.umd.edu) made available for conducting the computational research reported in this paper.

Author information

Authors and Affiliations

  1. Department of Physics, Yale University, New Haven, CT, USA

    Zachary Gao Sun & Michael Murrell

  2. Systems Biology Institute, Yale University, West Haven, CT, USA

    Zachary Gao Sun & Michael Murrell

  3. Integrated Graduate Program in Physical and Engineering Biology, Yale University, New Haven, CT, USA

    Zachary Gao Sun & Michael Murrell

  4. Institute for Physical Science and Technology, University of Maryland, College Park, MD, USA

    Nathan Zimmerberg & Patrick Kelly

  5. Biophysics Program, University of Maryland, College Park, MD, USA

    Nathan Zimmerberg

  6. Chemical Physics Program, University of Maryland, College Park, MD, USA

    Patrick Kelly

  7. The James Franck Institute, The University of Chicago, Chicago, IL, USA

    Carlos Floyd

  8. Department of Chemistry and Biochemistry, University of Maryland, College Park, MD, USA

    Garegin Papoian

  9. Department of Biomedical Engineering, Yale University, New Haven, CT, USA

    Michael Murrell

Authors
  1. Zachary Gao Sun
    View author publications

    Search author on:PubMed Google Scholar

  2. Nathan Zimmerberg
    View author publications

    Search author on:PubMed Google Scholar

  3. Patrick Kelly
    View author publications

    Search author on:PubMed Google Scholar

  4. Carlos Floyd
    View author publications

    Search author on:PubMed Google Scholar

  5. Garegin Papoian
    View author publications

    Search author on:PubMed Google Scholar

  6. Michael Murrell
    View author publications

    Search author on:PubMed Google Scholar

Contributions

Z.G.S. and M.M. designed and conceived the work and drafted the paper. Z.G.S., M.M., C.F. and N.Z. edited the paper. Z.G.S. performed the experiments. Z.G.S. analysed the experimental data. N.Z. and P.K. performed the simulations. Z.G.S., N.Z. and P.K. analysed the simulation data. M.M. and G.P. supervised the work.

Corresponding author

Correspondence to Michael Murrell.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Yu Shi and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figs. 1–14, description of the simulation model and captions for Supplementary Videos.

Reporting Summary

Supplementary Video 1

0.74-nM Arp2/3-nucleated F-actin deformed by MTFs.

Supplementary Video 2

0.74-nM Arp2/3-nucleated F-actin deformed by MTF composite.

Supplementary Video 3

MEDYAN simulation of Rarp = 0.002 F-actin deformed by MTFs.

Supplementary Video 4

MEDYAN simulation of Rarp = 0.02 F-actin deformed by MTFs.

Supplementary Video 5

MEDYAN simulation of Rarp = 0.004 F-actin filament large bending by MTFs.

Supplementary Video 6

MEDYAN simulation of Rarp = 0.02 F-actin filament large bending by MTFs.

Supplementary Video 7

MEDYAN simulation of Rarp = 0.02 F-actin filament large displacements and energy release over time.

Source data

Source Data Figs. 1–5

Source data for Figs. 1–5.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sun, Z.G., Zimmerberg, N., Kelly, P. et al. Feedback between F-actin organization and active stress governs criticality and energy localization in the cell cytoskeleton. Nat. Phys. 21, 1290–1302 (2025). https://doi.org/10.1038/s41567-025-02919-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-025-02919-4

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing