Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Experimental demonstration of breakeven for a compact fermionic encoding

Nature Physics volume 21, pages 1319–1325 (2025)Cite this article

Subjects

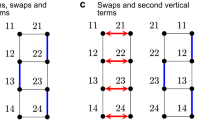
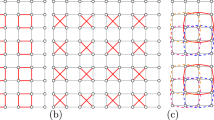
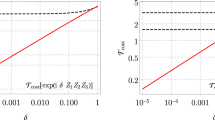
Abstract

Solving the Fermi–Hubbard model is a central task in the study of strongly correlated materials. Digital quantum computers can, in principle, be suitable for this purpose, but have so far been limited to quasi-one-dimensional models. This is because of exponential overheads caused by the interplay of noise and the non-locality of the mapping between fermions and qubits. Here we use a trapped-ion quantum computer to experimentally demonstrate that a recently developed local encoding can overcome this problem. In particular, we show that suitable reordering of terms and application of circuit identities—a scheme called corner hopping—substantially reduces the cost of simulating fermionic hopping. This enables the efficient preparation of the ground state of a 6 × 6 spinless Fermi–Hubbard model encoded in 48 physical qubits. We also develop two error mitigation schemes for systems with conserved quantities, based on local postselection and on extrapolation of local observables, respectively. Our results suggest that Fermi–Hubbard models beyond classical simulability can be addressed by digital quantum computers without large increases in gate fidelity.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Simulating fermions with a trapped-ion quantum computer.
Fig. 2: The Fermi–Hubbard model and the two fermion-to-qubit mappings implemented in this work.
Fig. 3: Raw data for the adiabatic evolution.
Fig. 4: ‘Corner-hopping’ compilation scheme for simulating the hopping operator in the compact encoding.
Fig. 5: Error mitigation and sensitivity to noise in the JW encoding.
Fig. 6: Physical properties of the prepared state.

Similar content being viewed by others

Data availability

The numerical data that support the findings of this study, including a full list of shots, are available via Zenodo at https://doi.org/10.5281/zenodo.13624900 (ref. 47). Source data are provided with this paper.

References

  1. Arovas, D. P., Berg, E., Kivelson, S. A. & Raghu, S. The Hubbard model. Annu. Rev. Condens. Matter Phys. 13, 239 (2022).

    Article  ADS  Google Scholar 

  2. Qin, M., Schäfer, T., Andergassen, S., Corboz, P. & Gull, E. The Hubbard model: a computational perspective. Annu. Rev. Condens. Matter Phys. 13, 275–302 (2022).

    Article  ADS  Google Scholar 

  3. Wilson, J. A., Di Salvo, F. J. & Mahajan, S. Charge-density waves in metallic, layered, transition-metal dichalcogenides. Phys. Rev. Lett. 32, 882 (1974).

    Article  ADS  Google Scholar 

  4. Bednorz, J. G. & Müller, K. A. Possible highTc superconductivity in the BaLaCuO system. Zeitschrift für Physik B 64, 189–193 (1986).

    Article  ADS  Google Scholar 

  5. Takada, K. et al. Superconductivity in two-dimensional CoO2 layers. Nature 422, 53–55 (2003).

    Article  ADS  Google Scholar 

  6. Catalano, S. et al. Rare-earth nickelates RNiO3: thin films and heterostructures. Rep. Prog. Phys. 81, 046501 (2018).

    Article  ADS  MathSciNet  Google Scholar 

  7. Wu, F., Lovorn, T., Tutuc, E. & MacDonald, A. Hubbard model physics in transition metal dichalcogenide Moire bands. Phys. Rev. Lett. 121, 026402 (2018).

    Article  ADS  Google Scholar 

  8. Ponsioen, B., Chung, S. S. & Corboz, P. Period 4 stripe in the extended two-dimensional Hubbard model. Phys. Rev. B 100, 195141 (2019).

    Article  ADS  Google Scholar 

  9. Xu, H. et al. Coexistence of superconductivity with partially filled stripes in the Hubbard model. Science https://doi.org/10.1126/science.adh7691 (2024).

  10. Ray, S. & Werner, P. Photoinduced ferromagnetic and superconducting orders in multiorbital Hubbard models. Phys. Rev. B 110, L041109 (2024).

    Article  Google Scholar 

  11. Zhang, Y., Mondaini, R. & Scalettar, R. T. Photoinduced enhancement of superconductivity in the plaquette Hubbard model. Phys. Rev. B 107, 064309 (2023).

    Article  ADS  Google Scholar 

  12. Kaneko, T., Shirakawa, T., Sorella, S. & Yunoki, S. Photoinduced eta-pairing in the Hubbard model. Phys. Rev. Lett. 122, 077002 (2019).

    Article  ADS  Google Scholar 

  13. White, I. G., Hulet, R. G. & Hazzard, K. R. A. Correlations generated from high-temperature states: nonequilibrium dynamics in the Fermi–Hubbard model. Phys. Rev. A 100, 033612 (2019).

    Article  ADS  Google Scholar 

  14. Mehio, O. et al. A Hubbard exciton fluid in a photo-doped antiferromagnetic Mott insulator. Nat. Phys. https://doi.org/10.1038/s41567-023-02204-2 (2023).

  15. Fava, S. et al. Magnetic field expulsion in optically driven YBa2Cu3O6.48. Nature 632, 75–80 (2024).

    Article  Google Scholar 

  16. Mitra, D. et al. Quantum gas microscopy of an attractive Fermi–Hubbard system. Nat. Phys. 14, 173–177 (2018).

    Article  Google Scholar 

  17. Bakr, W. S., Gillen, J. I., Peng, A., Fölling, S. & Greiner, M. A quantum gas microscope for detecting single atoms in a Hubbard-regime optical lattice. Nature 462, 74–77 (2009).

    Article  ADS  Google Scholar 

  18. Greif, D., Uehlinger, T., Jotzu, G., Tarruell, L. & Esslinger, T. Short-range quantum magnetism of ultracold fermions in an optical lattice. Science 340, 1307–1310 (2013).

    Article  ADS  Google Scholar 

  19. Hilker, T. A. et al. Revealing hidden antiferromagnetic correlations in doped Hubbard chains via string correlators. Science 357, 484–487 (2017).

    Article  ADS  MathSciNet  Google Scholar 

  20. Mazurenko, A. et al. A cold-atom Fermi–Hubbard antiferromagnet. Nature 545, 462–466 (2017).

    Article  ADS  Google Scholar 

  21. Stanisic, S. et al. Observing ground-state properties of the Fermi–Hubbard model using a scalable algorithm on a quantum computer. Nat. Commun. 13, 5743 (2022).

    Article  ADS  Google Scholar 

  22. Hémery, K. et al. Measuring the Loschmidt amplitude for finite-energy properties of the Fermi–Hubbard model on an ion-trap quantum computer. PRX Quantum 5, 030323 (2024).

    Article  Google Scholar 

  23. Arute, F. et al. Observation of separated dynamics of charge and spin in the Fermi–Hubbard model. Preprint at https://arxiv.org/abs/2010.07965 (2020).

  24. Jordan, P. & Wigner, E. Über das Paulische Äquivalenzverbot. Zeitschrift für Physik 47, 631–651 (1928).

    Article  ADS  Google Scholar 

  25. Kivlichan, I. D. et al. Quantum simulation of electronic structure with linear depth and connectivity. Phys. Rev. Lett. 120, 110501 (2018).

    Article  ADS  MathSciNet  Google Scholar 

  26. Granet, E. & Dreyer, H. Dilution of error in digital Hamiltonian simulation. PRX Quantum 6, 010333 (2025).

    Article  Google Scholar 

  27. Chertkov, E., Chen, Y.-H., Lubasch, M., Hayes, D. & Foss-Feig, M. Robustness of near-thermal dynamics on digital quantum computers. Preprint at https://arxiv.org/abs/2410.10794

  28. Schiffer, B. F., Rubio, A. F., Trivedi, R. & Cirac, J. I. The quantum adiabatic algorithm suppresses the proliferation of errors. Preprint at https://arxiv.org/abs/2404.15397

  29. Derby, C., Klassen, J., Bausch, J. & Cubitt, T. Compact fermion to qubit mappings. Phys. Rev. B 104, 035118 (2021).

    Article  ADS  Google Scholar 

  30. Jafarizadeh, A., Pollmann, F. & Gammon-Smith, A. A recipe for local simulation of strongly-correlated fermionic matter on quantum computers: the 2D Fermi–Hubbard model. Preprint at https://arxiv.org/abs/2408.14543 (2024).

  31. Cade, C., Mineh, L., Montanaro, A. & Stanisic, S. Strategies for solving the Fermi–Hubbard model on near-term quantum computers. Phys. Rev. B 102, 235122 (2020).

    Article  ADS  Google Scholar 

  32. Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information 10th Anniversary edn (Cambridge Univ. Press, 2010).

  33. Hastings, M. B., Wecker, D., Bauer, B. & Troyer, M. Improving quantum algorithms for quantum chemistry. Quantum Info. Comput. 15, 1–21 (2015).

    MathSciNet  Google Scholar 

  34. Moses, S. et al. A race-track trapped-ion quantum processor. Phys. Rev. X 13, 041052 (2023).

    Google Scholar 

  35. DeCross, M. et al. The computational power of random quantum circuits in arbitrary geometries. Phys. Rev. X 15, 021052 (2025).

    Google Scholar 

  36. Bausch, J., Cubitt, T., Derby, C. & Klassen, J. Mitigating errors in local fermionic encodings. Preprint at https://arxiv.org/abs/2003.07125 (2020).

  37. Iqbal, M. et al. Topological order from measurements and feed-forward on a trapped ion quantum computer. Nat. Commun. Phys. 7, 205 (2024).

    Google Scholar 

  38. Foss-Feig, M. et al. Experimental demonstration of the advantage of adaptive quantum circuits. Preprint at https://arxiv.org/abs/2302.03029 (2023).

  39. Xie, Q., Seki, K. & Yunoki, S. Variational counterdiabatic driving of the Hubbard model for ground-state preparation. Phys. Rev. B 106, 155153 (2022).

    Article  ADS  Google Scholar 

  40. Kovalsky, L. K. et al. Self-healing of Trotter error in digital adiabatic state preparation. Phys. Rev. Lett. 131, 060602 (2023).

    Article  ADS  Google Scholar 

  41. Tang, J. et al. Exploring ground states of Fermi–Hubbard model on honeycomb lattices with counterdiabaticity. npj Quantum Mater. 9, 87 (2024).

    Article  Google Scholar 

  42. Schiffer, B. F., Tura, J. & Cirac, J. I. Adiabatic spectroscopy and a variational quantum adiabatic algorithm. PRX Quantum 3, 020347 (2022).

    Article  ADS  Google Scholar 

  43. Derby, C. Compact Fermion to Qubit Mappings for Quantum Simulation. PhD thesis, Univ. College London (2023); https://discovery.ucl.ac.uk/id/eprint/10165683/

  44. Clinton, L. et al. Towards near-term quantum simulation of materials. Nat. Commun. 15, 211 (2024).

    Article  ADS  Google Scholar 

  45. Setia, K., Bravyi, S., Mezzacapo, A. & Whitfield, J. D. Superfast encodings for fermionic quantum simulation. Phys. Rev. Res. 1, 033033 (2019).

    Article  Google Scholar 

  46. Chien, R. W., Setia, K., Bonet-Monroig, X., Steudtner, M. & Whitfield, J. D. Simulating quantum error mitigation in fermionic encodings. Preprint at https://arxiv.org/abs/2303.02270 (2023).

  47. Nigmatullin, R. et al. Supporting data for ‘Experimental demonstration of break-even for the compact fermionic encoding’. Zenodo https://doi.org/10.5281/zenodo.13624900 (2024).

Download references

Acknowledgements

This work was made possible by a large group of people, and we thank the entire Quantinuum team for their many contributions. We are grateful for helpful discussions with and feedback from M. Iqbal, G. Greene-Diniz and S.-H. Lin. E.G. acknowledges support by the Bavarian Ministry of Economic Affairs, Regional Development and Energy (StMWi) under project Bench-QC (grant no. DIK0425/01). K.H. and H.D. acknowledge support by the German Federal Ministry of Education and Research (BMBF) through the project EQUAHUMO (grant no. 13N16069) within the funding programme quantum technologies – from basic research to market. The bulk of the experimental data reported in this work, including all circuits described in Fig. 3, was produced by the Quantinuum H2-1 trapped-ion quantum computer, powered by Honeywell, on 10–14 June 2024.

Author information

Authors and Affiliations

  1. Quantinuum, Munich, Germany

    Ramil Nigmatullin, Kévin Hémery, Khaldoon Ghanem, Etienne Granet & Henrik Dreyer

  2. Quantinuum, Broomfield, CO, USA

    Steven Moses, Dan Gresh, Peter Siegfried, Michael Mills, Thomas Gatterman & Nathan Hewitt

Authors
  1. Ramil Nigmatullin
    View author publications

    Search author on:PubMed Google Scholar

  2. Kévin Hémery
    View author publications

    Search author on:PubMed Google Scholar

  3. Khaldoon Ghanem
    View author publications

    Search author on:PubMed Google Scholar

  4. Steven Moses
    View author publications

    Search author on:PubMed Google Scholar

  5. Dan Gresh
    View author publications

    Search author on:PubMed Google Scholar

  6. Peter Siegfried
    View author publications

    Search author on:PubMed Google Scholar

  7. Michael Mills
    View author publications

    Search author on:PubMed Google Scholar

  8. Thomas Gatterman
    View author publications

    Search author on:PubMed Google Scholar

  9. Nathan Hewitt
    View author publications

    Search author on:PubMed Google Scholar

  10. Etienne Granet
    View author publications

    Search author on:PubMed Google Scholar

  11. Henrik Dreyer
    View author publications

    Search author on:PubMed Google Scholar

Contributions

R.N. designed the adiabatic path, generated all circuits, carried out a large part of the data analysis and invented the local stabilizer filtering technique. K.H. performed many of the classical statevector and matrix product state calculations. S.M., D.G., P.S., M.M., T.G. and N.H. built the experiment and took the data. K.G., R.N. and K.H. made a library that was heavily used to automatically visualize and create circuits from fermionic encodings specified by edge and vertex operators. E.G. contributed to the theory of the stabilizer-based zero noise extrapolation as well as the visualization. R.N., K.H., K.G., E.G. and H.D. conceived the experimental design. H.D. contributed to the compilation scheme, data analysis and initial hypothesis and drafted the initial manuscript, to which all authors contributed.

Corresponding author

Correspondence to Henrik Dreyer.

Ethics declarations

Competing interests

H.D. is a shareholder of Quantinuum. The other authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks James Whitfield and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figs. 1–15, Discussion and Tables 1 and 2.

Source data

Source Data Fig. 4

As requested, data for all panels in Fig. 4 merged in one file. Contains data for all panels with data, namely, Fig. 4b (Energy density vs number of Trotter layers on 4 × 4), 4c (Energy density vs number of Trotter layers on 6 × 6) and 4d (Signal attenuation vs system size).

Source Data Fig. 5

As requested, data for all panels in Fig. 5 merged in one file. Contains data for all panels with data, namely, Fig. 5a (Energy densities of initial and final states), 5b (Temperature corresponding to energy density in a), 5c (Charge-density correlations for the state created using Jordan–Wigner) and 5d (Charge-density correlations for the state created using the compact encoding).

Source Data Fig. 6

As requested, data for all panels in Fig. 6 merged in one file. Contains data for all panels with data, namely, Fig. 6e (The amount of noise on observables with different weight in the Jordan–Wigner encoding), 6f (The Coulomb energy density in the compact encoding with and without global filtering error mitigation) and 6g (Coulomb energy density output of different noise mitigation schemes and their associated retained bit rates).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nigmatullin, R., Hémery, K., Ghanem, K. et al. Experimental demonstration of breakeven for a compact fermionic encoding. Nat. Phys. 21, 1319–1325 (2025). https://doi.org/10.1038/s41567-025-02931-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41567-025-02931-8

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing