Abstract
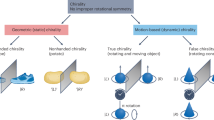
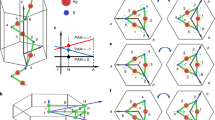
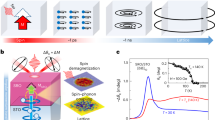
In condensed matter, angular momentum is intimately related to the emergence of topological quantum states, including chiral superconductivity, quantum spin liquids and various chiral quasiparticles. Recently, it has been predicted that microscopic lattice excitations, known as phonons, can carry finite angular momentum, leading to specific physical properties of materials. However, phonon angular momentum has not yet been observed directly. Here we demonstrate that angular momentum conservation results in a macroscopic mechanical torque when applying a time-reversal symmetry-breaking thermal gradient along the chiral axis of single-crystal tellurium. We probe this torque using a cantilever-based device and establish that it changes sign by flipping the chirality or thermal gradient. This behavior disappears in polycrystalline samples that lack a preferred chirality. Our experimental results align well with theoretical calculations. We provide compelling evidence for phonon angular momentum, which might enable quantum states with potential applications in microelectronics.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding authors upon request. Source data are provided with this paper.
References
Einstein, A. & de Haas, W. J. Experimental proof of the existence of Ampère’s molecular currents. KNAW Proc. 18, 696–711 (1915).
Scott, G. G. Review of gyromagnetic ratio experiments. Rev. Mod. Phys. 34, 102–109 (1962).
Zhang, L. F. & Niu, Q. Angular momentum of phonons and the Einstein–de Haas effect. Phys. Rev. Lett. 112, 085503 (2014).
Hamada, M., Minamitani, E., Hirayama, M. & Murakami, S. Phonon angular momentum induced by the temperature gradient. Phys. Rev. Lett. 121, 175301 (2018).
Romao, C. P., Catena, R., Spaldin, N. A. & Matas, M. Chiral phonons as dark matter detectors. Phys. Rev. Res. 5, 043262 (2023).
Ren, Y. F., Xiang, C., Saparov, D. & Niu, Q. Phonon magnetic moment from electronic topological magnetization. Phys. Rev. Lett. 127, 186403 (2021).
Kim, K. et al. Chiral phonon activated spin Seeback effect. Nat. Mater. 22, 322–328 (2023).
Basini, M. et al. Terahertz electric-field-driven dynamical multiferroicity in SrTiO3. Nature 628, 534–539 (2024).
Ohe, K. et al. Chirality-induced selectivity of phonon angular momentum in chiral quartz crystals. Phys. Rev. Lett. 132, 056302 (2024).
Chen et al. Chiral phonon diode effect in chiral cystals. Nano Lett. 4, 1688–1693 (2022).
Liu, M. et al. Light-driven nanoscale plasmonic motors. Nat. Nanotech. 5, 570–573 (2010).
Zhang, T. T., Murakami, S. & Miao, H. Topological and chiral phonons. Nat. Commun. 16, 3560 (2025).
Zhang, T. T., Liu, Y., Miao, H. & Murakami, S. New advances in phonons: from band topology to quasiparticle chirality. Preprint at https://arxiv.org/abs/2505.06179 (2025).
Alfonsov, A., Büchner, B. & Kataev, V. All-on-chip concurrent measurements of the static magnetization and of the electron spin resonance with microcantilevers. Appl. Magn. Reson. 53, 555–563 (2022).
Fukuroi, T. & Muto, Y. Specific heat of tellurium and selenium at very low temperatures. Chem. Metall. 8, 213–222 (1956).
Edelstein, V. M. Spin polarization of conduction electrons induced by electric current in two-dimensional asymmetric electron systems. Solid State Commun. 73, 233–235 (1990).
Tang, F. et al. Three-dimensional quantum Hall effect and metal–insulator transition in ZrTe5. Nature 569, 537–541 (2019).
Gooth, J. et al. Axionic charge density wave in the Weyl semimetal (TaSe4)2I. Nature 575, 315–319 (2019).
Miao, H. et al. Spontaneous chirality flipping in an orthogonal spin-charged ordered topological magnet. Phys. Rev. X 14, 011053 (2024).
Yang, F., et al. Incommensurate transverse Peierls transition. Preprint at https://arxiv.org/abs/2410.10539 (2024).
Tauchert, S. R. et al. Polarized phonons carry angular momentum in ultrafast demagnetization. Nature 602, 73–77 (2022).
Choi, I. H. et al. Real-time dynamics of angular momentum transfer from spin to acoustic chiral phonon in oxide heterostructures. Nat. Nanotech. 19, 1277–1282 (2024).
Grissonnanche, G. et al. Chiral phonons in the pseudogap phase of cuprates. Nat. Phys. 16, 1108–1111 (2020).
Kasahara, Y. et al. Majorana quantization and half-integer thermal quantum Hall effect in a Kitaev spin liquid. Nature 559, 227–231 (2018).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Rao, Z. et al. Observation of unconventional chiral fermions with long Fermi arcs in CoSi. Nature 567, 496–499 (2019).
Šmejkal, L. et al. Chiral magnons in altermagnetic RuO2. Phys. Rev. Lett. 131, 256703 (2023).
Park, S. & Yang, B.-J. Phonon angular momentum Hall effect. Nano Lett. 20, 7694–7699 (2020).
Wen, X. G., Wilczek, F. & Zee, A. Chiral spin states and superconductivity. Phys. Rev. B 39, 11413 (1989).
Kitaev, A. Y. Anyons in an exactly solved model and beyond. Ann. Phys. 321, 2–111 (2006).
Ideue, T. et al. Pressure-induced topological phase transition in noncentrosymmetric element tellurium. Proc. Natl Acad. Sci. USA 116, 25530 (2019).
Koma, A. & Tanaka, S. Etch pits and crystal structure of tellurium. Phys. Stat. Sol. 40, 239–248 (1970).
Ades, S. & Champnes, C. H. Optical activity of tellurium to 20 μm. J. Opt. Soc. Am. 65, 217–218 (1975).
Furukawa, T. et al. Current induced magnetization caused by crystal chirality in nonmagnetic elemental tellurium. Phys. Rev. Res. 3, 023111 (2021).
Spirito, D., Marras, S. & Martin-Garcia, B. Lattice dynamics in chiral tellurium by linear and circularly polarized Raman spectroscopy: crystal orientation and handedness. J. Mater. Chem. C 12, 2544 (2024).
Streib, S. Difference between angular momentum and pseudoangular momentum. Phys. Rev. B 103, L100409 (2021).
Zhang, L. & Niu, Q. Chiral phonons at high-symmetry points in monolayer hexagonal lattices. Phys. Rev. Lett. 115, 115502 (2015).
Zhang, T. & Murakami, S. Chiral phonons and pseudoangular momentum in nonsymmorphic systems. Phys. Rev. Res. 4, L012024 (2022).
Zhu, H. et al. Observation of chiral phonons. Science 359, 579 (2018).
Miao, H. et al. Observation of double Weyl phonons in parity-breaking FeSi. Phys. Rev. Lett. 121, 035302 (2018).
Ishito, K. et al. Truly chiral phonons in α-HgS. Nat. Phys. 19, 35–39 (2023).
Ueda, H. et al. Chiral phonons in quartz probed by x-rays. Nature 618, 946–950 (2023).
Acknowledgements
We thank A. Christianson, C. Hua, R. Hermann, A. May, M. McGuire, B. Sales, R. Zhang and T. Zhang for stimulating discussions. This research (torque measurement, crystal growth and part of the numerical calculations) was supported by the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. N.P. and Y.Z. (numerical calculations) were supported by the Max Planck Partner laboratory for quantum materials of the Max Planck Institute Chemical Physics of Solids.
Author information
Authors and Affiliations
Contributions
H.M. conceived of the project. H.Z. designed and performed the experiments with help from F.Y., T.Z.W., J.-Q.Y. and H.M. N.P. and Y.Z. performed the theoretical calculations. H.Z., P.R., L.L., C.F., Y.Z., J.-Q.Y. and H.M. analysed and interpreted the experimental data. H.Z., Y.Z. and H.M. wrote the paper with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Chirality of Te single crystals.
Etching image on fresh surfaces of right-handed (a) and left-handed (b) Te samples for the torque measurements. Red and cyan ‘4-shaped’ polygons represent characteristic features for right- and left-handed Te single crystals, respectively.
Extended Data Fig. 2 Calibration of temperature gradient.
(a) A typical pulse of sample temperature measurement in the dummy-setup. (b) The measured temperature gradient at various temperatures for the dummy-setup. (c) The calculated \(\nabla\)T for the cantilever-setup. The power density, \(J=\left(\frac{{\rm{P}}}{{\rm{A}}}\right)\), where P and A stand for the laser power and sample cross-area, respectively.
Extended Data Fig. 3 Torque response of right-handed Te single crystal.
Position dependent scan of thermally activated torque response for a right-handed Te single crystal.
Extended Data Fig. 4 Laser power (P) dependence of τ.
Cantilevers 1 and 2 show opposite torque. The magnitude of ∆τ approximately follows a linear dependence of laser power and consistent with the theoretical estimation of Eq. (4), δJph∝∆T.
Supplementary information
Source data
Source Data Fig. 2
Statistical source data.
Source Data Fig. 3
Statistical source data.
Source Data Extended Data Fig./Table 2
Statistical source data.
Source Data Extended Data Fig./Table 3
Statistical source data.
Source Data Extended Data Fig./Table 4
Statistical source data.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zhang, H., Peshcherenko, N., Yang, F. et al. Measurement of phonon angular momentum. Nat. Phys. 21, 1387–1391 (2025). https://doi.org/10.1038/s41567-025-02952-3
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41567-025-02952-3