Elastic properties of force-transmitting linkages determine multistable mechanosensitive behaviour of cell adhesion

Abstract

Cells can sense and respond to their environment. Central to this process is the formation of molecular clutches, which are dynamic linkages between the extracellular matrix and the actin cytoskeleton mediated by integrins and adaptor proteins. Although it is well known that force-dependent interactions between molecular-clutch components are essential for sensing substrate rigidity, the influence of nonlinear adaptor-protein elasticity is poorly understood. Here we show that adaptor-protein elasticity and local interactions between molecular clutches and the extracellular matrix are key to cellular perception of substrate stiffness. We present a semi-analytical theory that integrates experimentally measured force responses of adaptor proteins to describe cell-adhesion sensing. We propose that molecular clutches probe local mechanical substrate properties and collectively function as a differential that allows a retrograde actin flow and substrate movement to occur at different rates while maintaining a stable mechanical coupling between them. Our model reproduces experimentally measured force-loading rates of individual molecular clutches and correctly predicts cell-adhesion behaviour for a range of substrate stiffnesses. The framework presented can be extended to study complex phenomena such as focal-adhesion maturation and cell-type-specific mechanosensing.

Main

The ability of cells to detect and respond to various mechanical signals, such as an external force¹, substrate stiffness and topography², is crucial for the regulation of many physiological processes, including cell migration, proliferation, differentiation and apoptosis³. Aberrant cell mechanosensing has been implicated in a number of pathological conditions, such as fibrosis, cancer and cardiovascular diseases⁴. Therefore, a better understanding of cell mechanosensing mechanisms is essential for elucidating both physiological and pathological processes.

Molecular linkages between the cell cytoskeleton and the extracellular matrix (ECM), often referred to as molecular clutches, are the primary sites where cells physically interact with their microenvironment and probe its mechanical properties⁵ (Fig. 1a). Molecular clutches experience mechanical tension from both external mechanical cues and intracellular molecular motors. Molecular-clutch theory, which proposes that the tension-dependent formation and dissociation of molecular clutches are integrated at the mesoscale level to guide cell-adhesion behaviour, has become the leading model for understanding cellular mechanosensing processes^{6,7,8,9,10,11,12,13,14,15,16,17,18}. This theory has successfully explained many aspects of cell spreading, migration and traction force generation on substrates with different mechanical properties^{6,7,11,12,13,14,16,17,18}.

Fig. 1: Model set-up.

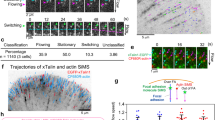
a, Integrins and adaptor proteins such as talin are the main components of cell-adhesion linkages that form between the actin cytoskeleton and the substrate. The myosin II-generated retrograde flow of actin filaments leads to mechanical stretching of these links, causing local substrate deformations (shown in red). Force-transmitting units, each including an intracellular part (integrin and adaptor proteins) and an extracellular part (locally deformed substrate), are referred to in this study as ‘molecular clutches’. b, In the model, molecular clutches are represented by composite springs consisting of two parts: an intracellular one (k_c) and an extracellular one (${k}_{{\rm{s}}}^{{\prime} }$). Although we assume the latter has a linear response to the applied load, we consider the former to be a linear spring in the linear clutch model and a nonlinear spring with a talin-like force response in the talin clutch model. The pulling force (F_m) generated by myosin II motors causes actin filaments to move at a speed v. This leads to a gradual stretching of molecular clutches along the x axis parallel to the substrate surface (contact angle θ ≈ 15°)⁶⁵, resulting in their extension, l. This, in turn, allows transmission of the myosin II-generated force (F_m) to the substrate, leading to the cell traction force (F_c), which causes deformation of the substrate (x_s) over the entire area of cell-adhesion complexes. The efficiency of the force transmission is mainly determined by the kinetic behaviour of molecular clutches under a mechanical load, which is described by their formation and dissociation rates, k_on and k_off, respectively. The viscoelastic behaviour of the substrate at the scale of cell-adhesion complexes is described in the study using the Kelvin–Voigt model, which represents substrate deformations as a purely elastic spring with stiffness k_s, connected in parallel to a purely viscous damper characterized by viscosity constant ξ_s. In general, by replacing the Kelvin–Voigt model with the Maxwell model or the standard linear solid model, it is possible to describe the mechanosensitive behaviour of cell-adhesion complexes on liquid-like materials and on materials with more complex viscoelastic behaviour, respectively. SLS model, standard linear solid model.

Despite this, recent experimental studies using FRET tension sensor tools have revealed substantial discrepancies between measured force-loading rates of molecular clutches and those predicted by conventional molecular-clutch models, highlighting the need to revise the conceptual framework. For example, tension-gauge DNA sensors show that molecular clutches experience force-loading rates of 0.2–4 pN s⁻¹ in living cells grown on rigid substrates^19,20, which is several orders of magnitude lower than the 60–8,000 pN s⁻¹ predicted by existing molecular-clutch models^{7,11,12,13,14} (Extended Data Table 1). Moreover, these experiments show that the force-induced binding of vinculin to talin considerably reduces the force-loading rate and prolongs the lifetime of molecular clutches, even when the actin-binding ability of vinculin is compromised²⁰, challenging the widely accepted notion that the primary function of vinculin is to enhance focal adhesion (FA) by recruiting more actin filaments^13,21.

An important aspect often overlooked in existing molecular-clutch models is the elastic properties of intracellular molecular-clutch components, which are typically approximated by linear springs with stiffness ranges of ~1–1,000 pN nm⁻¹ (refs. ^{7,11,12,13,14}). However, single-molecule measurements have shown that key adaptor proteins in molecular clutches, such as talin, are orders of magnitude more elastic due to the presence of long flexible peptide linkers and force-induced unfolding of protein domains, which are capable of extending beyond 200 nm under only a few piconewtons of force^22,23. The nonlinear force response and high elasticity of talin effectively act as a ‘shock absorber’ that radically alters force transmission across cell-adhesion complexes^22,23, potentially explaining the lower force-loading rates and longer lifetimes of molecular clutches observed in experiments^19,20. Yet, it remains unclear how this behaviour affects cellular mechanosensitivity.

To address these gaps, we developed a semi-analytical model that integrates the experimentally measured force response of adaptor proteins together with local substrate deformations at the attachment sites of molecular clutches. By incorporating the nonlinear elasticity of adaptor proteins such as talin, the model was able to capture key experimental observations, including force-loading rates and the dynamics of molecular clutches. We found that molecular clutches act as a ‘differential’ that allows the actin cytoskeleton and substrate to have different movement rates while maintaining a stable mechanical connection between them. This framework reconciles discrepancies between previous molecular-clutch models and experimental observations and provides a basis for further study of the FA maturation process and cell-type-specific mechanosensing.

Results

Semi-analytical mechanical model of cell-adhesion complexes

To study the potential effect of the elastic properties of molecular clutches on the mechanosensing behaviour of cell adhesion, we developed a semi-analytical theoretical framework consistent with the experimentally observed force response of molecular-clutch components at the single-molecule level^22,24,25 and experimentally measured tension^26,27 and force-loading rates of molecular clutches^19,20. This allowed a comprehensive study of the dynamic aspects of cell-adhesion mechanics, which provided new insights into the role of different cellular elements in shaping mechanosensitive cell-adhesion behaviour.

Notably, our model can be used to describe two types of cell-adhesion complexes: talin-based and non-talin-based. In the former case, cell-adhesion complexes correspond to individual nascent adhesions (NAs) and FAs, whereas in the latter case, they represent sets of integrin clusters observed in experiments on talin-deficient cells¹³.

In the model, large-scale substrate deformations at the scale of cell-adhesion complexes are described using the Kelvin–Voigt model (Fig. 1b), which depicts the behaviour of elastic-like substrates with residual viscosity commonly used in experiments, such as acrylamide hydrogel and polydimethylsiloxane^28,29. However, in principle, our model also allows for the incorporation of any other physical model describing substrate deformations, including the Maxwell model for liquid-like substrates (Fig. 1b) or even the more general standard linear solid model.

Furthermore, individual molecular clutches are represented in our model by two-part springs: one part describes cell adaptor proteins connecting adhesion receptors to the cytoskeleton, and the other part depicts local deformations of the substrate at the attachment sites of the adhesion receptors (Methods and Fig. 1). The elasticity of adaptor proteins is approximated either by linear springs or by a more realistic nonlinear force response described by the worm-like chain model (Methods and Supplementary Appendix F), which better reflects the experimentally observed force-induced softening of adaptor proteins, such as talin, caused by the unfolding of mechanosensitive protein domains. The local substrate deformations are related to the substrate rigidity through a spring constant, the value of which can be obtained from the theory of elasticity (equation (1) and Supplementary Appendix A).

The model distinguishes between the ‘occupied’ (‘on’) and ‘free’ (‘off’) states of sites available for the formation of molecular clutches. It quantifies the deformation of each molecular clutch under the influence of a mechanical load created by the contractile activity of myosin II motors. The dynamic behaviour of cell-adhesion complexes in the model is determined by the balance between the force generated by myosin II motors, which pulls on actin filaments within adhesion complexes, and the traction force created by mechanically stretched molecular clutches in accordance with Newton’s third law. When this balance is disturbed (due to the formation or dissociation of molecular clutches), it is restored due to the convergence of the molecular-clutch system to a stable stationary state corresponding to a steady state of the system (Extended Data Fig. 1). Thus, stable stationary states provide information about the long-term behaviour of the molecular-clutch system. By finding the probability distribution for the extension of molecular clutches in stationary states for a given substrate rigidity and knowing how the tension of molecular clutches depends on their extension, one can then calculate the total traction force created by a cell-adhesion complex resulting from the molecular-clutch-mediated transmission of the pulling force generated by myosin II motors (Fig. 1b and equation (6)). The efficiency of this force transmission, which is determined by the dynamics of molecular-clutch formation and dissociation, is a key element for understanding the mechanosensitive behaviour of cell adhesion, as can be seen from the master equation describing the time evolution of the molecular-clutch system (Supplementary equation (B10)).

A key feature of our model, revealed by exploring the model parameter space, is that it can predict diverse dynamic behaviours of cell-adhesion complexes, which are jointly determined by a number of sensitive model parameters, including the rate of molecular-clutch formation, adaptor-protein elasticity and myosin II density. As shown in Fig. 2a, three characteristic types of cell-adhesion behaviour were observed on varying the rate of molecular-clutch formation and adaptor-protein elasticity. The first was the strong cell-adhesion regime, in which cell traction increases monotonically with the substrate rigidity (Fig. 2a). This monophasic behaviour is consistent with the behaviour of wild-type (WT) fibroblast cells observed in experiments¹³. This regime corresponds to a high rate of molecular-clutch formation and high adaptor-protein elasticity, which buffer the tension experienced by individual molecular clutches and keep it at a low level, so that a sufficiently large number of molecular clutches can be formed to maintain strong cell traction. By contrast, when the rate of molecular-clutch formation is low and the adaptor proteins are stiff, cell traction exhibits a biphasic behaviour, increasing on soft substrates and decreasing on stiffer ones due to the shorter lifetime of molecular clutches because of their higher tension (Fig. 2a), reminiscent of the behaviour of talin-knockout (KO) fibroblasts¹³. Interestingly, for a certain range of adaptor-protein stiffnesses and molecular-clutch formation rates, the model predicts a bistable region in which both strong and weak cell-adhesion regimes coexist on rigid substrates. The molecular-clutch system in this case resembles the clutch of a car, where the state of strong cell adhesion corresponds to a low gear and the state of weak cell adhesion to a high gear. The bistability mode is essentially a state with a ‘rev matching’ condition that allows cells to ‘switch gear’ and change between states with strong and weak adhesion.

Fig. 2: Adaptor-protein elasticity separates molecular clutches into different groups.

a, Stability diagram of cell-adhesion complexes. Solid curves (black, red and blue) show bifurcations that lead to the formation of a bistability region (red area) and a biphase–monophase boundary (green dotted curve), which affect the mechanosensitive behaviour of cell adhesion (‘Steady-state behaviour and bifurcation of the clutch system’). The insets around the bistability region illustrate representative cell traction curves within each domain. It is evident that increasing the stiffness of the intracellular part of molecular clutches (k_c) changes the shape of the cell traction curve, shifting cells from the soft-clutch behaviour of MEF WT cells to the rigid-clutch behaviour of MEF Talin 1 KO, Talin 2 shRNA cells. b, Ensemble-averaged force–extension curves of nonlinear talin-based molecular clutches (talin WT model) for different values of Young’s modulus for the substrate (E). Dashed lines represent the force–extension curves of molecular clutches with folded and unfolded mechanosensitive R3 domains of talin at the corresponding value of Young’s modulus for the substrate. Inset: close-up of curves for 10 kPa. c,d, Fitting of experimental data for cell traction (c) and retrograde actin flow (d) from refs. ^13,21 collected for MEF WT cells (red circles) and MEF Talin 1 KO, Talin 2 shRNA cells (green triangles) to the linear clutch model (linear WT and linear KD model, solid curves) and to the nonlinear talin clutch model (talin WT model, dotted curves), respectively. Both WT models reproduce the WT data, indicating that talin can be approximated as a linear spring for the substrate elasticities used in the experiment. The fitted parameter values of the linear models (Extended Data Table 2) reveal two molecular-clutch archetypes: a soft, talin-dominant one, prevalent in WT cells, and a more rigid, talin-depleted one, prevalent in talin-deficient cells.

In addition to the rate of molecular-clutch formation and adaptor-protein elasticity, these three types of cell-adhesion behaviour also depend on the densities of myosin II motors and ECM ligands, which will be discussed in more detail in the following sections. Because most of these parameters can be modulated by cells through regulating cell contractility and the composition of FAs, cells can potentially switch between the weak and strong adhesion states.

Effect of elasticity of adaptor proteins on cell adhesion

Using a few physiologically relevant fitting parameters (Extended Data Table 2), we found that our model could fit well previously published experimental data, such as retrograde actin flow and cell traction measured at different values of Young’s modulus for the substrate^13,21,30 (Fig. 2c,d). This makes it possible for the model to be used to plot cell-adhesion stability diagrams and extract detailed information about molecular-clutch dynamics at the single-molecule level from experimental data obtained from cells, including the average tension and conformational changes of molecular clutches, which may provide new insights into the key factors regulating FA behaviour.

Previous single-molecule experiments showed that the mechanical responses of adaptor proteins, such as talin, are highly nonlinear and subject to force-induced softening due to the unfolding of their force-bearing protein domains. Therefore, we first investigated how the nonlinear elasticity of adaptor proteins affects the mechanosensitivity of cell adhesion. To do this, we treated the intracellular part of molecular clutches as a nonlinear spring with a force response corresponding to that of talin measured in single-molecule studies²², including the force-dependent unfolding of the mechanosensitive R3 domain of talin. See the talin WT model described in Supplementary Appendix F.

Fitting experimental data about the mechanosensitive behaviour of mouse embryonic fibroblast (MEF) WT cells from ref. ¹³ to the steady-state solution of the talin WT model (Fig. 2c,d) using the model-fitting parameters listed in Extended Data Table 2 revealed that even at the highest substrate stiffness, most talin-based molecular clutches experienced relatively low tension in the range 0.7–1.3 pN (Supplementary Fig. 1b). This tension was below the force level at which the nonlinear elastic properties of talin become strongly pronounced (Fig. 2b). In addition, the model predicted that on rigid substrates, only a small percentage (1–2%) of talin-based molecular clutches would be subject to forces sufficient to substantially stretch talin molecules and trigger the unfolding of their mechanosensitive domain (Supplementary Fig. 1a). This finding is in good agreement with a recent experimental study performed on Xenopus laevis cells grown on a fibronectin-coated glass substrate, in which only about ~4% of talin molecules underwent substantial conformational changes upon stretching the molecular clutch³¹.

These results indicate that if the elasticity of adaptor proteins has any effect on cell traction and retrograde actin flow, it is the passive linear elasticity of adaptor proteins that is important. Accordingly, the experimental data from ref. ¹³ could be fitted to a simplified model in which the intracellular part of molecular clutches is represented by a linear spring (the linear WT model) as accurately as the talin WT model with a more realistic nonlinear force response of the intracellular part of molecular clutches (Fig. 2c,d).

Further comparison of model parameter values obtained by fitting experimental data collected from WT and talin-depleted MEF cells to the linear molecular-clutch model confirmed that the elasticity of adaptor proteins is, indeed, one of the key factors influencing cell-adhesion behaviour. For MEF WT cells, the fitted elasticity of the intracellular parts of molecular clutches (k_c = 0.05 pN nm⁻¹) was found to be close to the elasticity of talin estimated from previous single-molecule measurements (0.09 pN nm⁻¹; Supplementary Table 3). On the other hand, the intracellular parts of molecular clutches in MEF Talin 1 KO, Talin 2 shRNA cells were predicted to be more than ten times stiffer (k_c = 1.6 pN nm⁻¹) compared to MEF WT cells. Because previous single-molecule studies have shown that typical cytoskeletal proteins found in cell-adhesion complexes have elasticities less than 0.3 pN nm⁻¹ (Supplementary Table 3), these data indicate that rigid molecular clutches may form through the clustering of adaptor proteins. Indeed, FA proteins such as kindlin and α-actinin have been shown to bind to FAs before talin and form clusters or condensates^32,33,34. Because these proteins are also present in MEF Talin 1 KO, Talin 2 shRNA cells, they could potentially contribute to the increase in molecular-clutch rigidity predicted by the model. This result is supported by the much larger characteristic size of the adhesion site of molecular clutches in talin-KO cells (r = 26 nm) compared to WT cells (r = 0.6–0.8 nm), which was obtained by fitting experimental data (Extended Data Table 2). In the future, super-resolution microscopy could be used to test the model-predicted difference between the characteristic sizes of adhesion sites of talin-based and non-talin-based molecular clutches. Overall, our model indicates that there are two types of molecular clutches in MEF cells—soft, talin-based and rigid, non-talin-based—which are formed by clustered adaptor proteins. Indeed, a model describing the competitive formation of these two types of molecular clutches (WT-2 model; Supplementary Appendix G) was found to more closely fit the experimental data obtained from WT and talin-depleted MEF cells (Extended Data Fig. 2a,b).

Finally, a more detailed analysis of the force–extension curves of nonlinear talin-based molecular clutches at different values of Young’s modulus for the substrate (E) showed that on soft substrates (E ≤ 10 kPa), the mechanosensitive behaviour of cell adhesion is determined primarily by the elastic characteristics of the extracellular part of the molecular clutches (local substrate deformations), whereas on rigid substrates (E > 10 kPa), the elasticity of the intracellular part of the molecular clutches begins to play a more important role in this process (Fig. 2b). This result is in good agreement with the graphs presented in Extended Data Fig. 3a,b, which show that the spring constant of the intracellular part of molecular clutches (k_c) affects cell behaviour only on rigid substrates, but not as much on soft ones. Thus, the elasticity of both the intracellular and extracellular parts of molecular clutches is a key factor influencing the mechanosensitive cell-adhesion behaviour on substrates with different stiffnesses. Because many adaptor proteins contain long stretches of conserved intrinsically disordered regions, such as tensin, these results imply that such flexible domains may play an important role in regulating the mechanosensitive behaviour of cell adhesion.

Ligand density affects cell adhesion through myosin II feedback

To investigate the effect of the density of molecular clutches on cell adhesion, we fitted previously published experimental data on MEF WT cells and MEF Talin 1 KO, Talin 2 shRNA cells plated on elastic substrates that were coated with different fibronectin concentrations¹³. Because the density of the fibronectin network affects the rate of molecular-clutch formation and the distribution of the mechanical load near adhesion sites of molecular clutches, the data were fitted by varying the clutch formation rate and the characteristic size of adhesion sites of molecular clutches. The density of myosin II motors was also varied. Using this approach, the experimental data could be fitted fairly well to the linear knockdown (KD), linear WT and talin WT models (Fig. 3a,b).

Fig. 3: Ligand density influences molecular-clutch kinetics and myosin II organization.

a,b, Cell traction measured on MEF WT cells (a) and MEF WT and MEF Talin 1 KO, Talin 2 shRNA cells (b) plated on substrates coated with increasing concentrations of fibronectin¹³. The experimental data were fitted to the talin WT model (dotted curves) and the linear WT and KD models (solid curves) by varying the rate of molecular-clutch formation (${k}_{{\rm{on}}}^{0}$), the characteristic size of adhesion sites of molecular clutches (r) and the density of myosin II motors (σ_m). Other model parameters were held fixed (Supplementary Table 1). c, The best-fitting parameter values as a function of fibronectin density show that enriching the ligand density accelerates molecular-clutch formation, reduces the characteristic size of adhesion sites of molecular clutches and increases the density of myosin II, thereby enhancing actin–substrate force transmission. d, Structured illumination microscopy image of an NIH-3T3 fibroblast expressing myosin RLC-GFP. Inset: close-up of the boxed region. e,f, Quantification of myosin II filament stacks in NIH-3T3 and HeLa cells. Increasing the fibronectin density did not alter the density of myosin II stacks (e) but did alter their projected area in a cell-type-dependent manner (f). The response of NIH-3T3 cells is consistent with model predictions for MEF WT cells. In e from left to right, N = 13, 11, 14, 13, 12 and 16 cells were processed under the corresponding experimental conditions. In f from left to right, N = 2,534, 846, 3,836, 834, 2,305 and 928 stacks of myosin II filaments were collected and processed under the corresponding experimental conditions from the same number of cells as indicated for e. Boxes and error bars in e represent mean ± standard errors of the mean (s.e.m.) and standard deviation, respectively. The circles in f show the median, and boxes represent the mean ± s.e.m. The pairwise statistical difference between the corresponding datasets was calculated using one-way ANOVA with post-hoc Tukey’s honestly significant difference test (no adjustments).

Interestingly, the fitted data showed a correlation between myosin II motor density (σ_m) and fibronectin concentration, as the fitting did not converge when the myosin II density was fixed. According to the model, the density of myosin II motors pulling on actin filaments decreased by ~25% on substrates coated with 1 μg ml⁻¹ fibronectin solution compared to those coated with 100 μg ml⁻¹ fibronectin solution (Fig. 3c). To test this model prediction, we transfected NIH-3T3 cells with the myosin regulatory light chain (RLC)-GFP³⁵ and measured the density and the average size of stacks of myosin II filaments labelled with this construct as a function of the fibronectin concentration (Fig. 3d–f). As a control, we also performed similar measurements with HeLa cells.

We found that, although in HeLa cells myosin II motors formed more or less uniform assemblies resembling beads on a string (Supplementary Fig. 2), in NIH-3T3 cells, they formed stacks that were more irregularly shaped (Fig. 3d). More importantly, although the fibronectin concentration was found to have little effect on the density of stacks of myosin II filaments in both NIH-3T3 and HeLa cells (Fig. 3e), it had a strong effect on their average size in NIH-3T3 cells (~35% drop for a 1 μg ml⁻¹ fibronectin solution compared to a 100 μg ml⁻¹ solution) but not in HeLa cells (Fig. 3f), indicating that this effect may depend on cell type. Thus, the model developed in our study can accurately capture the mechanical states of fibroblast cells and make physiologically relevant predictions.

Previous studies have shown that fibronectin density can influence the activation of rho kinase (ROCK) in endothelial cells. ROCK controls the assembly of myosin II filaments³⁶. Thus, MEF cells could potentially use a similar mechanism. However, the precise molecular pathways responsible for the fibronectin-dependent activation of ROCK remain unknown. Because our observations indicate that such a feedback loop depends on cell type, it may be possible to gain detailed insights into the origin of this phenomenon by comparing normal and transformed cells.

Vinculin modulates force-loading of molecular clutches

Having established that the model can reproduce the mechanosensitive behaviour of cell adhesion, such as traction force and retrograde actin flow, we next tested whether the model can describe the mechanical dynamics of individual molecular clutches. Recent advances in the development of tension-gauge DNA sensors have made it possible to directly measure the force-loading rate and lifetime of integrin–ECM adhesion bonds. Experimental studies have shown that individual molecular clutches can experience forces above 40 pN, whereas measured force-loading rates are in the range 0.2–4 pN s⁻¹ (refs. ^19,20). Furthermore, the force-loading rate seems to vary with the molecular-clutch tension²⁰. For example, it takes much longer for molecular clutches to reach a tension of 7–19 pN than to subsequently achieve a tension of 19–41 pN, a phenomenon that cannot be explained by existing models in which molecular clutches are represented by linear springs, because the force-loading rate of such molecular clutches does not depend on the applied tension. In addition, Hu et al. demonstrated that vinculin plays an important role in stabilizing the tension experienced by molecular clutches, as MEF vinculin-KO cells showed an increased force-loading rate and reduced lifetime of adhesion bonds²⁰. The latter result is counter-intuitive, as the measured maximum tension experienced by molecular clutches in MEF vinculin-KO cells was lower than that in MEF WT cells, which is in good agreement with the experimentally observed reduction in cell traction in MEF vinculin-KO cells²¹. Because the binding of vinculin to talin, on the one hand, stabilizes molecular clutches^37,38 and, on the other hand, keeps talin in an unfolded state²² causing an increase in the elasticity of molecular clutches, we tested whether these two factors are the main ones responsible for the observed effect of vinculin on cell traction and force-loading rates of molecular clutches.

To do this, we first tested the effect of vinculin KO by fitting cell traction and retrograde actin flow measured in MEF vinculin-KO cells²¹ to the WT-2 model. For this purpose, we used the dissociation rate of talin-based molecular clutches as a model-fitting parameter, because molecular clutches in MEF vinculin-KO cells are expected to be less stable due to the loss of vinculin–actin interactions that stabilize talin association with the actin cytoskeleton^39,40,41. As shown in Fig. 4c,d, the WT-2 model correctly predicted a decrease in cell traction and an increase in retrograde actin flow compared to MEF WT cells in this case (blue curve). The fitted dissociation rate of molecular clutches showed a 30% increase compared to MEF WT cells, consistent with vinculin having a role in stabilizing molecular clutches. The fitting further improved when we added the myosin II density (σ_m) as another model-fitting parameter to phenomenologically account for the loss of tension transferred by vinculin molecules to talin (Fig. 4c,d, magenta curve). In this case, the model predicted a 60% increase in the dissociation rate of molecular clutches and a 20% decrease in the number of myosin II molecules exerting a mechanical load on molecular clutches. The decrease in myosin II density compensates for the increases in retrograde actin flow caused by the increase in the dissociation rate of molecular clutches and at the same time reduces cell traction, thus providing a better fit to the experimental data obtained in MEF vinculin-KO cells. Thus, the fitting results indicate that vinculin influences both the mechanical load of molecular clutches and their stability, which is in good agreement with published experimental data²¹.

Fig. 4: Vinculin recruitment modulates molecular-clutch stability and force-loading rate.

a, Numerical solution of the master equation describing NA maturation (Supplementary equation (I1)). The calculations show that the occupancy probability of sites available for molecular-clutch formation by molecular clutches with folded talin (blue curve) reaches a steady-state level within 10–20 s, whereas the amount of vinculin-bound molecular clutches (green curve) grows more slowly due to the limited pool of molecular clutches with force-unfolded talin (red curve). b, Total internal reflection fluorescence measurements of NA area (blue) and also talin (yellow) and vinculin (green) intensities in NAs in NIH-3T3 cells (mean ± s.e.m., N = 437 peripheral NAs pooled from four cells), fitted to the talin WT model. Talin accumulates first, because for vinculin to bind to it requires the unfolding of the mechanosensitive R3 domain of talin. c,d, Retrograde actin flow (d) and cell traction (c) data for WT (red circles), vinculin-KO (green triangles) and vinculin VD1-expressing MEF cells (blue triangles)^13,21 fitted to the WT-2 model, which accounts for vinculin-dependent changes in the dissociation rate and tension of molecular clutches. The fit shows that vinculin enhances the stability and mechanical load of molecular clutches. e, Force-loading rates of molecular clutches predicted by the model at their different tensions in mature FAs. Higher force-loading rates were predicted for molecular clutches under higher tension. f, Force-loading rates of molecular clutches in the presence of different vinculin mutants predicted by the talin WT model. KO of vinculin (blue) or vinculin with reduced talin binding affinity (vinA50I, red) markedly accelerates the force-loading rate of molecular clutches and increases the sensitivity to the density of sites available for molecular-clutch formation, whereas vinculin with reduced actin-binding affinity (vinI997A, yellow) has little effect compared to MEF WT cells (green). Experimental data were digitalized from ref. ²⁰ (mean ± 95% confidence interval for three independent experiments). g, Force–extension curves of talin alone (no VD1) and in the presence of vinculin VD1 (cycles 1–3)²². Binding of vinculin VD1 to force-unfolded talin domains prevents their refolding, increasing talin extension in the 5–10 pN range by almost threefold, thereby softening talin. Vcl, vinculin. Panel g adapted from ref. ²² under a Creative Commons license CC BY 4.0.

We then calculated the dynamics of the talin-based molecular-clutch system in the presence of vinculin–talin interactions. To do this, we added three kinetic rates to the talin WT model, shown in Supplementary Table 4. These rates describe the kinetics of vinculin association or dissociation from the unfolded mechanosensitive R3 domain of talin (${k}_{{\rm{on}}}^{{\rm{R3v}}}$ and ${k}_{{\rm{off}}}^{{\rm{R3v}}}$, respectively) and the formation of molecular clutches by vinculin-bound talins (${k}_{{\rm{on,v}}}^{0}$; Supplementary Appendix I). The values for the first two rates were taken from previously published single-molecule experimental measurements²⁵. The value of the ${k}_{{\rm{on,v}}}^{0}$ rate was chosen based on the assumption that vinculin-bound talins remain inside FAs even after the dissociation of molecular clutches from the substrate, so that they can readily form new molecular clutches compared to vinculin-unbound talins. Furthermore, based on previously published experimental data²², it was assumed that by binding to mechanically unfolded talin, vinculin locks it in the unfolded, more elastic state until it dissociates from talin. Finally, the effect of vinculin-mediated stabilization of talin-based molecular clutches was modelled by increasing the dissociation rate of such molecular clutches when vinculin is not bound to them to a value found by fitting the cell traction and retrograde actin flow data shown in Fig. 4c,d.

As shown in Fig. 4a,b, the evolution of the molecular-clutch system predicted by the model in this case has dynamics like those in the formation of NAs, as the kinetics of talin and vinculin accumulation within NAs and changes in NA area are like those observed in experiments performed on NIH-3T3 cells. The total amount of talin in NAs was found to increase rapidly, reaching within seconds ~50% of the total change in integral talin intensity in NAs observed during the first 3 min, whereas vinculin recruitment due to the binding to talin had a slower trend. Further calculations showed that the average force-loading rate of molecular clutches at various tension values in the range 0–30 pN also agrees well with experimental observations that demonstrate a highly nonlinear change in the force-loading rate with the tension experienced by molecular clutches²⁰ (Fig. 4e). Furthermore, the average force-loading rate of molecular clutches is in the range 0.2–5 pN s⁻¹, which is in good agreement with the experimental results obtained using tension-gauge DNA sensors^19,20.

We then tested the effects of vinculin-KO and vinculin A50I and I997A mutants with reduced binding affinity to talin and actin, respectively, on the force-loading rate of molecular clutches. To do this, vinculin-KO/A50I was treated in the model by setting ${k}_{{\rm{on}}}^{{\rm{R3v}}}=0$ (no vinculin binding to talin). Additionally, the model parameter α, which describes the average number of new sites available for molecular clutch formation that are added to NAs and FAs upon unfolding of the mechanosensitive R3 domain of talin and subsequent binding of vinculin to it, was set to zero: α = 0 (no vinculin-mediated force-induced enhancement of NAs and FAs). As for the vinculin I997A mutant, the same ${k}_{{\rm{on}}}^{{\rm{R3v}}}$ and α values were used as in the case of MEF WT cells, but ${k}_{{\rm{on,v}}}^{0}$ was set to zero: ${k}_{{\rm{on,v}}}^{0}=0$ (as there is no rebinding of vinculin-associated molecular clutches after their dissociation from the substrate, because the vinculin I997A mutant is potentially unable to retain talin in NAs and FAs due to its reduced binding affinity for actin). In addition, for both vinculin-KO/A50I and vinculin I997A, the dissociation rate of molecular clutches was set to a higher level and the myosin II density was set to a lower level in the model calculations compared to MEF WT cells, according to the results shown in Fig. 4c,d. We calculated the effects of these mutants on the molecular-clutch dynamics on a rigid substrate coated with different ligand densities. The results showed that vinculin-KO and vinculin mutants strongly affected the force-loading dynamics of molecular clutches (Fig. 4f). In good agreement with experimental observations²⁰, an increase in the average force-loading rate was observed for the vinculin-KO/A50I mutant, whereas the vinculin I997A mutant resulted in a negligible change in the force-loading rate (Fig. 4f). Furthermore, our model also correctly predicted the dependence of the force-loading rate of molecular clutches on the substrate ligand density, as there was an increase in the force-loading rate at lower ligand densities in all experimental conditions, with the most pronounced effect observed under vinculin KO conditions (Fig. 4f).

Overall, these results indicate that the mechanical stability of molecular clutches and the nonlinear force response of talin regulated by vinculin binding strongly affect the dynamics of molecular clutches. On the one hand, vinculin depletion reduces the stability of molecular clutches, leading to a decrease in cell traction under vinculin KO conditions. On the other hand, the binding of vinculin to the mechanosensitive R3 domain of talin and the locking of the latter in the unfolded state leads to an overall softening of talin, reducing the build-up of talin tension. In addition, due to the nonlinear force response of talin, which exhibits higher elasticity at lower stretching forces, the tension build-up in talin will be slower in the lower force range compared to the higher force range, in good agreement with experimental observations (Fig. 4e,g).

To illustrate the contribution of talin elasticity to the force-loading dynamics of molecular clutches, we produced qualitative estimates based on single-molecule measurements of the force response of talin in the absence and presence of vinculin binding²². As shown in Fig. 4g, the measured end-to-end extension of the folded talin under a tension of 10 pN is ~40 nm greater than that under a tension of 5 pN. For talin with all nine domains containing unfolded vinculin binding sites, the difference in the end-to-end extension of talin at the same tension values is ~110 nm. Considering the retrograde actin flow of ~7–10 nm s⁻¹ obtained from fitting experimental data to the talin WT model with rigid substrates (E ≥ 1 MPa; Fig. 2d), we easily found the values of the force-loading rate in both cases to be ~0.9–1.3 and ~0.3–0.5 pN s⁻¹ in the absence and presence of vinculin binding to talin, respectively, which are in good agreement with experimental measurements²⁰ (Fig. 4f, experiment). This effect of vinculin on talin stiffness and force-loading rates of molecular clutches is mediated solely by vinculin binding to talin and does not require vinculin to bind to actin. Accordingly, our model predicts that the force-loading rates of molecular clutches in MEF WT cells and MEF vinculin I997A cells should be very similar, which is also in good agreement with experimental data (Fig. 4f).

Finally, using the same parameter values fitted for MEF WT cells, our model was also able to reproduce experimental observations of the mechanosensitive cell-adhesion behaviour on liquid-like viscoelastic substrates, which in the simplest case can be described by the Maxwell model, thus highlighting the robustness of our model predictions (Extended Data Fig. 4).

Steady-state behaviour and bifurcation of the clutch system

To further investigate the dynamic behaviour and stability of cell-adhesion complexes under different physiological conditions, we used the linear KD and linear WT models, which were found to accurately fit cell traction and retrograde actin flow measurements made in cells plated on substrates of different elasticities.

First, we mapped the bistability region in the space of model parameters. To do this, we varied the values of the spring constant of the intracellular part of molecular clutches (k_c) and the myosin II density (σ_m) in the linear KD and linear WT models (Fig. 5). As a result, for the MEF Talin 1 KO, Talin 2 shRNA cells, the bistability region was found to be localized at moderate values of the myosin II density, close to the parameter range of the linear KD model corresponding to MEF Talin 1 KO, Talin 2 shRNA cells (Fig. 5a,e). This finding indicates that molecular clutches probably experience the bistability in myosin II-depleted regions of such cells that can often be found at the cell periphery⁴². Indeed, experiments have recently shown that filopodia exhibit both strong and weak adhesion to fibronectin-coated substrates in a myosin II-dependent manner⁴².

Fig. 5: Bistability of cell adhesion.

a,b, Stability diagrams of the linear KD (a) and linear WT (b) models. Three-dimensional red shapes and triangles denote the bistability regions and their projections, respectively. Yellow cylinders represent the model parameter ranges corresponding to MEF Talin 1 KO, Talin 2 shRNA and MEF WT cells. The blue dotted contour in a indicates a cross section of the bistability region detailed in c. Notably, talin-deficient MEF cells lie close to this region, whereas MEF WT cells are far from it, indicating that the high elasticity of talin stabilizes NAs and FAs. c, Close-up of a cross section of the bistability region indicated in a. Its boundaries are formed by the trajectories of the two saddle-node points shown in d. The bistability region arises from a cusp-type catastrophe when the rigidity of the intracellular part of molecular clutches is sufficiently large. d, Cusp catastrophe experienced by the molecular-clutch system. The pale green surface depicts cell traction (P) as a function of the retrograde actin flow (v) and substrate elasticity (E) in the linear KD model. The solid and dashed curves denote the stable and unstable branches of the solution for different myosin II densities (σ_m). Reducing σ_m to ~44 μm⁻² results in the appearance of two saddle-node bifurcation points, a typical sign of a cusp catastrophe. Further decreasing σ_m shifts these points along the surface, outlining an instability region that includes only the unstable branches of cell traction curves. e,f, Stability diagrams of cell adhesion complexes in the case of MEF Talin 1 KO, Talin 2 shRNA cells (e) and MEF WT cells (f) obtained by projecting the bistability regions shown in a and b onto the horizontal plane. The black, red and blue solid curves mark the onset of the cusp catastrophe and bifurcations due to saddle-node points moving to infinity, which lead to the formation of biphase–monophase boundaries (green dotted curves), which affect the shapes of cell traction curves both within and beyond the bistability region. The insets around the bistability region illustrate representative cell traction curves within each domain. The graphs show that the elasticity of the intracellular part of molecular clutches and the myosin II density have a profound effect on the mechanosensitive behaviour of cell adhesion.

In addition, we fitted previously published experimental data collected for MEF Talin 1 KO, Talin 2 shRNA cells treated with a myosin II inhibitor, blebbistatin¹³, to the linear KD model. We found that these cells begin to develop bistable cell-adhesion behaviour when the density of myosin II motors in them decreases by ≳1.6 times (15 μM blebbistatin case; Extended Data Fig. 5a), with a further decrease in the myosin II density leading to a more pronounced bistability of cell adhesion (50 μM blebbistatin case; Extended Data Fig. 5a). On the other hand, blebbistatin-treated MEF WT cells did not seem to exhibit bistable cell-adhesion behaviour (Extended Data Fig. 5b), mainly due to the very high elasticity of talin-based molecular clutches, which results in MEF WT cells being far from the corresponding bistability region in the model parameter space (Fig. 5b,f). This finding indicates that talin molecules could potentially play an important role in stabilizing NAs and FAs during their maturation.

The existence of stable stationary states at each value of Young’s modulus for the substrate indicates that the molecular-clutch system should converge over time to one of these states, which, thus, represent possible steady states of the system. To find out how quickly the molecular-clutch system reaches these stationary states starting from an initial configuration with zero adhesion bonds between a cell and the substrate, we used the finite-difference method to numerically solve the master equation describing the time evolution of the molecular-clutch system (Supplementary equation (B10)). Both the linear WT and linear KD models predicted the rapid convergence of key experimental observables, such as cell traction and retrograde actin flow, to their stationary values within ~10–20 s (Extended Data Figs. 6a,b and 7a,b). The probability distribution of molecular-clutch extension also demonstrated rapid convergence to the steady-state distribution given by equation (9) in as little as 20 s (Extended Data Figs. 6c and 7c). These results are in good agreement with previous experimental observations showing that the retrograde flow of actin filaments in filopodia or near the edges of living cells occurs at an almost constant rate (v(t) ≈ const.)^{7,13,21,42,43}, indicating that cell-adhesion complexes should function close to a steady state.

Furthermore, the characteristic relaxation time of the molecular-clutch system to the steady state predicted by our model for elastic-like substrates was two to four orders of magnitude less than the average lifetime of FAs (Extended Data Figs. 6e and 7e and Supplementary Table 5), indicating that they spend more than 98% of their time in a steady or quasi-steady state. In addition, from Supplementary Table 5, it is clear that the experimentally measured characteristic binding and dissociation times of vinculin and paxillin to or from FAs are an order of magnitude greater than the characteristic relaxation time of the molecular-clutch system to a steady state. This result indicates that talin may serve as a rapid response protein that helps establish the initial landscape of molecular clutches in a substrate-mechanosensitive manner, which can subsequently be reinforced and shaped by vinculin or paxillin into matured FAs, in good agreement with previous experimental data^{13,21,26,27,44}.

Discussion

In this work, we developed a semi-analytical model of cell adhesion based on the molecular-clutch theory to examine the potential roles of adaptor-protein elasticity, local substrate deformations, and myosin II and ligand densities on the mechanosensitive behaviour of cell adhesion. One of the main differences between our model and previous studies is that we took a more explicit approach to modelling the elastic properties of adaptor proteins and substrate deformations. Then, by deriving a semi-analytical steady-state solution to the differential master equation of the model, we were able to evaluate experimental observables characterizing the mechanosensitive behaviour of cell-adhesion complexes, such as cell traction force and the rate of retrograde actin flow, using experimentally measured parameters, such as the stiffness of adaptor proteins and the dissociation rate of molecular clutches. This allowed us to identify several important factors that have a major impact on the mechanosensing behaviour of molecular clutches but which are not discussed in detail in the literature.

First, our work highlights the important role of the elastic properties of adaptor proteins, in particular talin, in the mechanosensory behaviour of cells. We showed that the difference in elasticity of talin and other adaptor proteins is one of the key parameters responsible for the different mechanosensitive adhesion behaviour of WT cells and talin-deficient cells. Increasing the stiffness of adaptor proteins, mimicking talin KO and KD conditions, results in decreased molecular-clutch density and reduced cell traction, altering cell behaviour in line with experimental observations¹³.

The inclusion of elastic adaptor proteins results in the molecular-clutch system behaving fundamentally differently from descriptions in previously published studies. Conventional molecular-clutch models assume that molecular clutches have a sufficiently high stiffness (1 pN nm⁻¹ to 1,000 pN nm⁻¹ range^{7,11,12,13,14}), which results in tight coupling between the substrate and the retrograde actin flow, leading to the ‘load-and-fail’ mechanism on soft substrates and the ‘frictional slippage’ mechanism on rigid substrates. In both cases, when the mechanical stress of the substrate reaches a certain point and some of the engaged molecular clutches dissociate due to the mechanical load, there is virtually no relaxation of the substrate mechanical stress, which redistributes among a smaller number of the remaining molecular clutches engaged to the substrate. Therefore, the tension of the remaining molecular clutches becomes higher, which leads to their rapid dissociation, the ‘fail’ event, when all molecular clutches dissociate and the substrate returns to its relaxed conformation (Fig. 6a,c).

Fig. 6: Load-and-fail mechanism versus differential-transmission mechanism.

a,b, Schematic representations of the load-and-fail mechanism (a) and the differential-transmission mechanism (b). The formation of molecular clutches results in transmission of the force generated by myosin II motors to the substrate, causing its deformation. In the load-and-fail mechanism, when the increasing tension of molecular clutches reaches a certain value, the molecular clutches dissociate in a highly cooperative manner as a result of their high rigidity, which is usually used in conventional molecular-clutch models (a). By contrast, in the models developed in our study (b), molecular clutches exhibit highly elastic properties, which is in good agreement with experiments. This leads to a loss of synchronization of the dissociation of molecular clutches under the myosin II-generated load, and as a result, the molecular-clutch system exhibits a more uniform behaviour, functioning as a differential transmission that mechanically couples the substrate and actin cytoskeleton, which are moving at different speeds. c–e, Stochastic kinetic simulations of the conventional molecular-clutch model (c) and our linear KD (d) and linear WT (e) models. The conventional molecular-clutch model predicts stochastic oscillations between zero and the maximum cell traction on soft substrates (load-and-fail mechanism). By contrast, the linear WT and linear KD models predict much milder fluctuations of the molecular-clutch system around its steady state, with the amplitude of fluctuations being smaller for softer molecular-clutch components (linear WT model) due to the differential-transmission mechanism schematically shown in b.

By contrast, in our model, molecular clutches are represented by highly elastic adaptor proteins (0.05–1.6 pN nm⁻¹) mechanically coupled through adhesion receptors to local substrate deformations at the adhesion sites of the molecular clutches. Cell traction and retrograde actin flow fluctuate around their steady-state values, which are determined by the force balance between the tension of adaptor proteins, local substrate deformations and the mechanical load created by myosin II motors (Fig. 6d,e). This behaviour of cell traction and retrograde actin flow is in better agreement with previous experiments compared to the load-and-fail and frictional slippage mechanisms⁴⁵. Indeed, the high elasticity of molecular clutches in our model results in dynamic frictional coupling between the substrate and retrograde actin flow for both soft and rigid substrates. Thus, the dissociation of some of the molecular clutches leads to a rapid redistribution of forces and a partial release of the substrate tension, so that the tension in the remaining molecular clutches is less than in the load-and-fail scenario. This makes it possible for the remaining molecular clutches to withstand the load long enough to allow new molecular clutches to form (Fig. 6b). As a result, the molecular-clutch system functions as a differential transmission that enables the retrograde actin flow and substrate to move at different speeds, while maintaining stable mechanical coupling between them. Notably, the amplitude of fluctuations experienced by the molecular-clutch system in this case strongly depends on both the elastic properties of the adaptor proteins and the assembly rate of molecular clutches, with the more elastic talin molecules demonstrating a greater ability to buffer substrate stress and deformations, resulting in fairly stable cell traction and retrograde actin flow, even on very rigid substrates, in good agreement with experimental observations^{7,13,21,30,42,43}.

Furthermore, the force-loading rate of talin-based molecular clutches predicted by the model (0.2–5.5 pN s⁻¹, rigid substrate) is in good agreement with experimental data (0.2–4 pN s⁻¹)^19,20. In addition, because the force-loading rate of molecular clutches is determined by the elasticity of their components, the model predicts that the nonlinear force response of talin will result in a higher force-loading rate of molecular clutches at higher tensions, whereas the vinculin-mediated locking of talin in the softer unfolded state is predicted to result in a low force-loading rate of molecular clutches even for the vinculin I997A mutant, which has reduced actin-binding ability. Both of these model predictions are in good agreement with direct experiment observations^19,20. These results demonstrate that the elasticity of adaptor proteins is one of the key factors that must be taken into account when relating the force response of molecular clutches at the single-molecule level to mesoscale cell behaviour.

In addition to the elasticity of molecular-clutch components, another important aspect considered in our model is the local deformation of the substrate at the attachment sites of molecular clutches (Figs. 1 and 6b). When individual integrins or small clusters of them exert a mechanical force on the substrate, elasticity theory predicts that only a small region of the substrate in the immediate vicinity will be most strongly deformed⁴⁶. Consistently, it has been widely reported in the literature that local changes in the traction force or substrate deformation on scales smaller than cell-adhesion complexes play a critical role in regulating the mechanosensitive behaviour of cell adhesion^20,45,47,48.

From a modelling perspective, if the substrate elasticity is represented by a spring describing its global deformation at the scale of cell-adhesion complexes, then it can be theoretically shown that for soft molecular clutches, the system will lose its ability to sense substrate rigidity and will always reach the same steady state (the same cell traction and retrograde actin flow), regardless of the substrate stiffness, unless some parameters of the system, such as cell contractility, are adaptively changed⁴⁹. In this scenario, the substrate remains relatively stationary at a nearly constant steady-state tension. As a result, the molecular clutches have no information about the degree of substrate deformation required to achieve the steady-state tension, and therefore, they cannot distinguish between different substrate stiffnesses.

By contrast, if local substrate deformations at the attachment sites of molecular clutches are considered, then the intracellular part (adaptor proteins) and the extracellular part (local substrate deformation) of each molecular clutch will establish their own individual force balance, which collectively determines the state of larger cell-adhesion complexes. In this case, the overall rigidity of local substrate deformations and adaptor proteins will influence the force-loading dynamics and the lifetime of molecular clutches, allowing the system to reach different substrate-dependent steady states. Consequently, our model can robustly predict the mechanosensitive response of cell-adhesion complexes over a wide range of substrate rigidities without the need for any rigidity-dependent adjustments to the physiological parameters of the system. Thus, we propose that the sensing of substrate rigidity at the molecular level, where each molecular clutch probes the mechanical properties of its local substrate by establishing its own force balance, is critical for the mechanosensitive cell-adhesion response.

Our model also predicts that when the adaptor proteins and substrate have high stiffnesses (k_c ≳ 0.5–0.8 pN nm⁻¹ and E ≳ 100 kPa), the molecular-clutch system exhibits bistable behaviour, in which both weak and strong cell-adhesion states are stable at the same value of substrate elasticity. From a physical point of view, this is reminiscent of the previously reported bistable cytoadhesion properties of malaria-infected red blood cells^50,51. Bistability can potentially arise at the level of a single cell or individual FAs. It is influenced by the heterogeneity and topography of the ECM ligand network, which affect the local density of sites available for forming molecular clutches and the rate of molecular-clutch assembly. This, in turn, influences the tension experienced by molecular clutches and actin filaments, also potentially altering the mechano-dependent cooperative assembly of myosin IIA and myosin IIB stacks regulated by ROCK, MLCK⁵² and PKCz⁵³.

The quasi-static nature of molecular-clutch kinetics and the emergence of bistable cell-adhesion behaviour revealed in our model indicate that, for a given substrate rigidity, several stable states of molecular clutches can coexist. This means that our model can, in principle, be used as a theoretical basis to describe the maturation process of FAs, in which small NAs are gradually transformed into mature FAs with a different molecular composition, molecular-clutch density and traction force, despite being in the same extracellular environment. In this context, the maturation of FAs can be viewed as a series of quasi-steady states, each of which represents a snapshot of maturing cell adhesion. Changes in the physiological parameters describing mechanical or biochemical processes, such as local molecular-clutch density and elasticity and myosin II contractility, collectively model the evolution of the quasi-steady-state behaviour of FAs towards more mature states. In addition, the bistability of cell adhesion found in our work may also explain why only a small fraction of NAs mature on rigid substrates whereas the rest disassemble, which warrants future study.

Note that in our study, we considered the unfolding of the mechanosensitive R3 domain of talin. Yet, the force-induced unfolding of other domains may also stabilize the tension experienced by talin and influence molecular-clutch stability, indicating a broader role for adaptor-protein elasticity^54,55. Understanding how the unfolding of talin domains and other adaptor proteins regulates mechanosensitive cell-adhesion behaviour remains an important question that may be potentially clarified by integrating our model with molecular dynamics simulations⁵⁶.

Similarly, one of the critical missing links in existing molecular-clutch models is how the dynamic behaviour of cell-adhesion complexes is involved in the interplay with other cell mechanosensing mechanisms that influence cell-adhesion behaviour. For example, mechanosensitive ion channels^57,58,59, formins^{1,60,61,62,63} and LIM domain proteins⁶⁴ have been shown to potentially play important roles in regulating the force response of FAs or the cell-signalling cascades involved in remodelling cell-adhesion complexes. With more accurate and realistic modelling of the conformational states of molecular-clutch proteins, which is possible within our model, one can begin to quantitatively investigate the complex interactions between these mechanosensitive processes at the molecular level, as they have important consequences for many physiological processes, from morphogenesis to cancer progression.

Finally, in addition to substrate stiffness, the rheological properties of the ECM, such as viscoelasticity, have also been shown to be an important regulator of cellular functions and are known to be related to pathological processes of tumour growth and metastasis. There have been several interesting attempts to model the mechanosensitive behaviour of cells on viscoelastic substrates based on the conventional molecular-clutch theory. These have successfully reproduced various cell behaviours, such as periodic oscillations in cell spreading and cell migration^{10,14,16,17,18}. In the future, it will be interesting to combine our semi-analytic model with these previous studies to explore how physiological factors, such as the stiffness of molecular-clutch components, regulate these important cell behaviours.

Methods

Linear molecular-clutch model

In this study, we use the model shown schematically in Fig. 1b. Molecular clutches are represented by springs consisting of two parts: (1) cellular, corresponding to adaptor proteins, and (2) extracellular, describing local substrate deformations at the adhesion sites of molecular clutches. In the simplest case, these two parts of the molecular clutches can be described by linear springs with spring constants k_c and ${k}_{{\rm{s}}}^{{\prime} }$, respectively.

In addition to local substrate deformation at the adhesion sites of molecular clutches, the model also takes into account the average substrate deformation over a much larger area of cell-adhesion complexes with a characteristic size R. This type of substrate deformation is described in the model by the spring constant k_s shown in Fig. 1b.

Using the theory of elasticity, it can be shown that the spring constant ${k}_{{\rm{s}}}^{{\prime} }$ describing local substrate deformations is related to the Young’s modulus of the substrate (E) as (Supplementary Appendix A):

$${k}_{{\rm{s}}}^{{\prime} }(E)=\frac{4\uppi rE}{9},$$

(1)

where r is the characteristic size of the adhesion site of a single molecular clutch.

The spring constant k_s describes large-scale substrate deformations. In general, it depends both on the Young’s modulus of the substrate and on the shape of cell-adhesion complexes: k_s = k_s(E, shape). For example, if the shapes of cell-adhesion complexes can be approximated by ellipses, then k_s(E) = 4πRE/9, where R = a/I_e(e_c) is the characteristic size of the cell-adhesion complexes. Here a and e_c are the major axis and eccentricity of the ellipse representing the shape of the cell-adhesion complexes, and I_e is an elliptic integral whose value as a function of the ellipse eccentricity is shown in Supplementary Fig. 3a (see also Supplementary Appendix A). Thus, like ${k}_{{\rm{s}}}^{{\prime} }$, k_s in this case is proportional to the characteristic size of cell-adhesion complexes, R. As a result, taking into account the experimentally measured characteristic size of FAs (R ≈ 1.7 μm)¹³ and the typical size of the binding sites of adhesion receptors (up to several nanometres), it follows that local substrate deformations at the adhesion sites of molecular clutches should be much greater than the average deformation of the substrate on the FA scale and, consequently, have a much stronger effect on the dissociation kinetics of molecular clutches compared to the average substrate deformation. Moreover, as shown below, the main results of our study are essentially independent of the spring constant k_s and its exact functional form, because it is absent from the main formulae determining the steady-state behaviour of the molecular-clutch system.

To describe the dynamic state of the system, the sites available for molecular-clutch formation are divided into two groups in the model: those that are occupied by molecular clutches (on state) and those that are not (off state).

In addition, each molecular clutch is characterized by its own deformation resulting from the mechanical load F_m generated by myosin II motors (Fig. 1b). Super-resolution images of the nanoscale architecture of FAs show that the average contact angle of the intracellular part of molecular clutches with the cell membrane or substrate surface, θ, is very small (θ ≈ 15°; ref. ⁶⁵; see the schematic in Fig. 1b). Thus, molecular clutches experience much greater deformation along the x axis parallel to the substrate surface compared to the z axis perpendicular to it. As a result, the physical state of each molecular clutch can be described to a first approximation by its extension, l, along the x axis parallel to the substrate surface, which includes the mechanical deformation of both the intracellular and extracellular parts of the molecular clutch (Fig. 1b). Accordingly, the state of the entire system can be represented by a time-dependent probability distribution p_on(l, t) of observing a molecular clutch with extension l at time t, for each site available for molecular-clutch formation. This distribution satisfies the following normalization condition:

$${p}_{{\rm{off}}}(t)+\int_{-\infty }^{+\infty }{p}_{{\rm{on}}}(l,t)\,{\rm{d}}l=1$$

(2)

where p_off(t) is the time-dependent probability of the off state. The extension of a molecular clutch can be positive or negative, depending on the orientation of the molecular clutch along the x axis.

When formed, molecular clutches should have an extension randomly distributed around the mechanically relaxed state, with a peak corresponding to zero extension along the x axis (l = 0). As a result, the extension-dependent assembly rate of molecular clutches k_on(l) can be approximated using the Dirac δ function δ(l):

$${k}_{{\rm{on}}}(l)={k}_{{\rm{on}}}^{0}\delta (l),$$

(3)

where ${k}_{{\rm{on}}}^{0}$ is a constant.

A retrograde flow of actin filaments created by myosin II motors results in a gradual stretching of molecular clutches. This, in turn, leads to an increase in their deformation, causing subsequent dissociation. We assumed in this study that the dissociation of molecular clutches is mainly driven by the detachment of integrins from their ECM ligands, such as fibronectin. Indeed, previous studies have indicated that this may be the weakest point of molecular clutches, as the bonds between other molecular-clutch components seem to be substantially strengthened by an applied mechanical load^37,41,66. For example, talin has a multivalent association with the actin cytoskeleton mediated by talin-bound vinculins, which form catch bonds with F-actin that exhibit force-dependent enhancement⁴¹. This model assumption is further supported by recent DNA tension-gauge tether experiments showing that individual molecular clutches can withstand forces >10 pN for tens of seconds, far exceeding previous estimates based on the experimentally measured strength of talin–actin bonds^39,41. Because integrin–ECM bonds have previously been shown to exhibit catch-bond behaviour, exhibiting force-dependent bond enhancement in the range 0–30 pN and force-induced bond dissociation at higher forces⁶⁷, the dissociation rate of molecular clutches (k_off) was approximated by the following two-term exponential formula, which was found to fit the experimental data very well (Supplementary Fig. 4):

$${k}_{{\rm{off}}}(F)={k}_{{\rm{off}}}^{0}\operatorname{e}^{\beta {x}_{{\rm{t}}}| F| }+{k}_{{\rm{off}}}^{{0}^{{\prime} }}\operatorname{e}^{\beta {x}_{{\rm{t}}}^{{\prime} }| F| },$$

(4)

where x_t and ${x}_{{\rm{t}}}^{{\prime} }$ are two transition state distances characterizing the force-dependent behaviour of the integrin–ECM catch bond, and ${k}_{{\rm{off}}}^{0}$ and ${k}_{{\rm{off}}}^{{0}^{{\prime} }}$ are the corresponding dissociation rates at zero mechanical load. β = 1/k_BT is the reciprocal of the thermodynamic temperature, where k_B is the Boltzmann constant. ∣F∣ is the absolute value of the tension applied to the bond.

For molecular clutches represented by two-part linear springs, the force–extension behaviour of each molecular clutch is described by

$$F(l)=k(E)\,l=\frac{{k}_{{\rm{c}}}{k}_{{\rm{s}}}^{{\prime} }(E)}{{k}_{{\rm{c}}}+{k}_{{\rm{s}}}^{{\prime} }(E)}\,l,$$

(5)

where $k={k}_{{\rm{c}}}{k}_{{\rm{s}}}^{{\prime} }/({k}_{{\rm{c}}}+{k}_{{\rm{s}}}^{{\prime} })$ is the resulting spring constant of molecular clutches consisting of the two parts: extracellular (${k}_{{\rm{s}}}^{{\prime} }$) and intracellular (k_c) (Fig. 1b).

Given the probability distribution p_on(l, t), then the total tension of molecular clutches or, what is the same, the traction force created by molecular clutches within a single cell-adhesion complex, F_c(t) (Fig. 1b), can be found as:

$${F}_{{\rm{c}}}(t)={N}_{{\rm{c}}}\int_{-\infty }^{+\infty }F(l)\,{p}_{{\rm{on}}}(l,t)\,{\rm{d}}l,$$

(6)

where N_c is the number of sites available for the formation of molecular clutches in the cell-adhesion complex. Recent experimental studies show that the average density of talin and, probably therefore, the density of sites available for molecular-clutch formation are very similar in both small and large FAs²⁷, indicating that these are independent of the size of the FAs. As a result, we concluded that N_c is proportional to the area of the cell-adhesion complexes S: N_c = σ_cS, where σ_c is the average density of sites available for the formation of molecular clutches in a cell-adhesion complex.

According to the Newton’s third law, the total tension in engaged molecular clutches (F_c) is equal to the force generated by myosin II motors: F_m(t) = F_c(t). Following previous studies^{7,11,12,13,14}, the resisting effect of such a load on the movement rate of myosin II motors, v(t), is approximated by a linear force–velocity relation:

$$v(t)={v}_{0}\left[1-\frac{{F}_{{\rm{m}}}(t)}{{N}_{{\rm{m}}}{F}_{{\rm{st}}}}\right],$$

(7)

where F_st is the stalling force of a single myosin II motor. v₀ is the movement rate of myosin II motors at zero mechanical load. N_m is the number of myosin motors pulling actin filaments within a cell-adhesion complex. Because previous studies indicated that myosin II motors exert a local pulling effect on the actin cytoskeleton in the cell cortex⁴², we assumed in the model that N_m is proportional to the area of cell-adhesion complexes: N_m = σ_mS, where σ_m is the average surface density of myosin II motors near the cell–substrate interface.

Experimental studies show that actin filaments exhibit retrograde movement at nearly constant rates (v(t) ≈ const.)^{7,13,21,42,43}. Thus, it can be concluded that myosin II motors and the entire ensemble of molecular clutches function close to a steady state in living cells. This makes it possible to derive a system of simple equations that describe the long-term steady-state behaviour of the entire ensemble of molecular clutches and myosin II motor proteins based on the above formulae (Supplementary Appendix B):

$$\begin{cases}\frac{\partial {p}_{{\rm{on}}}(l\,)}{\partial l}=-\frac{{k}_{{\rm{off}}}(l)}{v}\,{p}_{{\rm{on}}}(l),\;\text{if}\;l>0,\\{p}_{{\rm{on}}}(l)=0,\;\text{if}\;l< 0,\\{\displaystyle{\int}}_{0}^{+\infty}{k}_{{\rm{off}}}(l\,)\,{p}_{{\rm{on}}}(l)\,{\rm{d}}l={k}_{{\rm{on}}}^{0}\,{p}_{{\rm{off}}},\\{F}_{{\rm{c}}}={N}_{{\rm{c}}}{\displaystyle{\int}}_{0}^{+\infty}F(l)\,{p}_{{\rm{on}}}(l)\,{\rm{d}}l={N}_{{\rm{m}}}{F}_{{\rm{st}}}\left[1-\frac{v}{{v}_{0}}\right]={F}_{{\rm{m}}},\\{x}_{{\rm{s}}}=\frac{{F}_{{\rm{c}}}}{{k}_{{\rm{s}}}}.\end{cases}$$

(8)

The first line of the equation describes the time-averaged probability distribution p_on(l) = 〈p_on(l,t)〉_T of molecular-clutch extension, which is determined by the force-dependent dissociation rate of molecular clutches, k_off(l) = k_off(F(l)), and the retrograde actin flow, v. The second line simply states that in a steady state, molecular clutches are stretched in one direction by retrograde actin flow. The third line indicates that in a steady state, the total probability flux due to the dissociation of molecular clutches is balanced by the probability flux due to their formation, which provides the normalization condition for the p_on(l) probability distribution. The fourth line represents Newton’s third law, which states that the total tension in engaged molecular clutches (F_c) is equal to the force generated by myosin II motors (F_m). Finally, the fifth line of the equation shows the average mechanical deformation of the substrate (x_s) in a steady state due to the traction force (F_c) (Fig. 1b).

To determine the long-term behaviour of the molecular-clutch system and fit the experimental data, we solved equation (8) in terms of p_on, F_c and v and then compared the calculated values of cell traction (F_c) and retrograde actin flow (v) to experimental measurements. To do this, equation (8) was solved by finding the intersections of the graphs of F_c(v) and F_m(v). This allowed us not only to construct a simple geometric interpretation of solutions to equation (8) but also to assess their stability (Extended Data Fig. 1).

Specifically, F_m(v) can be directly calculated from the fourth line of equation (8). On the other hand, the computation of F_c(v) requires knowledge of the probability distribution p_on(l), which can be found from the first three lines of equation (8) (Supplementary Appendix C):

$${p}_{{\rm{on}}}(l)=\frac{{k}_{{\rm{on}}}^{0}\exp({-(1/v)\int_{0}^{l}{k}_{{\rm{off}}}({l}^{{\prime}})\,{\rm{d}}{l}^{{\prime} }})}{v+{k}_{{\rm{on}}}^{0}{\displaystyle{\int}}_{0}^{+\infty}\exp({-(1/v){\int}_{0}^{{l}^{{\prime}}}{k}_{{\rm{off}}}({l}^{{\prime}{\prime}})\,{\rm{d}}{l}^{{\prime}{\prime}}})\,{\rm{d}}{l}^{{\prime}}},\qquad{l}> 0.$$

(9)

Knowing the p_on(l) distribution, the total tension of molecular clutches (F_c) can easily be obtained from equation (8) as a function of the retrograde actin flow speed (v), which leads to the solution of equation (8).

To compare the cell traction force predicted by the model (F_c) with experimental measurements, we calculated the traction stress (P) exerted by cell-adhesion complexes on the substrate:

$$P=\frac{{F}_{{\rm{c}}}}{S},$$

(10)

where S is the area of the cell-adhesion complexes.

Notably, as can be seen from equations (4)–(10), in the steady state, cell traction and the retrograde actin flow are determined by local substrate deformations at the sites of molecular-clutch attachment, which are described in the model by the spring constant ${k}_{{\rm{s}}}^{{\prime} }$ (Supplementary Appendix D) and do not depend on the spring constant k_s describing large-scale substrate deformations on the scale of cell-adhesion complexes. Thus, we concluded that cell traction, retrograde actin flow and the average tension of molecular clutches do not depend on the size and shape of cell-adhesion complexes in the steady state (Supplementary Fig. 3b–e and Supplementary Appendix E), which is in good agreement with experimental data showing that the average density of talin molecules in FAs and their average tension are, indeed, independent of FA size²⁷.

Finally, note that although in the above equations we considered molecular clutches to be simply represented by linear springs, the resulting equations (8)–(10) are very general, as an arbitrary force response of molecular clutches can be used in the model. For example, to describe nonlinear deformations of molecular clutches caused by reversible force-induced unfolding of their globular protein domains or the desorption of ECM from the substrate^68,69, another parameter can be introduced into the model, the extension l_y of molecular clutches, at which their linear behaviour switches to nonlinear behaviour. Thus, we change equation (5) to:

$$F(l)=\begin{cases}kl,&\text{if}\;l\le {l}_{{\rm{y}}},\\ k{l}_{{\rm{y}}},&{\rm{otherwise}}.\end{cases}$$

(11)

This coarse-grained approach is most suitable for describing molecular clutches with an unknown architecture or protein structure.

On the other hand, if the structure and mechanical stability of the main molecular-clutch components are known, more detailed information can be obtained compared to the above approach by considering all possible transitions between different folded and unfolded states of molecular clutches. We used this method to account for the highly nonlinear behaviour of talin molecules and the force-induced unfolding of the mechanosensitive talin domain (R3) observed in single-molecule experiments²² (Supplementary Appendix F).

Importantly, almost all model parameters can be measured experimentally (Supplementary Table 1). Regarding the remaining parameters, by simultaneously fitting experimental data obtained under different experimental conditions (WT or talin-deficient cells that are either treated with myosin II inhibitor or grown on substrates coated with different concentrations of fibronectin, as described in ‘Results’), the average number of fitting parameters per curve can be reduced to one or two, so that fitting the experimental data to the model is very robust. A list of key model-fitting parameters used in this study can be found in Extended Data Table 2.

Cell lines, constructs and experimental data processing

Cell culture, constructs and transfection

NIH-3T3 and HeLa cells were obtained from the laboratory of Q. Peng (Shenzhen Bay Laboratory, China). All cell lines were grown in Dulbecco’s modified Eagle’s medium (Gibco, C11995500BT) supplemented with 10% fetal bovine serum (Gibco, 10099-141C) and 1% penicillin/streptomycin (Gibco, 15070-063) at 37 °C under 5% CO₂.

To visualize myosin II motors, cells were transfected with a plasmid encoding myosin RLC-GFP (gift from A. Bershadsky, Mechanobiology Institute, Singapore) using jetPRIME buffer (Polyplus, 712-60) and jetPRIME reagent (Polyplus, 114-15) according to the manufacturer’s instructions. Following the transfection, cells were seeded onto 35-mm glass-bottomed dishes coated with 1, 10 or 100 μg ml⁻¹ fibronectin (Solarbio, F8180) dissolved in Dulbecco’s phosphate-buffered saline (DPBS, Gibco, C14190500BT). The day after transfection, cells were fixed for 15 min with 4% paraformaldehyde solution (Beyotime, P0099), followed by washing with DPBS (three times), after which the cells were imaged.

To visualize vinculin and talin, NIH-3T3 cells were transfected with plasmids encoding mCherry-Vinculin (gift from K. Yamada, Addgene 50527) and GFP-Talin 1 (gift from A. Huttenlocher, Addgene 26724) using Lipofectamine 3000 Transfection Reagent (Thermo Fisher Scientific). The next day, the cells were replated into glass-bottomed dishes coated with 10 μg ml⁻¹ fibronectin (Corning) and imaged.

Fluorescence microscopy

Cells transfected with the myosin RLC-GFP construct were imaged using an ultra-high resolution microscope (Elyra 7, Zeiss) equipped with Plan Apochromatic ×63/1.4 oil differential interference contrast objective, which was controlled by software ZEN (black edition). During the experiment, the microscope was focused on the ventral side of the transfected cells, resulting in images of predominantly ventral myosin II motors. The images were captured with a pco.edge sCMOS camera (Lattice SIM module) and processed by the Lattice SIM2 structured illumination technique (horizontal resolution of 60 nm and axial resolution of 200 nm). Fluorescence was excited using optically pumped semiconductor lasers (488 nm at 500 mW and 561 nm at 500 mW). Cells transfected with mCherry-Vinculin and GFP-Talin 1 were imaged every 2 s for 4,000 s after 6 h of spreading using a total internal reflection fluorescence microscope (Nikon Ti2) equipped with a standard set of lasers and filters.

Image analysis and statistics

Collected images of RLC-GFP-labelled myosin II stacks were analysed with the help of ImageJ-win64 software. To do this, several random regions near the cell corners were selected for each cell and automatic thresholding was applied using the built-in Auto Threshold function of ImageJ to map the contours of myosin II filament stacks. The resulting images were further processed with the Analyze Particles function, which provided the total number and sizes of the detected myosin II filament stacks. After discarding all particles with an area less than 0.01 μm², the average density and the average size of myosin II filament stacks as well as the corresponding s.e.m. were calculated. All experimental results presented in the article are representative of three independent experiments. Statistical analyses of the data were carried out using the one-way ANOVA with post-hoc Tukey’s honestly significant difference test.

Images of mCherry-Vinculin and GFP-Talin 1 cells were registered in ImageJ using the descriptor-based registration plugin⁷⁰. The images were then cropped and scaled down by a factor of 0.75 in the x and y directions and by a factor of 0.5 in time. Segmenting, tracking and measuring the area of FAs and measuring the average intensities of talin and vinculin were carried out using the FAA server⁷¹ with a minimum FA size of 0.1 μm² (Extended Data Fig. 8a). The tracked FAs were then filtered in MATLAB (Mathworks) to remove tracks with lifetimes of less than 5 min and tracks in which the size of the FAs exceeded 0.5 μm² in more than three of the first five frames to remove tracks in which FAs were already mature when detected. This left only tracks corresponding to NAs. After this, all NAs were divided into two groups: peripheral NAs and central NAs. To identify peripheral and central NAs, the mask of each cell was eroded using a 4.3-μm-diameter disc. Those NAs whose centroid fell into this remaining region in the first frame they appeared in were considered central, and those that formed outside this region were considered to be peripheral (Extended Data Fig. 8b). The resulting mCherry-Vinculin and GFP-Talin 1 signal intensities measured within peripheral NAs were normalized to the first frame for each NA and then averaged over all peripheral NAs (Extended Data Fig. 8d,e). The mean integral intensity as a function of time was calculated by multiplying the mean normalized intensity by the mean area of NAs (Extended Data Fig. 8c). To estimate the mean integral intensity of talin-bound vinculins in peripheral NAs, the mean integral intensity of vinculin in each NA was offset by the initial value, because experimental studies show that the initial accumulation of vinculin in NAs occurs predominantly due to the binding of vinculin to paxillin and not to mechanically unfolded talin⁷². The resulting integral intensities of talin and talin-bound vinculin measured in peripheral NAs in the experiments were then compared with model predictions (Fig. 4b).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.