Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Magnon-polarons in the Fermi–Hubbard model

Nature Physics (2025)Cite this article

Subjects

Abstract

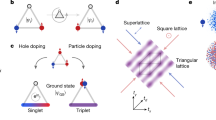
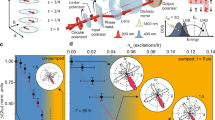
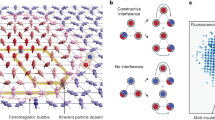
The interplay of magnetic excitations and itinerant charge carriers is a ubiquitous phenomenon in strongly correlated electron systems. A key theoretical question is understanding the renormalization of the magnon quasiparticle, a collective spin excitation, upon doping a magnetic insulator. Here we observe a new type of quasiparticle—a magnon-Fermi-polaron—arising from the dressing of a magnon with the doped holes of a cold-atom Fermi–Hubbard system. Using Raman excitation with controlled momentum in a doped, spin-polarized band insulator, we address the spectroscopic properties of the magnon-polaron. In an undoped system with strong interactions, photoexcitation produces magnons, whose properties are accurately described by spin-wave theory. We measure the evolution of the photoexcitation spectra as we move away from this limit to produce magnon-polarons due to dressing of the magnons by charge excitations. We observe a shift in the polaron energy with doping that is strongly dependent on the injected momentum, accompanied by a reduction of spectral weight in the probed energy window. We anticipate that the technique introduced here, which is the analogue of inelastic neutron scattering, will provide atomic quantum simulators with access to the dynamics of a wide variety of excitations in strongly correlated phases.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Raman spectroscopy of a Fermi–Hubbard system.
Fig. 2: Interaction dependence of the quasiparticle energy.
Fig. 3: Doping dependence of the magnon-polaron energy.
Fig. 4: Magnon-polaron dispersion and effective mass.

Similar content being viewed by others

Data availability

The experimental data are available from the corresponding author upon reasonable request. Source data are provided with this paper.

Code availability

The relevant codes for this work are available from the corresponding author upon reasonable request.

References

  1. Scalapino, D. J., Loh, E. & Hirsch, J. E. d-wave pairing near a spin-density-wave instability. Phys. Rev. B 34, 8190–8192 (1986).

    Article  ADS  Google Scholar 

  2. Scalapino, D. J., Loh, E. & Hirsch, J. E. Fermi-surface instabilities and superconducting d-wave pairing. Phys. Rev. B 35, 6694–6698 (1987).

    Article  ADS  Google Scholar 

  3. Anderson, P. W. The resonating valence bond state in La2CuO4 and superconductivity. Science 235, 1196–1198 (1987).

    Article  ADS  Google Scholar 

  4. Gros, C., Joynt, R. & Rice, T. M. Antiferromagnetic correlations in almost-localized Fermi liquids. Phys. Rev. B 36, 381–393 (1987).

    Article  ADS  Google Scholar 

  5. Zhang, F. C. & Rice, T. M. Effective Hamiltonian for the superconducting Cu oxides. Phys. Rev. B 37, 3759–3761 (1988).

    Article  ADS  Google Scholar 

  6. Zhang, F. C., Gros, C., Rice, T. M. & Shiba, H. A renormalised Hamiltonian approach to a resonant valence bond wavefunction. Supercond. Sci. Technol. 1, 36 (1988).

    Article  ADS  Google Scholar 

  7. Kotliar, G. & Liu, J. Superexchange mechanism and d-wave superconductivity. Phys. Rev. B 38, 5142–5145 (1988).

    Article  ADS  Google Scholar 

  8. Schrieffer, J. R., Wen, X.-G. & Zhang, S.-C. Spin-bag mechanism of high-temperature superconductivity. Phys. Rev. Lett. 60, 944–947 (1988).

    Article  ADS  Google Scholar 

  9. Monthoux, P., Balatsky, A. V. & Pines, D. Toward a theory of high-temperature superconductivity in the antiferromagnetically correlated cuprate oxides. Phys. Rev. Lett. 67, 3448–3451 (1991).

    Article  ADS  Google Scholar 

  10. Monthoux, P., Balatsky, A. V. & Pines, D. Weak-coupling theory of high-temperature superconductivity in the antiferromagnetically correlated copper oxides. Phys. Rev. B 46, 14803–14817 (1992).

    Article  ADS  Google Scholar 

  11. Dai, P., Mook, H. A., Hunt, R. D. & Doğan, F. Evolution of the resonance and incommensurate spin fluctuations in superconducting YBa2Cu3O6+x. Phys. Rev. B 63, 054525 (2001).

    Article  ADS  Google Scholar 

  12. Anderson, P. W. et al. The physics behind high-temperature superconducting cuprates: the ‘plain vanilla’ version of RVB. J. Phys. Condens. Matter 16, R755 (2004).

    Article  Google Scholar 

  13. Anderson, P. W. Physics of the resonating valence bond (pseudogap) state of the doped Mott insulator: spin-charge locking. Phys. Rev. Lett. 96, 017001 (2006).

    Article  ADS  Google Scholar 

  14. Edegger, B., Muthukumar, V. N. & Gros, C. Gutzwiller-RVB theory of high-temperature superconductivity: results from renormalized mean-field theory and variational Monte Carlo calculations. Adv. Phys. 56, 927–1033 (2007).

    Article  ADS  Google Scholar 

  15. Dahm, T. et al. Strength of the spin-fluctuation-mediated pairing interaction in a high-temperature superconductor. Nat. Phys. 5, 217–221 (2009).

    Article  Google Scholar 

  16. Le Tacon, M. et al. Intense paramagnon excitations in a large family of high-temperature superconductors. Nat. Phys. 7, 725–730 (2011).

    Article  Google Scholar 

  17. Dean, M. P. M. et al. Persistence of magnetic excitations in La2−xSrxCuO4 from the undoped insulator to the heavily overdoped non-superconducting metal. Nat. Mater. 12, 1019–1023 (2013).

    Article  ADS  Google Scholar 

  18. Lu, H. et al. Magnetic excitations in infinite-layer nickelates. Science 373, 213–216 (2021).

    Article  ADS  Google Scholar 

  19. Fowlie, J. et al. Intrinsic magnetism in superconducting infinite-layer nickelates. Nat. Phys. 18, 1043–1047 (2022).

    Article  Google Scholar 

  20. Miyake, K., Schmitt-Rink, S. & Varma, C. M. Spin-fluctuation-mediated even-parity pairing in heavy-fermion superconductors. Phys. Rev. B 34, 6554–6556 (1986).

    Article  ADS  Google Scholar 

  21. Mathur, N. D. et al. Magnetically mediated superconductivity in heavy fermion compounds. Nature 394, 39–43 (1998).

    Article  ADS  Google Scholar 

  22. White, B., Thompson, J. & Maple, M. Unconventional superconductivity in heavy-fermion compounds. Physica C 514, 246–278 (2015).

    Article  ADS  Google Scholar 

  23. Zhou, H. et al. Isospin magnetism and spin-polarized superconductivity in Bernal bilayer graphene. Science 375, 774–778 (2022).

    Article  ADS  Google Scholar 

  24. de la Barrera, S. C. et al. Cascade of isospin phase transitions in Bernal-stacked bilayer graphene at zero magnetic field. Nat. Phys. 18, 771–775 (2022).

    Article  Google Scholar 

  25. Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).

    Article  ADS  Google Scholar 

  26. Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).

    Article  ADS  Google Scholar 

  27. Chen, G. et al. Tunable correlated Chern insulator and ferromagnetism in a moiré superlattice. Nature 579, 56–61 (2020).

    Article  ADS  Google Scholar 

  28. Tang, Y. et al. Simulation of Hubbard model physics in WSe2/WS2 moiré superlattices. Nature 579, 353–358 (2020).

    Article  ADS  Google Scholar 

  29. Ciorciaro, L. et al. Kinetic magnetism in triangular moiré materials. Nature 623, 509–513 (2023).

    Article  ADS  Google Scholar 

  30. Tang, Y. et al. Evidence of frustrated magnetic interactions in a Wigner–Mott insulator. Nat. Nanotechnol. 18, 233–237 (2023).

    Article  ADS  Google Scholar 

  31. Xia, Y. et al. Superconductivity in twisted bilayer WSe2. Nature 637, 833–838 (2025).

  32. Scalapino, D. J. A common thread: the pairing interaction for unconventional superconductors. Rev. Mod. Phys. 84, 1383–1417 (2012).

    Article  ADS  Google Scholar 

  33. Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).

    Article  ADS  Google Scholar 

  34. Migdal, A. B. Interaction between electrons and lattice vibrations in a normal metal. Sov. Phys. JETP 34, 996–1001 (1958).

    Google Scholar 

  35. Eliashberg, G. M. Interactions between electrons and lattice vibrations in a superconductor. Sov. Phys. JETP 11, 696–702 (1960).

    MathSciNet  Google Scholar 

  36. Bourges, P. et al. The spin excitation spectrum in superconducting YBa2Cu3O6.85. Science 288, 1234–1237 (2000).

    Article  ADS  Google Scholar 

  37. Tranquada, J. M. et al. Quantum magnetic excitations from stripes in copper oxide superconductors. Nature 429, 534–538 (2004).

    Article  ADS  Google Scholar 

  38. Hayden, S. M., Mook, H. A., Dai, P., Perring, T. G. & Doğan, F. The structure of the high-energy spin excitations in a high-transition-temperature superconductor. Nature 429, 531–534 (2004).

    Article  ADS  Google Scholar 

  39. Wakimoto, S. et al. Disappearance of antiferromagnetic spin excitations in overdoped La2−xSrxCuO4. Phys. Rev. Lett. 98, 247003 (2007).

    Article  ADS  Google Scholar 

  40. Braicovich, L. et al. Dispersion of magnetic excitations in the cuprate La2CuO4 and CaCuO2 compounds measured using resonant x-ray scattering. Phys. Rev. Lett. 102, 167401 (2009).

    Article  ADS  Google Scholar 

  41. Braicovich, L. et al. Magnetic excitations and phase separation in the underdoped La2−xSrxCuO4 superconductor measured by resonant inelastic x-ray scattering. Phys. Rev. Lett. 104, 077002 (2010).

    Article  ADS  Google Scholar 

  42. Ament, L. J. P., van Veenendaal, M., Devereaux, T. P., Hill, J. P. & van den Brink, J. Resonant inelastic x-ray scattering studies of elementary excitations. Rev. Mod. Phys. 83, 705–767 (2011).

    Article  ADS  Google Scholar 

  43. Chaix, L. et al. Resonant inelastic x-ray scattering studies of magnons and bimagnons in the lightly doped cuprate La2−xSrxCuO4. Phys. Rev. B 97, 155144 (2018).

    Article  ADS  Google Scholar 

  44. Devereaux, T. P. & Hackl, R. Inelastic light scattering from correlated electrons. Rev. Mod. Phys. 79, 175–233 (2007).

    Article  ADS  Google Scholar 

  45. Fujita, M. et al. Progress in neutron scattering studies of spin excitations in high-Tc cuprates. J. Phys. Soc. Jpn 81, 011007 (2012).

    Article  ADS  Google Scholar 

  46. Ji, G. et al. Coupling a mobile hole to an antiferromagnetic spin background: transient dynamics of a magnetic polaron. Phys. Rev. X 11, 021022 (2021).

    Google Scholar 

  47. Koepsell, J. et al. Imaging magnetic polarons in the doped Fermi–Hubbard model. Nature 572, 358–362 (2019).

    Article  ADS  Google Scholar 

  48. Prichard, M. L. et al. Directly imaging spin polarons in a kinetically frustrated Hubbard system. Nature 629, 323–328 (2024).

    Article  ADS  Google Scholar 

  49. Lebrat, M. et al. Observation of Nagaoka polarons in a Fermi–Hubbard quantum simulator. Nature 629, 317–322 (2024).

    Article  ADS  Google Scholar 

  50. Hartke, T., Oreg, B., Turnbaugh, C., Jia, N. & Zwierlein, M. Direct observation of nonlocal fermion pairing in an attractive Fermi–Hubbard gas. Science 381, 82–86 (2023).

    Article  ADS  Google Scholar 

  51. Schirotzek, A., Wu, C.-H., Sommer, A. & Zwierlein, M. W. Observation of Fermi polarons in a tunable Fermi liquid of ultracold atoms. Phys. Rev. Lett. 102, 230402 (2009).

    Article  ADS  Google Scholar 

  52. Koschorreck, M. et al. Attractive and repulsive Fermi polarons in two dimensions. Nature 485, 619–622 (2012).

    Article  ADS  Google Scholar 

  53. Kohstall, C. et al. Metastability and coherence of repulsive polarons in a strongly interacting Fermi mixture. Nature 485, 615–618 (2012).

    Article  ADS  Google Scholar 

  54. Cetina, M. et al. Ultrafast many-body interferometry of impurities coupled to a Fermi sea. Science 354, 96–99 (2016).

    Article  ADS  Google Scholar 

  55. Yan, Z. Z., Ni, Y., Robens, C. & Zwierlein, M. W. Bose polarons near quantum criticality. Science 368, 190–194 (2020).

    Article  ADS  MathSciNet  Google Scholar 

  56. Ness, G. et al. Observation of a smooth polaron–molecule transition in a degenerate Fermi gas. Phys. Rev. X 10, 041019 (2020).

    Google Scholar 

  57. Parish, M. M. & Levinsen, J. Highly polarized Fermi gases in two dimensions. Phys. Rev. A 87, 033616 (2013).

    Article  ADS  Google Scholar 

  58. Jørgensen, N. B. et al. Observation of attractive and repulsive polarons in a Bose–Einstein condensate. Phys. Rev. Lett. 117, 055302 (2016).

    Article  ADS  Google Scholar 

  59. Hu, M.-G. et al. Bose polarons in the strongly interacting regime. Phys. Rev. Lett. 117, 055301 (2016).

    Article  ADS  Google Scholar 

  60. Darkwah Oppong, N. et al. Observation of coherent multiorbital polarons in a two-dimensional Fermi gas. Phys. Rev. Lett. 122, 193604 (2019).

    Article  ADS  Google Scholar 

  61. Duda, M. et al. Transition from a polaronic condensate to a degenerate Fermi gas of heteronuclear molecules. Nat. Phys. 19, 720–725 (2023).

    Article  Google Scholar 

  62. Zürn, G. et al. Precise characterization of 6Li Feshbach resonances using trap-sideband-resolved RF spectroscopy of weakly bound molecules. Phys. Rev. Lett. 110, 135301 (2013).

    Article  ADS  Google Scholar 

  63. Navarro, I. M., Weitenberg, C., Sengstock, K. & Demler, E. Exploring kinetically induced bound states in triangular lattices with ultracold atoms: spectroscopic approach. SciPost Phys. 16, 081 (2024).

    Article  ADS  MathSciNet  Google Scholar 

  64. Vaknin, D. et al. Antiferromagnetism in La2CuO4−y. Phys. Rev. Lett. 58, 2802 (1987).

    Article  ADS  Google Scholar 

  65. Fong, H. F. et al. Spin susceptibility in underdoped YBa2Cu3O6+x. Phys. Rev. B 61, 14773–14786 (2000).

    Article  ADS  Google Scholar 

  66. Fong, H. et al. Neutron scattering from magnetic excitations in Bi2Sr2CaCu2O8+δ. Nature 398, 588–591 (1999).

    Article  ADS  Google Scholar 

  67. Chevy, F. Universal phase diagram of a strongly interacting Fermi gas with unbalanced spin populations. Phys. Rev. A 74, 063628 (2006).

    Article  ADS  Google Scholar 

  68. Mora, C. & Chevy, F. Ground state of a tightly bound composite dimer immersed in a Fermi sea. Phys. Rev. A 80, 033607 (2009).

    Article  ADS  Google Scholar 

  69. Punk, M., Dumitrescu, P. T. & Zwerger, W. Polaron-to-molecule transition in a strongly imbalanced Fermi gas. Phys. Rev. A 80, 053605 (2009).

    Article  ADS  Google Scholar 

  70. Lovesey, S. W. Theory of Neutron Scattering from Condensed Matter (Oxford Univ. Press, 1984).

  71. Brown, P. T. et al. Spin-imbalance in a 2D Fermi–Hubbard system. Science 357, 1385–1388 (2017).

    Article  ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

We thank L. Cheuk for helpful discussions, and A. Hasan for assistance in early stages of this work. The experimental work was supported by the NSF (grant no. 2110475 and QLCI grant no. OMA-2120757), the David and Lucile Packard Foundation (grant no. 2016-65128) and the ONR (grant no. N00014-21-1-2646). M.L.P. was supported by the NSF Graduate Research Fellowship Program. D.A.H. was supported in part by NSF QLCI grant no. OMA-2120757. I.M. and E.D. were supported by the SNSF (project 200021_212899), the Swiss State Secretariat for Education, Research and Innovation (contract number UeM019-1) and the ARO (grant no. W911NF-20-1-0163).

Author information

Authors and Affiliations

  1. Department of Physics, Princeton University, Princeton, NJ, USA

    Max L. Prichard, Zengli Ba, Benjamin M. Spar, David A. Huse & Waseem S. Bakr

  2. Institute for Theoretical Physics, ETH Zürich, Zurich, Switzerland

    Ivan Morera & Eugene Demler

Authors
  1. Max L. Prichard
    View author publications

    Search author on:PubMed Google Scholar

  2. Zengli Ba
    View author publications

    Search author on:PubMed Google Scholar

  3. Ivan Morera
    View author publications

    Search author on:PubMed Google Scholar

  4. Benjamin M. Spar
    View author publications

    Search author on:PubMed Google Scholar

  5. David A. Huse
    View author publications

    Search author on:PubMed Google Scholar

  6. Eugene Demler
    View author publications

    Search author on:PubMed Google Scholar

  7. Waseem S. Bakr
    View author publications

    Search author on:PubMed Google Scholar

Contributions

M.L.P., Z.B. and B.M.S. performed the experiments and analysed the data. W.S.B. conceived the study and supervised the experiment. I.M., E.D. and D.A.H. developed the theory. I.M. performed the numerical calculations. All authors contributed to writing the paper.

Corresponding author

Correspondence to Waseem S. Bakr.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Ariel Sommer and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary text, Figs. 1–5 and refs. 1–12.

Source data

Source Data Fig. 1

Data for experimental axes (1d,e).

Source Data Fig. 2

Data for experimental axes (2a–c).

Source Data Fig. 3

Data for experimental axes (3a,b,d,e).

Source Data Fig. 4

Data for experimental axes (4c and inset).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Prichard, M.L., Ba, Z., Morera, I. et al. Magnon-polarons in the Fermi–Hubbard model. Nat. Phys. (2025). https://doi.org/10.1038/s41567-025-03004-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1038/s41567-025-03004-6

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing