Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Detection and characterization of targets in complex media using fingerprint matrices

Nature Physics (2025)Cite this article

Subjects

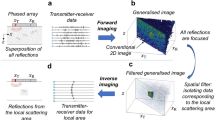
Abstract

When waves propagate through a complex medium, they undergo several scattering events. This phenomenon is detrimental to imaging, as it causes full blurring of the image. Here we describe a method for detecting, localizing and characterizing any scattering target embedded in a complex medium. We introduce a fingerprint operator that contains the specific signature of the target with respect to its environment. When applied to the recorded reflection matrix, it provides a likelihood index of the target state. This state can be the position of the target for localization purposes, its shape for characterization or any other parameter that influences its response. We demonstrate the versatility of our method by performing proof-of-concept ultrasound experiments on elastic spheres buried inside a strongly scattering granular suspension and on lesion markers, which are commonly used to monitor breast tumours, embedded in a foam mimicking soft tissue. Furthermore, we show how the fingerprint operator can be leveraged to characterize the complex medium itself by mapping the fibre architecture within muscle tissue. Our method is broadly applicable to different types of waves beyond ultrasound for which multi-element technology allows a reflection matrix to be measured.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Multiple-scattering fog.
Fig. 2: Detecting and localizing target metal spheres hidden in the multiple-scattering fog.
Fig. 3: Localizing a lesion marker in ultrasound speckle.
Fig. 4: Revealing the local architecture of fibres in muscle tissue.

Similar content being viewed by others

Data availability

The ultrasound data generated in this study are available via Zenodo at https://doi.org/10.5281/zenodo.14845779 (ref. 54).

Code availability

The code used to postprocess the ultrasound data within this paper is available via Zenodo at https://doi.org/10.5281/zenodo.14845779 (ref. 54).

References

  1. Fink, M. Time reversed acoustics. Phys. Today 50, 34 (1997).

    Article  Google Scholar 

  2. Mosk, A. P., Lagendijk, A., Lerosey, G. & Fink, M. Controlling waves in space and time for imaging and focusing in complex media. Nat. Photon. 6, 283 (2012).

    Article  ADS  Google Scholar 

  3. Foschini, G. & Gans, M. On limits of wireless communications in a fading environment when using multiple antennas. Wirel. Pers. Commun. 6, 311 (1998).

    Article  Google Scholar 

  4. Popoff, S. M. et al. Measuring the transmission matrix in optics: an approach to the study and control of light propagation in disordered media. Phys. Rev. Lett. 104, 100601 (2010).

    Article  ADS  Google Scholar 

  5. Prada, C. & Fink, M. Eigenmodes of the time reversal operator: a solution to selective focusing in multiple-target media. Wave Motion 20, 151 (1994).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  6. Popoff, S. M. et al. Exploiting the time-reversal operator for adaptive optics, selective focusing, and scattering pattern analysis. Phys. Rev. Lett. 107, 263901 (2011).

    Article  ADS  Google Scholar 

  7. Rotter, S. & Gigan, S. Light fields in complex media: mesoscopic scattering meets wave control. Rev. Mod. Phys. 89, 015005 (2017).

    Article  ADS  Google Scholar 

  8. Cao, H., Mosk, A. P. & Rotter, S. Shaping the propagation of light in complex media. Nat. Phys. 18, 994 (2022).

    Article  ADS  Google Scholar 

  9. Bertolotti, J. & Katz, O. Imaging in complex media. Nat. Phys. 18, 1008 (2022).

    Article  Google Scholar 

  10. Gérardin, B., Laurent, J., Derode, A., Prada, C. & Aubry, A. Full transmission and reflection of waves propagating through a maze of disorder. Phys. Rev. Lett. 113, 173901 (2014).

    Article  ADS  Google Scholar 

  11. Popoff, S. M., Goetschy, A., Liew, S. F., Stone, A. D. & Cao, H. Coherent control of total transmission of light through disordered media. Phys. Rev. Lett. 112, 133903 (2014).

    Article  ADS  Google Scholar 

  12. Davy, M., Shi, Z., Park, J., Tian, C. & Genack, A. Z. Universal structure of transmission eigenchannels inside opaque media. Nat. Commun. 6, 6893 (2015).

    Article  ADS  Google Scholar 

  13. Aubry, A. & Derode, A. Detection and imaging in a random medium: a matrix method to overcome multiple scattering and aberration. J. Appl. Phys. 106, 044903 (2009).

    Article  ADS  Google Scholar 

  14. Badon, A. et al. Smart optical coherence tomography for ultra-deep imaging through highly scattering media. Sci. Adv. 2, e1600370 (2016).

    Article  ADS  Google Scholar 

  15. Aubry, A., de Rosny, J., Minonzio, J.-G., Prada, C. & Fink, M. Gaussian beams and Legendre polynomials as invariants of the time reversal operator for a large rigid cylinder. J. Acoust. Soc. Am. 120, 2746 (2006).

    Article  ADS  Google Scholar 

  16. Robert, J.-L. & Fink, M. The prolate spheroidal wave functions as invariants of the time reversal operator for an extended scatterer in the Fraunhofer approximation. J. Acoust. Soc. Am. 125, 218 (2009).

    Article  ADS  Google Scholar 

  17. Yoon, S., Lee, H., Hong, J. H., Lim, Y.-S. & Choi, W. Laser scanning reflection-matrix microscopy for aberration-free imaging through intact mouse skull. Nat. Commun. 11, 5721 (2020).

    Article  ADS  Google Scholar 

  18. Jo, Y. et al. Through-skull brain imaging in vivo at visible wavelengths via dimensionality reduction adaptive-optical microscopy. Sci. Adv. 8, eabo4366 (2022).

    Article  Google Scholar 

  19. Lee, H. et al. High-throughput volumetric adaptive optical imaging using compressed time-reversal matrix. Light Sci. Appl. 11, 16 (2022).

    Article  ADS  Google Scholar 

  20. Weinberg, G., Sunray, E. & Katz, O. Noninvasive megapixel fluorescence microscopy through scattering layers by a virtual incoherent reflection matrix. Sci. Adv. 10, eadl5218 (2024).

    Article  ADS  Google Scholar 

  21. Badon, A. et al. Distortion matrix concept for deep optical imaging in scattering media. Sci. Adv. 6, eaay7170 (2020).

    Article  ADS  Google Scholar 

  22. Lambert, W., Cobus, L. A., Frappart, T., Fink, M. & Aubry, A. Distortion matrix approach for ultrasound imaging of random scattering media. Proc. Natl Acad. Sci. USA 117, 14645 (2020).

    Article  ADS  MathSciNet  Google Scholar 

  23. Bureau, F. et al. Three-dimensional ultrasound matrix imaging. Nat. Commun. 14, 6793 (2023).

    Article  ADS  Google Scholar 

  24. Murray, G. et al. Aberration free synthetic aperture second harmonic generation holography. Opt. Express 31, 32434 (2023).

    Article  ADS  Google Scholar 

  25. Giraudat, E. et al. Matrix imaging as a tool for high-resolution monitoring of deep volcanic plumbing systems with seismic noise. Commun. Earth Environ. 5, 509 (2024).

    Article  ADS  Google Scholar 

  26. Zhang, Y. et al. Adaptive optical multispectral matrix approach for label-free high-resolution imaging through complex scattering media. Adv. Photon. 7, 046008 (2025).

    Article  Google Scholar 

  27. Najar, U. et al. Harnessing forward multiple scattering for optical imaging deep inside an opaque medium. Nat. Commun. 15, 7349 (2024).

    Article  ADS  Google Scholar 

  28. Pai, P., Bosch, J., Kühmayer, M., Rotter, S. & Mosk, A. P. Scattering invariant modes of light in complex media. Nat. Photon. 15, 431 (2021).

    Article  ADS  Google Scholar 

  29. van den Wildenberg, S., Jia, X., Léopoldès, J. & Tourin, A. Ultrasonic tracking of a sinking ball in a vibrated dense granular suspension. Sci. Rep. 9, 5460 (2019).

    Article  ADS  Google Scholar 

  30. Montaldo, G., Tanter, M., Bercoff, J., Benech, N. & Fink, M. Coherent plane-wave compounding for very high frame rate ultrasonography and transient elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56, 489 (2009).

    Article  ADS  Google Scholar 

  31. Goïcoechea, A. et al. Reflection measurement of the scattering mean free path at the onset of multiple scattering. Phys. Rev. Lett. 133, 176301 (2024).

    Article  ADS  Google Scholar 

  32. Thomas, J.-L., Roux, P. & Fink, M. Inverse scattering analysis with an acoustic time-reversal mirror. Phys. Rev. Lett. 72, 637 (1994).

    Article  ADS  Google Scholar 

  33. Prada, C. & Fink, M. Separation of interfering acoustic scattered signals using the invariants of the time-reversal operator. Application to Lamb waves characterization. J. Acoust. Soc. Am. 104, 801 (1998).

    Article  ADS  Google Scholar 

  34. Gespa, N. & Überall, H. La Diffusion Acoustique par des Cibles Élastiques de Forme Géométrique Simple: Théories et Expériences (CEDOCAR, 1987).

  35. Quazi, A. An overview on the time delay estimate in active and passive systems for target localization. IEEE Trans. Acoust. Speech Signal Process. 29, 527 (1981).

    Article  Google Scholar 

  36. Desailly, Y., Pierre, J., Couture, O. & Tanter, M. Resolution limits of ultrafast ultrasound localization microscopy. Phys. Med. Biol. 60, 8723 (2015).

    Article  Google Scholar 

  37. Rüland, A. M. et al. Using a new marker clip system in breast cancer: Tumark Vision®clip – feasibility testing in everyday clinical practice. Breast Care 13, 114 (2018).

    Article  Google Scholar 

  38. Wijntjes, J. & van Alfen, N. Muscle ultrasound: present state and future opportunities. Muscle Nerve 63, 455 (2020).

    Article  Google Scholar 

  39. Papadacci, C. et al. Imaging the dynamics of cardiac fiber orientation in vivo using 3D ultrasound backscatter tensor imaging. Sci. Rep. 7, 830 (2017).

    Article  ADS  Google Scholar 

  40. Tseng, W. I., Dou, J., Reese, T. G. & Wedeen, V. J. Imaging myocardial fiber disarray and intramural strain hypokinesis in hypertrophic cardiomyopathy with MRI. J. Magn. Reson. Imaging 23, 1 (2005).

    Article  Google Scholar 

  41. Thompson, R. B. et al. Scattering of elastic waves in simple and complex polycrystals. Wave Motion 45, 655 (2008).

    Article  ADS  Google Scholar 

  42. Raoux, C., Chessel, A., Mahou, P., Latour, G. & Schanne-Klein, M.-C. Unveiling the lamellar structure of the human cornea over its full thickness using polarization-resolved SHG microscopy. Light Sci. Appl. 12, 190 (2023).

    Article  ADS  Google Scholar 

  43. Ammari, H. et al. Target identification using dictionary matching of generalized polarization tensors. Found. Comput. Math. 14, 27 (2013).

    Article  ADS  MathSciNet  Google Scholar 

  44. Ammari, H., Tran, M. P. & Wang, H. Shape identification and classification in echolocation. SIAM J. Imaging Sci. 7, 1883 (2014).

    Article  MathSciNet  MATH  Google Scholar 

  45. Xu, L., Li, J. & Stoica, P. Target detection and parameter estimation for MIMO radar systems. IEEE Trans. Aerosp. Electron. Syst. 44, 927 (2008).

    Article  ADS  Google Scholar 

  46. Pailhas, Y., Houssineau, J., Petillot, Y. R. & Clark, D. E. Tracking with MIMO sonar systems: applications to harbour surveillance. IET Radar Sonar Navig. 11, 629 (2017).

    Article  Google Scholar 

  47. De Jong, N., Bouakaz, A. & Frinking, P. Basic acoustic properties of microbubbles. Echocardiography 19, 229 (2002).

    Article  Google Scholar 

  48. Tremblay-Darveau, C., Williams, R. & Burns, P. N. Measuring absolute blood pressure using microbubbles. Ultrasound Med. Biol. 40, 775 (2014).

    Article  Google Scholar 

  49. Errico, C. et al. Ultrafast ultrasound localization microscopy for deep super-resolution vascular imaging. Nature 527, 499 (2015).

    Article  ADS  Google Scholar 

  50. Anker, J. N. et al. Biosensing with plasmonic nanosensors. Nat. Mater. 7, 442 (2008).

    Article  ADS  Google Scholar 

  51. Lambert, W., Cobus, L. A., Couade, M., Fink, M. & Aubry, A. Reflection matrix approach for quantitative imaging of scattering media. Phys. Rev. X 10, 021048 (2020).

    Google Scholar 

  52. Royer, D., Dieulesaint, E., Jia, X. & Shui, Y. Optical generation and detection of surface acoustic waves on a sphere. Appl. Phys. Lett. 52, 706 (1988).

    Article  ADS  Google Scholar 

  53. Clorennec, D. & Royer, D. Investigation of surface acoustic wave propagation on a sphere using laser ultrasonics. Appl. Phys. Lett. 85, 2435 (2004).

    Article  ADS  Google Scholar 

  54. Le Ber, A. et al. Fingerprint matrix imaging. Zenodo https://doi.org/10.5281/zenodo.14845779 (2024).

Download references

Acknowledgements

We thank Somatex Company for providing the lesion marker. We are grateful for the funding provided by the European Research Council under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No. 819261 under the REMINISCENCE project to A.A.). This project has also received funding from Labex WIFI (Laboratory of Excellence within the French Program Investments for the Future; Grant Nos ANR-10-LABX-24 and ANR-10-IDEX-0001-02 PSL* to M.F.) and from Agence Nationale de la Recherche (Grant No. ANR-22-ASTR-0020 under the AquaMat project to A.A.). L.M.R. was supported by the Austrian Science Fund (Project No. P32300-N27, WaveLand).

Author information

Author notes

  1. These authors contributed equally: Arthur Le Ber, Antton Goïcoechea.

Authors and Affiliations

  1. Institut Langevin, ESPCI Paris, PSL University, CNRS, Paris, France

    Arthur Le Ber, Antton Goïcoechea, Xiaoping Jia, Mathias Fink, Arnaud Tourin & Alexandre Aubry

  2. Institute for Theoretical Physics, Vienna University of Technology (TU Wien), Vienna, Austria

    Lukas M. Rachbauer & Stefan Rotter

  3. SuperSonic Imagine, Aix-en-Provence, France

    William Lambert

Authors
  1. Arthur Le Ber
    View author publications

    Search author on:PubMed Google Scholar

  2. Antton Goïcoechea
    View author publications

    Search author on:PubMed Google Scholar

  3. Lukas M. Rachbauer
    View author publications

    Search author on:PubMed Google Scholar

  4. William Lambert
    View author publications

    Search author on:PubMed Google Scholar

  5. Xiaoping Jia
    View author publications

    Search author on:PubMed Google Scholar

  6. Mathias Fink
    View author publications

    Search author on:PubMed Google Scholar

  7. Arnaud Tourin
    View author publications

    Search author on:PubMed Google Scholar

  8. Stefan Rotter
    View author publications

    Search author on:PubMed Google Scholar

  9. Alexandre Aubry
    View author publications

    Search author on:PubMed Google Scholar

Contributions

A.A. and S.R. initiated the project. A.A. supervised the project. A.L.B. and X.J. designed and performed the experiments on the granular medium. A.L.B. performed the lesion marker experiment and developed the postprocessing tools for the target detection experiment. W.L. performed the muscle tissue experiment. A.G. developed the postprocessing tools for the muscle tissue experiment. A.L.B., A.G., L.M.R., S.R. and A.A. developed the concept of the fingerprint operator and performed the theoretical study. A.L.B. and A.G. prepared the figures. A.L.B., A.G. and A.A. prepared the paper. All authors discussed the results and contributed to finalizing the paper.

Corresponding author

Correspondence to Alexandre Aubry.

Ethics declarations

Competing interests

A.L.B., A.G., L.M.R., W.L., X.J., M.F., A.T., S.R. and A.A. are inventors on a French patent related to this work held by SuperSonic Imagine and CNRS (no. FR2314789, filed December 2023). M.F. is cofounder of the SuperSonic Imagine company, which is commercializing one of the ultrasound platforms used in this study.

Peer review

Peer review information

Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Elastic target signatures encoded in the reference reflection matrix.

a, The reference reflection matrix R0 is measured on the target sphere placed in water. The confocal beamforming process applied to R0 selects not only the ballistic echo of the sphere but also its reverberations resulting from multiple reflections of bulk elastic waves (depicted by red arrows) at its inner surface. b, Matrix imaging decouples the input and output focal spots51, rin and rout, to highlight the contribution of circumferential waves (depicted by a black arrow) generated by the incoming wave at a specific angle of incidence with respect to sphere surface33. c, Cross-section of the focused reflection matrix, R0,xx(y, z), in the plane y = 0 and at depth z = 21 mm showing the diagonal contribution of the ballistic echo. d, Same matrix but at depth z = 28.5 mm showing the off-diagonal contribution of circumferential waves. e, (x, z)-section of the confocal image in the plane y = 0 showing the spatio-temporal dispersion of the target echo. f, Likelihood index map γ(r) (Eq. 2) built from the fingerprint operator indicating that we can accurately locate the target inside the reference environment (the sphere surface is highlighted by a red dashed line in panels e and f). Since in this case R ≡ R0(r0), this result serves as a consistency check for the formalism.

Extended Data Table 1 Experimental parameters
Full size table

Supplementary information

Supplementary Information

Supplementary Sections 1–8, Figs. 1–15 and Table 1.

Reporting Summary

Supplementary Video 1

Dynamic view of the confocal image in the bead experiment.

Supplementary Video 2

Likelihood 3D map of sphere 1 (in colour) superimposed to the confocal image (B&W) in a dynamic scenario where the target sinks inside the vibrated dense granular suspension.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Le Ber, A., Goïcoechea, A., Rachbauer, L.M. et al. Detection and characterization of targets in complex media using fingerprint matrices. Nat. Phys. (2025). https://doi.org/10.1038/s41567-025-03016-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1038/s41567-025-03016-2

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing