Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Parallelized telecom quantum networking with an ytterbium-171 atom array

Nature Physics (2025)Cite this article

Subjects

Abstract

The integration of quantum computers and sensors into a quantum network enables new capabilities in quantum information science. Most networks with atom-like qubits operate at visible or near-ultraviolet wavelengths and require conversion to the telecom band for long-distance communication, which reduces efficiency and potentially introduces noise. Here we report high-fidelity entanglement between ytterbium-171 atoms and optical photons generated directly in the telecommunication band, where fibre loss is low. The nuclear spin of the atom is entangled with a single photon in the time-bin basis, yielding a high atom-measurement-corrected atom–photon Bell state fidelity. This can be further improved by addressing photon measurement errors. By imaging the atom array onto an optical fibre array, we also implement a parallelized networking protocol that can increase the remote entanglement rate proportionately with the number of channels. We also preserve coherence on a memory qubit during operations on communication qubits. These results support the integration of atomic systems into scalable quantum networks.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Overview of the platform.
Fig. 2: Multilevel control of the ytterbium-171 array.
Fig. 3: Atom–photon entanglement.
Fig. 4: Parallelization with a fibre array.
Fig. 5: MCN.

Similar content being viewed by others

Data availability

The data that support the findings of this study are available from the corresponding authors upon request.

Code availability

The analysis codes related to this study are available from the corresponding authors upon request.

References

  1. Gisin, N., Ribordy, G., Tittel, W. & Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 74, 145–195 (2002).

    Article  MATH  ADS  Google Scholar 

  2. Pirandola, S. et al. Advances in quantum cryptography. Adv. Opt. Photon. 12, 1012 (2020).

    Article  Google Scholar 

  3. Gottesman, D., Jennewein, T. & Croke, S. Longer-baseline telescopes using quantum repeaters. Phys. Rev. Lett. 109, 070503 (2012).

    Article  ADS  Google Scholar 

  4. Malia, B. K., Wu, Y., Martínez-Rincón, J. & Kasevich, M. A. Distributed quantum sensing with mode-entangled spin-squeezed atomic states. Nature 612, 661–665 (2022).

    Article  ADS  Google Scholar 

  5. Kómár, P. et al. A quantum network of clocks. Nat. Phys. 10, 582–587 (2014).

    Article  Google Scholar 

  6. Nichol, B. C. et al. An elementary quantum network of entangled optical atomic clocks. Nature 609, 689–694 (2022).

    Article  ADS  Google Scholar 

  7. Wootters, W. K. & Zurek, W. H. A single quantum cannot be cloned. Nature 299, 802–803 (1982).

    Article  ADS  Google Scholar 

  8. Barz, S. et al. Demonstration of blind quantum computing. Science 335, 303–308 (2012).

    Article  MathSciNet  ADS  Google Scholar 

  9. Fitzsimons, J. F. Private quantum computation: an introduction to blind quantum computing and related protocols. npj Quantum Inf. 3, 23 (2017).

    Article  ADS  Google Scholar 

  10. Jiang, L., Taylor, J. M., Sørensen, A. S. & Lukin, M. D. Distributed quantum computation based on small quantum registers. Phys. Rev. A 76, 062323 (2007).

    Article  ADS  Google Scholar 

  11. Monroe, C. et al. Large-scale modular quantum-computer architecture with atomic memory and photonic interconnects. Phys. Rev. A 89, 022317 (2014).

    Article  ADS  Google Scholar 

  12. Stephenson, L. J. et al. High-rate, high-fidelity entanglement of qubits across an elementary quantum network. Phys. Rev. Lett. 124, 110501 (2020).

    Article  ADS  Google Scholar 

  13. Hensen, B. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).

    Article  ADS  Google Scholar 

  14. van Leent, T. et al. Entangling single atoms over 33 km telecom fibre. Nature 607, 69–73 (2022).

    Article  ADS  Google Scholar 

  15. Krutyanskiy, V. et al. Telecom-wavelength quantum repeater node based on a trapped-ion processor. Phys. Rev. Lett. 130, 213601 (2023).

    Article  ADS  Google Scholar 

  16. Uysal, M. T. et al. Spin-photon entanglement of a single Er3+ ion in the telecom band. Phys. Rev. X. 15, 011071 (2025).

    Google Scholar 

  17. Covey, J. P., Weinfurter, H. & Bernien, H. Quantum networks with neutral atom processing nodes. npj Quantum Inf. 9, 90 (2023).

    Article  ADS  Google Scholar 

  18. Moehring, D. L. et al. Entanglement of single-atom quantum bits at a distance. Nature 449, 68–71 (2007).

    Article  ADS  Google Scholar 

  19. Bernien, H. et al. Heralded entanglement between solid-state qubits separated by three metres. Nature 497, 86–90 (2013).

    Article  ADS  Google Scholar 

  20. Bhaskar, M. K. et al. Experimental demonstration of memory-enhanced quantum communication. Nature 580, 60–64 (2020).

    Article  ADS  Google Scholar 

  21. Ruskuc, A. et al. Multiplexed entanglement of multi-emitter quantum network nodes. Nature 639, 54–59 (2025).

    Article  Google Scholar 

  22. Stolk, A. et al. Telecom-band quantum interference of frequency-converted photons from remote detuned NV centers. PRX Quantum 3, 020359 (2022).

    Article  ADS  Google Scholar 

  23. Bersin, E. et al. Telecom networking with a diamond quantum memory. PRX Quantum 5, 010303 (2024).

    Article  ADS  Google Scholar 

  24. Zhong, T. et al. Nanophotonic rare-earth quantum memory with optically controlled retrieval. Science 357, 1392–1395 (2017).

    Article  MathSciNet  ADS  Google Scholar 

  25. Dibos, A. M., Raha, M., Phenicie, C. M. & Thompson, J. D. Atomic source of single photons in the telecom band. Phys. Rev. Lett. 120, 243601 (2018).

    Article  ADS  Google Scholar 

  26. Kindem, J. M. et al. Control and single-shot readout of an ion embedded in a nanophotonic cavity. Nature 580, 201–204 (2020).

    Article  ADS  Google Scholar 

  27. Hucul, D. et al. Modular entanglement of atomic qubits using photons and phonons. Nat. Phys. 11, 37–42 (2015).

    Article  Google Scholar 

  28. Huie, W., Menon, S. G., Bernien, H. & Covey, J. P. Multiplexed telecommunication-band quantum networking with atom arrays in optical cavities. Phys. Rev. Res. 3, 043154 (2021).

    Article  Google Scholar 

  29. Li, Y. & Thompson, J. D. High-rate and high-fidelity modular interconnects between neutral atom quantum processors. PRX Quantum 5, 020363 (2024).

    Article  Google Scholar 

  30. Canteri, M. et al. A photon-interfaced ten qubit quantum network node. Phys. Rev. Lett. 135, 080801 (2025).

    Article  Google Scholar 

  31. Hartung, L., Seubert, M., Welte, S., Distante, E. & Rempe, G. A quantum-network register assembled with optical tweezers in an optical cavity. Science 385, 179–183 (2024).

    Article  MathSciNet  Google Scholar 

  32. Trupke, M. et al. Atom detection and photon production in a scalable, open, optical microcavity. Phys. Rev. Lett. 99, 063601 (2007).

    Article  ADS  Google Scholar 

  33. Derntl, C. et al. Arrays of open, independently tunable microcavities. Opt. Express 22, 22111–22120 (2014).

    Article  ADS  Google Scholar 

  34. Menon, S. G., Glachman, N., Pompili, M., Dibos, A. & Bernien, H. An integrated atom array-nanophotonic chip platform with background-free imaging. Nat. Commun. 15, 6156 (2024).

    Article  Google Scholar 

  35. Shadmany, D. et al. Cavity QED in a high NA resonator. Sci. Adv. 11, eads8171 (2025).

    Article  Google Scholar 

  36. Sunami, S., Tamiya, S., Inoue, R., Yamasaki, H. & Goban, A. Scalable networking of neutral-atom qubits: nanofiber-based approach for multiprocessor fault-tolerant quantum computer. PRX Quantum 6, 010101 (2025).

    Article  Google Scholar 

  37. Huie, W. et al. Repetitive readout and real-time control of nuclear spin qubits in 171Yb atoms. PRX Quantum 4, 030337 (2023).

    Article  ADS  Google Scholar 

  38. Jenkins, A., Lis, J. W., Senoo, A., McGrew, W. F. & Kaufman, A. M. Ytterbium nuclear-spin qubits in an optical tweezer array. Phys. Rev. X 12, 021027 (2022).

    Google Scholar 

  39. Morigi, G., Eschner, J. & Keitel, C. H. Ground state laser cooling using electromagnetically induced transparency. Phys. Rev. Lett. 85, 4458–4461 (2000).

    Article  ADS  Google Scholar 

  40. Lis, J. W. et al. Midcircuit operations using the omg architecture in neutral atom arrays. Phys. Rev. X 13, 041035 (2023).

    Google Scholar 

  41. Barnes, K. et al. Assembly and coherent control of a register of nuclear spin qubits. Nat. Commun. 13, 2779 (2022).

    Article  ADS  Google Scholar 

  42. Chen, N. et al. Analyzing the Rydberg-based optical-metastable-ground architecture for 171Yb nuclear spins. Phys. Rev. A 105, 052438 (2022).

    Article  ADS  Google Scholar 

  43. Ma, S. et al. High-fidelity gates and mid-circuit erasure conversion in an atomic qubit. Nature 622, 279–284 (2023).

    Article  ADS  Google Scholar 

  44. Peper, M. et al. Spectroscopy and modeling of 171Yb Rydberg states for high-fidelity two-qubit gates. Phys. Rev. X 15, 011009 (2025).

    Google Scholar 

  45. Muniz, J. A. et al. High-fidelity universal gates in the 171Yb ground state nuclear spin qubit. PRX Quantum 6, 020334 (2025).

    Article  Google Scholar 

  46. Madjarov, I. S. et al. High-fidelity entanglement and detection of alkaline-earth Rydberg atoms. Nat. Phys. 16, 857–861 (2020).

    Article  Google Scholar 

  47. Li, L., Huie, W., Chen, N., DeMarco, B. & Covey, J. P. Active cancellation of servo-induced noise on stabilized lasers via feedforward. Phys. Rev. Appl. 18, 064005 (2022).

    Article  ADS  Google Scholar 

  48. Saha, S. et al. High-fidelity remote entanglement of trapped atoms mediated by time-bin photons. Nat. Commun. 16, 2533 (2025).

    Article  Google Scholar 

  49. Carolan, J. et al. Universal linear optics. Science 349, 711–716 (2015).

    Article  MathSciNet  Google Scholar 

  50. Pelucchi, E. et al. The potential and global outlook of integrated photonics for quantum technologies. Nat. Rev. Phys. 4, 194–208 (2021).

    Article  Google Scholar 

  51. Wollman, E. E. et al. Kilopixel array of superconducting nanowire single-photon detectors. Opt. Express 27, 35279–35289 (2019).

    Article  ADS  Google Scholar 

  52. Oripov, B. G. et al. A superconducting nanowire single-photon camera with 400,000 pixels. Nature 622, 730–734 (2023).

    Article  ADS  Google Scholar 

  53. Fleming, F. et al. High-efficiency, high-count-rate 2D superconducting nanowire single-photon detector array. Opt. Express 33, 27602–27614 (2025).

    Article  Google Scholar 

  54. Shaw, A. L. et al. Erasure cooling, control, and hyperentanglement of motion in optical tweezers. Science 388, 845–849 (2025).

    Article  MathSciNet  Google Scholar 

  55. Graham, T. M. et al. Mid-circuit measurements on a neutral atom quantum processor. Phys. Rev. X 13, 041051 (2023).

    Google Scholar 

  56. Singh, K. et al. Mid-circuit correction of correlated phase errors using an array of spectator qubits. Science 380, 1265–1269 (2023).

    Article  ADS  Google Scholar 

  57. Nakamura, Y. et al. A hybrid atom tweezer array of nuclear spin and optical clock qubits. Phys. Rev. X 14, 041062 (2024).

    Google Scholar 

  58. Norcia, M. A. et al. Midcircuit qubit measurement and rearrangement in a 171Yb atomic array. Phys. Rev. X 13, 041034 (2023).

    Google Scholar 

  59. Hu, B. et al. Site-selective cavity readout and classical error correction of a 5-bit atomic register. Phys. Rev. Lett. 134, 120801 (2025).

    Article  Google Scholar 

  60. Deist, E. et al. Mid-circuit cavity measurement in a neutral atom array. Phys. Rev. Lett. 129, 203602 (2022).

    Article  ADS  Google Scholar 

  61. Bluvstein, D. et al. Logical quantum processor based on reconfigurable atom arrays. Nature 626, 58–65 (2024).

  62. Tang, Z.-M., Yu, Y.-M. & Dong, C.-Z. Determination of static dipole polarizabilities of Yb atom. Chinese Phys. B 27, 063101 (2018).

    Article  ADS  Google Scholar 

  63. Endres, M. et al. Atom-by-atom assembly of defect-free one-dimensional cold atom arrays. Science 354, 1024–1027 (2016).

    Article  ADS  Google Scholar 

  64. Norcia, M. A. et al. Iterative assembly of 17Yb atom arrays with cavity-enhanced optical lattices. PRX Quantum 5, 030316 (2024).

    Article  Google Scholar 

  65. Gyger, F. et al. Continuous operation of large-scale atom arrays in optical lattices. Phys. Rev. Res. 6, 033104 (2024).

    Article  Google Scholar 

  66. Periwal, A. et al. Programmable interactions and emergent geometry in an array of atom clouds. Nature 600, 630–635 (2021).

    Article  ADS  Google Scholar 

  67. Peters, M. L. et al. Cavity-enabled real-time observation of individual atomic collisions. Preprint at https://arxiv.org/abs/2411.12622 (2024).

  68. Grinkemeyer, B. et al. Error-detected quantum operations with neutral atoms mediated by an optical cavity. Science 387, 1301–1305 (2025).

    Article  MathSciNet  Google Scholar 

  69. Graham, T. M. et al. Multi-qubit entanglement and algorithms on a neutral-atom quantum computer. Nature 604, 457–462 (2022).

    Article  ADS  Google Scholar 

  70. Pfister, C. et al. A universal test for gravitational decoherence. Nat. Commun. 7, 13022 (2016).

    Article  ADS  Google Scholar 

  71. Borregaard, J. & Pikovski, I. Testing quantum theory on curved space-time with quantum networks. Phys. Rev. Research 7, 023192 (2025).

    Article  Google Scholar 

  72. Covey, J. P., Pikovski, I. & Borregaard, J. Probing curved spacetime with a distributed atomic processor clock. PRX Quantum 6, 030310 (2025).

    Article  Google Scholar 

  73. Wcisło, P. et al. New bounds on dark matter coupling from a global network of optical atomic clocks. Sci. Adv. 4, eaau4869 (2018).

    Article  ADS  Google Scholar 

  74. Kennedy, C. J. et al. Precision metrology meets cosmology: improved constraints on ultralight dark matter from atom-cavity frequency comparisons. Phys. Rev. Lett. 125, 201302 (2020).

    Article  ADS  Google Scholar 

  75. Cho, J. W. et al. Optical repumping of triplet-P states enhances magneto-optical trapping of ytterbium atoms. Phys. Rev. A 85, 035401 (2012).

    Article  ADS  Google Scholar 

  76. Porsev, S. G., Rakhlina, Y. G. & Kozlov, M. G. Electric-dipole amplitudes, lifetimes, and polarizabilities of the low-lying levels of atomic ytterbium. Phys. Rev. A 60, 2781–2785 (1999).

    Article  ADS  Google Scholar 

  77. Scazza, F. Probing SU(N)-Symmetric Orbital Interactions with Ytterbium Fermi Gases in Optical Lattices. PhD thesis, LMU Munich (2015)

  78. Bettermann, O. Interorbital Interactions in Ytterbium-171. PhD thesis, LMU Munich (2022).

  79. Young, C. B. et al. An architecture for quantum networking of neutral atom processors. Appl. Phys. B 128, 151 (2022).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We acknowledge H. Bernien, J. Thompson, M. Saffman, E. Goldschmidt and B. DeMarco for stimulating discussions. We thank H. Bernien and A. Kaufman for critical reading of the manuscript. We also thank C. Anderson for generously sharing his SNSPD system. We acknowledge funding from the NSF QLCI for Hybrid Quantum Architectures and Networks (NSF award number 2016136); the NSF PHY Division (NSF award numbers 2112663 and 2339487); the NSF Quantum Interconnects Challenge for Transformational Advances in Quantum Systems (NSF award number 2137642); the ONR Young Investigator Program (ONR award number N00014-22-1-2311); the AFOSR Young Investigator Program (AFOSR award number FA9550-23-1-0059); and the US Department of Energy, Office of Science, National Quantum Information Science Research Centers.

Author information

Authors and Affiliations

  1. Department of Physics, The University of Illinois at Urbana-Champaign, Urbana, IL, USA

    Lintao Li, Xiye Hu, Zhubing Jia, William Huie, Won Kyu Calvin Sun,  Aakash, Yuhao Dong, Narisak Hiri-O-Tuppa & Jacob P. Covey

Authors
  1. Lintao Li
    View author publications

    Search author on:PubMed Google Scholar

  2. Xiye Hu
    View author publications

    Search author on:PubMed Google Scholar

  3. Zhubing Jia
    View author publications

    Search author on:PubMed Google Scholar

  4. William Huie
    View author publications

    Search author on:PubMed Google Scholar

  5. Won Kyu Calvin Sun
    View author publications

    Search author on:PubMed Google Scholar

  6. Aakash
    View author publications

    Search author on:PubMed Google Scholar

  7. Yuhao Dong
    View author publications

    Search author on:PubMed Google Scholar

  8. Narisak Hiri-O-Tuppa
    View author publications

    Search author on:PubMed Google Scholar

  9. Jacob P. Covey
    View author publications

    Search author on:PubMed Google Scholar

Contributions

L.L., X.H., Z.J. and J.P.C. envisioned this experiment. L.L., X.H. and Z.J. led this experiment and analysed the results. All authors contributed to the experimental techniques, the interpretation and analysis of data, and the vision for the parallelized networking architecture. W.H. performed the state preparation and measurement error correction analysis. W.K.C.S., A., Y.D. and N.H.-O.-T. performed the analysis of the optical cavity and contributed to those discussions in the paper. J.P.C. supervised this work, wrote the main text and directed the writing of the Supplementary Information.

Corresponding authors

Correspondence to Lintao Li or Jacob P. Covey.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Sebastian Eppelt and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

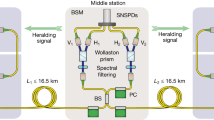
Extended Data Table 1 Error budget for entanglement generation and measurement
Full size table

Extended Data Fig. 1 Layout of the experiment.

The experiment is performed in a glass cell and the magnetic field is oriented vertically. Two microscope objectives are arranged horizontally. The first objective sends in the 760-nm optical tweezer array and collects the emitted telecom photons, and the second objective images the tweezer array for diagnostic purposes and performs fluorescence detection of the atoms. Optical pumping via 3P1 is performed with a horizontal beam (green) that has horizontal linear polarization37. Raman rotations of the metastable nuclear spin qubit are performed with a horizontal beam (blue) that has near-circular polarization. The clock beam (orange) and telecom beam (red) both propagate along the B-field axis with circular polarization. They propagate in opposite directions.

Extended Data Fig. 2 Measured photon arrival possibility, atom survival simulation, and atomic temperature versus number of attempts.

The blue histogram shows the summarized photon arrival versus attempt index of all the X-basis measurements. The orange curve shows the Monte Carlo simulation of the atom survival versus attempt index under same condition, showing good agreement between the exponential decay rates of the photon arrival probability and the expected atom survival. The green data shows atomic temperature after a number of entanglement attempts measured through release-recapture, solid line shows an exponential fit.

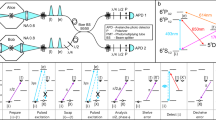
Extended Data Fig. 3 Experiment sequence for the attempt loop.

attempt_loop.pdf (a) Sub-dopper cooling. (b) State initialization to \(\left\vert {g}_{-}\right\rangle\). (c) Atomic X(Z)-basis measurement with (without) a Raman π/2 pulse before atomic state readout. (d) Atom-photon entanglement generation, a clock pulse transfer the atom from \(\left\vert {g}_{-}\right\rangle\) to \(\left\vert \uparrow \right\rangle\) at the start.

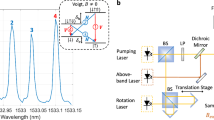
Extended Data Fig. 4 Magic conditions for metastable Raman transition.

(a) Simulated Raman π pulse fidelity under different single-photon Rabi frequencies and phase offsets between horizontal and vertical components. Here we set B = 120 G, Δ(3/2) = + 612 MHz. Within the contour we expect the π-pulse fidelity to exceed 99.9%. (b) The corresponding two-photon Raman Rabi frequency.

Extended Data Fig. 5 Atom-photon entanglement fidelity degradation from residual atom-motion entanglement.

(a) Illustration of the motion state evolution during REG sequence. The non-commutativity between eiΔk⋅x and \({e}^{-i{H}_{m}\Delta t}\) leads to non-overlapping motion wavefunctions associated to the early (blue) and late (red) time bin. (b) Fidelity degradation from radial and axial atom-motion entanglement as a function of time-bin separation. As our \(\Delta \overrightarrow{k}\) has components along both radial and axial directions, we calculate effects on the overall atom-photon Bell state fidelity from both axial and radial thermal states for different temperatures. The grey dashed line indicates Δt = 2.8μs which we use in our experimental sequence. We expect a ≈ 0.9% fidelity reduction from both radial and axial motion combined.

Extended Data Fig. 6 Time-delay interferometer (TDI).

An amplitude-modulating EOM directs single photons into either the free-space or the fiber-delay arm of the interferometer. The relative phase of the interferometer is locked continuously to a 1112-nm reference, and intermittently to a 1389-nm reference (see text for detail). A motor-driven fiber paddler maintains polarization stability in the fiber.

Extended Data Fig. 7 TDI visibility.

Pulse modulated 1389-nm CW light were sent through the same single-photon collection fiber into the short/long arm of the interferometer. A ramping voltage applied to the fast piezo actuator results in two interference fringes after the 50:50 BS, and are measured by two regular PDs in place of the SNSPDs, shown in red/blue. From the two fringes we extract an averaged visibility of 96.7(2)%.

Extended Data Fig. 8 Atom-photon entanglement infidelity and relative yield under different telecom Rabi frequencies and magnetic fields after post-selecting on receiving ≥1 1389-nm photons.

We find that using higher Rabi frequency and operating under higher B-field strength result in better atom-photon entanglement fidelities. Under a fixed B-field strength, there exist several local minima of atom-photon entanglement infidelity where the off-resonant transition from \(\left\vert \uparrow \right\rangle\) goes through multiples of 2Ï€. The star indicates the settings used our experiment.

Supplementary information

Supplementary Information

Supplementary Sections 1–3, Figs. 1–5 and Table 1.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, L., Hu, X., Jia, Z. et al. Parallelized telecom quantum networking with an ytterbium-171 atom array. Nat. Phys. (2025). https://doi.org/10.1038/s41567-025-03022-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1038/s41567-025-03022-4

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing