Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Universal anyon tunnelling in a chiral Luttinger liquid

Nature Physics (2025)Cite this article

Subjects

Abstract

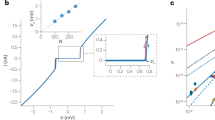
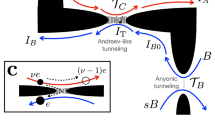
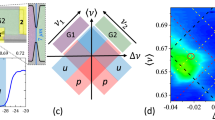
The edge modes of fractional quantum Hall liquids are described by chiral Luttinger liquid theory. Despite many years of experimental investigation, fractional quantum Hall edge modes are not fully understood, and clear discrepancies between experimental observations and detailed predictions of chiral Luttinger liquid theory remain. Here we report the measurements of tunnelling conductance between counterpropagating edge modes at a filling factor of 1/3 across a quantum point contact. We present evidence for the tunnelling of anyons through an incompressible liquid that exhibits universal scaling behaviour with respect to temperature, source–drain bias and barrier transmission, as originally proposed by prior theoretical work. For large transmission through the quantum point contact, we measured the tunnelling exponent \(\bar{g}=0.333\pm 0.005\) averaged over 29 independent datasets, consistent with the scaling dimension of 1/6 for a Laughlin quasiparticle at the edge. When combined with the measurements of the fractional charge and the recently observed anyonic statistical angle, the measured tunnelling exponent fully characterizes the topological order of the primary Laughlin state at the filling factor of 1/3.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Magnetotransport and QPC conductance at ν = 1 and ν = 1/3.
Fig. 2: Differential conductance at ν = 1/3 as a function of QPC transmission and temperature.
Fig. 3: Zero-bias tunnelling conductance versus T/T0.
Fig. 4: Scaling of reduced tunnelling conductance versus e*VSD/kBT.

Similar content being viewed by others

Data availability

Source data are provided with this paper. All other data that support the plots within this paper are available from the corresponding author upon reasonable request.

References

  1. Laughlin, R. B. Anomalous quantum Hall effect: an incompressible quantum fluid with fractionally charged excitations. Phys. Rev. Lett. 50, 1395–1398 (1983).

    Article  ADS  Google Scholar 

  2. Halperin, B. I. Statistics of quasiparticles and the hierarchy of fractional quantized Hall states. Phys. Rev. Lett. 52, 1583–1586 (1983).

    Article  ADS  Google Scholar 

  3. Arovas, D., Schrieffer, J. R. & Wilczek, F. Fractional statistics and the quantum Hall effect. Phys. Rev. Lett. 53, 722–723 (1984).

    Article  ADS  Google Scholar 

  4. Wen, X. G. Chiral Luttinger liquid and the edge excitations in the fractional quantum Hall states. Phys. Rev. B 41, 12838–12844 (1990).

    Article  ADS  Google Scholar 

  5. Wen, X. G. Edge transport properties of the fractional quantum Hall states and weak-impurity scattering of a one-dimensional charge-density wave. Phys. Rev. B 44, 5708–5719 (1991).

    Article  ADS  Google Scholar 

  6. Wen, X. G. Topological orders and edge excitations in fractional quantum Hall states. Adv. Phys. 44, 405–473 (1995).

    Article  ADS  Google Scholar 

  7. Kane, C. L. & Fisher, M. P. A. Transport in a one-channel Luttinger liquid. Phys. Rev. Lett. 68, 1220–1223 (1992).

    Article  ADS  Google Scholar 

  8. Kane, C. L. & Fisher, M. P. A. Transmission through barriers and resonant tunneling in an interacting one-dimensional electron gas. Phys. Rev. B 46, 15233–15262 (1992).

    Article  ADS  Google Scholar 

  9. Kane, C. L. & Fisher, M. P. A. Nonequilibrium noise and fractional charge in the quantum Hall effect. Phys. Rev. Lett. 72, 724–727 (1994).

    Article  ADS  Google Scholar 

  10. Fendley, P., Saleur, H. & Warner, N. Exact solution of a massless scalar field with a relevant boundary interaction. Nucl. Phys. B 430, 577–596 (1994).

    Article  ADS  MathSciNet  Google Scholar 

  11. Fendley, P., Ludwig, A. W. W. & Saleur, H. Exact conductance through point contacts in the ν = 1/3 fractional quantum Hall effect. Phys. Rev. Lett. 74, 3005–3008 (1995).

    Article  ADS  Google Scholar 

  12. Fendley, P., Ludwig, A. W. W. & Saleur, H. Exact nonequilibrium transport through point contacts in quantum wires and fractional quantum Hall devices. Phys. Rev. B 52, 8934–8950 (1995).

    Article  ADS  Google Scholar 

  13. Chamon, C. D. C. & Wen, X. G. Resonant tunneling in the fractional quantum Hall regime. Phys. Rev. Lett. 70, 2605–2608 (1993).

    Article  ADS  Google Scholar 

  14. Chamon, C. D. C., Freed, D. E. & Wen, X. G. Tunneling and quantum noise in one-dimensional Luttinger liquids. Phys. Rev. B 51, 2363–2379 (1995).

    Article  ADS  Google Scholar 

  15. de Picciotto, R. et al. Direct observation of a fractional charge. Nature 389, 162–164 (1997).

    Article  ADS  Google Scholar 

  16. Saminadayar, L., Glattli, D. C., Jin, Y. & Etienne, B. Observation of the e/3 fractionally charged Laughlin quasiparticle. Phys. Rev. Lett. 79, 2526–2529 (1997).

    Article  ADS  Google Scholar 

  17. Nakamura, J., Liang, S., Gardner, G. C. & Manfra, M. J. Direct observation of anyonic braiding statistics. Nat. Phys. 16, 931–936 (2020).

    Article  Google Scholar 

  18. Nakamura, J., Liang, S., Gardner, G. C. & Manfra, M. J. Impact of bulk-edge coupling on observation of anyonic braiding statistics in quantum Hall interferometers. Nat. Commun. 13, 344 (2022).

  19. Nakamura, J., Liang, S., Gardner, G. C. & Manfra, M. J. Fabry-Pérot interferometry at the ν = 2/5 fractional quantum Hall state. Phys. Rev. X 13, 041012 (2023).

    Google Scholar 

  20. Bartolomei, H. et al. Fractional statistics in anyon collisions. Science 368, 173–177 (2020).

    Article  ADS  MathSciNet  Google Scholar 

  21. Ruelle, M. et al. Comparing fractional quantum Hall Laughlin and Jain topological orders with the anyon collider. Phys. Rev. X 13, 011031 (2023).

    Google Scholar 

  22. Lee, J. Y. M. et al. Partitioning of diluted anyons reveals their braiding statistics. Nature 617, 277–281 (2023).

    Article  ADS  Google Scholar 

  23. Milliken, F., Umbach, C. & Webb, R. Indications of a Luttinger liquid in the fractional quantum Hall regime. Solid State Commun. 97, 309–313 (1996).

    Article  ADS  Google Scholar 

  24. Chang, A. M., Pfeiffer, L. N. & West, K. W. Observation of chiral Luttinger behavior in electron tunneling into fractional quantum Hall edges. Phys. Rev. Lett. 77, 2538–2541 (1996).

    Article  ADS  Google Scholar 

  25. Grayson, M., Tsui, D. C., Pfeiffer, L. N., West, K. W. & Chang, A. M. Continuum of chiral Luttinger liquids at the fractional quantum Hall edge. Phys. Rev. Lett. 80, 1062–1065 (1998).

    Article  ADS  Google Scholar 

  26. Chang, A. M., Wu, M. K., Chi, C. C., Pfeiffer, L. N. & West, K. W. Plateau behavior in the chiral Luttinger liquid exponent. Phys. Rev. Lett. 86, 143–146 (2001).

    Article  ADS  Google Scholar 

  27. Goldman, V. J. & Su, B. Resonant tunneling in the quantum Hall regime: measurement of fractional charge. Science 267, 1010–1012 (1995).

    Article  ADS  Google Scholar 

  28. Maasilta, I. & Goldman, V. Line shape of resonant tunneling between fractional quantum Hall edges. Phys. Rev. B 55, 4081 (1997).

    Article  ADS  Google Scholar 

  29. Roddaro, S. et al. Nonlinear quasiparticle tunneling between fractional quantum Hall edges. Phys. Rev. Lett. 90, 046805 (2003).

    Article  ADS  Google Scholar 

  30. Roddaro, S., Pellegrini, V., Beltram, F., Biasiol, G. & Sorba, L. Interedge strong-to-weak scattering evolution at a constriction in the fractional quantum Hall regime. Phys. Rev. Lett. 93, 046801 (2004).

    Article  ADS  Google Scholar 

  31. Roddaro, S., Pellegrini, V. & Beltram, F. Quasi-particle tunneling at a constriction in a fractional quantum Hall state. Solid State Commun. 131, 565–572 (2004).

    Article  ADS  Google Scholar 

  32. Baer, S. et al. Experimental probe of topological orders and edge excitations in the second Landau level. Phys. Rev. B 90, 075403 (2014).

    Article  ADS  Google Scholar 

  33. Hennel, S. et al. Quasiparticle tunneling in the lowest Landau level. Phys. Rev. B 97, 245305 (2018).

    Article  ADS  Google Scholar 

  34. Miller, J. B. et al. Fractional quantum Hall effect in a quantum point contact at filling fraction 5/2. Nat. Phys. 3, 561–565 (2007).

    Article  Google Scholar 

  35. Radu, I. P. et al. Quasi-particle properties from tunneling in the ν = 5/2 fractional quantum Hall state. Science 320, 899–902 (2008).

    Article  ADS  Google Scholar 

  36. Veillon, A. et al. Observation of the scaling dimension of fractional quantum Hall anyons. Nature 632, 517–521 (2024).

    Article  ADS  Google Scholar 

  37. Snizhko, K. & Cheianov, V. Scaling dimension of quantum Hall quasiparticles from tunneling-current noise measurements. Phys. Rev. B 91, 195151 (2015).

    Article  ADS  Google Scholar 

  38. Schiller, N., Oreg, Y. & Snizhko, K. Extracting the scaling dimension of quantum Hall quasiparticles from current correlations. Phys. Rev. B 105, 165150 (2022).

    Article  ADS  Google Scholar 

  39. Cohen, L. A. et al. Universal chiral Luttinger liquid behavior in a graphene fractional quantum Hall point contact. Science 382, 542–547 (2023).

    Article  ADS  Google Scholar 

  40. Chamon, C. D. C. & Wen, X. G. Sharp and smooth boundaries of quantum Hall liquids. Phys. Rev. B 49, 8227–8241 (1994).

    Article  ADS  Google Scholar 

  41. Chamon, C. D. C., Freed, D. E., Kivelson, S. A., Sondhi, S. L. & Wen, X. G. Two point-contact interferometer for quantum Hall systems. Phys. Rev. B 55, 2331–2343 (1997).

    Article  ADS  Google Scholar 

  42. Nakamura, J. et al. Aharonov-Bohm interference of fractional quantum Hall edge modes. Nat. Phys. 15, 563–569 (2019).

    Article  Google Scholar 

  43. Liang, S., Nakamura, J., Gardner, G. C. & Manfra, M. J. Single electron interference and capacitive edge mode coupling generates Φ0/2 flux periodicity in Fabry-Pérot interferometers. Nat. Commun. 16, 7586 (2025).

  44. Bhattacharyya, R., Banerjee, M., Heiblum, M., Mahalu, D. & Umansky, V. Melting of interference in the fractional quantum Hall effect: appearance of neutral modes. Phys. Rev. Lett. 122, 246801 (2019).

    Article  ADS  Google Scholar 

  45. Schiller, N. et al. Scaling tunnelling noise in the fractional quantum Hall effect tells about renormalization and breakdown of chiral Luttinger liquid. Preprint at https://arxiv.org/abs/2403.17097 (2024).

  46. Eisenstein, J., Pfeiffer, L. & West, K. Independently contacted two-dimensional electron systems in double quantum wells. Appl. Phys. Lett. 57, 2324–2326 (1990).

    Article  ADS  Google Scholar 

  47. Rosenow, B. & Halperin, B. I. Nonuniversal behavior of scattering between fractional quantum Hall edges. Phys. Rev. Lett. 88, 096404 (2002).

    Article  ADS  Google Scholar 

  48. Papa, E. & MacDonald, A. H. Interactions suppress quasiparticle tunneling at Hall bar constrictions. Phys. Rev. Lett. 93, 126801 (2004).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

These experiments are sponsored by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, under award number DE-SC0020138. The theoretical work is sponsored by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, under award number DE-FG02-06ER46316. The content of the information presented here does not necessarily reflect the position or the policy of the US government, and no official endorsement should be inferred.

Author information

Authors and Affiliations

  1. Department of Physics and Astronomy, Purdue University, West Lafayette, IN, USA

    Ramon Guerrero-Suarez, Adithya Suresh, Tanmay Maiti, Shuang Liang, James Nakamura & Michael Manfra

  2. Microsoft Quantum Lab West Lafayette, West Lafayette, IN, USA

    Geoffrey Gardner & Michael Manfra

  3. Department of Physics, Boston University, Boston, MA, USA

    Claudio Chamon

  4. Elmore Family School of Electrical and Computer Engineering, Purdue University, West Lafayette, IN, USA

    Michael Manfra

  5. School of Materials Engineering, Purdue University, West Lafayette, IN, USA

    Michael Manfra

Authors
  1. Ramon Guerrero-Suarez
    View author publications

    Search author on:PubMed Google Scholar

  2. Adithya Suresh
    View author publications

    Search author on:PubMed Google Scholar

  3. Tanmay Maiti
    View author publications

    Search author on:PubMed Google Scholar

  4. Shuang Liang
    View author publications

    Search author on:PubMed Google Scholar

  5. James Nakamura
    View author publications

    Search author on:PubMed Google Scholar

  6. Geoffrey Gardner
    View author publications

    Search author on:PubMed Google Scholar

  7. Claudio Chamon
    View author publications

    Search author on:PubMed Google Scholar

  8. Michael Manfra
    View author publications

    Search author on:PubMed Google Scholar

Contributions

R.G.-S., A.S. and M.M. designed the experiments. J.N. and M.M. designed the heterostructure. S.L. and G.G. conducted the molecular-beam epitaxy growth. J.N. fabricated the devices. R.G.-S. and A.S. performed the measurements and analysed the data with input from T.M. and M.M. C.C. provided theoretical support. R.G.-S., A.S., C.C. and M.M. wrote the paper with input from all authors.

Corresponding author

Correspondence to Michael Manfra.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figs. 1–6, equations (1)–(3) and Discussion.

Source data

Source Data Fig. 1

Measurement source data.

Source Data Fig. 2

Measurement source data.

Source Data Fig. 3

Theoretical curve data and measurement source data.

Source Data Fig. 4

Extracted data from the least squares fit.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Guerrero-Suarez, R., Suresh, A., Maiti, T. et al. Universal anyon tunnelling in a chiral Luttinger liquid. Nat. Phys. (2025). https://doi.org/10.1038/s41567-025-03039-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1038/s41567-025-03039-9

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing