Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Statistical localization of U(1) lattice gauge theory in a Rydberg simulator

Nature Physics (2026)Cite this article

Subjects

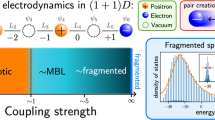
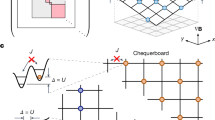
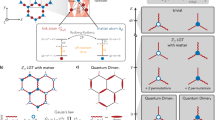
Abstract

Lattice gauge theories provide a framework for describing dynamical systems ranging from nuclei to materials. When they host concatenated conservation laws, their Hilbert space can fragment into subspaces labelled by non-local quantities—a phenomenon known as Hilbert space fragmentation. Although non-local conservation laws are expected not to hinder local thermalization, this assumption has been questioned by the idea of statistical localization, where motifs of microscopic configurations remain frozen owing to strong fragmentation. Here we observe experimental signatures of such behaviour in a constrained lattice gauge theory using a facilitated Rydberg-atom array, where atoms mediate the dynamics of charge clusters whose non-local net-charge patterns remain invariant. By reconstructing observables sampled over time, we probe the spatial distribution of conserved quantities. We find that strong Hilbert space fragmentation keeps these quantities locally distributed in typical quantum states, even though they are defined by non-local string-like operators. This establishes a setting for high-energy studies of cluster dynamics and low-energy investigations of strong zero modes that persist in infinite-temperature topological systems.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Emergence of statistical localization from charge cluster conservation in a constrained U(1) LGT.
Fig. 2: Experimental studies of ergodicity breaking.
Fig. 3: State-dependent localization.
Fig. 4: Experimental observation of statistical localization.

Similar content being viewed by others

Data availability

The data presented in this manuscript are available via Zenodo at https://doi.org/10.5281/zenodo.18012627 (ref. 77) and from the corresponding author upon reasonable request.

References

  1. Kogut, J. B. The lattice gauge theory approach to quantum chromodynamics. Rev. Mod. Phys. 55, 775 (1983).

    Article  ADS  Google Scholar 

  2. Greensite, J. The confinement problem in lattice gauge theory. Prog. Part. Nucl. Phys. 51, 1–83 (2003).

    Article  ADS  Google Scholar 

  3. Sachdev, S. Emergent gauge fields and the high-temperature superconductors. Philos. Trans. A 374, 20150248 (2016).

    ADS  Google Scholar 

  4. Scherg, S. et al. Observing non-ergodicity due to kinetic constraints in tilted Fermi–Hubbard chains. Nat. Commun. 12, 4490 (2021).

    Article  ADS  Google Scholar 

  5. Kohlert, T. et al. Exploring the regime of fragmentation in strongly tilted Fermi–Hubbard chains. Phys. Rev. Lett. 130, 010201 (2023).

    Article  ADS  Google Scholar 

  6. Adler, D. et al. Observation of Hilbert space fragmentation and fractonic excitations in 2D. Nature 636, 80 (2024).

    Article  ADS  Google Scholar 

  7. Kim, K., Yang, F., Mølmer, K. & Ahn, J. Realization of an extremely anisotropic Heisenberg magnet in Rydberg atom arrays. Phys. Rev. X 14, 011025 (2024).

    Google Scholar 

  8. Zhao, L., Datla, P. R., Tian, W., Aliyu, M. M. & Loh, H. Observation of quantum thermalization restricted to Hilbert space fragments and \({{\mathbb{Z}}}_{2k}\) scars. Phys. Rev. X 15, 011035 (2025).

  9. Honda, K. et al. Observation of slow relaxation due to Hilbert space fragmentation in strongly interacting Bose–Hubbard chains. Sci. Adv. 11, eadv3255 (2025).

    Article  ADS  Google Scholar 

  10. Gonzalez-Cuadra, D. et al. Observation of string breaking on a (2 + 1)D Rydberg quantum simulator. Nature 642, 321–326 (2025).

    Article  ADS  Google Scholar 

  11. Tagliacozzo, L., Celi, A., Orland, P. & Lewenstein, M. Simulations of non-Abelian gauge theories with optical lattices. Nat. Commun. 4, 2615 (2013).

    Article  ADS  Google Scholar 

  12. Banerjee, D. et al. Atomic quantum simulation of dynamical gauge fields coupled to Fermionic matter: from string breaking to evolution after a quench. Phys. Rev. Lett. 109, 175302 (2012).

    Article  ADS  Google Scholar 

  13. Bañuls, M. C. et al. Simulating lattice gauge theories within quantum technologies. Eur. Phys. J. D 74, 165 (2020).

    Article  ADS  Google Scholar 

  14. Zohar, E., Cirac, J. I. & Reznik, B. Cold-atom quantum simulator for SU(2) Yang–Mills lattice gauge theory. Phys. Rev. Lett. 110, 125304 (2013).

    Article  ADS  Google Scholar 

  15. Schweizer, C. et al. Floquet approach to \({{\mathbb{Z}}}_{2}\) lattice gauge theories with ultracold atoms in optical lattices. Nat. Phys. 15, 1168–1173 (2019).

  16. Zhou, Z.-Y. et al. Thermalization dynamics of a gauge theory on a quantum simulator. Science 377, 311–314 (2022).

    Article  ADS  MathSciNet  Google Scholar 

  17. Halimeh, J. C., Aidelsburger, M., Grusdt, F., Hauke, P. & Yang, B. Cold-atom quantum simulators of gauge theories. Nat. Phys. 21, 25–36 (2025).

    Article  Google Scholar 

  18. Surace, F. M. et al. Lattice gauge theories and string dynamics in Rydberg atom quantum simulators. Phys. Rev. X 10, 021041 (2020).

    Google Scholar 

  19. Bauer, C. W., Davoudi, Z., Klco, N. & Savage, M. J. Quantum simulation of fundamental particles and forces. Nat. Rev. Phys. 5, 420–432 (2023).

    Article  Google Scholar 

  20. Nandkishore, R. & Huse, D. A. Many-body localization and thermalization in quantum statistical mechanics. Annu. Rev. Condens. Matter Phys. 6, 15–38 (2015).

    Article  ADS  Google Scholar 

  21. Schreiber, M. et al. Observation of many-body localization of interacting fermions in a quasirandom optical lattice. Science 349, 842–845 (2015).

    Article  ADS  MathSciNet  Google Scholar 

  22. Bernien, H. et al. Probing many-body dynamics on a 51-atom quantum simulator. Nature 551, 579–584 (2017).

    Article  ADS  Google Scholar 

  23. Turner, C. J., Michailidis, A. A., Abanin, D. A., Serbyn, M. & Papić, Z. Weak ergodicity breaking from quantum many-body scars. Nat. Phys. 14, 745–749 (2018).

    Article  Google Scholar 

  24. Smith, A., Knolle, J., Moessner, R. & Kovrizhin, D. L. Dynamical localization in \({{\mathbb{Z}}}_{2}\) lattice gauge theories. Phys. Rev. B 97, 245137 (2018).

  25. Karpov, P., Verdel, R., Huang, Y.-P., Schmitt, M. & Heyl, M. Disorder-free localization in an interacting 2D lattice gauge theory. Phys. Rev. Lett. 126, 130401 (2021).

    Article  ADS  Google Scholar 

  26. Banerjee, D. & Sen, A. Quantum scars from zero modes in an Abelian lattice gauge theory on ladders. Phys. Rev. Lett. 126, 220601 (2021).

    Article  ADS  MathSciNet  Google Scholar 

  27. Aramthottil, A. S. et al. Scar states in deconfined \({{\mathbb{Z}}}_{2}\) lattice gauge theories. Phys. Rev. B 106, L041101 (2022).

  28. Halimeh, J. C., Barbiero, L., Hauke, P., Grusdt, F. & Bohrdt, A. Robust quantum many-body scars in lattice gauge theories. Quantum 7, 1004 (2023).

    Article  Google Scholar 

  29. Desaules, J.-Y. et al. Weak ergodicity breaking in the Schwinger model. Phys. Rev. B 107, L201105 (2023).

    Article  ADS  Google Scholar 

  30. Desaules, J.-Y. et al. Prominent quantum many-body scars in a truncated Schwinger model. Phys. Rev. B 107, 205112 (2023).

    Article  ADS  Google Scholar 

  31. Gyawali, G. et al. Observation of disorder-free localization and efficient disorder averaging on a quantum processor. Preprint at https://arxiv.org/abs/2410.06557 (2024).

  32. Morong, W. et al. Observation of Stark many-body localization without disorder. Nature 599, 393–398 (2021).

    Article  ADS  Google Scholar 

  33. Sala, P., Rakovszky, T., Verresen, R., Knap, M. & Pollmann, F. Ergodicity breaking arising from Hilbert space fragmentation in dipole-conserving Hamiltonians. Phys. Rev. X 10, 011047 (2020).

    Google Scholar 

  34. Khemani, V., Hermele, M. & Nandkishore, R. Localization from Hilbert space shattering: From theory to physical realizations. Phys. Rev. B 101, 174204 (2020).

    Article  ADS  Google Scholar 

  35. Yang, Z.-C., Liu, F., Gorshkov, A. V. & Iadecola, T. Hilbert-space fragmentation from strict confinement. Phys. Rev. Lett. 124, 207602 (2020).

    Article  ADS  Google Scholar 

  36. Jeyaretnam, J., Bhore, T., Osborne, J. J., Halimeh, J. C. & Papić, Z. Hilbert space fragmentation at the origin of disorder-free localization in the lattice Schwinger model. Commun. Phys. 8, 172 (2025).

  37. Desaules, J.-Y. et al. Ergodicity breaking under confinement in cold-atom quantum simulators. Quantum 8, 1274 (2024).

    Article  Google Scholar 

  38. Ciavarella, A. N., Bauer, C. W. & Halimeh, J. C. Generic Hilbert space fragmentation in Kogut–Susskind lattice gauge theories. Phys. Rev. D 112, L091501 (2025).

    Article  ADS  MathSciNet  Google Scholar 

  39. Wang, Y.-Y. et al. Exploring Hilbert-space fragmentation on a superconducting processor. PRX Quantum 6, 010325 (2025).

    Article  ADS  Google Scholar 

  40. Karch, S. et al. Probing quantum many-body dynamics using subsystem Loschmidt echos. Preprint at https://arxiv.org/abs/2501.16995 (2025).

  41. Moudgalya, S., Bernevig, B. A. & Regnault, N. Quantum many-body scars and Hilbert space fragmentation: a review of exact results. Rep. Prog. Phys. 85, 086501 (2022).

    Article  ADS  MathSciNet  Google Scholar 

  42. Deutsch, J. M. Quantum statistical mechanics in a closed system. Phys. Rev. A 43, 2046 (1991).

    Article  ADS  Google Scholar 

  43. Rigol, M., Dunjko, V. & Olshanii, M. Thermalization and its mechanism for generic isolated quantum systems. Nature 452, 854–858 (2008).

    Article  ADS  Google Scholar 

  44. Rakovszky, T., Sala, P., Verresen, R., Knap, M. & Pollmann, F. Statistical localization: from strong fragmentation to strong edge modes. Phys. Rev. B 101, 125126 (2020).

    Article  ADS  Google Scholar 

  45. Chandran, A., Kim, I. H., Vidal, G. & Abanin, D. A. Constructing local integrals of motion in the many-body localized phase. Phys. Rev. B 91, 085425 (2015).

    Article  ADS  Google Scholar 

  46. Imbrie, J. Z., Ros, V. & Scardicchio, A. Local integrals of motion in many-body localized systems. Ann. Phys. (Berlin) 529, 1600278 (2017).

    Article  ADS  MathSciNet  Google Scholar 

  47. Rademaker, L., Ortuño, M. & Somoza, A. M. Many-body localization from the perspective of integrals of motion. Ann. Phys. 529, 1600322 (2017).

    Article  Google Scholar 

  48. Singh, H., Ware, B., Vasseur, R. & Gopalakrishnan, S. Local integrals of motion and the quasiperiodic many-body localization transition. Phys. Rev. B 103, L220201 (2021).

    Article  ADS  Google Scholar 

  49. Ros, V., Müller, M. & Scardicchio, A. Integrals of motion in the many-body localized phase. Nucl. Phys. B 891, 420–465 (2015).

    Article  ADS  MathSciNet  Google Scholar 

  50. Bertoni, C., Eisert, J., Kshetrimayum, A., Nietner, A. & Thomson, S. Local integrals of motion and the stability of many-body localization in Wannier-Stark potentials. Phys. Rev. B 109, 024206 (2024).

    Article  ADS  Google Scholar 

  51. Wahl, T. B. & Béri, B. Local integrals of motion for topologically ordered many-body localized systems. Phys. Rev. Res. 2, 033099 (2020).

    Article  Google Scholar 

  52. Marcuzzi, M. et al. Facilitation dynamics and localization phenomena in Rydberg lattice gases with position disorder. Phys. Rev. Lett. 118, 063606 (2017).

    Article  ADS  Google Scholar 

  53. Magoni, M., Mazza, P. P. & Lesanovsky, I. Emergent Bloch oscillations in a kinetically constrained Rydberg spin lattice. Phys. Rev. Lett. 126, 103002 (2021).

    Article  ADS  MathSciNet  Google Scholar 

  54. Hart, O. Exact Mazur bounds in the pair-flip model and beyond. SciPost Phys. 7, 040 (2024).

    Article  Google Scholar 

  55. Hahn, D., McClarty, P. A. & Luitz, D. J. Information dynamics in a model with Hilbert space fragmentation. SciPost Phys. 11, 074 (2021).

    Article  ADS  MathSciNet  Google Scholar 

  56. Choi, J. et al. Preparing random states and benchmarking with many-body quantum chaos. Nature 613, 468–473 (2023).

    Article  ADS  Google Scholar 

  57. Pilatowsky-Cameo, S., Dag, C. B., Ho, W. W. & Choi, S. Complete Hilbert-space ergodicity in quantum dynamics of generalized Fibonacci drives. Phys. Rev. Lett. 131, 250401 (2023).

    Article  ADS  MathSciNet  Google Scholar 

  58. Pilatowsky-Cameo, S., Marvian, I., Choi, S. & Ho, W. W. Hilbert-space ergodicity in driven quantum systems: obstructions and designs. Phys. Rev. X 14, 041059 (2024).

    Google Scholar 

  59. Ghosh, S., Langlett, C. M., Hunter-Jones, N. & Rodriguez-Nieva, J. F. Late-time ensembles of quantum states in quantum chaotic systems. Phys. Rev. B 112, 094302 (2025).

    Article  ADS  Google Scholar 

  60. Le, Y., Zhang, Y., Gopalakrishnan, S., Rigol, M. & Weiss, D. S. Observation of hydrodynamization and local prethermalization in 1D Bose gases. Nature 618, 494–499 (2023).

    Article  ADS  Google Scholar 

  61. Fendley, P. Strong zero modes and eigenstate phase transitions in the XYZ/interacting Majorana chain. J. Phys. A 49, 30LT01 (2016).

    Article  MathSciNet  Google Scholar 

  62. Olund, C. T., Yao, N. Y. & Kemp, J. Boundary strong zero modes. Phys. Rev. B 111, L201114 (2025).

    Article  ADS  Google Scholar 

  63. Else, D. V., Fendley, P., Kemp, J. & Nayak, C. Prethermal strong zero modes and topological qubits. Phys. Rev. X 7, 041062 (2017).

    Google Scholar 

  64. Kempkes, S. et al. Robust zero-energy modes in an electronic higher-order topological insulator. Nat. Mater. 18, 1292–1297 (2019).

    Article  ADS  Google Scholar 

  65. Verresen, R., Jones, N. G. & Pollmann, F. Topology and edge modes in quantum critical chains. Phys. Rev. Lett. 120, 057001 (2018).

    Article  ADS  Google Scholar 

  66. Verresen, R., Thorngren, R., Jones, N. G. & Pollmann, F. Gapless topological phases and symmetry-enriched quantum criticality. Phys. Rev. X 11, 041059 (2021).

    Google Scholar 

  67. Morningstar, A., Khemani, V. & Huse, D. A. Kinetically constrained freezing transition in a dipole-conserving system. Phys. Rev. B 101, 214205 (2020).

    Article  ADS  Google Scholar 

  68. Wang, C. & Yang, Z.-C. Freezing transition in the particle-conserving East model. Phys. Rev. B 108, 144308 (2023).

    Article  ADS  Google Scholar 

  69. Pozderac, C., Speck, S., Feng, X., Huse, D. A. & Skinner, B. Exact solution for the filling-induced thermalization transition in a one-dimensional fracton system. Phys. Rev. B 107, 045137 (2023).

    Article  ADS  Google Scholar 

  70. Classen-Howes, J., Senese, R. & Prakash, A. Universal freezing transitions of dipole-conserving chains. Phys. Rev. B 112, 125148 (2025).

    Article  ADS  Google Scholar 

  71. Tian, W. et al. Parallel assembly of arbitrary defect-free atom arrays with a multitweezer algorithm. Phys. Rev. Applied 19, 034048 (2023).

    Article  ADS  Google Scholar 

  72. Labuhn, H. et al. Single-atom addressing in microtraps for quantum-state engineering using Rydberg atoms. Phys. Rev. A 90, 023415 (2014).

    Article  ADS  Google Scholar 

  73. Yang, F., Yarloo, H., Zhang, H.-C., Mølmer, K. & Nielsen, A. E. Probing Hilbert space fragmentation with strongly interacting Rydberg atoms. Phys. Rev. B 111, 144313 (2025).

    Article  ADS  Google Scholar 

  74. Bravyi, S., DiVincenzo, D. P. & Loss, D. Schrieffer–Wolff transformation for quantum many-body systems. Ann. Phys. 326, 2793–2826 (2011).

    Article  ADS  MathSciNet  Google Scholar 

  75. Bluvstein, D. et al. Controlling quantum many-body dynamics in driven Rydberg atom arrays. Science 371, 1355–1359 (2021).

    Article  ADS  MathSciNet  Google Scholar 

  76. Lesanovsky, I. & Katsura, H. Interacting Fibonacci anyons in a Rydberg gas. Phys. Rev. A 86, 041601 (2012).

    Article  ADS  Google Scholar 

  77. Datla, P. R. et al. Dataset for ‘Statistical localization of U(1) lattice gauge theory in a Rydberg simulator’. Zenodo https://doi.org/10.5281/zenodo.18012627 (2026).

Download references

Acknowledgements

We acknowledge earlier contributions to the experiment construction from W. Tian, F. Jia, W. J. Wee, A. Qu and J. You, as well as helpful discussions with M. M. Aliyu. W.W.H. is supported by the National Research Foundation (NRF), Singapore, through the NRF Fellowship NRF-NRFF15-2023-0008, and through the National Quantum Office, hosted in A*STAR, under its Centre for Quantum Technologies Funding Initiative (grant no. S24Q2d0009). N.K. acknowledges funding in part from the NSF STAQ Program (PHY-1818914). H.L. acknowledges support from the Alfred P. Sloan Foundation.

Author information

Authors and Affiliations

  1. Centre for Quantum Technologies and Department of Physics, National University of Singapore, Singapore, Singapore

    Prithvi Raj Datla, Luheng Zhao, Wen Wei Ho & Huanqian Loh

  2. Department of Physics, Stanford University, Stanford, CA, USA

    Prithvi Raj Datla

  3. Duke Quantum Center, Duke University, Durham, NC, USA

    Luheng Zhao, Natalie Klco & Huanqian Loh

  4. Department of Electrical and Computer Engineering, Duke University, Durham, NC, USA

    Luheng Zhao & Huanqian Loh

  5. Department of Physics, Duke University, Durham, NC, USA

    Natalie Klco & Huanqian Loh

Authors
  1. Prithvi Raj Datla
    View author publications

    Search author on:PubMed Google Scholar

  2. Luheng Zhao
    View author publications

    Search author on:PubMed Google Scholar

  3. Wen Wei Ho
    View author publications

    Search author on:PubMed Google Scholar

  4. Natalie Klco
    View author publications

    Search author on:PubMed Google Scholar

  5. Huanqian Loh
    View author publications

    Search author on:PubMed Google Scholar

Contributions

P.R.D. and L.Z. ran the experiments and developed the theory simulations. W.W.H. and N.K. guided the theory work. H.L. supervised the project. All authors discussed the results and contributed to the manuscript.

Corresponding author

Correspondence to Huanqian Loh.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Aaron Young and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Mapping from a chain of Rydberg atoms to a U(1) LGT.

a, The atomic chain of ground and Rydberg atoms is first mapped to b, a chain of electric field strings on the bonds and charge clusters on the sites. Internal states of the atoms (ground or Rydberg) are mapped directly to electric field variables on the bonds, where right-facing strings alternate in correspondence between ground and Rydberg state atoms on odd and even bonds (vice versa for left-facing strings). c, Another mapping is performed to finally arrive at a spin representation. On odd sites, spin down (spin up) corresponds to a negative charge (vacua), whereas on even sites, spin down (spin up) corresponds to a vacua (positive charge). d, Tracing out the bond degrees of freedom leads to constrained spin dynamics on the matter sites, where spin-exchange is allowed between adjacent sites, only if the surrounding two sites are both spin-up or spin-down.

Extended Data Fig. 2 A comparison of dynamics with (red bars) and without (blue bars) position disorder.

We plot time-averaged Z-microstate projections \({\overline{P}}_{k}\) evolving from an initial state within \({{\mathcal{K}}}_{11}\) (Extended Data Table 1). The two distributions appear similar, indicating only a minor localizing effect from the position disorder.

Extended Data Fig. 3 SLIOM distributions sampled from \({{\mathcal{H}}}_{{N}_{c}=5}\), but without postselection into \({\mathcal{S}}\).

The distributions are more spread out towards the right side of the chain. This is because state preparation infidelity, our main source of imperfection, is more likely to result in initializing a state with \({N}_{c}^{{\prime} } < 5\) compared to \({N}_{c}^{{\prime} } > 5\) (since \({{\mathcal{F}}}_{g} > {{\mathcal{F}}}_{r}\)). States belonging to a symmetry sector with Nc < 5 would naturally have their conserved charges more spread out across the chain, resulting in the broadening of distributions. Error bars depict the standard error of the mean.

Extended Data Fig. 4 Dynamics under HPPXPQ+QPXPP.

Atoms may flip their spins only if both of their nearest neighbors are in the ground state and exactly one of their next-nearest neighbors is in the Rydberg state. Schematically, these spin-flip conditions apply to atoms that 1. are not enveloped within the blockade radius of one of its next-nearest neighbors and 2. simultaneously intersect the facilitation shell of the other next-nearest neighbor. These conditions are realized by setting the global detuning to be the van der Waals interaction between two Rydberg atoms that are next-nearest neighbors, \(\varDelta\) = V1.

Extended Data Fig. 5 Effects of longer-range couplings.

a, Autocorrelators and b, microstate distributions are compared between the ideal case of V2 = 0 and the experimentally relevant case of V2 = 0.1Ω through numerical simulations.

Extended Data Fig. 6 Strong fragmentation in HLGT.

a, The number of Krylov fragments, NKrylov, scales exponentially as 1.22N. b, The size of the largest fragment Dmax as a fraction of the total Hilbert space dimension Dtotal vanishes for large N, indicating strong fragmentation. c, The fraction of fragments that are frozen (dimension one) approaches a finite value close to 1/3.

Extended Data Fig. 7 Typicality of SLIOM distributions for the \({{\mathcal{K}}}_{6}\) Krylov fragment.

a, Experimentally measured SLIOM distibutions, generated by temporal ensembles starting from Ωti = 0.56 and ending at Ωtf = 3 (open triangles), 4 (crosses), 5.6 (open circles). The error bars here depict the standard error of the mean. b, Numerically simulated SLIOM distibutions, generated by temporal ensembles (Ωti = 0.56, Ωtf = 5.6) starting from two different initial states (open circles for \(\left|\psi \right\rangle =\left|rgggggrggrgggggr\right\rangle \in {{\mathcal{K}}}_{6}\) and crosses for \(\left|{\psi }^{{\prime} }\right\rangle =\left|rgggrgrggrgrgggr\right\rangle \in {{\mathcal{K}}}_{6}\)) and compared with the infinite-temperature distribution within \({{\mathcal{K}}}_{6}\) (open triangles).

Extended Data Fig. 8 Scaling properties of the center SLIOM in the largest symmetry sector.

a, Full-width-half-maxima σ of the center SLIOM distributions over the system size N, evaluated for system sizes ranging from N = 90 to N = 450. The number of clusters in the largest symmetry sector does not necessarily increase with every increment in the system size, explaining the sawtooth feature in the plot that becomes less prominent for larger N. The fractional width is observed to scale with an exponent α = 0.49, in agreement with our results in the main text. b, A scaling collapse of center SLIOM distributions shows that their width indeed appears to scale as \(\sqrt{N}\). The site index i is plotted such that the center site on the chain of particles corresponds to i = 0. Each curve has a jagged feature between half-integer sites and integer sites, leading to separated Bell-shaped distributions.

Extended Data Table 1 Krylov fragments within the Nc = 5 symmetry sector
Full size table

Extended data

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Datla, P.R., Zhao, L., Ho, W.W. et al. Statistical localization of U(1) lattice gauge theory in a Rydberg simulator. Nat. Phys. (2026). https://doi.org/10.1038/s41567-026-03183-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Version of record:

  • DOI: https://doi.org/10.1038/s41567-026-03183-w

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing