Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Optical clock comparison for Lorentz symmetry testing

Nature volume 567, pages 204–208 (2019)Cite this article

Subjects

Abstract

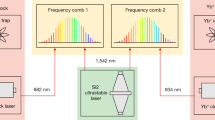
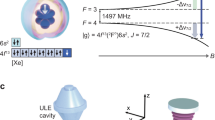
Questioning basic assumptions about the structure of space and time has greatly enhanced our understanding of nature. State-of-the-art atomic clocks1,2,3 make it possible to precisely test fundamental symmetry properties of spacetime and search for physics beyond the standard model at low energies of just a few electronvolts4. Modern tests of Einstein’s theory of relativity try to measure so-far-undetected violations of Lorentz symmetry5; accurately comparing the frequencies of optical clocks is a promising route to further improving such tests6. Here we experimentally demonstrate agreement between two single-ion optical clocks at the 10−18 level, directly validating their uncertainty budgets, over a six-month comparison period. The ytterbium ions of the two clocks are confined in separate ion traps with quantization axes aligned along non-parallel directions. Hypothetical Lorentz symmetry violations5,6,7 would lead to periodic modulations of the frequency offset as the Earth rotates and orbits the Sun. From the absence of such modulations at the 10−19 level we deduce stringent limits of the order of 10−21 on Lorentz symmetry violation parameters for electrons, improving previous limits8,9,10 by two orders of magnitude. Such levels of precision will be essential for low-energy tests of future quantum gravity theories describing dynamics at the Planck scale4, which are expected to predict the magnitude of residual symmetry violations.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Testing Lorentz symmetry with two earthbound optical Yb+ clocks.
Fig. 2: Six-month-long frequency comparison between two ytterbium single-ion clocks operating on the 642-THz electric octupole transition.

Similar content being viewed by others

Data availability

All data obtained in the study are available from the corresponding author on reasonable request.

References

  1. Nicholson, T. L. et al. Systematic evaluation of an atomic clock at 2 × 10−18 total uncertainty. Nat. Commun. 6, 6896 (2015).

    Article  CAS  Google Scholar 

  2. Huntemann, N., Sanner, C., Lipphardt, B., Tamm, C. & Peik, E. Single-ion atomic clock with 3 × 10−18 systematic uncertainty. Phys. Rev. Lett. 116, 063001 (2016).

    Article  ADS  CAS  Google Scholar 

  3. McGrew, W. F. et al. Atomic clock performance enabling geodesy below the centimetre level. Nature 564, 87–90 (2018).

    Article  ADS  CAS  Google Scholar 

  4. Safronova, M. S. et al. Search for new physics with atoms and molecules. Rev. Mod. Phys. 90, 025008 (2018).

    Article  ADS  MathSciNet  CAS  Google Scholar 

  5. Mattingly, D. Modern tests of Lorentz invariance. Living Rev. Relativ. 8, lrr-2005-5 (2005).

    Article  Google Scholar 

  6. Kostelecký, V. A. & Vargas, A. J. Lorentz and CPT tests with clock-comparison experiments. Phys. Rev. D 98, 036003 (2018).

    Article  ADS  Google Scholar 

  7. Colladay, D. & Kostelecký, V. A. Lorentz-violating extension of the standard model. Phys. Rev. D 58, 116002 (1998).

    Article  ADS  Google Scholar 

  8. Altschul, B. Synchrotron and inverse Compton constraints on Lorentz violations for electrons. Phys. Rev. D 74, 083003 (2006).

    Article  ADS  MathSciNet  Google Scholar 

  9. Hohensee, M. A. et al. Limits on violations of Lorentz symmetry and the Einstein equivalence principle using radio-frequency spectroscopy of atomic dysprosium. Phys. Rev. Lett. 111, 050401 (2013).

    Article  ADS  CAS  Google Scholar 

  10. Pruttivarasin, T. et al. Michelson–Morley analogue for electrons using trapped ions to test Lorentz symmetry. Nature 517, 592–595 (2015).

    Article  ADS  CAS  Google Scholar 

  11. Kennedy, R. J. & Thorndike, E. M. Experimental establishment of the relativity of time. Phys. Rev. 42, 400–418 (1932).

    Article  ADS  Google Scholar 

  12. Kostelecký, V. A. & Russell, N. Data tables for Lorentz and CPT violation. Rev. Mod. Phys. 83, 11–31 (2011).

    Article  ADS  Google Scholar 

  13. Hughes, V. W., Robinson, H. G. & Beltran-Lopez, V. Upper limit for the anisotropy of inertial mass from nuclear resonance experiments. Phys. Rev. Lett. 4, 342–344 (1960).

    Article  ADS  Google Scholar 

  14. Drever, R. W. P. A search for anisotropy of inertial mass using a free precession technique. Philos. Mag. 6, 683–687 (1961).

    Article  ADS  Google Scholar 

  15. Müller, H., Herrmann, S., Saenz, A., Peters, A. & Lämmerzahl, C. Optical cavity tests of Lorentz invariance for the electron. Phys. Rev. D 68, 116006 (2003).

    Article  ADS  Google Scholar 

  16. Müller, H. Testing Lorentz invariance by the use of vacuum and matter filled cavity resonators. Phys. Rev. D 71, 045004 (2005).

    Article  ADS  Google Scholar 

  17. Megidish, E., Broz, J., Greene, N. & Häffner, H. Entanglement enhanced precision test of local Lorentz invariance. Preprint at https://arxiv.org/abs/1809.09807 (2018).

  18. Campbell, S. L. et al. A Fermi-degenerate three-dimensional optical lattice clock. Science 358, 90–94 (2017).

    Article  ADS  CAS  Google Scholar 

  19. Dzuba, V. A. et al. Strongly enhanced effects of Lorentz symmetry violation in entangled Yb+ ions. Nat. Phys. 12, 465–468 (2016).

    Article  CAS  Google Scholar 

  20. Kostelecký, V. A. & Lane, C. D. Constraints on Lorentz violation from clock-comparison experiments. Phys. Rev. D 60, 116010 (1999).

    Article  ADS  Google Scholar 

  21. Kostelecký, V. A. & Mewes, M. Signals for Lorentz violation in electrodynamics. Phys. Rev. D 66, 056005 (2002).

    Article  ADS  Google Scholar 

  22. Kostelecký, V. A. & Tasson, J. D. Matter-gravity couplings and Lorentz violation. Phys. Rev. D 83, 016013 (2011).

    Article  ADS  Google Scholar 

  23. Ludlow, A. D., Boyd, M. M., Ye, J., Peik, E. & Schmidt, P. O. Optical atomic clocks. Rev. Mod. Phys. 87, 637–701 (2015).

    Article  ADS  CAS  Google Scholar 

  24. Tamm, C. et al. Cs-based optical frequency measurement using cross-linked optical and microwave oscillators. Phys. Rev. A 89, 023820 (2014).

    Article  ADS  Google Scholar 

  25. Roos, C. F., Chwalla, M., Kim, K., Riebe, M. & Blatt, R. ‘Designer atoms’ for quantum metrology. Nature 443, 316–319 (2006).

    Article  ADS  CAS  Google Scholar 

  26. Bluhm, R., Kostelecký, V. A., Lane, C. D. & Russell, N. Probing Lorentz and CPT violation with space-based experiments. Phys. Rev. D 68, 125008 (2003).

    Article  ADS  Google Scholar 

  27. Matei, D. G. et al. 1.5 μm lasers with sub-10 mHz linewidth. Phys. Rev. Lett. 118, 263202 (2017).

    Article  ADS  CAS  Google Scholar 

  28. Zanon-Willette, T. et al. Composite laser-pulses spectroscopy for high-accuracy optical clocks: a review of recent progress and perspectives. Rep. Prog. Phys. 81, 094401 (2018).

    Article  ADS  Google Scholar 

  29. Yudin, V. I. et al. Hyper-Ramsey spectroscopy of optical clock transitions. Phys. Rev. A 82, 011804 (2010).

    Article  ADS  Google Scholar 

  30. Taichenachev, A. V. et al. Compensation of field-induced frequency shifts in Ramsey spectroscopy of optical clock transitions. JETP Lett. 90, 713–717 (2010).

    Article  ADS  Google Scholar 

  31. Delva, P. et al. Test of special relativity using a fiber network of optical clocks. Phys. Rev. Lett. 118, 221102 (2017).

    Article  ADS  CAS  Google Scholar 

  32. Shaniv, R. et al. New methods for testing Lorentz invariance with atomic systems. Phys. Rev. Lett. 120, 103202 (2018).

    Article  ADS  CAS  Google Scholar 

  33. Doležal, M. et al. Analysis of thermal radiation in ion traps for optical frequency standards. Metrologia 52, 842–856 (2015).

    Article  ADS  Google Scholar 

  34. Keller, J., Partner, H. L., Burgermeister, T. & Mehlstäubler, T. E. Precise determination of micromotion for trapped-ion optical clocks. J. Appl. Phys. 118, 104501 (2015); correction 119, 059902 (2016).

    Article  ADS  Google Scholar 

  35. Dubé, P., Madej, A. A., Zhou, Z. & Bernard, J. E. Evaluation of systematic shifts of the 88Sr+ single-ion optical frequency standard at the 10−17 level. Phys. Rev. A 87, 023806 (2013).

    Article  ADS  Google Scholar 

  36. Godun, R. M. et al. Frequency ratio of two optical clock transitions in 171Yb+ and constraints on the time variation of fundamental constants. Phys. Rev. Lett. 113, 210801 (2014).

    Article  ADS  CAS  Google Scholar 

  37. Rosenband, T. et al. Frequency ratio of Al+ and Hg+ single-ion optical clocks; metrology at the 17th decimal place. Science 319, 1808–1812 (2008).

    Article  ADS  CAS  Google Scholar 

Download references

Acknowledgements

We thank B. Altschul, A. Goban, R. Hutson, A. Kostelecký, T. Mehlstäubler, M. Mewes, A. Vargas-Silva and J. Zhang for discussions and B. Lipphardt for experimental assistance. This research received funding from the European Metrology Programme for Innovation and Research (EMPIR project OC18), co-financed by the Participating States and the European Union’s Horizon 2020 research and innovation programme, and from DFG through CRC 1227 (DQ-mat). This work was also supported in part by the Office of Naval Research, USA, under award number N00014-17-1-2252, by NSF through grant PHY-1620687 (USA) and by the Russian Foundation for Basic Research under grant number 17-02-00216. C.S. thanks the Humboldt Foundation for support.

Author information

Author notes

  1. Christian Sanner

    Present address: JILA, Boulder, CO, USA

Authors and Affiliations

  1. Physikalisch-Technische Bundesanstalt, Braunschweig, Germany

    Christian Sanner, Nils Huntemann, Richard Lange, Christian Tamm & Ekkehard Peik

  2. Department of Physics and Astronomy, University of Delaware, Newark, DE, USA

    Marianna S. Safronova & Sergey G. Porsev

  3. Joint Quantum Institute, National Institute of Standards and Technology and the University of Maryland, College Park, MD, USA

    Marianna S. Safronova

  4. Petersburg Nuclear Physics Institute of NRC (Kurchatov Institute), Gatchina, Russia

    Sergey G. Porsev

Authors
  1. Christian Sanner
    View author publications

    Search author on:PubMed Google Scholar

  2. Nils Huntemann
    View author publications

    Search author on:PubMed Google Scholar

  3. Richard Lange
    View author publications

    Search author on:PubMed Google Scholar

  4. Christian Tamm
    View author publications

    Search author on:PubMed Google Scholar

  5. Ekkehard Peik
    View author publications

    Search author on:PubMed Google Scholar

  6. Marianna S. Safronova
    View author publications

    Search author on:PubMed Google Scholar

  7. Sergey G. Porsev
    View author publications

    Search author on:PubMed Google Scholar

Contributions

C.S., N.H. and E.P. conceived the experiment and developed the methods. C.S., N.H., R.L. and C.T. designed and constructed the experimental apparatus. C.S., N.H., R.L., M.S.S. and S.G.P. acquired and analysed the data. All authors were involved in the preparation and discussion of the manuscript.

Corresponding author

Correspondence to Christian Sanner.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

This file contains details about the transformation between lab frame and celestial frame and derives explicit formulas for the matrix elements of the T0(2) operator.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sanner, C., Huntemann, N., Lange, R. et al. Optical clock comparison for Lorentz symmetry testing. Nature 567, 204–208 (2019). https://doi.org/10.1038/s41586-019-0972-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41586-019-0972-2

This article is cited by

Comments

Commenting on this article is now closed.

  1. Xinhang Shen

    Dear Christian Sanner, Nils Huntemann, Richard Lange, Christian Tamm, Ekkehard Peik, Marianna S. Safronova & Sergey G. Porsev,

    It has been more than three years during which I have posted numerous comments here to show that Einstein's relativity is wrong and there is no such thing called spacetime in nature because time is absolute and independent of the three dimensional space. If you have found errors in my reasoning, please refute them. Otherwise, you should accept the discovery. I think it would be inappropriate to ignore this discovery and continue wasting taxpayers' money on wrong researches.

    Here is a summary of the reasoning to disprove special relativity for your convenience:

    Let's look at the twin paradox which is designed to demonstrate that relative speed would generate time dilation as predicted by special relativity which claims that when the speed of a clock relative to an observer was close to the speed of light, the observer would see the clock slow down close to stop. But, as shown on Wikipedia, the final conclusion of the twin paradox becomes that, after a high speed space travel, it is the acceleration of the traveling twin (not his speed relative to his brother) that made him younger than his twin brother staying on the earth because both twins had experienced exactly the same speed relative to each other during the entire trip. Is it funny that the original argument that relative speed generates time dilation is completely lost, although relativists still think that the paradox has been solved? In fact, this paradox has simply confirmed that relative speed can never generate time dilation and special relativity is wrong.

    Actually Einstein's relativity has already been disproved both theoretically and experimentally for more than three years. The fatal mistake of Einstein’s relativity is that it uses Lorentz Transformation to redefine time and space and the newly defined time is no longer the physical time we measure with physical clocks. We know the physical time shown on any physical clock is T = tf/k where t is the theoretical time, f is the frequency of the clock and k is a reference frame independent calibration constant.

    In Newton’s mechanics, f is a reference frame independent constant too. Therefore, we can set k = f to make the clock show the theoretical time i.e. the absolute Galilean time t: T = tf/k = tf/f = t.

    But in special relativity, frequency f is a reference frame dependent variable and can’t be eliminated by setting k = f. Thus, T can never be relativistic time t: T = tf/k != t. Therefore, relativistic time t is never the clock time i.e. the physical time which we are using to observe all physical phenomena. On the other hand, when a clock is observed in another inertial reference frame, we have t’ = rt and f’ = f/r and T’ = t’f’/k = rt(f/r)/k = tf/k = T, where r = 1/sqrt(1 - v^2/c^2), which means that the physical time T won’t change with the change of the inertial reference frame, and is Lorentz invariant and absolute. That is, a clock still measures the absolute time in special relativity.

    This absoluteness of the physical time can be more clearly illustrated by the following thought experiment:

    There are a series of vertically standing candles with the same burning rate and moving at different constant horizontal velocities in an inertial reference frame of (x, y, z, t) where x, y, z, t are relativistic space coordinates and time. At any moment t of relativistic time, all candles have the same height H in the reference frame of (x, y, z, t) and the height has been calibrated as the physical time. Therefore, we have the simultaneous events measured in both relativistic time t and physical time H in the frame of (x, y, z, t): (Candle1, x1, y1, H, t), (candle2, x2, y2, H, t), ... (CandleN, xn, yn, H, t). When these events are observed in anther horizontally moving inertial reference frame (x', y', z', t'), according to special relativity, these events can be obtained through Lorentz Transformation: (Candle1, x'1, y'1, H, t'1), (Candle2, x'2, y'2, H, t'2), ... (CandleN, x'n, y'n, H, t'n) where t'1, t'2, ... and t'n are relativistic times of the events observed in the frame of (x', y', z', t'). It is seen these events have different relativistic times after Lorentz Transformation in the frame of (x', y', z', t'), i.e., they are no longer simultaneous measured with relativistic time in the frame of (x', y', z', t'), but the heights of the candles remain the same because the vertical heights here do not experience any Lorentz contraction. Since the heights of the candles are the measures of the physical time, we can see these events still have the same physical time, i.e., they are still simultaneous measured with the physical time. Therefore, the physical time is invariant of inertial reference frames and absolute, which is completely different from relativistic time.

    As relativistic time is not the physical time we measure with physical clocks, all what special relativity describes is irrelevant to real physics.

    That the physical time (i.e. clock time) is absolute has been clearly confirmed by the physical fact that all the atomic clocks on the GPS satellites are synchronized not only relative to the ground clocks but also relative to each other to show the same absolute physical time, which directly denies the claim of special relativity that clocks can never be synchronized relative to more than one inertial reference frame no matter how you correct them because "time is relative".

    You will find the mathematical proofs that in special relativity, the real speed of light still follows Newton's velocity addition law, and both time dilation and length contraction are simply illusions in my peer-reviewed publications which are available free of charge at: https://www.researchgate.ne... and https://www.researchgate.ne...

    If you don't agree, your refutation will be welcome and greatly appreciated.

    Sincerely,

    Xinhang Shen

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing