Abstract
General relativity1 predicts that short-orbital-period binaries emit considerable amounts of gravitational radiation. The upcoming Laser Interferometer Space Antenna2 (LISA) is expected to detect tens of thousands of such systems3 but few have been identified4, of which only one5 is eclipsing—the double-white-dwarf binary SDSS J065133.338+284423.37, which has an orbital period of 12.75 minutes. Here we report the discovery of an eclipsing double-white-dwarf binary system, ZTF J153932.16+502738.8, with an orbital period of 6.91 minutes. This system has an orbit so compact that the entire binary could fit within the diameter of the planet Saturn. The system exhibits a deep eclipse, and a double-lined spectroscopic nature. We see rapid orbital decay, consistent with that expected from general relativity. ZTF J153932.16+502738.8 is a strong source of gravitational radiation close to the peak of LISA’s sensitivity, and we expect it to be detected within the first week of LISA observations, once LISA launches in approximately 2034.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Upon request, K.B.B. will provide reduced photometric and spectroscopic data, and available ZTF data for the object. We have included the eclipse time data used to construct the orbital decay diagram in Fig. 2a, and Extended Data Figs. 2 and 3. The X-ray observations are already in the public domain, and their observation IDs have been supplied in the text. The proprietary period for the spectroscopic data will expire at the start of 2020, at which point this data will also be public and readily accessible.
Code availability
Upon request, K.B.B. will provide the code (primarily in Python) used to analyse the observations and data such as the posterior distributions used to produce the figures in the text (MATLAB was used to generate most of the figures).
References
Einstein, A. Näherungsweise Integration der Feldgleichungen der Gravitation. Sitz. König. Preußisch. Akad. Wissenschaften 688–696 (1916).
Amaro-Seoane, P. et al. Laser interferometer space antenna. Preprint at https://arxiv.org/abs/1702.00786 (2017).
Nissanke, S., Vallisneri, M., Nelemans, G. & Prince, T. A. Gravitational-wave emission from compact galactic binaries. Astrophys. J. 758, 131 (2012).
Kupfer, T. et al. LISA verification binaries with updated distances from Gaia data release 2. Mon. Not. R. Astron. Soc. 480, 302–309 (2018).
Brown, W. R. et al. A 12-minute orbital period detached white dwarf eclipsing binary. Astrophys. J. Lett. 737, 23 (2011).
Bellm, E. C. et al. The Zwicky Transient Facility: system overview, performance, and first results. Publ. Astron. Soc. Pacif. 131, 018002 (2019).
Graham, M. J. et al. The Zwicky Transient Facility: science objectives. Publ. Astron. Soc. Pacif. 131, 078001 (2019).
Coughlin, M. W. et al. The Kitt Peak Electron Multiplying CCD demonstrator. Mon. Not. R. Astron. Soc. 485, 1412–1419 (2019).
Harding, L. K. et al. CHIMERA: a wide-field, multi-colour, high-speed photometer at the prime focus of the Hale telescope. Mon. Not. R. Astron. Soc. 457, 3036–3049 (2016).
Taylor, J. H., Fowler, L. & McCulloch, P. Measurements of general relativistic effects in the binary pulsar PSR1913 + 16. Nature 277, 437 (1979).
Masci, F. J. et al. The IPAC image subtraction and discovery pipeline for the Intermediate Palomar Transient Factory. Publ. Astron. Soc. Pacif. 129, 014002 (2017).
Law, N. M. et al. The Palomar Transient Factory: system overview, performance, and first results. Publ. Astron. Soc. Pacif. 121, 1395 (2009).
McCarthy, J. K. et al. Blue channel of the Keck low-resolution imaging spectrometer. In Optical Astronomical Instrumentation Vol. 3355, 81–93 (International Society for Optics and Photonics, 1998).
Hermes, J. et al. Rapid orbital decay in the 12.75-minute binary white dwarf J0651 + 2844. Astrophys. J. Lett. 757, 21 (2012).
Fuller, J. & Lai, D. Dynamical tides in compact white dwarf binaries: helium core white dwarfs, tidal heating and observational signatures. Mon. Not. R. Astron. Soc. 430, 274–287 (2013).
Shah, S., Nelemans, G. & van der Sluys, M. Using electromagnetic observations to aid gravitational-wave parameter estimation of compact binaries observed with LISA-II. The effect of knowing the sky position. Astron. Astrophys. 553, A82 (2013).
Holberg, J. & Bergeron, P. Calibration of synthetic photometry using DA white dwarfs. Astron. J. 132, 1221 (2006).
Istrate, A. G. et al. Models of low-mass helium white dwarfs including gravitational settling, thermal and chemical diffusion, and rotational mixing. Astron. Astrophys. 595, A35 (2016).
Ramsay, G., Cropper, M., Wu, K., Mason, K. & Hakala, P. Detection of the optical counterpart of the proposed double degenerate polar RX J1914 + 24. Mon. Not. R. Astron. Soc. 311, 75–84 (2000).
Roelofs, G. H. et al. Spectroscopic evidence for a 5.4 minute orbital period in HM Cancri. Astrophys. J. Lett. 711, 138 (2010).
Marsh, T. & Steeghs, D. V407 Vul: a direct impact accretor. Mon. Not. R. Astron. Soc. 331, L7–L11 (2002).
Gehrels, N. et al. The Swift gamma-ray burst mission. Astrophys. J. 611, 1005 (2004).
Jansen, F. et al. XMM-Newton observatory—I. The spacecraft and operations. Astron. Astrophys. 365, L1–L6 (2001).
Wolf, W. M., Bildsten, L., Brooks, J. & Paxton, B. Hydrogen burning on accreting white dwarfs: stability, recurrent novae, and the post-nova supersoft phase. Astrophys. J. 777, 136 (2013).
Kaplan, D. L., Bildsten, L. & Steinfadt, J. D. Orbital evolution of compact white dwarf binaries. Astrophys. J. 758, 64 (2012).
Marsh, T. R., Nelemans, G. & Steeghs, D. Mass transfer between double white dwarfs. Mon. Not. R. Astron. Soc. 350, 113–128 (2004).
Paczynski, B. Evolution of single stars. IV. Helium stars. Acta Astron. 21, 1 (1971).
Shen, K. J., Kasen, D., Miles, B. J. & Townsley, D. M. Sub-Chandrasekhar-mass white dwarf detonations revisited. Astrophys. J. 854, 52 (2018).
Bildsten, L., Townsley, D. M., Deloye, C. J. & Nelemans, G. The thermal state of the accreting white dwarf in AM Canum Venaticorum binaries. Astrophys. J. 640, 466 (2006).
Althaus, L. G., Camisassa, M. E., Bertolami, M. M. M., Córsico, A. H. & García-Berro, E. White dwarf evolutionary sequences for low-metallicity progenitors: the impact of third dredge-up. Astron. Astrophys. 576, A9 (2015).
Graham, M. J., Drake, A. J., Djorgovski, S., Mahabal, A. A. & Donalek, C. Using conditional entropy to identify periodicity. Mon. Not. R. Astron. Soc. 434, 2629–2635 (2013).
Bellm, E. C. et al. The Zwicky Transient Facility: surveys and scheduler. Publ. Astron. Soc. Pacif. 131, 068003 (2019).
Maxted, P. ellc: A fast, flexible lightcurve model for detached eclipsing binary stars and transiting exoplanets. Astron. Astrophys. 591, A111 (2016).
Gianninas, A., Strickland, B., Kilic, M. & Bergeron, P. Limb-darkening coefficients for eclipsing white dwarfs. Astrophys. J. 766, 3 (2013).
Claret, A. & Bloemen, S. Gravity and limb-darkening coefficients for the Kepler, CoRoT, Spitzer, uvby, UBVRIJHK, and Sloan photometric systems. Astron. Astrophys. 529, A75 (2011).
Shklovskii, I. Possible causes of the secular increase in pulsar periods. Sov. Astron. 13, 562 (1970).
Lorimer, D. R. & Kramer, M. Handbook of Pulsar Astronomy (Cambridge Univ. Press, 2012).
Brown, A. et al. Gaia data release 2—summary of the contents and survey properties. Astron. Astrophys. 616, A1 (2018).
Bovy, J. galpy: a Python library for galactic dynamics. Astrophys. J. Suppl. Ser. 216, 29 (2015).
Levenhagen, R. S., Diaz, M. P., Coelho, P. R. T. & Hubeny, I. A grid of synthetic spectra for hot DA white dwarfs and its application in stellar population synthesis. Astrophys. J. Suppl. Ser. 231, 1 (2017).
Horne, K. & Schneider, D. P. Evidence for a high-mass white dwarf in nova V1500 Cygni 1975. Astrophys. J. 343, 888–901 (1989).
Green, G. M. et al. Galactic reddening in 3d from stellar photometry—an improved map. Mon. Not. R. Astron. Soc. 478, 651–666 (2018).
Korol, V. et al. Prospects for detection of detached double white dwarf binaries with Gaia, LSST and LISA. Mon. Not. R. Astron. Soc. 470, 1894–1910 (2017).
Fuller, J. & Lai, D. Dynamical tides in compact white dwarf binaries: tidal synchronization and dissipation. Mon. Not. R. Astron. Soc. 421, 426–445 (2012).
Benacquista, M. J. Tidal perturbations to the gravitational inspiral of J0651 + 2844. Astrophys. J. Lett. 740, 54 (2011).
Paxton, B. et al. Modules for experiments in stellar astrophysics (MESA): binaries, pulsations, and explosions. Astrophys. J. Suppl. Ser. 220, 15 (2015).
Kalberla, P. M. et al. The Leiden/Argentine/Bonn (LAB) survey of galactic HI—final data release of the combined LDS and IAR surveys with improved stray-radiation corrections. Astron. Astrophys. 440, 775–782 (2005).
Fuller, J. & Lai, D. Tidal novae in compact binary white dwarfs. Astrophys. J. Lett. 756, L17 (2012).
Brown, W. R., Kilic, M., Kenyon, S. J. & Gianninas, A. Most double degenerate low-mass white dwarf binaries merge. Astrophys. J. 824, 46 (2016).
Bovy, J. & Rix, H.-W. A direct dynamical measurement of the Milky Way’s disk surface density profile, disk scale length, and dark matter profile at 4 kpc < R < 9 kpc. Astrophys. J. 779, 115 (2013).
Acknowledgements
K.B.B. thanks the National Aeronautics and Space Administration and the Heising Simons Foundation for supporting his research. This work was based on observations obtained with the Samuel Oschin Telescope 48-inch and the 60-inch Telescope at the Palomar Observatory as part of the Zwicky Transient Facility project. ZTF is supported by the National Science Foundation under grant number AST-1440341 and a collaboration including Caltech, IPAC, the Weizmann Institute for Science, the Oskar Klein Center at Stockholm University, the University of Maryland, the University of Washington (UW), Deutsches Elektronen-Synchrotron and Humboldt University, Los Alamos National Laboratories, the TANGO Consortium of Taiwan, the University of Wisconsin at Milwaukee, and the Lawrence Berkeley National Laboratories. Operations are conducted by Caltech Optical Observatories, IPAC, and the University of Washington. The KPED team thanks the National Science Foundation and the National Optical Astronomical Observatory for making the Kitt Peak 2.1-m telescope available. The KPED team thanks the National Science Foundation, the National Optical Astronomical Observatory and the Murty family for support in the building and operation of KPED. In addition, they thank the CHIMERA project for use of the Electron Multiplying CCD (EMCCD). Some of the data presented herein were obtained at the W. M. Keck Observatory, which is operated as a scientific partnership among the California Institute of Technology, the University of California and the National Aeronautics and Space Administration. The Observatory was made possible by the generous financial support of the W. M. Keck Foundation. We wish to recognize and acknowledge the very important cultural role and reverence that the summit of Mauna Kea has always had within the indigenous Hawaiian community. We are most fortunate to have the opportunity to conduct observations from this mountain. This research benefited from interactions at the ZTF Theory Network Meeting that were funded by the Gordon and Betty Moore Foundation through grant GBMF5076 and support from the National Science Foundation through PHY-1748958. We thank J. Hoffman, the creator of cuvarbase. We thank T. Marsh, S. Phinney and V. Korol for discussions. We thank G. Hallinan and C. Fremling for helping to observe the object.
Author information
Authors and Affiliations
Contributions
K.B.B. discovered the object, conducted the lightcurve analysis and eclipse time analysis, and was the primary author of the manuscript. K.B.B. and M.W.C. conducted the spectroscopic analysis. K.B.B., M.W.C. and T.A.P. conducted the combined mass–radius analysis. K.B.B. and M.W.C. reduced the optical data. K.B.B., M.W.C. and D.L.K. reduced and analysed the X-ray observations. J.F. conducted the theoretical analysis, including that on tides, and developed the MESA evolutionary models. K.B.B., M.W.C., T.K., S.R.K., J.v.R. and T.A.P. all contributed to collecting data on the object. K.B.B., M.W.C., J.F., T.K., E.C.B., L.B., M.J.G., D.L.K., J.v.R., S.R.K. and T.A.P. contributed to the physical interpretation of the object. T.K., E.C.B., R.G.D., M.F., M.G., S.K., R.R.L., A.A.M., F.J.M., R.R., D.L.S., M.T.S., R.M.S., P.S. and R.W. contributed to the implementation of ZTF; M.J.G. is the project scientist, T.A.P. and G.H. are co-PIs, and S.R.K. is the PI of ZTF. R.G.D., D.A.D., M.F. and R.R. contributed to the implementation of KPED; M.W.C. is project scientist, and S.R.K. is PI of KPED. T.A.P. is K.B.B.’s PhD advisor.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Peer review information Nature thanks Warren Brown and J. J. Hermes for their contribution to the peer review of this work.
Extended data figures and tables
Extended Data Fig. 1 Corner plots of lightcurve modelling.
The corner plots of the lightcurve fit to 12,999 g′ epochs taken with CHIMERA on 5, 6 and 7 July 2018. We note that the two limb-darkening coefficients, as well as the gravity darkening of the secondary (bottom three panels), were allowed to vary to ensure that assumptions regarding these coefficients were not strongly covariant with the other physical quantities of interest.
Extended Data Fig. 2 Fits to archival PTF/iPTF data.
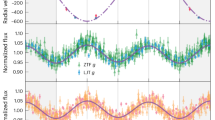
PTF least-squares fits of single harmonic sinusoids (smooth blue lines) to archival PTF/iPTF data used to determine the orbital decay rate. This archival data was extracted by using forced photometry on difference images. Because this is a least-squares fit of a sinusoid to the data, this timing technique uses the reflection effect in the system as its primary clock, rather than the mid-eclipse time. All error bars are 1σ. To determine the time of the epoch, we take the mean of all epochs used, and then calculate the phase of eclipse nearest to this mean time.
Extended Data Fig. 3 Orbital decay measured with CHIMERA and KPED.
A quadratic fit (smooth red curve) to timing epochs exclusively originating from CHIMERA and KPED data (with the 68% confidence interval shown by the red dashed lines). This solution yielded a \(\dot{P}\) consistent with the much more precise solution derived by including PTF/iPTF data. All error bars on the timing epochs are 1σ. The time on the x axis is measured with respect to the T0 reported in Table 1.
Extended Data Fig. 4 Radial-velocity measurements of ZTFJ1539 + 5027.
A plot of the measured Doppler shifts versus orbital phase for the primary and secondary. The primary eclipse occurs at orbital phase 0. In the top panel, we plot measured Doppler shifts of the more massive primary, extracted from 12 phase bins of coadded spectra. The dashed blue line illustrates the fit of a sinusoid to this data (adjusted R2 = 0.7118). The bottom panel shows the Doppler shift measurements of the secondary, and also the best-fit sinusoid to this data (adjusted R2 = 0.9757). Because of the low SNR of the spectra, these fits have large uncertainties (especially in the case of the primary, with its shallow and broad absorption lines). This is reflected in the broad distribution of possible masses associated with the spectroscopic constraint illustrated in Fig. 4. All error bars are 68% confidence intervals.
Extended Data Fig. 5 Binary evolution models.
Binary stellar evolution models for systems similar to ZTF J1539 + 5027. The top panel shows the mass transfer rate as a function of orbital period. Systems begin at large orbital period and move towards smaller periods owing to gravitational radiation, and in some cases they move back out owing to stable mass transfer. Except for high-mass donors with thin hydrogen envelopes \(\left({M}_{{\rm{do}}}=0.25\;{M}_{\odot },\;{M}_{{\rm{H}}}=6\times 1{0}^{-4}\;{M}_{\odot }\right.\), mass transfer is expected to begin at orbital periods longer than 7 min. The bottom panel shows the corresponding accretion temperature from equation (11).
Extended Data Fig. 6 X-ray and optical constraints on accretion in ZTFJ1539 + 5027.
These constraints on mass transfer result from the non-detection of any signatures of accretion in both the optical and X-ray bands. The upper limits are expressed in terms of the mass accretion rate contributing to the accretion luminosity of a hypothetical hotspot. The solid red curve illustrates the constraint imposed by the XMM EPIC-pn X-ray non-detection, which rules out statistically significant mass transfer contributing to a hotspot with temperatures greater than about 150,000 K, while the green dotted line illustrates a weaker upper limit imposed by the non-detection in a SWIFT XRT observation. We constructed the dashed blue curve, which represents the optical constraint, by requiring that any accretion luminosity originating from a hotspot should contribute <10% to the luminosity in the band ranging from 320 nm to 540 nm, as we know from the optical spectrum (Fig. 3) that this light is dominated by the approximately 50,000-K photosphere of the hot primary, and also we see no signature of a hotspot in the CHIMERA lightcurve (Fig. 1). We chose the threshold of <10% because, given the SNR of the spectra, we expect we should be able to detect optically thin emission with an amplitude at the 10% level. Other white dwarfs with such a hotspot (such as HM Cancri) exhibit such emission, particularly in lines associated with ionized helium.
Source data
Rights and permissions
About this article
Cite this article
Burdge, K.B., Coughlin, M.W., Fuller, J. et al. General relativistic orbital decay in a seven-minute-orbital-period eclipsing binary system. Nature 571, 528–531 (2019). https://doi.org/10.1038/s41586-019-1403-0
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41586-019-1403-0
This article is cited by
-
A seven-Earth-radius helium-burning star inside a 20.5-min detached binary
Nature Astronomy (2024)
-
A rotating white dwarf shows different compositions on its opposite faces
Nature (2023)
-
Astrophysics with the Laser Interferometer Space Antenna
Living Reviews in Relativity (2023)
-
A 62-minute orbital period black widow binary in a wide hierarchical triple
Nature (2022)
-
A dense 0.1-solar-mass star in a 51-minute-orbital-period eclipsing binary
Nature (2022)



VIadoIphPutIer
7,500 miles away, but why that fact couldn't be mentioned in the abstract is beyond me.
Xinhang Shen
Nature Editors and Kevin B. Burdge, Michael W. Coughlin, Thomas A. Prince,
Einstein's relativity has already been disproved theoretically and experimentally (see peer-reviewed published papers: https://www.researchgate.ne... and https://www.researchgate.ne... ). The fatal mistake of Einstein’s relativity is that it uses Lorentz Transformation to redefine time and space and the newly defined time is no longer the physical time we measure with physical clocks as illustrated in the following:
In classical mechanics, in an inertial reference frame (X, Y, Z, T), time T is the absolute Galilean time and space (X, Y, Z) is the rigid Galilean space, which follows Galilean Transformation when observed from another inertial reference frame (X', Y', Z', T'):
T' = T
X' = X - vT
Y' = Y
Z' = Z
where v is the speed of the reference reframe (X', Y', Z', T') relative to the reference frame (X, Y, Z, T). In order to produce a constant speed of light relative to all inertial reference frames, Einstein introduces Lorentz Transformation which is mathematically equivalent to a new definition of time (relativistic time t) and space (relativistic space x, y, z):
In an inertial reference frame with isotropic speed of light, he defines time and space as follows:
t = T
x = X
y = Y
z = Z
and in any other inertial reference frame (X', Y', Z', T') with a velocity v relative to the previous inertial reference frame, he defines time t' and space (x', y', z') as:
t' = (1/γ)T' - (γv/c^2)X'
x' = γX'
y' = Y'
z' = Z'
where
γ = 1/(1 - v^2/c^2)^(1/2)
With this definition of time and space, we can derive the relationship between (x, y, z, t) and (x', y', z', t') as follows:
t' = (1/γ)T' - (γv/c^2)X'
= (1/γ)T - (γv/c^2)(X - vT)
= (1/γ)t - (γv/c^2)(x - vt)
= (1/γ + γv^2/c^2)t - (γv/c^2)x
= γ(1/γ^2+ v^2/c^2)t - (γv/c^2)x
= γ(1-v^2/c^2+ v^2/c^2)t - (γv/c^2)x
= γt - (γv/c^2)x
= γ(t - vx/c^2)
x' = γX'
= γ(X - vT)
= γ(x - vt)
y' = Y'
= Y
= y
z' = Z'
= Z
= z
i.e.
t' = γ(t - vx/c^2)
x' = γ(x - vt)
y' = y
z' = z
This is Lorentz Transformation between two inertial reference frames. That is, all what special relativity does is just a redefinition of time and space. As the new definition of time and space is just a new coordinate system and should not influence the behavior of any physical process including any clock, like the geometry of a circle which is the same no matter whether you use a Cartesian coordinate system or a cylindrical coordinate system to study it, all the problems of relativity are arisen from the mistake equating relativistic time to the time of a real physical clock. We know the physical time Tp shown on any physical clock is
Tp= Ttf/k
where Tt is the theoretical time, f is the frequency of the clock and k is a reference frame independent calibration constant. In Newton’s mechanics, the theoretical time Tt is the absolute Galilean time T, and f is a reference frame independent constant too. Therefore, we can set
k = f
to make the clock show the theoretical time i.e. the absolute Galilean time T:
Tp= Ttf/k = Tf/f = T.
But in special relativity, the theoretical time Tt is the reference frame dependent relativistic time t which makes frequency f a reference frame dependent variable too. When a clock is observed in another inertial reference frame, we have
Tt' = t’ = γt
f’ = f/γ
Tp’ = Tt'f'/k = t’f’/k = (γt)(f/γ)/k = tf/k = Tp
This means that the physical time Tp won’t change with the change of the inertial reference frame, and is Lorentz invariant and absolute, i.e., a clock still measures the absolute Galilean time in special relativity because the effect of the dilation of relativistic time is always canceled by the decrease of its frequency in a physical clock. The absoluteness of the physical time can be more clearly illustrated by the following thought experiment:
There are a series of vertically standing candles with the same ideal burning rate and moving at different constant horizontal velocities relative to an inertial reference frame of (x, y, z, t) where x, y, z, t are relativistic space coordinates and time. At any moment t of relativistic time, all candles have the same height H in the reference frame of (x, y, z, t) and the height has been calibrated as the physical time. Therefore, we have the simultaneous events measured in both relativistic time t and physical time H in the frame of (x, y, z, t): (Candle1, x1, y1, H, t), (candle2, x2, y2, H, t), ... (CandleN, xn, yn, H, t). When these events are observed in anther horizontally moving inertial reference frame (x', y', z', t'), according to special relativity, these events can be obtained through Lorentz Transformation: (Candle1, x'1, y'1, H, t'1), (Candle2, x'2, y'2, H, t'2), ... (CandleN, x'n, y'n, H, t'n) where t'1, t'2, ... and t'n are relativistic times of the events observed in the frame of (x', y', z', t'). It is seen these events have different relativistic times t'1, t'2, ... and t'n after Lorentz Transformation in the frame of (x', y', z', t'), i.e., they are no longer simultaneous measured with relativistic time in the frame of (x', y', z', t'), but the heights of the candles remain the same because the vertical heights here do not experience any Lorentz contraction. Since the heights of the candles are the measures of the physical time, we can see these events still have the same physical time, i.e., they are still simultaneous measured with the physical time. Therefore, the physical time is invariant of inertial reference frames and absolute, which is completely different from relativistic time.
With the above relationship between Galilean space and time and relativistic space and time, we can also get Galilean space and time as functions of relativistic space and time, that is, we can say that Galilean space and time still exists in special relativity. In the inertial reference frame with isotropic speed of light, we have:
T = t
X= x
Y = y
Z = z
In any other inertial reference frame (x', y', z', t'), we have:
T' = γ(t' + vx'/c^2)
X' = x'/γ
Y' = y'
Z' = z'
As the real speed of light is measured with a physical clock which is absolute Galilean time, the real speed of light should be defined by Galilean time and space. Now we can use special relativity to prove that the real speed of light is not constant but still follows Newton's velocity addition formula.
In the moving frame, we have the real speed of light:
C' = X'/T' = (x'/γ)/[γ(t + vx/c^2)] = [(x'/t')/γ^2]/[1 + (v/c^2)(x'/t')]
Since x'/t' is the relativistic speed of light which is always a constant c, we have:
C' = [(x'/t')/γ^2]/[1 + (v/c^2)(x'/t')] = [(c)(1 - v^2/c^2)]/[1 + (v/c^2)(c)] = c - v
Since in the inertial reference frame with isotropic speed of light, Galilean time and space is the same as relativistic time and space, we have c = t/x = T/X = C and thus:
C' = C - v
Therefore, the real speed of light is not constant but still follows Newton's velocity addition formula, which directly denies the postulate of special relativity that the speed of light is constant relative to all inertial reference frames. You can also find detail mathematical proofs that both time dilation and length contraction are illusions in my peer-reviewed published papers as shown above.
The absoluteness of the physical time has been clearly confirmed by the physical experimental evidence that, after all corrections, all the atomic clocks on the GPS satellites are synchronized not only relative to the ground clocks but also relative to each other (i.e. they are synchronized relative to all reference frames) to show the same absolute physical time, which directly denies the claim of special relativity that clocks can never be synchronized relative to more than one inertial reference frame no matter how you correct them because "time is relative" and "simultaneity can be held only in one inertial reference frame".
As relativistic time is not the physical time we measure with physical clocks, all what relativity describes is irrelevant to real physical phenomena.
I wonder why you continue publishing articles on the wrong theory and look forward to seeing your explanation.
Sincerely,
Xinhang Shen