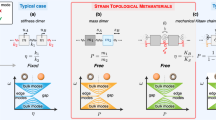
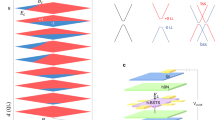
Abstract
Introducing the concept of topology has revolutionized materials classification, leading to the discovery of topological insulators and Dirac–Weyl semimetals1,2,3. One of the most fundamental theories underpinning topological materials is the Su–Schrieffer–Heeger (SSH) model4,5, which was developed in 1979—decades before the recognition of topological insulators—to describe conducting polymers. Distinct from the vast majority of known topological insulators with two and three dimensions1,2,3, the SSH model predicts a one-dimensional analogue of topological insulators, which hosts topological bound states at the endpoints of a chain4,5,6,7,8. To establish this unique and pivotal state, it is crucial to identify the low-energy excitations stemming from bound states, but this has remained unknown in solids because of the absence of suitable platforms. Here we report unusual electronic states that support the emergent bound states in elemental tellurium, the single helix of which was recently proposed to realize an extended version of the SSH chain9,10. Using spin- and angle-resolved photoemission spectroscopy with a micro-focused beam, we have shown spin-polarized in-gap states confined to the edges of the (0001) surface. Our density functional theory calculations indicate that these states are attributed to the interacting bound states originating from the one-dimensional array of SSH tellurium chains. Helices in solids offer a promising experimental platform for investigating exotic properties associated with the SSH chain and exploring topological phases through dimensionality control.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available within the main text and the extended data. Any other relevant data are available from the corresponding author upon request.
References
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Ando, Y. Topological insulator materials. J. Phys. Soc. Jpn 82, 102001 (2013).
Su, W. P., Schrieffer, J. R. & Heeger, A. J. Solitons in polyacetylene. Phys. Rev. Lett. 42, 1698–1701 (1979).
Su, W. P., Schrieffer, J. R. & Heeger, A. J. Soliton excitations in polyacetylene. Phys. Rev. B 22, 2099–2111 (1980).
Heeger, A. J., Kivelson, S., Schrieffer, J. R. & Su, W.-P. Solitons in conducting polymers. Rev. Mod. Phys. 60, 781–850 (1988).
Asbóth, J. K., Oroszlány, L. & Pályi, A. A Short Course on Topological Insulators: Band Structure and Edge States in One and Two Dimensions. Lecture Notes in Physics, Vol. 919 (Springer, 2016).
Guo, H. A brief review on one-dimensional topological insulators and superconductors. Sci. Chn. Phys. Mech. Astron. 59, 637401 (2016).
Kłosiński, A. et al. Topology of chalcogen chains. Phys. Rev. B 107, 125123 (2023).
Zhang, R. et al. Large shift current, π Zak phase, and the unconventional nature of Se and Te. Phys. Rev. Research 5, 023142 (2023).
Hsieh, D. et al. A tunable topological insulator in the spin helical Dirac transport regime. Nature 460, 1101–1105 (2009).
Konig, M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007).
Shi, B. et al. Phase transition and topological transistors based on monolayer Na3Bi nanoribbons. Nanoscale 13, 15048 (2021).
Wakatsuki, R., Ezawa, M., Tanaka, Y. & Nagaosa, N. Fermion fractionalization to Majorana fermions in a dimerized Kitaev superconductor. Phys. Rev. B 90, 014505 (2014).
Malkova, N., Hromada, I., Wang, X., Bryant, G. & Chen, Z. Observation of optical Shockley-like surface states in photonic superlattices. Opt. Lett. 34, 1633–1635 (2009).
Atala, M. et al. Direct measurement of the Zak phase in topological Bloch bands. Nat. Phys. 9, 795–800 (2013).
Cheon, S., Kim, T.-H., Lee, S.-H. & Yeom, H. W. Chiral solitons in a coupled double Peierls chain. Science 350, 182–185 (2015).
Drost, R., Teemu, O., Ari, H. & Peter, L. Topological states in engineered atomic lattices. Nat. Phys. 13, 668–671 (2017).
Li, P., Sau, J. D. & Appelbaum, I. Robust zero-energy bound states in a helical lattice. Phys. Rev. B 96, 115446 (2017).
Asnin, V. M. et al. “Circular” photogalvanic effect in optically active crystals. Solid State Commun. 30, 565–570 (1979).
Vorob’ev, E. L. et al. Optical activity in tellurium induced by a current. JETP Lett. 29, 441–445 (1979).
Shalygin, V. A., Sofronov, A. N., Vorob’ev, L. E. & Farbshtein, I. I. Current-induced spin polarization of holes in tellurium. Phys. Solid State 54, 2362–2373 (2012).
Yoda, T., Yokoyama, T. & Murakami, S. Current-induced Orbital and Spin Magnetizations in Crystals with Helical Structure. Sci Rep. 5, 12024 (2015).
Furukawa, T., Shimokawa, Y., Kobayashi, K. & Itou, T. Observation of current-induced bulk magnetization in elemental tellurium. Nat. Commun. 8, 954 (2017).
Tsirkin, S. S., Puente, P. A. & Souza, I. Gyrotropic effects in trigonal tellurium studied from first principles. Phys. Rev. B 97, 035158 (2018).
Hirayama, M., Okugawa, R., Ishibashi, S., Murakami, S. & Miyake, T. Weyl node and spin texture in trigonal tellurium and selenium. Phys. Rev. Lett. 114, 206401 (2015).
Nakayama, K. et al. Band splitting and Weyl nodes in trigonal tellurium studied by angle-resolved photoemission spectroscopy and density functional theory. Phys. Rev. B 95, 125204 (2017).
Sakano, M. et al. Radial spin texture in elemental tellurium with chiral crystal structure. Phys. Rev. Lett. 124, 136404 (2020).
Gatti, G. et al. Radial spin texture of the Weyl fermions in chiral tellurium. Phys. Rev. Lett. 125, 216402 (2020).
Qiu, G. et al. Quantum transport and band structure evolution under high magnetic field in few-layer tellurene. Nano Lett. 18, 5760–5767 (2018).
Qiu, G. et al. Quantum Hall effect of Weyl fermions in n-type semiconducting tellurene. Nat. Nanotechnol. 15, 585–591 (2020).
Zhang, N. et al. Magnetotransport signatures of Weyl physics and discrete scale invariance in the elemental semiconductor tellurium. Proc. Natl Acad. Sci. USA 117, 11337–11343 (2020).
Ideue, T. et al. Pressure-induced topological phase transition in noncentrosymmetric elemental tellurium. Proc. Natl Acad. Sci. USA 116, 25530–25534 (2019).
Chen, J. et al. Topological phase change transistors based on tellurium Weyl semiconductor. Sci. Adv. 8, eabn3837 (2022).
Lau, A., van den Brink, J. & Ortix, C. Topological mirror insulators in one dimension. Phys. Rev. B 94, 165164 (2016).
Li, P. & Appelbaum, I. Intrinsic two-dimensional states on the pristine surface of tellurium. Phys. Rev. B 97, 201402 (2018).
Zak, J. Berry’s phase for energy bands in solids. Phys. Rev. Lett. 62, 2747–2750 (1989).
Takayama, A., Sato, T., Souma, S., Oguchi, T. & Takahashi, T. One-dimensional edge states with giant spin splitting in a bismuth thin film. Phys. Rev. Lett. 114, 066402 (2015).
Andersson, S., Andersson, D. & Marklund, I. Clean Te surfaces studied by LEED. Surf. Sci. 12, 284–298 (1968).
Qin, J.-K. et al. Raman response and transport properties of tellurium atomic chains encapsulated in nanotubes. Nat. Electron. 3, 141–147 (2020).
Jin, K.-H. & Liu, F. 1D topological phases in transition-metal monochalcogenide nanowires. Nanoscale 12, 14661–14667 (2020).
Liu, S., Yin, H., Singh, D. J. & Liu, P.-F. Ta4SiTe4: a possible one-dimensional topological insulator. Phys. Rev. B 105, 195419 (2022).
Guo, H., Lin, Y. & Shen, S.-Q. Dimensional evolution between one- and two-dimensional topological phases. Phys. Rev. B 90, 085413 (2014).
Nadj-Perge, S., Frolov, S. M., Bakkers, E. P. A. M. & Kouwenhoven, L. P. Spin–orbit qubit in a semiconductor nanowire. Nature 468, 1084–1087 (2010).
Tokuyama, A., Moriya, A. & Nakayama, K. Development of Ar gas cluster ion beam system for surface preparation in angle-resolved photoemission spectroscopy. Rev. Sci. Instrum. 94, 023904 (2023).
Momma, K. & Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011).
El Azab, M., McLaughlin, C. R. & Champness, C. H. Preparation and characterization of tellurium surfaces. J. Cryst. Growth 28, 1–7 (1975).
Kitamura, M. et al. Development of a versatile micro-focused angle-resolved photoemission spectroscopy system with Kirkpatrick–Baez mirror optics. Rev. Sci. Instrum. 93, 033906 (2022).
Souma, S., Takayama, A., Sugawara, K., Sato, T. & Takahashi, T. Ultrahigh-resolution spin-resolved photoemission spectrometer with a mini Mott detector. Rev. Sci. Instrum. 81, 095101 (2010).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Wu, Q., Zhang, S., Song, H.-F., Troyer, M. & Soluyanov, A. A. WannierTools: an open-source software package for novel topological materials. Comput. Phys. Commun. 224, 405–416 (2018).
Mostofi, A. A. et al. wannier90: a tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 178, 685–699 (2008).
Aihara, Y., Hirayama, M. & Murakami, S. Anomalous dielectric response in insulators with the π Zak phase. Phys. Rev. Res. 2, 033224 (2020).
King-Smith, R. D. & Vanderbilt, D. Theory of polarization of crystalline solids. Phys. Rev. B 47, 1651–1654(1993).
Acknowledgements
This work was supported by JST-PRESTO (no. JPMJPR18L7), JST-CREST (no. JPMJCR18T1), Grant-in-Aid for Scientific Research (JSPS KAKENHI grant no. JP21H04435) and KEK-PF (proposal no. 2021S2-001). T.K. acknowledges support from GP-Spin at Tohoku University, JSPS (no. 23KJ0099) and JST-SPRING (no. JPMJSP2114).
Author information
Authors and Affiliations
Contributions
The research was conceived by K.N. and proceeded by discussion among K.N., A.T. and T.S.; A.T. and K. Segawa carried out the growth of single crystals; K.N. and A.T. performed the sample surface preparation; K.N., A.T., A.M., T.K., K. Sugawara, S.S., M.K., K.H., H.K., T.T. and T.S. performed the ARPES measurements; K.Y. and T.O. carried out the band-structure calculations; K.N. wrote the paper with input from all the authors. All the authors discussed the results and commented on the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Madhab Neupane and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Normal-emission ARPES data and estimation of inner potential.
a, Bulk and surface Brillouin zone (BZ) (dark blue and orange, respectively) for Te(0001). b, ARPES spectra measured in the normal-emission set up with varying photon energy (hν) from 46 eV to 100 eV. Blue dotted curve is a guide for the eyes to trace the band dispersion as a function of hν. c, ARPES intensity as a function of kz and binding energy, generated from the data in b by using the inner potential of 10.5 eV. Red curves indicate the bulk bands along the ΓA line obtained from the first-principles band calculations. d-j, Plots of peak position of the energy band traced by the blue dashed line in b, as a function of kz calculated with V0 = 9.0, 9.5, 10.0, 10.5, 11.0, 11.5, and 12.0 eV, respectively. Red curves are the results of numerical fittings with a cosine curve. Blue arrows highlight a finite phase shift δ. k, Plot of δ as a function of V0.
Extended Data Fig. 2 Band structure at naturally occurring edge on the surface.
a, Optical microscope image of Te(0001) surface. b, Plot of ARPES intensity at EF measured at the edge of naturally occurring terraces (indicated by a red circle in a) with 86-eV photons. The ARPES intensity of the in-gap states is marked by an orange arrow. c, Band dispersion measured along the yellow dashed line in b. Light blue curves are the calculated bulk band structure at kz = π.
Extended Data Fig. 3 Photon-energy dependent study of the in-gap states.
a-e, ARPES intensity plots measured at T = 30 K with hν = 76, 86, 96, 106, and 116 eV, respectively, along the \(\overline{{\rm{K}}\Gamma {\rm{KM}}}\) cut (same as the yellow dashed line in Fig. 2e). The in-gap states are marked by orange arrows.
Extended Data Fig. 4 Observation of in-gap states at room temperature.
a, b, ARPES intensity plots at EF measured at room temperature on a large terrace and at the crystal edge of Te(0001) surface, respectively, using 86-eV photons. c, Band dispersion measured along the yellow dashed line in b. Light blue curves are the calculated bulk band structure at kz = π. The ARPES intensity originating from the in-gap states is marked by orange arrow in b and c.
Extended Data Fig. 5 Orbital character of the in-gap states.
a, Orbital-resolved band structure. Red circles in a-c represent the contributions from the px, py, and pz orbitals, respectively, of Te atoms at the end of open Te chains (orange circles in d). The size of circle indicates the magnitude of contribution. d, Model crystal structure constructed to reproduce the band structure of the edge states, reproduced from Fig. 4f.
Extended Data Fig. 6 Site-selective dimerization.
a, b, Side and top views, respectively, of an artificial lattice in which the central Te helix is one-atom longer than others. The endpoints of the central and surrounding helices are indicated by magenta and green spheres, respectively. c, Same as b, but after site-selective dimerization of the helices indexed as A and L. d, e, Magnified view of the central Te helix of b and c, respectively. The definition of Te bond angle θ1 and θ2 is displayed.
Extended Data Fig. 7 Surface tilting effects.
a, b, Side and top views, respectively, of an artificial lattice to illustrate an example of tilted Te(0001) surfaces. The endpoint of each helix is shown by either orange, green, or magenta sphere. c, Reconstructed structure of b, obtained by taking into account the site-selective dimer formation. 1D arrays of open Te chains are highlighted by dashed orange rectangle.
Extended Data Fig. 8 AFM image of Te(0001) surface.
3D view of edges on the Te(0001) surface separated by a surface scratch, visualized by AFM measurements.
Extended Data Fig. 9 Calculated band structure of fully dimerized chains.
a, [0001] projection of the crystal structure which consists of full dimerization of Te chains. The unit cell is indicated by black line. b, Calculated band dispersions for the model shown in a.
Extended Data Fig. 10 Calculated band structure for a slanted surface with full dimerization.
a, b, Top and side views, respectively, of a fully dimerized \((01\bar{1}2)\) surface. c, Band dispersions calculated by assuming the slab displayed in a and b.
Supplementary information
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Nakayama, K., Tokuyama, A., Yamauchi, K. et al. Observation of edge states derived from topological helix chains. Nature 631, 54–59 (2024). https://doi.org/10.1038/s41586-024-07484-z
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41586-024-07484-z
This article is cited by
-
Efficient spin accumulation carried by slow relaxons in chiral tellurium
Nature Communications (2025)
-
Topological acoustofluidics
Nature Materials (2025)
-
Development of highly efficient and stable spin polarimeter for an undulator-based angle-resolved photoemission spectroscopy beamline
Journal of the Korean Physical Society (2025)