Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Permafrost slows Arctic riverbank erosion

Nature volume 634, pages 359–365 (2024)Cite this article

Subjects

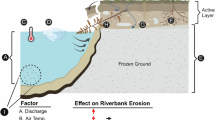
Abstract

The rate of river migration affects the stability of Arctic infrastructure and communities1,2 and regulates the fluxes of carbon3,4, nutrients5 and sediment6,7 to the oceans. However, predicting how the pace of river migration will change in a warming Arctic8 has so far been stymied by conflicting observations about whether permafrost9 primarily acts to slow10,11 or accelerate12,13 river migration. Here we develop new computational methods that enable the detection of riverbank erosion at length scales 5–10 times smaller than the pixel size in satellite imagery, an innovation that unlocks the ability to quantify erosion at the sub-monthly timescales when rivers undergo their largest variations in water temperature and flow. We use these high-frequency observations to constrain the extent to which erosion is limited by the thermal condition of melting the pore ice that cements bank sediment14, a requirement that will disappear when permafrost thaws, versus the mechanical condition of having sufficient flow to transport the sediment comprising the riverbanks, a condition experienced by all rivers15. Analysis of high-resolution data from the Koyukuk River, Alaska, shows that the presence of permafrost reduces erosion rates by 47%. Using our observations, we calibrate and validate a numerical model that can be applied to diverse Arctic rivers. The model predicts that full permafrost thaw may lead to a 30–100% increase in the migration rates of Arctic rivers.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Riverbank migration rates quantified for the approximately 450-km-long alluvial reach of the Koyukuk River near Huslia, Alaska.
Fig. 2: Spatial observations show that riverbank erosion rates are systematically slower in meanders that erode permafrost compared with those that erode unfrozen terrain.
Fig. 3: Model predictions for—and observations of—the temporal patterns of riverbank erosion.

Similar content being viewed by others

Data availability

The Sentinel-2 satellite images used to extract the 2016–2022 migration rates shown in Fig. 1 are freely available from the European Space Agency on data portals such as the Copernicus Open Access Hub (https://scihub.copernicus.eu/). The PlanetScope images used for the seasonal time-series analysis (Fig. 3) are available from Planet Labs (https://www.planet.com). The stream gauge data in Extended Data Fig. 2 are available from the United States Geological Survey (https://waterdata.usgs.gov/nwis). The permafrost map used in Fig. 2 and Extended Data Fig. 10 is from ref. 32 and is made available by the United States Geological Survey (https://www.sciencebase.gov/catalog/item/5602ab5ae4b03bc34f5448b4). Our spatial measurements of riverbank erosion from the Sentinel-2 and PlanetScope time-series analysis (Figs. 1–3) are packaged on the NSF Arctic Data Center68: https://doi.org/10.18739/A2HM52M6Q. Our field observations of permafrost presence/absence (Extended Data Fig. 10) from summer 2018 and fall 2022 are published on the ESS-DIVE repository67 (https://doi.org/10.15485/2204419).

Code availability

Our methodology for measuring sub-pixel bank erosion, as well as our workflow for channel extraction and the measurement of channel morphometrics (width, radius of curvature, longitudinal distance and so on) (Fig. 1), is available on the NSF Arctic Data Center68: https://doi.org/10.18739/A2HM52M6Q. The code is written in MATLAB.

References

  1. Hjort, J. et al. Degrading permafrost puts Arctic infrastructure at risk by mid-century. Nat. Commun. 9, 5147 (2018).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  2. Rowland, J. et al. Arctic landscapes in transition: responses to thawing permafrost. Eos 91, 229–230 (2010).

    Article  ADS  Google Scholar 

  3. Miner, K. R. et al. Permafrost carbon emissions in a changing Arctic. Nat. Rev. Earth Environ. 3, 55–67 (2022).

    Article  ADS  Google Scholar 

  4. Torres, M. A. et al. Model predictions of long-lived storage of organic carbon in river deposits. Earth Surf. Dyn. 5, 711–730 (2017).

    Article  ADS  Google Scholar 

  5. Terhaar, J., Lauerwald, R., Regnier, P., Gruber, N. & Bopp, L. Around one third of current Arctic Ocean primary production sustained by rivers and coastal erosion. Nat. Commun. 12, 169 (2021).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  6. Zhang, T. et al. Warming-driven erosion and sediment transport in cold regions. Nat. Rev. Earth Environ. 3, 832–851 (2022).

    Article  ADS  Google Scholar 

  7. Syvitski, J. et al. Earth’s sediment cycle during the Anthropocene. Nat. Rev. Earth Environ. 3, 179–196 (2022).

    Article  ADS  Google Scholar 

  8. Post, E. et al. The polar regions in a 2°C warmer world. Sci. Adv. 5, eaaw9883 (2019).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  9. Smith, S. L., O’Neill, H. B., Isaksen, K., Noetzli, J. & Romanovsky, V. E. The changing thermal state of permafrost. Nat. Rev. Earth Environ. 3, 10–23 (2022).

    Article  ADS  Google Scholar 

  10. Rowland, J. C. et al. Scale-dependent influence of permafrost on riverbank erosion rates. J. Geophys. Res. Earth Surf. 128, e2023JF007101 (2023).

    Article  ADS  Google Scholar 

  11. Piliouras, A., Lauzon, R. & Rowland, J. C. Unraveling the combined effects of ice and permafrost on Arctic delta morphodynamics. J. Geophys. Res. Earth Surf. 126, e2020JF005706 (2021).

    Article  ADS  Google Scholar 

  12. Ielpi, A., Lapôtre, M. G., Finotello, A. & Roy-Léveillée, P. Large sinuous rivers are slowing down in a warming Arctic. Nat. Clim. Change 13, 375–381 (2023).

    Article  ADS  Google Scholar 

  13. Kanevskiy, M. et al. Patterns and rates of riverbank erosion involving ice-rich permafrost (yedoma) in northern Alaska. Geomorphology 253, 370–384 (2016).

    Article  ADS  Google Scholar 

  14. Douglas, M. M., Dunne, K. B. & Lamb, M. P. Sediment entrainment and slump blocks limit permafrost riverbank erosion. Geophys. Res. Lett. 50, e2023GL102974 (2023).

    Article  ADS  Google Scholar 

  15. Phillips, C. B. et al. Threshold constraints on the size, shape and stability of alluvial rivers. Nat. Rev. Earth Environ. 3, 406–419 (2022).

    Article  ADS  Google Scholar 

  16. Douglas, M. M. et al. Organic carbon burial by river meandering partially offsets bank erosion carbon fluxes in a discontinuous permafrost floodplain. Earth Surf. Dyn. 10, 421–435 (2022).

    Article  ADS  Google Scholar 

  17. Striegl, R. G., Dornblaser, M. M., Aiken, G. R., Wickland, K. P. & Raymond, P. A. et al. Carbon export and cycling by the Yukon, Tanana, and Porcupine rivers, Alaska, 2001–2005. Water Resourc. Res. 43, W02411 (2007).

    Article  ADS  Google Scholar 

  18. Teufel, B. & Sushama, L. Abrupt changes across the Arctic permafrost region endanger northern development. Nat. Clim. Change 9, 858–862 (2019).

    Article  ADS  Google Scholar 

  19. Chadburn, S. et al. An observation-based constraint on permafrost loss as a function of global warming. Nat. Clim. Change 7, 340–344 (2017).

    Article  ADS  Google Scholar 

  20. Langhorst, T. & Pavelsky, T. Global observations of riverbank erosion and accretion from Landsat imagery. J. Geophys. Res. Earth Surf. 128, e2022JF006774 (2023).

    Article  ADS  Google Scholar 

  21. Chassiot, L., Lajeunesse, P. & Bernier, J.-F. Riverbank erosion in cold environments: review and outlook. Earth-Sci. Rev. 207, 103231 (2020).

    Article  Google Scholar 

  22. Constantine, C. R., Dunne, T. & Hanson, G. J. Examining the physical meaning of the bank erosion coefficient used in meander migration modeling. Geomorphology 106, 242–252 (2009).

    Article  ADS  Google Scholar 

  23. Constantine, J. A., Dunne, T., Ahmed, J., Legleiter, C. & Lazarus, E. D. Sediment supply as a driver of river meandering and floodplain evolution in the Amazon Basin. Nat. Geosci. 7, 899–903 (2014).

    Article  ADS  CAS  Google Scholar 

  24. Sylvester, Z., Durkin, P. & Covault, J. A. High curvatures drive river meandering. Geology 47, 263–266 (2019).

    Article  ADS  Google Scholar 

  25. Feng, D. et al. Recent changes to Arctic river discharge. Nat. Commun. 12, 6917 (2021).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  26. Costard, F. et al. Impact of the global warming on the fluvial thermal erosion over the Lena River in Central Siberia. Geophys. Res. Lett. 34, L14501 (2007).

    Article  ADS  Google Scholar 

  27. Costard, F., Dupeyrat, L., Gautier, E. & Carey-Gailhardis, E. Fluvial thermal erosion investigations along a rapidly eroding river bank: application to the Lena River (central Siberia). Earth Surf. Process. Landf. 28, 1349–1359 (2003).

    Article  ADS  Google Scholar 

  28. Scott, K. M. Effects of permafrost on stream channel behavior in Arctic Alaska. Professional Paper 1068. United States Geological Survey (1978).

  29. Rowland, J. C. et al. A morphology independent methodology for quantifying planview river change and characteristics from remotely sensed imagery. Remote Sens. Environ. 184, 212–228 (2016).

    Article  ADS  Google Scholar 

  30. Langhorst, T. & Pavelsky, T. M. Global observations of riverbank erosion and accretion from Landsat imagery. J. Geophys. Res. Earth Surf. 128, e2022JF006774 (2023).

    Article  ADS  Google Scholar 

  31. Leprince, S., Barbot, S., Ayoub, F. & Avouac, J.-P. Automatic and precise orthorectification, coregistration, and subpixel correlation of satellite images, application to ground deformation measurements. IEEE Trans. Geosci. Remote Sens. 45, 1529–1558 (2007).

    Article  ADS  Google Scholar 

  32. Pastick, N. J. et al. Distribution of near-surface permafrost in Alaska: estimates of present and future conditions. Remote Sens. Environ. 168, 301–315 (2015).

    Article  ADS  Google Scholar 

  33. Douglas, M. M. et al. Permafrost formation in a meandering river floodplain. AGU Adv. 5, e2024AV001175 (2024).

  34. Finnegan, N. J. & Dietrich, W. E. Episodic bedrock strath terrace formation due to meander migration and cutoff. Geology 39, 143–146 (2011).

    Article  ADS  Google Scholar 

  35. Douglas, M. M., Miller, K. L., Schmeer, M. N. & Lamb, M. P. Ablation-limited erosion rates of permafrost riverbanks. J. Geophys. Res. Earth Surf. 128, e2023JF007098 (2023).

    Article  ADS  Google Scholar 

  36. Parker, G. Self-formed straight rivers with equilibrium banks and mobile bed. Part 2. The gravel river. J. Fluid Mech. 89, 127–146 (1978).

    Article  ADS  Google Scholar 

  37. Dunne, K. B. & Jerolmack, D. J. What sets river width? Sci. Adv. 6, eabc1505 (2020).

    Article  ADS  PubMed  PubMed Central  Google Scholar 

  38. Partheniades, E. Erosion and deposition of cohesive soils. J. Hydraul. Div. 91, 105–139 (1965).

    Article  Google Scholar 

  39. Howard, A. D. & Knutson, T. R. Sufficient conditions for river meandering: a simulation approach. Water Resour. Res. 20, 1659–1667 (1984).

    Article  ADS  Google Scholar 

  40. Furbish, D. J. River-bend curvature and migration: how are they related? Geology 16, 752–755 (1988).

    Article  ADS  Google Scholar 

  41. Vanoni, V. A. & Brooks, N. H. Laboratory Studies of the Roughness and Suspended Load of Alluvial Streams (California Institute of Technology Sedimentation Laboratory, 1957).

  42. Kean, J. W. & Smith, J. D. in Riparian Vegetation and Fluvial Geomorphology Vol. 8 (eds Bennett, S. J. & Simon, A.) 237–252 (American Geophysical Union, 2004).

  43. Li, T., Venditti, J. G., Rennie, C. D. & Nelson, P. A. Bed and bank stress partitioning in bedrock rivers. J. Geophys. Res. Earth Surf. 127, e2021JF006360 (2022).

    Article  ADS  Google Scholar 

  44. Ferguson, R. I., Hardy, R. J. & Hodge, R. A. Flow resistance and hydraulic geometry in bedrock rivers with multiple roughness length scales. Earth Surf. Process. Landf. 44, 2437–2449 (2019).

    Article  ADS  Google Scholar 

  45. Douglas, M. M. & Lamb, M. P. A model for thaw and erosion of permafrost riverbanks. J. Geophys. Res. Earth Surf. 129, e2023JF007452 (2024).

    Article  ADS  Google Scholar 

  46. Leprince, S. Monitoring Earth Surface Dynamics With Optical Imagery. PhD thesis, California Institute of Technology (2008).

  47. Altena, B. & Leinss, S. Improved surface displacement estimation through stacking cross-correlation spectra from multi-channel imagery. Sci. Remote Sens. 6, 100070 (2022).

    Article  Google Scholar 

  48. Parker, G. et al. A new framework for modeling the migration of meandering rivers. Earth Surf. Process. Landf. 36, 70–86 (2011).

    Article  ADS  Google Scholar 

  49. Ikeda, S., Parker, G. & Sawai, K. Bend theory of river meanders. Part 1. Linear development. J. Fluid Mech. 112, 363–377 (1981).

    Article  ADS  Google Scholar 

  50. Savitzky, A. & Golay, M. J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 36, 1627–1639 (1964).

    Article  ADS  CAS  Google Scholar 

  51. Schoene, B. et al. U-Pb constraints on pulsed eruption of the Deccan Traps across the end-Cretaceous mass extinction. Science 363, 862–866 (2019).

    Article  ADS  CAS  PubMed  Google Scholar 

  52. Keller, C. B. Chron.jl: a Bayesian framework for integrated eruption age and age-depth modelling. OSF (Open Science Framework) https://doi.org/10.17605/OSF.IO/TQX3F (2018).

  53. Schoene, B., Eddy, M. P., Keller, C. B. & Samperton, K. M. An evaluation of Deccan Traps eruption rates using geochronologic data. Geochronology 3, 181–198 (2021).

    Article  ADS  CAS  Google Scholar 

  54. Zhang, T. et al. A Bayesian framework for subsidence modeling in sedimentary basins: a case study of the Tonian Akademikerbreen Group of Svalbard, Norway. Earth Planet. Sci. Lett. 620, 118317 (2023).

    Article  CAS  Google Scholar 

  55. Fisk, H. N. Geological Investigation of the Alluvial Valley of the Lower Mississippi River (U.S. Army Corps of Engineers, 1944).

  56. Leopold, L. B. & Wolman, M. G. River meanders. Geol. Soc. Am. Bull. 71, 769–793 (1960).

    Article  ADS  Google Scholar 

  57. Hickin, E. J. & Nanson, G. C. The character of channel migration on the Beatton River, northeast British Columbia, Canada. Geol. Soc. Am. Bull. 86, 487–494 (1975).

    Article  ADS  Google Scholar 

  58. Dietrich, W. E., Smith, J. D. & Dunne, T. Flow and sediment transport in a sand bedded meander. J. Geol. 87, 305–315 (1979).

    Article  ADS  Google Scholar 

  59. Hooke, R. L. B. Distribution of sediment transport and shear stress in a meander bend. J. Geol. 83, 543–565 (1975).

    Article  ADS  Google Scholar 

  60. Donovan, M., Belmont, P. & Sylvester, Z. Evaluating the relationship between meander-bend curvature, sediment supply, and migration rates. J. Geophys. Res. Earth Surf. 126, e2020JF006058 (2021).

    Article  ADS  Google Scholar 

  61. Bagnold, R. A. Some Aspects of the Shape of River Meanders (US Government Printing Office, 1960).

  62. Eke, E., Parker, G. & Shimizu, Y. Numerical modeling of erosional and depositional bank processes in migrating river bends with self-formed width: morphodynamics of bar push and bank pull. J. Geophys. Res. Earth Surf. 119, 1455–1483 (2014).

    Article  ADS  Google Scholar 

  63. Nicoll, T. J. & Hickin, E. J. Planform geometry and channel migration of confined meandering rivers on the Canadian prairies. Geomorphology 116, 37–47 (2010).

    Article  ADS  Google Scholar 

  64. Hudson, P. F. & Kesel, R. H. Channel migration and meander-bend curvature in the lower Mississippi River prior to major human modification. Geology 28, 531–534 (2000).

    Article  ADS  Google Scholar 

  65. Finotello, A. et al. Field migration rates of tidal meanders recapitulate fluvial morphodynamics. Proc. Natl Acad. Sci. 115, 1463–1468 (2018).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  66. Hooke, J. River meander behaviour and instability: a framework for analysis. Trans. Inst. Br. Geogr. 28, 238–253 (2003).

    Article  Google Scholar 

  67. Douglas, M. et al. Geomorphic mapping and permafrost occurrence on the Koyukuk River floodplain near Huslia, Alaska (ESS-DIVE dataset) (2023).

  68. Geyman, E., Avouac, J.-P., Douglas, M. & Lamb, M. Resolving the spatial and seasonal pattern of riverbank erosion on the Koyukuk River, Alaska, 2016–2022. Arctic Data Center (2024).

  69. Beltaos, S., Carter, T., Rowsell, R. & DePalma, S. G. Erosion potential of dynamic ice breakup in Lower Athabasca River. Part I: field measurements and initial quantification. Cold Reg. Sci. Technol. 149, 16–28 (2018).

    Article  Google Scholar 

  70. Vandermause, R., Harvey, M., Zevenbergen, L. & Ettema, R. River-ice effects on bank erosion along the middle segment of the Susitna river, Alaska. Cold Reg. Sci. Technol. 185, 103239 (2021).

    Article  Google Scholar 

  71. Milburn, D. & Prowse, T. D. The effect of river-ice break-up on suspended sediment and select trace-element fluxes: paper presented at the 10th Northern Res. Basin Symposium (Svalbard, Norway – 28 Aug./3 Sept. 1994). Hydrol. Res. 27, 69–84 (1996).

    Article  CAS  Google Scholar 

  72. Ettema, R. Review of alluvial-channel responses to river ice. J. Cold Reg. Eng. 16, 191–217 (2002).

    Article  Google Scholar 

  73. Costard, F., Gautier, E., Fedorov, A., Konstantinov, P. & Dupeyrat, L. An assessment of the erosion potential of the fluvial thermal process during ice breakups of the Lena River (Siberia). Permafr. Periglac. Process. 25, 162–171 (2014).

    Article  Google Scholar 

  74. Lininger, K., Wohl, E., Rose, J. & Leisz, S. Significant floodplain soil organic carbon storage along a large high-latitude river and its tributaries. Geophys. Res. Lett. 46, 2121–2129 (2019).

    Article  ADS  CAS  Google Scholar 

  75. Lunardini, V. J., Zisson, J. R. & Yen, Y. C. Experimental Determination of Heat Transfer Coefficients in Water Flowing over a Horizontal Ice Sheet (US Army Corps of Engineers, Cold Regions Research & Engineering Laboratory, 1986).

Download references

Acknowledgements

We thank the Huslia Tribal Council for river and land access and S. Huffman and the Yukon River Inter-Tribal Watershed Council for field and logistical support. We also thank J. Anadu, R. Blankenship, K. Dunne, W. Fischer, Y. Ke, H. Dion-Kirschner, J. Magyar, E. Mutter, J. Nghiem, J. Reahl, R. Rugama-Montenegro, E. Seelen, I. Smith and J. West for help in the field and for fruitful discussions. Planet Labs provided the high-resolution PlanetScope imagery through their Education and Research Program. This work was supported by NSF Award 2127442, NSF Award 2031532, and Caltech’s Resnick Sustainability Institute. E.C.G. thanks the NSF Graduate Research Fellowships Program and the Fannie and John Hertz Foundation.

Author information

Authors and Affiliations

  1. Division of Geological and Planetary Sciences, California Institute of Technology, Pasadena, CA, USA

    Emily C. Geyman, Madison M. Douglas, Jean-Philippe Avouac & Michael P. Lamb

  2. Department of Earth, Atmospheric, and Planetary Sciences, Massachusetts Institute of Technology, Cambridge, MA, USA

    Madison M. Douglas

Authors
  1. Emily C. Geyman
    View author publications

    Search author on:PubMed Google Scholar

  2. Madison M. Douglas
    View author publications

    Search author on:PubMed Google Scholar

  3. Jean-Philippe Avouac
    View author publications

    Search author on:PubMed Google Scholar

  4. Michael P. Lamb
    View author publications

    Search author on:PubMed Google Scholar

Contributions

E.C.G. and M.P.L. designed the study. M.M.D. and M.P.L. developed the early thermomechanical model. J.-P.A. advised the sub-pixel methodology. E.C.G. developed the sub-pixel methodology, performed the analysis and wrote the manuscript, with input from M.M.D., J.-P.A. and M.P.L.

Corresponding author

Correspondence to Emily C. Geyman.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature thanks Evan Dethier, Efi Foufoula-Georgiou and Zoltan Sylvester for their contribution to the peer review of this work. Peer reviewer reports are available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data figures and tables

Extended Data Fig. 1 Discharge and water temperature seasonality on the Koyukuk River (Alaska) and theoretical predictions for the timing of riverbank erosion.

a, Discharge climatology for the Koyukuk River at Hughes (66.04696° N, 154.26097° W) based on data from the USGS streamflow station during the period 1962–1981 (Extended Data Fig. 7a). Note that 1 ft3/s is equal to approximately 0.028 m3/s. Discharge peaks during the spring freshet in late May to early June. Some years have a second discharge peak associated with August rains (Extended Data Figs. 3 and 7a). The Koyukuk River maintains very low discharge from late October to mid-May, when the surface of the river is frozen. b, Average water temperature time series from the USGS gauge at Pilot Station on the Yukon River (61.93369° N, 162.88293° W). The USGS gauge at Hughes does not record water temperature, which is why we rely on the Pilot Station temperature record. However, comparison of water temperatures measured by HOBO loggers deployed on the Koyukuk River near Huslia during the summers of 2022 and 2023 show that the water temperature at Pilot Station is a good proxy for the water temperature on the Koyukuk River. Water temperatures approach 0 °C during the river-ice ‘break-up’ and ‘freeze-up’ periods, and peak in mid-July, at a time when the water discharge approaches its summertime low (a). c–e, Theoretical predictions for the sub-seasonal patterns of riverbank erosion under the endmember scenarios that erosion is controlled by: ice gouging during break-up69,70,71,72 (c), the thawing of pore-ice in frozen bank sediments14,26,27,73 (d) and the ability for flowing river water to entrain bank sediment14,36,37,38 (e). The time series in c is an illustrative cartoon. The break-up period in May is probably the time of greatest erosive action from ice21, although the freeze-up period in October can proceed in fits and starts, during which thin ice lenses flow downstream and could erode thawed riverbanks. The uncertainty envelopes in d and e propagate the discharge and water temperature variability in a and b using Monte Carlo simulations.

Extended Data Fig. 2 Illustration and justification for our method of estimating discharge on the Koyukuk River (which is missing gauge data during our study period from 2016 to 2022) based on the discharge time series from nearby rivers.

a–e, Discharge records from USGS stream gauges at Hughes (66.04696° N, 154.26097° W) (a–e), Pilot Station (61.93369° N, 162.88293° W) (a), Nenana (64.56494° N, 149.09400° W) (b), Stevens Village (65.87510° N, 149.72035° W) (c), Eagle (64.78917° N, 141.20009° W) (d), and Fairbanks (64.79234° N, 147.84131° W) (e). Note that 1 ft3/s is equal to approximately 0.028 m3/s. The discharge data for the Koyukuk River at Hughes are shown in brown and the discharge data from all other stations are shown in green. f–j, A zoom-in of the period 1977–1982, when all six stations were recording discharge data. Note the similarity in the hydrographs between the stations. We ask: can we use the historical period of overlap (f–j) to train a model that infers the discharge on the Koyukuk River given the hydrographs recorded at nearby stations? k, Consider the specific case of the streamflow recorded at Hughes, Pilot Station and Stevens Village. The Koyukuk River carries roughly 20% of the streamflow observed on the Yukon River at Stevens Village (c,h). Thus, the difference in discharge observed at Stevens Village versus Pilot Station (that is, before and after the confluence with the Koyukuk River, respectively) should encode information about the discharge from the Koyukuk River, modulated by a characteristic convolutional smoothing of the hydrograph from upstream to downstream. l, We use a simple neural network to infer the hydrograph from the Koyukuk River (which is not directly observed during our study period from 2016–2022) based on the hydrographs of the Yukon River at Stevens Village and Pilot Station (which have continuous observational records from 2016 to 2022). We train the neural network using the period of overlap when all three stations were collecting data from 1977 to 1982 (Extended Data Fig. 3).

Extended Data Fig. 3 Training and implementation of our neural network used to infer the ‘missing’ discharge time series on the Koyukuk River based on the discharge records at Stevens Village and Pilot Station on the Yukon River (before and after the confluence with the Koyukuk River)—see Extended Data Fig. 2.

a–e, The neural network is trained using periods of overlap in the historical record when all three USGS streamflow stations were active. In a–e, the R2 values represent the model performance evaluated using leave-one-out cross-validation. The neural network predicts the historical discharge time series with a mean R2 of 0.82. f–j, Implementation of the neural network for estimating the Koyukuk River discharge records during the period 2017–2021. These datasets are used to make model predictions for the seasonal and interannual patterns of riverbank erosion under the thaw-limited, entrainment-limited and combined scenarios (Extended Data Fig. 4).

Extended Data Fig. 4 Time series for quantifying annual erosion rates.

a,b, Power-law regressions relating the water discharge, Qw, to the average flow depth (H) (a) and average flow velocity (U) (b) for the USGS station at Hughes. Each data point represents a field measurement from the USGS (mostly from the period 1962–1981). c, In situ water temperature observations from Pilot Station on the Yukon River. d, Water discharge time series for the Koyukuk River estimated from the neural network in Extended Data Fig. 3. e,f, Time series of average flow depth (H) and average flow velocity (U) constructed from the discharge dataset in d and the power-law fits in a and b. g, Predicted patterns of thaw-limited and entrainment-limited erosion based on equations (3)–(6) and the H and U time series in e and f. h, The minimum of the thaw-limited and entrainment-limited erosion curves in g. In g and h, the y axis gives the instantaneous erosion rate (that is, the total annual erosion that would occur if that rate were sustained for a full 365-day period). i–k, The integrated areas under the erosion rate curves (g and h) for thaw-limited (i), entrainment-limited (j) and combined (k) erosion scenarios. l, The observed erosion rates for 2017–2021. Note that the model parameters in equations (3)–(6) are optimized separately for each scenario (i–k) to have the interannual erosion fingerprint best match the observations (l) (see Extended Data Fig. 1). Even after optimization, the thaw-limited and entrainment-limited endmembers can only replicate the interannual pattern of erosion with R2 of 0.44 and 0.57, respectively. The combined thaw and entrainment scenario reproduces the interannual pattern with R2 = 0.85. To account for the fact that the thaw-only, entrainment-only and combined thaw and entrainment models have different numbers of independent parameters (1, 2 and 3, respectively), we also compute the adjusted R2 value (see equation (15)). The \({R}_{{\rm{adj}}}^{2}\) metric includes a penalty for models with more parameters, yet it still supports the conclusion that the combined thaw and entrainment model best explains the data.

Extended Data Fig. 5 Simulations for how the reach-averaged riverbank erosion rates for the Koyukuk River may respond to changes in the total water discharge, the discharge seasonality, the water temperature, and the permafrost abundance in the riverbanks.

We use the combined thaw-limited and entrainment-limited erosion model (Fig. 3), calibrated using our observations for the seasonal and interannual patterns of bank erosion, to explore changes in erosion rates in response to perturbations in total water discharge (Qw), discharge seasonality, and water temperature (Tw). Note that our perturbations to the discharge seasonality involve reallocating 0–30% of the water discharge from the first 30 days of ice-free conditions (mid-May to mid-June on the Koyukuk River) to the mid-summer (in this case, to the month of August). This experiment simulates reduced springtime discharge as a result of a smaller snowpack, compensated by increasing summertime rain8. Because we lack robust constraints on whether or how the ‘flashiness’ of the Koyukuk River hydrograph will change, we reallocate the seasonal discharge through simple linear scalings of the historical discharge records (Extended Data Fig. 2). The numbers in bold indicate the reach-averaged bank erosion rates in metres per year and the numbers in parentheses indicate the percent change relative to the modern (2016–2022) erosion rates.

Extended Data Fig. 6 Methodology for measuring sub-pixel erosion along riverbanks.

a, An illustration of the workflow for the sub-pixel detection of riverbank erosion. b,c, An example of the two Sentinel-2 images used to compute the migration of the Koyukuk River (2016–2022) in Extended Data Fig. 9. The crops in b and c show a region of the Koyukuk River near Huslia (65.6966° N, 156.3824° W). Note that the river stage and sediment load are higher on 30 August 2016 compared with 13 July 2022, causing the river colour (RGB values) and the position of the land–water boundary to be different in the two images. We want to make sure that our algorithm records the net migration of the river as a result of bank erosion, rather than the variable exposure of sand on the riverbanks resulting from rising and falling river stage. To do so, we transform the multispectral satellite image to the dimensionless NDVI band ratio (equation (18)). The NDVI accentuates the spectral difference between the river water and the vegetated floodplain while collapsing the spectral difference between unvegetated sand and river water. The result is that the NDVI image is relatively insensitive to changes in water level (which expose or submerge unvegetated bars). Next, we extract an n × n-pixel chip, centred at the bank edge for the location of interest, from the image acquired at time 1. We extract an n × n-pixel chip at the same location in the image acquired at time 2. We use Fourier methods to take the 2D cross-correlation of the two image chips. The 2D cross-correlation spectrum, which we upsample by a factor of 10, peaks at a (Δx, Δy) value that records the estimated riverbank displacement between time 1 and time 2. Note that, given the relatively linear bank geometry (at least on the scale of the n × n-pixel chips), the cross-correlation spectrum has a ridge-like geometry rather than a sharp peak. Thus, when searching for the maximum in the 2D cross-correlation spectrum, we search along a vector that is perpendicular to the orientation of the riverbank (and therefore perpendicular to the ridge in the cross-correlation spectrum). d,e, Illustration of how we perform the methodology described in a for every position along the 450-km reach of the Koyukuk River shown in Fig. 1b.

Extended Data Fig. 7 A synthetic dataset to illustrate our method of reconstructing erosion rates from pairwise bank displacement observations.

a, Continuous discharge time series for the Koyukuk River from the USGS station at Hughes (1961–1982). b, Average annual discharge cycle based on the data in a. c, A simple synthetic time series for erosion rate based on equation (6) (the entrainment-limited endmember). The ‘instantaneous’ erosion rate gives the total annual erosion that would occur if that erosion rate were sustained for a 365-day period. The grey lines depict the times for which we have PlanetScope images (see Supplementary Table 1). d, The cumulative erosion from the synthetic curve in d. e, A pairwise displacement matrix computed from the synthetic cumulative erosion curve in d. f, An example real (noisy) displacement record. g, Stacking and bracketing of the displacement matrix leads to less noisy cumulative displacement records. Stacking refers to averaging the differential displacement time series along each column of the matrix in e. Bracketing refers to computing the cumulative displacement from every second column, every third column, every fourth column and so on. Stacking (averaging over the rows) makes the cumulative displacement estimates less sensitive to errors in the co-registration of the template image (rows of E(x, y)), whereas bracketing (skipping columns) makes the cumulative displacement estimates less sensitive to errors in the co-registration of the search image (columns of E(x, y)). h,i, Remaining noise in the stacked and bracketed cumulative erosion record (g) is reduced by imposing the constraint that the cumulative displacement time series should be a monotonic function of time; in most cases, an eroding riverbank should not switch from eroding to accreting over the course of our approximately 6-year analysis. Thus, temporary back-stepping of the bank position (h) is probably an error. i, We use MCMC to construct the most probable monotonic path through the cumulative displacement time series. j, Differentiating the record in i with respect to time yields an estimate for the instantaneous erosion rate. The green curve shows the synthetic curve used to generate the displacement matrix (e) and the grey curve gives the reconstructed erosion rate (shown as a stair-step plot rather than a continuous curve because our temporal observations are limited to the roughly ten cloud-free PlanetScope mosaics each year (Supplementary Table 1).

Extended Data Fig. 8 Representative field photos of the Koyukuk River near Huslia (65.689° N, 156.381° W).

a, Scroll bars are arcuate traces of the river’s former position recorded in the floodplain landscape. b, The inner bend of a channel (point bar) is accretionary, whereas its outer bend (cut bank) is erosional. c, A zoom-in on an erosional permafrost cut bank.

Extended Data Fig. 9 Spatial patterns of riverbank erosion on the Koyukuk River.

This figure is similar to Fig. 1 but it shows the river migration rate as a function of both the local normalized river curvature (W/R, in which W is the river width (m) and R is the local radius of curvature of the channel (m)) (e–g) and the lag-adjusted normalized curvature, which is given by equation (26) (h–l). Note that the migration rate saturates at high values of local curvature in c–f, giving the curvature versus migration rate curves a sigmoidal shape. By contrast, the migration rate is a linear function of the lag-adjusted normalized curvature24. Notice that the y-axis scale in k and l is two times the scale in h–j. In other words, after the confluence of the two threads of the Koyukuk River at the location indicated by the black arrow in b, the curvature-normalized migration rate increases by a factor of 2. As in Fig. 1, the migration rates were measured by applying our sub-pixel offset algorithm to a pair of Sentinel-2 images from 30 August 2016 and 13 July 2022. Here, as in Fig. 1, we quantify the migration rate using the displacement observed on the erosional side of the river (see Fig. 1e).

Extended Data Fig. 10 Field validation of the near-surface permafrost map.

a, Probability of near-surface (≤1 m depth) permafrost estimated by Pastick et al.32. b, Zoom-in to our area of field observations, in which we collected n = 176 permafrost probe measurements in July 2018 (n = 137), June 2022 (n = 2) and October 2022 (n = 37). Blue dots indicate permafrost detected and red dots indicate no permafrost detected. c, A comparison between our permafrost ground-truth observations (b) and the permafrost probability estimates from Pastick et al.32 (an Alaska-wide permafrost map, calibrated using n = 16,786 statewide observations of near-surface permafrost, but no observations in the region shown in b). d, We explore the accuracy of the Pastick et al.32 permafrost map for the Koyukuk region based on applying a simple classification threshold (that is, classifying all pixels with a reported permafrost probability below the threshold as not permafrost and all pixels with a reported permafrost probability above the threshold as permafrost). We sweep through all possible threshold values, from 0% to 100%, and compute the true positive and true negative rates, as well as the total accuracy. e, The threshold value of 40% yields the highest total classification accuracy. The true-negative, false-negative, false-positive and true-positive values for this classification are shown in the confusion matrix in e. The satellite imagery in b is from Bing Maps Aerial, reprinted with permission from Microsoft Corporation.

Extended Data Table 1 Physical constants and parameters used for equations (3)–(6)
Full size table

Supplementary information

Supplementary Information

Supplementary Information, including Supplementary Figs. 1–11, Supplementary Tables 1 and 2 and Supplementary References.

Peer Review File

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Geyman, E.C., Douglas, M.M., Avouac, JP. et al. Permafrost slows Arctic riverbank erosion. Nature 634, 359–365 (2024). https://doi.org/10.1038/s41586-024-07978-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41586-024-07978-w

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing