Abstract
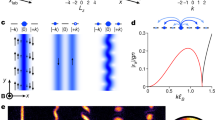
A key concept proposed by Landau to explain superfluid liquid helium is the elementary excitation of quantum particles called rotons1,2,3,4,5,6,7,8. The irregular arrangement of atoms in a liquid leads to the aperiodic dispersion of rotons, which played a pivotal role in understanding fractional quantum Hall liquids (magneto-rotons)9,10 and the supersolidity of Bose–Einstein condensates11,12,13. Even for a two-dimensional electron or dipole liquid, in the absence of a magnetic field, the repulsive interactions have been predicted to form a roton minimum14,15,16,17,18,19, which can be used to trace the transition to Wigner crystals20,21,22,23,24 and superconductivity25,26,27, although this has not yet been observed. Here, we report the observation of such electronic rotons in a two-dimensional dipole liquid of alkali-metal ions donating electrons to surface layers of black phosphorus. Our data reveal the striking aperiodic dispersion of rotons, which is characterized by a local minimum of energy at finite momentum. As the density of dipoles decreases so that interactions dominate over the kinetic energy, the roton gap reduces to 0, as in a crystal, signalling Wigner crystallization. Our model shows the importance of short-range order arising from repulsion between dipoles, which can be viewed as the formation of Wigner crystallites (bubbles or stripes) floating in the sea of a Fermi liquid. Our results reveal that the primary origin of electronic rotons (and the pseudogap) is strong correlations.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
Source Data are provided with this paper. Any other data that support the findings of this paper are available from the corresponding author on request.
References
Landau, L. Theory of the superfluidity of helium ii. Phys. Rev. 60, 356–358 (1941).
Landau, L. On the theory of superfluidity of helium ii. J. Phys. 11, 91–92 (1947).
Feynman, R. P. & Cohen, M. Energy spectrum of the excitations in liquid helium. Phys. Rev. 102, 1189–1204 (1956).
Henshaw, D. G. & Woods, A. D. B. Modes of atomic motions in liquid helium by inelastic scattering of neutrons. Phys. Rev. 121, 1266–1274 (1961).
Godfrin, H. et al. Observation of a roton collective mode in a two-dimensional Fermi liquid. Nature 483, 576–579 (2012).
Donnelly, R. Rotons: a low-temperature puzzle. Phys. World 10, 25–30 (1997).
Nozières, P. Is the roton in superfluid 4He the ghost of a Bragg spot? J. Low Temp. Phys. 137, 45–67 (2004).
Bobrov, V., Trigger, S. & Litinski, D. Universality of the phonon-roton spectrum in liquids and superfluidity of 4He. Z. Naturforsch. A 71, 565–575 (2016).
Girvin, S. M., MacDonald, A. H. & Platzman, P. M. Magneto-roton theory of collective excitations in the fractional quantum Hall effect. Phys. Rev. B 33, 2481–2494 (1986).
Kukushkin, I. V., Smet, J. H., Scarola, V. W., Umansky, V. & von Klitzing, K. Dispersion of the excitations of fractional quantum Hall states. Science 324, 1044–1047 (2009).
Mottl, R. et al. Roton-type mode softening in a quantum gas with cavity-mediated long-range interactions. Science 336, 1570–1573 (2012).
Chomaz, L. et al. Observation of roton mode population in a dipolar quantum gas. Nat. Phys. 14, 442–446 (2018).
Mukherjee, B. et al. Crystallization of bosonic quantum Hall states in a rotating quantum gas. Nature 601, 58–62 (2022).
Apaja, V., Halinen, J., Halonen, V., Krotscheck, E. & Saarela, M. Charged-boson fluid in two and three dimensions. Phys. Rev. B 55, 12925–12945 (1997).
De Palo, S., Conti, S. & Moroni, S. Monte Carlo simulations of two-dimensional charged bosons. Phys. Rev. B 69, 035109 (2004).
Kalman, G. J., Hartmann, P., Golden, K. I., Filinov, A. & Donkó, Z. Correlational origin of the roton minimum. Europhys. Lett. 90, 55002 (2010).
Kalman, G. J., Kyrkos, S., Golden, K. I., Hartmann, P. & Donkó, Z. The roton minimum: is it a general feature of strongly correlated liquids? Contrib. Plasma Phys. 52, 219–223 (2012).
Dorheim, T., Moldabekov, Z., Vorberger, J., Kählert, H. & Bonitz, M. Electronic pair alignment and roton feature in the warm dense electron gas. Commun. Phys. 5, 304 (2022).
Lu, H., Chen, B.-B., Wu, H.-Q., Sun, K. & Meng, Z. Y. Thermodynamic response and neutral excitations in integer and fractional quantum anomalous Hall states emerging from correlated flat bands. Phys. Rev. Lett. 132, 236502 (2024).
Wigner, E. On the interaction of electrons in metals. Phys. Rev. 46, 1002–1010 (1934).
Tanatar, B. & Ceperley, D. M. Ground state of the two-dimensional electron gas. Phys. Rev. B 39, 5005–5016 (1989).
De Palo, S., Rapisarda, F. & Senatore, G. Excitonic condensation in a symmetric electron-hole bilayer. Phys. Rev. Lett. 88, 206401 (2002).
Spivak, B. & Kivelson, S. A. Phase intermediate between a two-dimensional electron liquid and Wigner crystal. Phys. Rev. B 70, 155114 (2004).
Hartmann, P., Donkó, Z. & Kalman, G. J. Structure and phase diagram of strongly-coupled bipolar charged-particle bilayers. Europhys. Lett. 72, 396–402 (2005).
Lozovik, Y. E. & Yudson, V. I. A new mechanism for superconductivity: pairing between spatially separated electrons and holes. Sov. Phys. JETP 44, 738–753 (1976).
Balatsky, A. V., Joglekar, Y. N. & Littlewood, P. B. Dipolar superfluidity in electron-hole bilayer systems. Phys. Rev. Lett. 93, 266801 (2004).
Joglekar, Y. N., Balatsky, A, V. & Das Sarma, S. Wigner supersolid of excitons in electron-hole bilayers. Phys. Rev. B 74, 233302 (2006).
Glyde, H. R. & Griffin, A. Zero sound and atomiclike excitations: the nature of phonons and rotons in liquid 4He. Phys. Rev. Lett. 65, 1454–1457 (1990).
Filinov, A. & Bonitz, M. Collective and single-particle excitations in two-dimensional dipolar Bose gases. Phys. Rev. A 86, 063628 (2012).
De Dycker, E. & Phariseau, P. On the LCAO-method for disordered materials. I. General theory. Physica 34, 325–332 (1967).
De Dycker, E. & Phariseau, P. On the LCAO-method for disordered materials. II. Application to some simple models. Physica 35, 405–416 (1967).
Kim, J. et al. Observation of tunable band gap and anisotropic Dirac semimetal state in black phosphorus. Science 349, 723–726 (2015).
Ryu, S. H. et al. Pseudogap in a crystalline insulator doped by disordered metals. Nature 596, 68–73 (2021).
Kiraly, B. et al. Anisotropic two-dimensional screening at the surface of black phosphorus. Phys. Rev. Lett. 123, 216403 (2019).
Baumberger, F., Auwärter, W., Greber, T. & Osterwalder, J. Electron coherence in a melting lead monolayer. Science 306, 2221–2224 (2004).
Rotenberg, E., Theis, W., Horn, K. & Gille, P. Quasicrystalline valence bands in decagonal AlNiCo. Nature 406, 602–605 (2000).
Corbae, P. et al. Observation of spin-momentum locked surface states in amorphous Bi2Se3. Nat. Mater. 22, 200–206 (2023).
Zhou, Y. et al. Bilayer Wigner crystals in a transition metal dichalcogenide heterostructure. Nature 595, 48–52 (2021).
Pudalov, V. M., D’lorio, M., Kravchenko, S. V. & Campbell, J. W. Zero-magnetic-field collective insulator phase in a dilute 2D electron system. Phys. Rev. Lett. 70, 1866–1869 (1993).
Hanein, Y. et al. Observation of the metal-insulator transition in two-dimensional n-type GaAs. Phys. Rev. B 58, R13338–R13340 (1993).
Solovyev, V. V. & Kukushkin, I. V. Renormalized Landau quasiparticle dispersion revealed by photoluminescence spectra from a two-dimensional Fermi liquid at the MgZnO/ZnO heterointerface. Phys. Rev. B 96, 115131 (2017).
Chui, S. T. & Tanatar, B. Impurity effect on the two-dimensional-electron fluid-solid transition in zero field. Phys. Rev. Lett. 74, 458–461 (1995).
Fogler, M. M., Koulakov, A. A. & Shklovskii, B. I. Ground state of a two-dimensional electron liquid in a weak magnetic field. Phys. Rev. B 54, 1853–1871 (1996).
Reichhardt, C. J. O., Reichhardt, C. & Bishop, A. R. Structural transitions, melting, and intermediate phases for stripe- and clump-forming systems. Phys. Rev. E 82, 041502 (2010).
Pu, S., Balram, A. C., Taylor, J., Fradkin, E. & Papić, Z. Microscopic model for fractional quantum Hall nematics. Phys. Rev. Lett. 132, 236503 (2024).
Chang, K. S., Sher, A., Petzinger, K. G. & Weisz, G. Density of states of liquid Cu. Phys. Rev. B 12, 5506–5513 (1975).
Anderson, P. W. & McMillan, W. L. in Multiple-Scattering Theory and Resonances in Transition Metals (ed. Marshall, W.) 50–86 (Academic, 1967).
Schwartz, L. & Ehrenreich, H. Single-site approximation in the electronic theory of liquid metals. Ann. Phys. 64, 100–148 (1971).
Morgan, G. J. Electron transport in liquid metals II. A model for the wave functions in liquid transition metals. J. Phys. C Solid State Phys. 2, 1454–1463 (1969).
Park, K. & Jain, J. K. Two-roton bound state in the fractional quantum Hall effect. Phys. Rev. Lett. 84, 5576–5579 (2000).
Jung, S. W. et al. Black phosphorus as a bipolar pseudospin semiconductor. Nat. Mater. 19, 277–281 (2020).
Golden, K. I., Kalman, G. J., Hartmann, P. & Donkó, Z. Dynamics of two-dimensional dipole systems. Phys. Rev. E 82, 036402 (2010).
Kutlu, E., Narin, P., Lisesivdin, S. B. & Ozbay, E. Electronic and optical properties of black phosphorus doped with Au, Sn and I atoms. Philos. Mag. 98, 155–164 (2018).
Fei, R. & Yang, L. Strain-engineering the anisotropic electrical conductance of few layer black phosphorus. Nano Lett. 14, 2884–2889 (2014).
Chui, S. T. & Tanatar, B. Phase diagram of the two-dimensional quantum electron freezing with external impurities. Phys. Rev. B 55, 9330–9932 (1997).
Tian, Z. et al. Isotropic charge screening of anisotropic black phosphorus revealed by potassium adatoms. Phys. Rev. B 100, 085440 (2019).
Shirley, E. L., Terminello, L. J., Santoni, A. & Himpsel, F. J. Brillouin-zone-selection effects in graphite photoelectron angular distributions. Phys. Rev. B 51, 13614–13622 (1995).
Moser, S. An experimentalist’s guide to the matrix element in angle resolved photoemission. J. Electron Spectros. Relat. Phenomena 214, 29–52 (2017).
Acknowledgements
This work was supported by National Research Foundation of Korea, which was funded by the Ministry of Science and ICT (Grant Nos. NRF-2021R1A3B1077156, NRF-RS-2024-00416976 and NRF-RS-2022-00143178) and the Yonsei Signature Research Cluster Program (Grant No. 2024-22-0163). This research also used resources of the Advanced Light Source (Contract No. DE-AC02-05CH11231), which is a US Department of Energy Office of Science user facility.
Author information
Authors and Affiliations
Contributions
S.P. performed the ARPES experiments with help from C.J., E.R. and A.B. and carried out the data analysis with help from M.H. K.S.K. conceived and directed the project. S.P. and K.S.K. wrote the manuscript with contributions from all other co-authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Raw ARPES data and curve-fitting.
a, Raw data of Fig. 1d, e shown in the form of EDCs over the k range from 0 to 1.005 Å–1 with the k interval of 0.067 Å–1. There are well-defined peaks even in the k region of weak intensity. For these well-defined peaks, it is straightforward by fitting each EDC with the Gaussian function (red lines overlaid) to reliably determine their peak positions as marked by red circles relative to E0 (dotted line). b-d, Peak position (b), width (c), and intensity (d) taken by curve-fitting in a and plotted as a function of ky. The error bars at maximum in b is smaller than the size of circled numbers. The light red line underlaid in b is the band dispersion calculated by our model30,31, which is in excellent agreement (quantitatively less than 4%). Even in the k range of weak intensity shaded in grey, the peak width in c is only 20% greater than that of strong intensity (this is related to the imaginary part of Δk in Extended Data Fig. 6a). On the other hand, the red curve overlaid in d shows the variation of intensity in conventional insulators across the zone boundary due to the well-known phase interference effect57,58. There is a small gap between peak intensity and the red curve, which means there remains relatively weak but finite intensity. e, Doping series of EDCs taken at the roton minimum or k2 and plotted relative to E0 (dotted line). Black lines overlaid are obtained by fitting each EDC with the Gaussian peak in colour, where their peak positions are marked by red ticks.
Extended Data Fig. 2 Direction dependence of electronic rotons.
a, Surface Brillouin zone of black phosphorus with high-symmetry points marked by open circles. Grey arrows show the three k directions indexed by kx, ks, and ky. b-d, ARPES data of black phosphorus doped by K at n = 3.8 x 1013 cm−2, taken along armchair (b), diagonal (c), and zigzag (d) directions corresponding to kx, ks, and ky, respectively. e-g, ARPES data obtained from those in b-d by normalizing the maximum intensity of EDCs at each k point. These normalized data reveal the clear signature of electronic rotons regardless of measurement directions.
Extended Data Fig. 3 Element dependence of electronic rotons.
a-d, ARPES data taken in ky for black phosphorus doped by Na (a), K (b), Rb (c), and Cs (d) at n = 3.8 ~ 5.3 × 1013 cm−2. Dotted lines show the magnitude of ΔPG, which is 106 meV for Na, 77 meV for K, 61 meV for Rb, and 48 meV for Cs as discussed in the previous report33. e-h, ARPES data obtained from those in a-d by normalizing the maximum intensity of EDCs at each k point. The normalized data show the clear signature of electronic rotons regardless of the kinds of alkali metals, which confirms that (i) it is not an artifact, and (ii) it is a generic property of alkali metals.
Extended Data Fig. 4 Comparison between ARPES data and simulations.
a-c, ARPES data (left panel) compared with simulations (right panel) for black phosphorus doped by K at n marked on top of each panel in units of 1013 cm−2 and rs. The band dispersion for simulations is obtained by fitting the peak position of ARPES data and the variation of spectral intensity as a function of k is obtained from the well-known phase interference effect57,58 (Methods). d-f, Corresponding ARPES data and spectral simulations after normalizing the intensity of peaks in each EDC. Our spectral simulations reproduce key aspects of not only raw data in a-c, but also normalized data in d-f.
Extended Data Fig. 5 Doping dependence of electronic rotons.
a-f, ARPES data taken for black phosphorus doped by K at n marked on top of each panel in units of 1013 cm−2 with rs. We found the pseudogap of 71−107 meV persistent in the range of n.
Extended Data Fig. 6 Complete electronic structure of liquid metals.
a,b Band dispersion (a) and probability density (b) of wavefunctions obtained by the theoretical model46,47,48,49 that was initially developed for liquid metals but can be generally applied to any non-crystalline system in the presence of the short-range order. There are two branches in terms of partial wave analysis46: One is the p-wave or d-wave states at resonance scattering predicted by Anderson and McMillan47 to show the back-bending band dispersion (due to the real part of Δk as shown by the black curve) and the pseudogap (due to the imaginary part of Δk as shown by the grey area), as shown in a. This is due to the formation of quasi-bound states (QBS), as shown by the black curve in b, within the scattering potential (dotted black line). The other is s-wave states49, for which resonance scattering is forbidden by the absence of a potential barrier as shown by the red dotted line in b. The presence of the unbound states represented by the red curve in b was predicted by Schwartz and Ehrenreich48 to be related to another aperiodic (damped oscillatory) branch in band dispersion that extends towards the zone boundary30,31 as shown by the red curve in a. The grey region surrounding the red curve shows the imaginary part of Δk that accounts for the small increase in the peak width of EDCs indicated by the red arrow in Extended Data Fig. 1c.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Park, S., Huh, M., Jozwiak, C. et al. Electronic rotons and Wigner crystallites in a two-dimensional dipole liquid. Nature 634, 813–817 (2024). https://doi.org/10.1038/s41586-024-08045-0
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41586-024-08045-0