Main

Quantum mechanics is based on the concept that the microscopic scale of our Universe contains inherent uncertainties in position and momentum that are fundamentally connected as σxσp ≥ ħ/2 (ref. 7). Using this theoretical description, the precise knowledge of the momentum width of a particle σp implies a corresponding uncertainty in the extent of its spatial wavefunction σx. When the object loses its ability to maintain coherence through interactions with the complex environmental bath, its position is localized. This localization of quantum objects heavily depends on the specific environment they are subjected to8. Recent efforts have primarily focused on constructing increasingly large coherent quantum systems9,10 and other highly delocalized objects to push measurement and other applications to—and beyond—the standard quantum limit11,12. Such experiments are at the frontiers of quantum science and engineering and aim, in part, to probe the interface between classical and quantum mechanics.

Here, by contrast, we present a new measurement concept: using highly localized unstable systems embedded in a complex solid-state material at a low temperature as a precision laboratory to probe the quantum properties of subatomic particles. We show that this concept is particularly powerful for investigating the properties of systems that are otherwise not directly accessible because of weak couplings in the Standard Model of particle physics, particularly the neutrino (ν).

Neutrinos are light, neutral leptons, and the only particles in the Standard Model that have an intrinsic chirality, in that they only interact through left-handed currents of the weak interaction through three flavour eigenstates, namely, νe, νμ and ντ. Neutrino oscillation experiments over the last 30 years13,14 have also indicated that these flavour eigenstates include at least two non-zero mass eigenstates. This observation of non-zero neutrino masses was awarded the Nobel Prize in Physics (2015), but it is still not known how the Standard Model should be extended to incorporate massive neutrinos15. The flavour oscillation effect for neutrinos arises from the fact that the mass eigenstates and weak-interaction eigenstates are not equal to each other, and because of their small interaction probabilities with the weak and gravitational forces, they are able to maintain coherence for long distances16. Thus, even for a neutrino created with a definite flavour—the electron neutrino (νe) in weak nuclear decay, for example—a coherent superposition of states exists in the neutrino wavepacket that affects the probability for observing a particular flavour as a function of time or distance from the source. As neutrinos propagate in space, their mass eigenstates separate owing to their different velocities, and eventually no longer overlap resulting in the decoherence of the group wavepacket17,18,19,20.

As neutrinos rarely interact with matter, they are notoriously difficult to detect. For example, a νe with 1 MeV kinetic energy has an interaction cross-section of roughly 10−42 cm2 (ref. 21). This fact also makes neutrinos attractive systems to study the fundamental properties of quantum mechanics and exotic new physics, because they are able to maintain coherence for long distances. Historically, observing these so-called ‘ghost particles’ from various sources requires large volume detectors with limited detection precision that run for several years22. These detectors rely on neutral-current and charged-current interactions with an atomic nucleus or electron in these large volumes21. The final-state particles are used to reconstruct the incoming neutrino energy and interaction point, along with the neutrino flavour for charged-current interactions. A deficit or excess flux of any flavour in the detector, compared with the flavour ratios at the source, is used to determine the oscillation probabilities as a function of energy and distance. Global data from neutrino oscillation experiments have been used to determine the mass splittings and mixing parameters for the three Standard Model neutrinos15. Moreover, data from the Daya Bay23,24, RENO25,26 and KamLAND27 reactor neutrino experiments currently provide loose indirect constraints on the spatial extent of \({\overline{\nu }}_{{\rm{e}}}\) wavepackets from β− decay sources5,6; however, νe wavepackets from electron-capture (EC) sources have never been studied.

To extract physics from the reactor oscillation experiments above, interpretation in the lepton mixing framework of the Standard Model is required15. Neutrino mixing parameters, matter effects and combining detector systematic uncertainties make extracting limits on σν,x a complex and difficult task. The current limits on wavepackets from reactor \({\overline{\nu }}_{{\rm{e}}}\) using this approach are 2.1 × 10−13 m ≤ σν,x ≤ 2 m (refs. 5,6). If the spatial widths of the \({\overline{\nu }}_{{\rm{e}}}\) and νe wavepackets are indeed near the low end of these limits, it has a considerable impact on the neutrino physics landscape, including alleviating tension in models for sterile neutrinos with electronvolt-scale masses through model-dependent fits to the available data28,29 and impacting the physics goals of JUNO30.

Given the current pervading anomalies in the neutrino physics landscape31, there is a need for new techniques that can provide model-independent access to the neutrino. Clever new experimental concepts have been presented to address this need using efficient, small-scale setups32,33,34 that are less model dependent and not limited by low neutrino interaction cross-sections. These experiments aim to precisely measure the low-energy recoiling atoms in nuclear EC decay35 to access information of the neutrino directly through its entanglement in the final state of radioactive decay. Of these new concepts, the beryllium EC in superconducting tunnel junctions (BeEST) experiment32 is currently the only one to practically use the concept of direct EC daughter recoil detection for neutrino physics36 and astrophysics37. Here we report, to our knowledge, the first direct limit on the spatial width of a neutrino wavepacket from the energy width of the recoiling nucleus in EC decay, σN,E, through their mutual entanglement.

Nuclear EC decay is a radioactive decay mode that results from the capture of an orbital electron by a proton in the nuclear volume35. At the fundamental level, this weak-interaction process transmutes an up quark to a down quark through the exchange of a W boson in a constituent nucleon and conserves the lepton number through the emission of νe. In the experimental context of the work presented here, the observable final state only contains two products: the recoiling heavy daughter system and νe. This simple two-body system that we observe is entangled at its creation, and thus, a precision measurement of the daughter recoil provides direct access to information on the neutrino.

The magnitude of σν,x is expected to depend on environmental factors, the type of decay and the scale of localizing interactions. Predictions based on localization through atomic interactions lead to an estimate of σν,x ≈ 200 nm for \({\overline{\nu }}_{{\rm{e}}}\) from reactor β− decay sources and σν,x ≈ 1–10 μm for νe from a 51Cr EC source1,3. Other theoretical approaches that assume localization through degrees of freedom in the nucleus for β− decay \({\overline{\nu }}_{{\rm{e}}}\) and degrees of freedom in the atom for EC νe lead to σν,x ≈ 10–400 pm for reactor β− decay sources and σν,x ≈ 3 nm for a beryllium-7 (7Be) EC source2,4. As these predictions vary by several orders of magnitude, a precise-enough wavepacket measurement from any nuclear-decay-based ν source could potentially distinguish between these competing theories on the scale of quantum localization in weak nuclear decays.

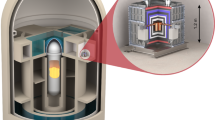
With seven nucleons and four electrons, the neutron-deficient 7Be nucleus is the simplest pure EC decaying system in the nuclear landscape. To measure the 7Be EC decay spectrum to high precision, we directly embedded the 7Be into the top tantalum film of a single superconducting tunnel junction (STJ) that was used as a high-energy-resolution sensor38. The STJ pixel used in this analysis was part of a 36-pixel array in which each sensor had a surface area of 208 × 208 μm2 and consisted of the following five layers (from top to bottom): Ta (165 nm)—Al (50 nm)—Al2O3 (1 nm)—Al (50 nm)—Ta (265 nm) (Fig. 1). This device was fabricated by photolithography at STAR Cryoelectronics39. STJs exploit the small energy gap in superconducting Ta (ΔTa ≈ 0.7 meV) to provide an intrinsic device energy resolution of 1–2 eV in the energy region of interest (approximately 100 eV).

Fig. 1: 7Be EC in an STJ.
figure 1

Schematic of the STJ sensor showing the five layers described in the text. The 7Be radioactive source is sparsely implanted into the Ta lattice of the absorber layer. The zoomed-in image (top right) shows the final state after EC decay including 7Li recoil and νe.

Full size image

Radioactive 7Be+ ions were directly implanted into the STJ pixel through apertures in a Si collimator that was situated approximately 100 μm above the chip. The 7Be+-ion beam was produced and delivered to the implantation chamber endstation at the TRIUMF-ISAC facility40 at an energy of 30 keV. The isotopically pure (almost 90%) 7Be+ beam was produced using the isotope separation on-line technique41 using spallation reactions from a 10 μA, 480 MeV proton beam incident on a stack of thin uranium carbide targets. Once released from the target through diffusion, the created beryllium atoms were selectively ionized using the ion guide laser ion source42 operated in suppression mode43. The resulting beam of 7Be+ ions was implanted at a rate of 6.1 × 106 s−1 for a period of 25 h to generate an initial per-pixel activity in the STJs of roughly 50 Bq. After implantation, the chip was cleaned and processed at TRIUMF to remove loose and surface-deposited activity and subsequently shipped to Lawrence Livermore National Laboratory (LLNL).

The final-state energy spectrum from the decay of 7Be was measured at LLNL with the STJ detector at a temperature of approximately 0.1 K in a two-stage adiabatic demagnetization refrigerator with liquid-nitrogen and liquid-helium precooling. Signal traces were read out continuously at a rate of 1.25 MSa s–1 at a 16-bit resolution using a PXIe-6356 analogue-to-digital converter. For the real-time in situ monitoring of the response and energy calibration, the STJs were simultaneously exposed to 3.49865(15) eV photons from a pulsed, 355 nm frequency-tripled Nd:YVO4 laser triggered at a rate of 100 Hz that was fed into the cold stage of the adiabatic demagnetization refrigerator through a fibre to illuminate the pixels. The laser intensity was adjusted such that multiphoton absorption provided a comb of peaks in the energy range from 20 eV to 120 eV. The energy resolution of the laser peaks was 1.85(1) eV at 108.5 eV with residuals of approximately 0.02 eV in the region of interest44,45. Selected data (Fig. 2) were acquired for approximately 20 h on 6 November 2022, which are a small subset of the full BeEST Phase-III dataset.

Fig. 2: The STJ array of the BeEST experiment and precision energy measurement.
figure 2

The measured 7Li recoil spectrum with the four peaks described in the text for 20 h of data from the single STJ pixel shown in the inset. The L-ES peak is barely visible because of its weak population probability. The measured uncertainty of the K-GS peak is shown, and is conservatively extracted as the upper limit on the inherent energy width of the recoil, σN,E ≤ 2.9 eV, through the procedure described in the text. The comb of the peaks from the calibration laser spectrum (violet) is also shown for comparison. The small bump in the spectrum at 4 eV results from a non-prompt, decay-induced process, the source of which is still under investigation. Scale bar, 1 mm.

Full size image

7Be decays to lithium-7 (7Li) and a νe with a half-life of T1/2 = 53.22(6) days46 and a total decay energy of QEC = 861.963(23) keV (ref. 47). In the EC process, the electron can be captured either from the 1s shell (K capture) or the 2s shell (L capture) of Be, with a measured L/K ratio of 0.070(7) (ref. 37). For K capture, the binding energy of the 1s hole is subsequently liberated by the emission of an Auger electron48. A small branch of 10.44(4)% results in the population of a short-lived excited nuclear state in 7Li (T1/2 = 72.8(20) fs) that de-excites by the emission of a 477.603(2) keV γ-ray46. As the nuclear decay and subsequent atomic relaxation occur on short timescales, our measurement method results in a low-energy spectrum with four peaks: two for K capture and two for L capture into the ground state (GS) and excited state (ES) of 7Li, all of which are well resolved. The two recoil peaks from the ES decay of 7Li are Doppler broadened from γ decay in flight37,38.

The final 7Be decay spectrum (Fig. 2) includes events from a single pixel that were not in coincidence with the laser logic pulse or simultaneous signals in other pixels. The latter of these two criteria was imposed to remove the large, low-energy background from 478 keV γ-ray Compton scattering interactions in the 0.5 mm Si substrate below the STJ array, which generated signals in many pixels simultaneously. The resulting EC recoil spectrum is dominated by the four expected peaks arising from the two atomic and two nuclear processes described above. A sophisticated analysis of the spectrum, which includes higher-order processes such as atomic shake-up and shake-off effects, is ongoing for the beyond-Standard Model physics search program of the BeEST experiment, but is not required here.

Only the K-GS peak is used in this analysis because it provides the highest statistical significance for a measurement of the recoil energy width with the smallest uncertainty and does not have Doppler broadening as the ES peaks do. The width of the K-GS recoil peak (Fig. 2) is broadened beyond the intrinsic resolution of the sensors based on the resolution of the laser peaks. Some of this width is because of structural and chemical variations of the Li 1s binding energy at different sites in the Ta lattice, which contribute \({\mathcal{O}}\)(1 eV) to the broadening49. However, owing to their complexity and the fact that these effects are not yet quantified in detail for the BeEST energy spectrum, we conservatively attributed all of the measured broadening in the K-GS peak to quantum uncertainty. This also ignores the negligible broadening caused by decays at the edges of the pixel50. A future analysis that accounts for known causes of broadening will improve the limits presented here.

The K-GS peak was fit in the region from 101 eV to 115 eV (Fig. 2) with a single Voigt function to extract the energy uncertainty width σN,E ≤ 2.9 eV at the 95% confidence level (CL) using the profile likelihood method51,52,53. We then converted the full energy width to a momentum width of the 7Li recoil. The uncertainty was propagated using \({\sigma }_{p}=\sqrt{m/2E}\,{\sigma }_{E}\), where m is the atomic mass of 7Li and E is energy of the K-GS peak centroid, resulting in σLi,p ≤ 16 keV c–1. Contributions due to the uncertainty in measurements of m are negligible54. Finally, using the Heisenberg uncertainty relation, we extracted a lower limit on the spatial width on the nuclear recoil of σN,x ≥ 6.2 pm. These results are based on our measurement of the K-GS peak energy width under the experimental conditions reported here and have no underlying assumptions about the scale of localization. Differences in the expected broadening owing to more realistic non-Gaussian wavepackets are negligible compared with other causes of variations in the broadening mentioned previously2.

To extract a limit on the neutrino spatial width σν,x, two approaches were used: one based on the conservation of energy1 and the other based on the conservation of momentum2. In the first method, the neutrino energy width is equivalent to that of the entangled recoil nucleus, which, in our case, is the upper limit on the measured energy width σν,E = σN,E ≤ 2.9 eV. This limit was then converted into a momentum uncertainty using the relativistic energy–momentum relation pν = Eν/c and σp = σE/c. The spatial uncertainty was extracted as σν,x ≥ 34 nm at the 95% CL using the uncertainty principle. As our conservative method includes effects from sources of inhomogeneous broadening mentioned previously, the actual homogeneous broadening related to quantum uncertainty is expected to be markedly smaller than this limit. We also note that this method is equivalent to the approach prescribed in ref. 17 in which the uncertainty in energy comes from the inverse of the time for which wavepackets overlap at production, which depends on the velocities of the nuclei in the source. Our measured upper limit on the energy uncertainty is approximately 3–10 times larger than predictions from models based on atomic-scale localization and uncertainty in the time between atomic interactions in the reactor and 51Cr sources1,3. Extending these theoretical models to make predictions for neutrinos emitted from nuclear decays in a sub-kelvin crystal lattice, as in the BeEST experiment, is beyond the scope of the present work.

For the second approach2, the momentum widths of the recoiling nucleus and neutrino are equivalent, that is, σν,p = σLi,p ≤ 16 keV c–1, and the uncertainty principle again gives the spatial width. Under this approach, we determine a lower limit on the spatial width of the neutrino of σν,x = σN,x ≥ 6.2 pm at the 95% CL (Fig. 3a). As the two methods described above yield markedly different results for the widths of the neutrino wavepackets (details of which are discussed extensively in the literature1,2,3,4,17), we do not claim the validity of one over the other here. We instead use the more conservative of the two to set our reported lower limits. The result is equivalent to combining the momentum and energy uncertainties as proposed in refs. 3,19,20.

Fig. 3: Experimental limits and theoretical predictions for radioactive-decay-based neutrino sources.
figure 3

a,b, Comparison between experimental limits (horizontal bars) and theoretical estimates (vertical bars) for the spatial extent of a neutrino wavepacket created in EC sources (a) and reactor β− sources (b). This plot encapsulates the current status of the spatial uncertainties of the neutrino wavepacket in both experiment and theory from the literature. For EC sources in a, the theoretical predictions are based on different scales of localization for νe. The blue band is based on the conservation of momentum and subatomic localization determined by the momentum uncertainty of the 7Li 1s electron orbital4. The red and orange bands are from two different predictions for atomic localization in a hot 51Cr source1,3. For the reactor sources in b, the experimental limits are indirectly inferred from various oscillation experiments5,6. The blue band from 10 pm to 400 pm is the theoretical estimate based on nucleon-scale/nucleus-scale localization estimates2. The orange and red bands are estimates based on localization by atomic interactions in the reactor local environment1,3. The bands on the far left spanning both plots correspond to the scenario in which the widths of the neutrino wavepackets are preferred in electronvolt-scale νs model fits to data28,29, and in the case of reactor sources, would also be the region that wavepacket separation would be visible in JUNO6,30.

Full size image

Establishing an experimental distinction between localization models, particularly for a purely weak-interaction-mediated transition under the emission of a neutrino, would be a quantitative test of scale decoupling in quantum field theory55, and may perhaps be the most important application of this technique in the future. For example, if the localizing interactions in weak nuclear decay are at the subatomic scale because of internal degrees of freedom in the nucleus2,4, the resulting wavepackets are expected to be several orders of magnitude smaller than if the decay product widths are set by atomic interactions1,3 (Fig. 3). A measurement precise enough to distinguish between these scenarios is expected to apply to all nuclear-decay-based ν sources and could serve as a fundamental test of quantum mechanics.

To perform a measurement that can distinguish the above models, our presented technique requires improvements and refinement in both analysis and detection methods. Potential improvements could come from accounting for known sources of broadening and minimizing lattice effects with more uniform superconducting films. We have shown that this technique can be applied to nuclear recoils of EC decay sources, but it may be possible to adapt it for the precision measurements of nuclear recoils of β± decay sources in STJs with the upcoming Superconducting Array for Low-Energy Radiation experiment at the Facility for Rare Isotope Beams. As nuclear β decay does not involve the capture of an orbital electron in the initial state, it could enable a direct comparison with β− sources and shed light on some of the fundamental questions on localization posed above (Fig. 3b).

The lower limit on the neutrino spatial width presented here does, however, provide potential insight into the suggestion that wavepacket separation may relieve tension in electronvolt-scale νs model fits with reactor experiments and the so-called ‘gallium anomaly’ in EC decay oscillation experiments. This improvement does, nevertheless, rely on the assumption that σν,x varies neglibly between reactor β decay \({\overline{\nu }}_{e}\) sources and 51Cr νe EC sources28. The same approach was also used to show that wavepacket separation could be one of the potential causes of the dampening-like effect that improves electronvolt-scale νs fits to global data29. The impact of wavepacket separation in these fits is marked near the current experimental lower limit from the reactor data of σν,x ≥ 210 fm but becomes indistinguishable from the plane-wave approximation at σν,x ≥ 2 pm (ref. 28). Our limit of σν,x ≥ 6.2 pm for an EC source, as shown in Fig. 3a along with the region favoured by νs models, disfavours wavepacket separation as the correct explanation for this anomaly, unless the reactor and 51Cr sources both produce ν much more localized than the BeEST 7Be source. The region preferred by νs models also corresponds to the sensitivity region of JUNO6,30. However, JUNO will detect \({\overline{\nu }}_{e}\) from nuclear reactors, and how this relates to an EC measurement depends on environmental factors and the scale of localization1,2,3,4.

In summary, we present a new experimental concept to measure the low-energy recoiling daughter system from highly localized EC decaying rare isotopes inside superconducting sensors. Using this method, we have been able to directly constrain the quantum localization scale of the final-state system in electroweak nuclear decay. Here we report a conservative upper limit of the energy width of the recoiling 7Li system from the EC decay of 7Be in a tantalum matrix at 0.1 K of σN,E ≤ 2.9 eV (95% CL). This corresponds to a limit on the spatial width of the 7Li nuclear recoil of σN,x ≥ 6.2 pm, which suggests that the localization of the final-state system occurs at a scale much larger than the nucleus in which the interaction occurs. From this measurement, we also set the same limit on the spatial width of the entangled neutrino, σν,x ≥ 6.2 pm, to our knowledge the first such limit on any EC νe source thus far and the first limit set by the direct measurements of the ν source. This limit disfavours wavepacket separation as the cause of dampening preferred by electronvolt-scale νs model fits to anomalous data. With planned future improvements to the analysis and detectors, this technique may be able to distinguish between competing models of localization in weak nuclear decays, and may provide a fundamental test of quantum mechanics.