Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Disorder-assisted real–momentum topological photonic crystal

Nature volume 639, pages 602–608 (2025)Cite this article

Subjects

Abstract

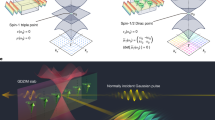
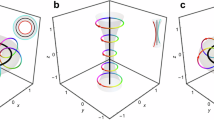
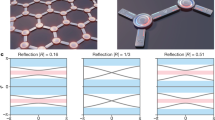
Topological defects and disorder counteract each other1,2,3,4,5. Intuitively, disorder is considered detrimental, requiring efforts to mitigate its effects in conventional topological photonics6,7,8,9. We propose a counter-intuitive approach that exploits a real–momentum topological photonic crystal that harnesses real-space disorder to generate a Pancharatnam–Berry phase10,11, without disrupting the momentum-space singularity originating from bound states in the continuum12. This methodology allows flat optical devices to encode spatial information or even extra topological charge in real space while preserving the topology of bound states in the continuum in momentum space with inherent alignment. Here, as a proof of concept, we demonstrate the simultaneous and independent generation of a real-space broadband vortex or a holographic image alongside resonant momentum-space vortex beams with a narrow bandwidth, which cannot be achieved with conventional methods. Such engineered disorder contributes to vast intrinsic freedoms without adding extra dimensions or compromising the optical flatness13,14. Our findings of real–momentum duality not only lay the foundation for disorder engineering in topological photonics but also open new avenues for optical wavefront shaping, encryption and communications.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Disorder-assisted real–momentum topological PhC.
Fig. 2: Robustness of momentum topology against disorder on notch geometries and rotation angles.
Fig. 3: Amplitude-modulated PB phase in real space for various rotation angles.
Fig. 4: Experiments on real–momentum vortex generation and topology duality.
Fig. 5: Experimental demonstration of real-space holography and momentum-space vortex with a single real–momentum topological PhC.

Similar content being viewed by others

Data availability

The data supporting the findings of this study are available in the article and the Supplementary Information.

References

  1. Jin, J. et al. Topologically enabled ultrahigh-Q guided resonances robust to out-of-plane scattering. Nature 574, 501–504 (2019).

    Article  ADS  CAS  PubMed  MATH  Google Scholar 

  2. Liu, C., Zhang, S., Maier, S. A. & Ren, H. Disorder-induced topological state transition in the optical skyrmion family. Phys. Rev. Lett. 129, 267401 (2022).

    Article  ADS  CAS  PubMed  Google Scholar 

  3. Lin, Z.-K. et al. Topological phenomena at defects in acoustic, photonic and solid-state lattices. Nat. Rev. Phys. 5, 483–495 (2023).

    Article  MATH  Google Scholar 

  4. Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2019).

    Article  ADS  MathSciNet  CAS  MATH  Google Scholar 

  5. Mermin, N. D. The topological theory of defects in ordered media. Rev. Mod. Phys. 51, 591–648 (1979).

    Article  ADS  MathSciNet  CAS  MATH  Google Scholar 

  6. Lu, L., Joannopoulos, J. D. & Soljačić, M. Topological photonics. Nat. Photon. 8, 821–829 (2014).

    Article  ADS  CAS  Google Scholar 

  7. Yu, S., Qiu, C.-W., Chong, Y., Torquato, S. & Park, N. Engineered disorder in photonics. Nat. Rev. Mater. 6, 226–243 (2021).

    Article  ADS  CAS  Google Scholar 

  8. Shapiro, J. & Tauber, C. Strongly disordered Floquet topological systems. Ann. Henri Poincaré 20, 1837–1875 (2019).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  9. Zhang, Z., Delplace, P. & Fleury, R. Superior robustness of anomalous non-reciprocal topological edge states. Nature 598, 293–297 (2021).

    Article  ADS  CAS  PubMed  PubMed Central  MATH  Google Scholar 

  10. Lin, D., Fan, P., Hasman, E. & Brongersma, M. L. Dielectric gradient metasurface optical elements. Science 345, 298–302 (2014).

    Article  ADS  CAS  PubMed  MATH  Google Scholar 

  11. Song, Q. et al. Ptychography retrieval of fully polarized holograms from geometric-phase metasurfaces. Nat. Commun. 11, 2651 (2020).

    Article  ADS  CAS  PubMed  PubMed Central  MATH  Google Scholar 

  12. Wang, B. et al. Generating optical vortex beams by momentum-space polarization vortices centred at bound states in the continuum. Nat. Photon. 14, 623–628 (2020).

    Article  ADS  CAS  MATH  Google Scholar 

  13. Dorrah, A. H. & Capasso, F. Tunable structured light with flat optics. Science 376, eabi6860 (2022).

    Article  CAS  PubMed  MATH  Google Scholar 

  14. Chen, W. T., Zhu, A. Y. & Capasso, F. Flat optics with dispersion-engineered metasurfaces. Nat. Rev. Mater. 5, 604–620 (2020).

    Article  ADS  MATH  Google Scholar 

  15. Khanikaev, A. B. & Alù, A. Topological photonics: robustness and beyond. Nat. Commun. 15, 931 (2024).

    Article  ADS  CAS  PubMed  PubMed Central  MATH  Google Scholar 

  16. He, L. et al. Floquet Chern insulators of light. Nat. Commun. 10, 4194 (2019).

    Article  ADS  PubMed  PubMed Central  MATH  Google Scholar 

  17. Biesenthal, T. et al. Fractal photonic topological insulators. Science 376, 1114–1119 (2022).

    Article  ADS  CAS  PubMed  MATH  Google Scholar 

  18. Pyrialakos, G. G. et al. Bimorphic Floquet topological insulators. Nat. Mater. 21, 634–639 (2022).

    Article  ADS  CAS  PubMed  MATH  Google Scholar 

  19. Dutt, A., Minkov, M., Williamson, I. A. D. & Fan, S. Higher-order topological insulators in synthetic dimensions. Light: Sci. Appl. 9, 131 (2020).

    Article  ADS  CAS  PubMed  Google Scholar 

  20. Kruk, S. et al. Nonlinear light generation in topological nanostructures. Nat. Nanotechnol. 14, 126–130 (2019).

    Article  ADS  CAS  PubMed  MATH  Google Scholar 

  21. Hwang, M.-S. et al. Vortex nanolaser based on a photonic disclination cavity. Nat. Photon. 18, 286–293 (2024).

    Article  ADS  CAS  MATH  Google Scholar 

  22. Wang, Y. et al. Hybrid topological photonic crystals. Nat. Commun. 14, 4457 (2023).

    Article  ADS  CAS  PubMed  PubMed Central  MATH  Google Scholar 

  23. Kim, M., Jacob, Z. & Rho, J. Recent advances in 2D, 3D and higher-order topological photonics. Light: Sci. Appl. 9, 130 (2020).

    Article  ADS  PubMed  MATH  Google Scholar 

  24. Song, Q., Odeh, M., Zúñiga-Pérez, J., Kanté, B. & Genevet, P. Plasmonic topological metasurface by encircling an exceptional point. Science 373, 1133–1137 (2021).

    Article  ADS  CAS  PubMed  Google Scholar 

  25. You, J. W. et al. Topological metasurface: from passive toward active and beyond. Photonics Res. 11, B65–B102 (2023).

    Article  MATH  Google Scholar 

  26. Joannopoulos, J. D., Johnson, S. G., Winn, J. N. & Meade, R. D. Photonic Crystals: Molding the Flow of Light (Princeton Univ. Press, 2008).

  27. Chen, Z. & Segev, M. Highlighting photonics: looking into the next decade. eLight 1, 2 (2021).

    Article  CAS  MATH  Google Scholar 

  28. Hsu, C. W., Zhen, B., Stone, A. D., Joannopoulos, J. D. & Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 1, 16048 (2016).

    Article  ADS  CAS  MATH  Google Scholar 

  29. Zhen, B., Hsu, C. W., Lu, L., Stone, A. D. & Soljačić, M. Topological nature of optical bound states in the continuum. Phys. Rev. Lett. 113, 257401 (2014).

    Article  ADS  PubMed  Google Scholar 

  30. Koshelev, K., Bogdanov, A. & Kivshar, Y. Meta-optics and bound states in the continuum. Sci. Bull. 64, 836–842 (2019).

    Article  Google Scholar 

  31. Wang, J. et al. Optical bound states in the continuum in periodic structures: mechanisms, effects, and applications. Photonics Insights 3, R01 (2024).

    Article  Google Scholar 

  32. Qin, H. et al. Arbitrarily polarized bound states in the continuum with twisted photonic crystal slabs. Light: Sci. Appl. 12, 66 (2023).

    Article  ADS  CAS  PubMed  MATH  Google Scholar 

  33. Kodigala, A. et al. Lasing action from photonic bound states in continuum. Nature 541, 196–199 (2017).

    Article  ADS  CAS  PubMed  Google Scholar 

  34. Huang, C. et al. Ultrafast control of vortex microlasers. Science 367, 1018–1021 (2020).

    Article  ADS  CAS  PubMed  MATH  Google Scholar 

  35. Zhai, Z. et al. Multimode vortex lasing from dye–TiO2 lattices via bound states in the continuum. ACS Photonics 10, 437–446 (2023).

    Article  CAS  MATH  Google Scholar 

  36. Chen, Y. et al. Compact spin-valley-locked perovskite emission. Nat. Mater. 22, 1065–1070 (2023).

    Article  ADS  CAS  PubMed  MATH  Google Scholar 

  37. Wang, Z., Chong, Y., Joannopoulos, J. D. & Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009).

    Article  ADS  CAS  PubMed  MATH  Google Scholar 

  38. Bahari, B. et al. Nonreciprocal lasing in topological cavities of arbitrary geometries. Science 358, 636–640 (2017).

    Article  ADS  CAS  PubMed  MATH  Google Scholar 

  39. Ye, W., Gao, Y. & Liu, J. Singular points of polarizations in the momentum space of photonic crystal slabs. Phys. Rev. Lett. 124, 153904 (2020).

    Article  ADS  CAS  PubMed  MATH  Google Scholar 

  40. Koshelev, K., Lepeshov, S., Liu, M., Bogdanov, A. & Kivshar, Y. Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum. Phys. Rev. Lett. 121, 193903 (2018).

    Article  ADS  PubMed  Google Scholar 

  41. Liu, W. et al. Circularly polarized states spawning from bound states in the continuum. Phys. Rev. Lett. 123, 116104 (2019).

    Article  ADS  CAS  PubMed  MATH  Google Scholar 

  42. Cohen, E. et al. Geometric phase from Aharonov–Bohm to Pancharatnam–Berry and beyond. Nat. Rev. Phys. 1, 437–449 (2019).

    Article  MATH  Google Scholar 

  43. Song, Q., Liu, X., Qiu, C.-W. & Genevet, P. Vectorial metasurface holography. Appl. Phys. Rev. 9, 011311 (2022).

    Article  ADS  CAS  Google Scholar 

  44. Yang, Z. et al. Asymmetric full-color vectorial meta-holograms empowered by pairs of exceptional points. Nano Lett. 24, 844–851 (2024).

    Article  ADS  CAS  PubMed  MATH  Google Scholar 

  45. Yu, Z. et al. A spatial-frequency patching metasurface enabling super-capacity perfect vector vortex beams. eLight 4, 21 (2024).

    Article  MATH  Google Scholar 

  46. Lv, W. et al. Robust generation of intrinsic C points with magneto-optical bound states in the continuum. Sci. Adv. 10, eads0157 (2024).

    Article  ADS  PubMed  PubMed Central  MATH  Google Scholar 

  47. Huang, S. H. et al. Microcavity-assisted multi-resonant metasurfaces enabling versatile wavefront engineering. Nat. Commun. 15, 9658 (2024).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  48. Yu, Z. et al. High-security learning-based optical encryption assisted by disordered metasurface. Nat. Commun. 15, 2607 (2024).

    Article  ADS  CAS  PubMed  PubMed Central  MATH  Google Scholar 

  49. Zhang, Z., Wang, J., Qin, H. & Fleury, R. Floquet topological physics in photonics. Preprint at https://doi.org/10.1364/opticaopen.27930081.v1 (2024).

  50. Gahagan, K. T. & Swartzlander, G. A. Optical vortex trapping of particles. Opt. Lett. 21, 827–829 (1996).

    Article  ADS  CAS  PubMed  MATH  Google Scholar 

Download references

Acknowledgements

Q.S. acknowledges funding support from the National Natural Science Foundation of China (grant nos. 12474388 and 12204264) and the Shenzhen Science and Technology Innovation Commission (grant no. JCYJ20230807111706014). This work is also funded by the Basic Research Program of Jiangsu (grant no. BK20243029). H.Q., Z.Z. and R.F. acknowledge funding support from the Swiss State Secretariat for Education, Research and Innovation (contract no. MB22.00028). C.-W.Q. acknowledges support from the Ministry of Education in Singapore (grant nos. A-8002152-00-00 and A-8002458-00-00) and a Competitive Research Program Award from the NRF, Prime Minister’s Office, Singapore (grant nos. NRF-CRP22-2019-0006 and NRF-CRP26-2021-0004). H.Q. and Z.S. thank H. Yang for help with instrumentation.

Author information

Author notes

  1. These authors contributed equally: Haoye Qin, Zengping Su, Zhe Zhang

Authors and Affiliations

  1. Institute of Materials Research (IMR), Tsinghua Shenzhen International Graduate School, Tsinghua University, Shenzhen, China

    Haoye Qin, Zengping Su, Wenjing Lv, Zijin Yang, Xinyue Gao, Bo Li & Qinghua Song

  2. Laboratory of Wave Engineering, École Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland

    Haoye Qin, Zhe Zhang & Romain Fleury

  3. School of Materials Science and Engineering, Tsinghua University, Beijing, China

    Zengping Su, Wenjing Lv, Zijin Yang & Ji Zhou

  4. Department of Electrical and Computer Engineering, National University of Singapore, Singapore, Singapore

    Weijin Chen, Heng Wei & Cheng-Wei Qiu

  5. Institute of Precision Optical Engineering, School of Physics Science and Engineering, Tongji University, Shanghai, China

    Yuzhi Shi

  6. Suzhou Laboratory, Suzhou, China

    Bo Li & Qinghua Song

Authors
  1. Haoye Qin
    View author publications

    Search author on:PubMed Google Scholar

  2. Zengping Su
    View author publications

    Search author on:PubMed Google Scholar

  3. Zhe Zhang
    View author publications

    Search author on:PubMed Google Scholar

  4. Wenjing Lv
    View author publications

    Search author on:PubMed Google Scholar

  5. Zijin Yang
    View author publications

    Search author on:PubMed Google Scholar

  6. Weijin Chen
    View author publications

    Search author on:PubMed Google Scholar

  7. Xinyue Gao
    View author publications

    Search author on:PubMed Google Scholar

  8. Heng Wei
    View author publications

    Search author on:PubMed Google Scholar

  9. Yuzhi Shi
    View author publications

    Search author on:PubMed Google Scholar

  10. Bo Li
    View author publications

    Search author on:PubMed Google Scholar

  11. Ji Zhou
    View author publications

    Search author on:PubMed Google Scholar

  12. Romain Fleury
    View author publications

    Search author on:PubMed Google Scholar

  13. Cheng-Wei Qiu
    View author publications

    Search author on:PubMed Google Scholar

  14. Qinghua Song
    View author publications

    Search author on:PubMed Google Scholar

Contributions

H.Q., R.F. and Q.S. conceived the project. H.Q. carried out the numerical simulations. H.Q. and Z.S. fabricated the samples and conducted the measurements. H.Q., Z.Z., Z.S. and W.L. analysed the results and performed the visualizations. Z.Y., W.C., X.G. and H.W. provided technical support. H.Q., Z.Z., W.L. and Q.S. wrote the manuscript. H.Q., Z.Y., W.C., R.F., C.-W.Q., Y.S., B.L., J.Z. and Q.S. revised the manuscript. R.F., C.-W.Q. and Q.S. supervised the entire project. All authors discussed the results and commented on the article.

Corresponding authors

Correspondence to Romain Fleury, Cheng-Wei Qiu or Qinghua Song.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature thanks Alex Krasnok, Gianluca Ruffato and Lei Shi for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

This file contains Supplementary Figs. 1–29 and Notes 1–8.

Supplementary Video 1

Wavelength-engineered real–momentum topology duality.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Qin, H., Su, Z., Zhang, Z. et al. Disorder-assisted real–momentum topological photonic crystal. Nature 639, 602–608 (2025). https://doi.org/10.1038/s41586-025-08632-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41586-025-08632-9

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing