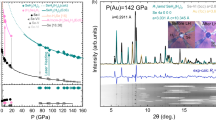
Abstract
The structural evolution of molecular hydrogen H2 under multi-megabar compression and its relation to atomic metallic hydrogen is a key unsolved problem in condensed-matter physics. Although dozens of crystal structures have been proposed by theory1,2,3,4, only one, the simple hexagonal-close-packed (hcp) structure of only spherical disordered H2, has been previously confirmed in experiments5. Through advancing nano-focused synchrotron X-ray probes, here we report the observation of the transition from hcp H2 to a post-hcp structure with a six-fold larger supercell at pressures above 212 GPa, indicating the change of spherical H2 to various ordered configurations. Theoretical calculations based on our XRD results found a time-averaged structure model in the space group \(P\bar{6}2c\) with alternating layers of spherically disordered H2 and new graphene-like layers consisting of H2 trimers (H6) formed by the association of three H2 molecules. This supercell has not been reported by any previous theoretical study for the post-hcp phase, but is close to a number of theoretical models with mixed-layer structures. The evidence of a structural transition beyond hcp establishes the trend of H2 molecular association towards polymerization at extreme pressures, giving clues about the nature of the molecular-to-atomic transition of metallic hydrogen. Considering the spectroscopic behaviours that show strong vibrational and bending peaks of H2 up to 400 GPa, it would be prudent to speculate the continuation of hydrogen molecular polymerization up to its metallization.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$32.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon request. Raw SCXRD data are available at Zenodo (https://zenodo.org/uploads/14032134)53. Source data are provided with this paper.
References
Pickard, C. J. & Needs, R. J. Structure of phase III of solid hydrogen. Nat. Phys. 3, 473–476 (2007).
McMahon, J. M., Morales, M. A., Pierleoni, C. & Ceperley, D. M. The properties of hydrogen and helium under extreme conditions. Rev. Mod. Phys. 84, 1607–1653 (2012).
Monserrat, B. et al. Structure and metallicity of phase V of hydrogen. Phys. Rev. Lett. 120, 255701 (2018).
Monacelli, L., Casula, M., Nakano, K., Sorella, S. & Mauri, F. Quantum phase diagram of high-pressure hydrogen. Nat. Phys. 19, 845–850 (2023).
Hazen, R. M., Mao, H. K., Finger, L. W. & Hemley, R. J. Single-crystal x-ray diffraction of n-H2 at high pressure. Phys. Rev. B 36, 3944–3947 (1987).
Ginzburg, V. L. Nobel Lecture: on superconductivity and superfluidity (what I have and have not managed to do) as well as on the “physical minimum” at the beginning of the XXI century. Rev. Mod. Phys. 76, 981–998 (2004).
Ashcroft, N. W. Metallic hydrogen: a high-temperature superconductor?. Phys. Rev. Lett. 21, 1748–1749 (1968).
Wigner, E. & Huntington, H. B. On the possibility of a metallic modification of hydrogen. J. Chem. Phys. 3, 764 (1935).
Mao, H. K. et al. Synchrotron X-ray diffraction measurements of single-crystal hydrogen to 26.5 gigapascals. Science 239, 1131–1134 (1988).
Loubeyre, P. et al. X-ray diffraction and equation of state of hydrogen at megabar pressures. Nature 383, 702–704 (1996).
Eremets, M. I., Drozdov, A. P., Kong, P. P. & Wang, H. Semimetallic molecular hydrogen at pressure above 350 GPa. Nat. Phys. 15, 1246–1249 (2019).
Loubeyre, P., Occelli, F. & Dumas, P. Synchrotron infrared spectroscopic evidence of the probable transition to metal hydrogen. Nature 577, 631–635 (2020).
Goncharenko, I. & Loubeyre, P. Neutron and X-ray diffraction study of the broken symmetry phase transition in solid deuterium. Nature 435, 1206–1209 (2005).
Akahama, Y. et al. Evidence from x-ray diffraction of orientational ordering in phase III of solid hydrogen at pressures up to 183 GPa. Phys. Rev. B 82, 060101 (2010).
Ji, C. et al. Ultrahigh-pressure isostructural electronic transitions in hydrogen. Nature 573, 558–562 (2019).
Mao, H.-k. & Hemley, R. J. Ultrahigh-pressure transitions in solid hydrogen. Rev. Mod. Phys. 66, 671–692 (1994).
Eremets, M. I. & Troyan, I. A. Conductive dense hydrogen. Nat. Mater. 10, 927–931 (2011).
Howie, R. T., Guillaume, C. L., Scheler, T., Goncharov, A. F. & Gregoryanz, E. Mixed molecular and atomic phase of dense hydrogen. Phys. Rev. Lett. 108, 125501 (2012).
Howie, R. T., Scheler, T., Guillaume, C. L. & Gregoryanz, E. Proton tunneling in phase IV of hydrogen and deuterium. Phys. Rev. B 86, 214104 (2012).
Dalladay-Simpson, P., Howie, R. T. & Gregoryanz, E. Evidence for a new phase of dense hydrogen above 325 gigapascals. Nature 529, 63–67 (2016).
Mazin, I. I., Hemley, R. J., Goncharov, A. F., Hanfland, M. & Mao, H.-k Quantum and classical orientational ordering in solid hydrogen. Phys. Rev. Lett. 78, 1066–1069 (1997).
Nagara, H. & Nakamura, T. Stable phases of solid hydrogen at megabar pressures and at zero temperature. Phys. Rev. Lett. 68, 2468–2471 (1992).
Natoli, V., Martin, R. M. & Ceperley, D. Crystal structure of molecular hydrogen at high pressure. Phys. Rev. Lett. 74, 1601–1604 (1995).
Johnson, K. A. & Ashcroft, N. W. Structure and bandgap closure in dense hydrogen. Nature 403, 632–635 (2000).
Kitamura, H., Tsuneyuki, S., Ogitsu, T. & Miyake, T. Quantum distribution of protons in solid molecular hydrogen at megabar pressures. Nature 404, 259–262 (2000).
Liu, H., Zhu, L., Cui, W. & Ma, Y. Room-temperature structures of solid hydrogen at high pressures. J. Chem. Phys. 137, 074501 (2012).
Pickard, C. J., Martinez-Canales, M. & Needs, R. J. Density functional theory study of phase IV of solid hydrogen. Phys. Rev. B 85, 214114 (2012).
Niu, H. et al. Stable solid molecular hydrogen above 900 K from a machine-learned potential trained with diffusion quantum Monte Carlo. Phys. Rev. Lett. 130, 076102 (2023).
Babaev, E., Sudbø, A. & Ashcroft, N. W. A superconductor to superfluid phase transition in liquid metallic hydrogen. Nature 431, 666–668 (2004).
Bonev, S. A., Schwegler, E., Ogitsu, T. & Galli, G. A quantum fluid of metallic hydrogen suggested by first-principles calculations. Nature 431, 669 (2004).
Ji, C. et al. Crystallography of low Z material at ultrahigh pressure: case study on solid hydrogen. Matter Radiat. Extremes 5, 038401 (2020).
Bjorling, A. et al. Ptychographic characterization of a coherent nanofocused X-ray beam. Opt. Express 28, 5069–5076 (2020).
Carbone, D. et al. Design and performance of a dedicated coherent X-ray scanning diffraction instrument at beamline NanoMAX of MAX IV. J. Synchrotron Radiat. 29, 876–887 (2022).
Johansson, U. et al. NanoMAX: the hard X-ray nanoprobe beamline at the MAX IV Laboratory. J. Synchrotron Radiat. 28, 1935–1947 (2021).
Glazyrin, K. et al. Sub-micrometer focusing setup for high-pressure crystallography at the Extreme Conditions beamline at PETRA III. J. Synchrotron Radiat. 29, 654–663 (2022).
Goncharov, A. F., Chuvashova, I., Ji, C. & Mao, H. K. Intermolecular coupling and fluxional behavior of hydrogen in phase IV. Proc. Natl Acad. Sci. USA 116, 25512–25515 (2019).
Eremets, M. I., Troyan, I. A., Lerch, P. & Drozdov, A. Infrared study of hydrogen up to 310 GPa at room temperature. High Pressure Res. 33, 377–380 (2013).
Loubeyre, P., Occelli, F. & Dumas, P. Hydrogen phase IV revisited via synchrotron infrared measurements in H2 and D2 up to 290 GPa at 296 K. Phys. Rev. B 87, 134101 (2013).
Zha, C.-S., Liu, Z., Ahart, M., Boehler, R. & Hemley, R. J. High-pressure measurements of hydrogen phase IV using synchrotron infrared spectroscopy. Phys. Rev. Lett. 110, 217402 (2013).
Liu, H. & Ma, Y. Proton or deuteron transfer in phase IV of solid hydrogen and deuterium. Phys. Rev. Lett. 110, 025903 (2013).
Magdău, I. B. & Ackland, G. J. Identification of high-pressure phases III and IV in hydrogen: Simulating Raman spectra using molecular dynamics. Phys. Rev. B 87, 174110 (2013).
Geneste, G., Torrent, M., Bottin, F. & Loubeyre, P. Strong isotope effect in phase II of dense solid hydrogen and deuterium. Phys. Rev. Lett. 109, 155303 (2012).
Ackland, G. J. & Loveday, J. S. Structures of solid hydrogen at 300 K. Phys. Rev. B 101 094104 (2020).
Monserrat, B., Needs, R. J., Gregoryanz, E. & Pickard, C. J. Hexagonal structure of phase III of solid hydrogen. Phys. Rev. B 94, 134101 (2016).
Holland, T. J. B. & Redfern, S. A. T. Unit cell refinement from powder diffraction data: the use of regression diagnostics. Mineral. Mag. 61, 65–77 (1997).
Ji, C., Li, B., Yang, W. & Mao, H.-k. Crystallographic studies of ultra-dense solid hydrogen. Chin. J. High Press. Phys. 34, 020101 (2020).
Prescher, C. & Prakapenka, V. B. DIOPTAS: a program for reduction of two-dimensional X-ray diffraction data and data exploration. High Press. Res. 35, 223–230 (2015).
Wojdyr, M. Fityk: a general-purpose peak fitting program. J. Appl. Crystallogr. 43, 1126–1128 (2010).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Perdew, J. P. et al. Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 46, 6671–6687 (1992).
Blochl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Shiga, M., Tachikawa, M. & Miura, S. Ab initio molecular orbital calculation considering the quantum mechanical effect of nuclei by path integral molecular dynamics. Chem. Phys. Lett. 332, 396–402 (2000).
Ji, C. Raw SCXRD data of ‘Ultrahigh Pressure Crystallographic Passage Toward Metallic Hydrogen’ v.1.0. Zenodo. https://doi.org/10.21203/rs.3.rs-5080559/v1 (2025).
Acknowledgements
We thank H. Shu for assistance with gas loading systems. We acknowledge financial supports from the National Science Foundation of China (NSFC) 12074014, the National Key Research and Development Program of China 2023YFA1608902 and 2022YFA1402301, the NSFC U2230401, 52288102, 52090024 and T2495233, the Shanghai Science and Technology Committee, China (no. 22JC1410300), the Shanghai Key Laboratory of Material Frontiers Research in Extreme Environments, China (no. 22dz2260800) and the Fundamental Research Funds for the Central Universities. This is also a contribution to the project of Theory of Hydrocarbon Enrichment under Multi-Spheric Interactions of the Earth (THEMSIE04010102). Portions of this work were performed at P02.2, Petra III, Deutsches Elektronen Synchrotron (DESY) in Germany, NanoMAX, MAX IV in Sweden, 34-ID-E, Advanced Photon Source (APS), Argonne National Laboratory (ANL) in the United States, as well as BL15U1, Shanghai Synchrotron Radiation Facility (SSRF) in China. We acknowledge the MAX IV Laboratory for time on Beamline NanoMAX under proposals 20190637, 20220481 and 20230465. Research conducted at MAX IV, a Swedish national user facility, is supported by the Swedish Research Council under contract no. 2018-07152, the Swedish Governmental Agency for Innovation Systems, under contract no. 2018-04969 and Formas under contract no. 2019-02496. This research used resources of the Advanced Photon Source, a US Department of Energy, Office of Science User Facility, operated by Argonne National Laboratory under contract no. DE-AC02-06CH11357.
Author information
Authors and Affiliations
Contributions
H.-K.M. conceived and supervised the project; C.J., B.L., Y.Z., K.G., A.B., L.A.B.M. and Y.G. performed synchrotron SCXRD measurements; K.G., A.B., M.K., S.K. and W.L. developed and set up the synchrotron nano-probe beamlines; C.J. and J.W. improved the sample preparation techniques for nano-probe SCXRD measurements with C.J. preparing ultrahigh-pressure hydrogen samples; C.J., H.-K.M. and Y.D. performed data analysis; J.L., Y.L., H.L. and Y.M. performed theoretical calculations. H.-K.M., C.J. and W.L.M. wrote the paper in consultation with K.G., L.A.B.M., J.L., H.L. and W.Y.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Guoyin Shen and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Post-hcp data points in phase diagram.
(a) Phase diagram of hydrogen. Lines represent phase boundary, stars represent pressure points at which SCXRD data indicate a post-hcp structure. All data were collected at room temperature. Similarity in colours of phases IV, IV’, and V represents their similarity in crystal structure as indicated by spectroscopic data. The drawing of this phase diagram takes references of previous studies11,18,20. (b) Enlarged view of the phase diagram included in the red dash box in (a).
Extended Data Fig. 2 Qualities of rotation center alignment with and without Au position marker.
(a) Micro-image of H2 sealed in MgO-epoxy insert gasket without Au position marker. (b) Rotation center alignment by scanning MgO (2 0 0) peak at three different angles. Position with no MgO peak is where H2 is located. Dash lines mark the center positions of H2 at different angles. (c) and (d) show micro-images of H2 sealed in MgO-epoxy insert gasket with Au position marker with transmitted light and reflected light illumination, respectively. A piece of 2 to 3 μm Au was loaded nearby H2 sample. (e) Rotation center alignment by scanning Au (1 1 1) Bragg peak at three different angles. Dash lines mark the center positions of Au at different angles. With Au position marker, the precision of rotation center alignment is substantially improved.
Extended Data Fig. 3 Rocking curves of Bragg peaks measured in ten crystal grains.
(a) and (b) belong to the data measured at 221 GPa and 245 GPa (corresponding to Fig. 1g and f, respectively). (c) to (j) belong to grains #8, #1, #2, #3, #4, #6, #7, and #9 measured at 233 GPa, 212 GPa, 212 GPa, 213 GPa, 218 GPa, 223 GPa, 232 GPa, and 243 GPa, respectively. Such sharp rocking curves are typical for hydrogen at two megabar pressures measured using nano-probe. Miller indexes are in the \(\sqrt{3}\) × a 2 × c supercell. In each crystal grain, intensity is normalized against the strongest Bragg peak, of which the value is set to 100.
Extended Data Fig. 4 Raw XRD images of the other seven crystal grains measured at 212 GPa (a), 212 GPa (b), 213 GPa (c), 218 GPa (d), 223 GPa (e), 232 GPa (f), 243 GPa (g), and 233 GPa (h), respectively.
Those XRD images were also merged from selected step scan images. Small boxes in XRD images mark the peak positions, with magnified views of the peaks in the red rectangles. Numbers are Miller indices in the \(\sqrt{3}\) × a 2 × c hexagonal supercell. Red indices mark peaks uniquely belonging to the \(\sqrt{3}\) × a 2 × c hexagonal supercell, while white indices mark peaks which are also allowed by the hcp symmetry.
Extended Data Fig. 5 Atomic trajectories and free energy of \({\boldsymbol{P}}\bar{{\bf{6}}}{\bf{2}}{\boldsymbol{c}}\).
(a) Atomic trajectory of H from MD simulations with a total time of 2 ps. (b) Atomic trajectory of H from PIMD simulations with a total time of 2 ps. Red and purple dots represent atomic trajectory in G1 and G2 layers, respectively. Blue dots represent atomic trajectory in B layers. (c) Free energies of the P\(\bar{6}2\)c, Cmca-4 and I41/amd structures relative to C2/c−24 at 250 GPa using the phonon DOS derived from MD simulations. The shaded region indicates the error range through comparison with results obtained from static phonon calculations.
Extended Data Fig. 6 Simulated XRD pattern based on the \({\boldsymbol{P}}\bar{{\bf{6}}}{\bf{2}}{\boldsymbol{c}}\) model calculated at 250 GPa.
Red and blue bars represent calculated intensities. Red bars mark peaks uniquely belonging to the \(P\bar{6}2c\) model. Blue bars mark peaks also allowed by the parent hcp unit cell. Spheres mark at what pressures the corresponding Bragg peaks were observed. Spheres are only to demonstrate the statistics of observed peaks, and do not reflect the true d-spacing of those peaks at their observed pressures.
Extended Data Fig. 7 Comparison of Bragg peaks of different structural models in a d-spacing range of 1.15 Å to 2.5 Å to that of \({\boldsymbol{P}}\bar{{\bf{6}}}{\bf{2}}{\boldsymbol{c}}\).
Red bars represent intensity of Bragg peaks. Blue dash lines mark unique supercell peaks, red dash lines mark peaks which are also allowed by hcp-like unit cell. Intensities of Bragg peaks were calculated by using software PCW. Peak intensity generated by PCW of one peak was divided by the multiplicity of that peak. Unit cell parameters of all models were derived based on hcp-like unit cell parameters measured at 245 GPa (a0 = 1.6969 Å and c0 = 2.6124 Å), assuming those lattices being perfect supercell of the hcp lattice (in reality, most theoretical models are distorted from the perfect supercell geometry). Specifically, the geometry relationships are listed as the following: Pca21 (phase II), \(a=\sqrt{3}\cdot \)a0 b = a0 c = c0 α = 90.0° β = 90.0° γ = 90.0°; P63/m (phase II), \(a=2\cdot \)a0 b = 2∙a0 c = c0 α = 90.0° β = 90.0° γ = 120.0°; P6122 (phase III), \(a=\sqrt{3}\)∙a0 \(b=\sqrt{3}\)∙a0 c = 3∙c0 α = 90.0° β = 90.0° γ = 120.0°; B2/n (phase III), \(a=\sqrt{3}\)∙a0 b = 2∙c0 c = 3∙a0 α = 90.0° β = 90.0° γ = 90.0°; Ibam (phase V), \(a=\sqrt{3}\)∙a0 b = a0 c = 2∙c0 α = 90.0° β = 90.0° γ = 90.0°; Pc (phase IV), \(a=\sqrt{3}\)∙a0 b = 3∙a0 c = 2∙c0 α = 90.0° β = 90.0° γ = 90.0°; Cc (phase IV), \(a=2\cdot \sqrt{3}\)∙a0 \(b=2\cdot \sqrt{3}\cdot \)a0 c = 2∙c0 α = 90.0° β = 90.0° γ = 120.0°; Pca21 (phase V) \(a=\sqrt{3}\cdot \)a0 b = 3∙a0 c = 2∙c0 α = 90.0° β = 90.0° γ = 90.0°; P62/c \(a=\sqrt{3}\cdot \)a0 \(b=\sqrt{3}\)∙a0 c = 2∙c0 α = 90.0° β = 90.0° γ = 120.0°; Pna21 (phase V), a = \(2\)∙c0 b = 3∙a0 \(c=\sqrt{3}\)∙a0 α = 90.0° β = 90.0° γ = 90.0°. Atomic coordinates of models from literatures1,26,27,44 were used to calculate XRD patterns. P62/c (phase V) in (d) has very weak (1 0 3) peak, which cannot be displayed in the plotted figure. B2/n is another setting of the so-called C2/c structure with c axis as the unique axis. The calculated intensity of the reflection corresponding to the (1 1 0) of P\(\bar{6}2c\), based on B2/n, is 0.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Ji, C., Li, B., Luo, J. et al. Ultrahigh-pressure crystallographic passage towards metallic hydrogen. Nature 641, 904–909 (2025). https://doi.org/10.1038/s41586-025-08936-w
Received:
Accepted:
Published:
Issue date:
DOI: https://doi.org/10.1038/s41586-025-08936-w
This article is cited by
-
Polymerization of hydrogen: A crucial milestone toward atomic metallic hydrogen
Science China Physics, Mechanics & Astronomy (2025)