Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Traceable random numbers from a non-local quantum advantage

Nature volume 642, pages 916–921 (2025)Cite this article

Subjects

Abstract

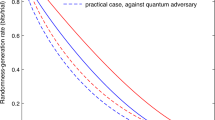
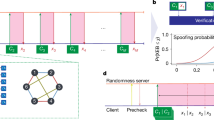
The unpredictability of random numbers is fundamental to both digital security1,2 and applications that fairly distribute resources3,4. However, existing random number generators have limitations—the generation processes cannot be fully traced, audited and certified to be unpredictable. The algorithmic steps used in pseudorandom number generators5 are auditable, but they cannot guarantee that their outputs were a priori unpredictable given knowledge of the initial seed. Device-independent quantum random number generators6,7,8,9 can ensure that the source of randomness was unknown beforehand, but the steps used to extract the randomness are vulnerable to tampering. Here we demonstrate a fully traceable random number generation protocol based on device-independent techniques. Our protocol extracts randomness from unpredictable non-local quantum correlations, and uses distributed intertwined hash chains to cryptographically trace and verify the extraction process. This protocol forms the basis for a public traceable and certifiable quantum randomness beacon that we have launched10. Over the first 40 days of operation, we completed the protocol 7,434 out of 7,454 attempts—a success rate of 99.7%. Each time the protocol succeeded, the beacon emitted a pulse of 512 bits of traceable randomness. The bits are certified to be uniform with error multiplied by actual success probability bounded by 2−64. The generation of certifiable and traceable randomness represents a public service that operates with an entanglement-derived advantage over comparable classical approaches.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Overview of hash chain protocol.
Fig. 2: Experimental set-up.
Fig. 3: Protocol latency.
Fig. 4: Running entropy analysis.

Similar content being viewed by others

Data availability

All data and information used to generate each randomness pulse are publicly available at https://random.colorado.edu. Additional data used for diagnostic plots shown in the Supplementary Information are available by request from the corresponding authors. Source data are provided with this paper.

Code availability

The code used to run the beacon, analyse the data, and verify or trace the randomness in a pulse is publicly available via GitHub at https://github.com/buff-beacon-project. Code used to generate the figures is available by request from the corresponding authors.

References

  1. Buchmann, J. A. Introduction to Cryptography (Springer, 2004).

  2. Eastlake, D. E. 3rd, Crocker, S. & Schiller, J. I. Randomness Requirements for Security. Request for Comments 4086 (Internet Engineering Task Force, 2005).

  3. Stone, P. Why lotteries are just. J. Polit. Philos. 15, 276–295 (2007).

    Article  Google Scholar 

  4. Duxbury, N. Random Justice: On Lotteries and Legal Decision-Making (Oxford Univ. Press, 1999).

  5. Menezes, A. J., Van Oorschot, P. C. & Vanstone, S. A. Handbook of Applied Cryptography 1st edn (CRC, 2018).

  6. Bierhorst, P. et al. Experimentally generated randomness certified by the impossibility of superluminal signals. Nature 556, 223–226 (2018).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  7. Liu, Y. et al. Device-independent quantum random-number generation. Nature 562, 548–551 (2018).

    Article  CAS  PubMed  Google Scholar 

  8. Colbeck, R. Quantum and relativistic protocols for secure multi-party computation. Preprint at https://arxiv.org/abs/0911.3814 (2011).

  9. Pironio, S. et al. Random numbers certified by Bell’s theorem. Nature 464, 1021–1024 (2010).

    Article  CAS  PubMed  Google Scholar 

  10. CURBy CU Randomness Beacon (University of Colorado Boulder, 2024); https://random.colorado.edu/

  11. Bosley, C. & Dodis, Y. in Theory of Cryptography Vol. 4392 (ed. Vadhan, S. P.) 1–20 (Springer, 2007).

  12. Stipčević, M. & Koç, Ç. K. in Open Problems in Mathematics and Computational Science (ed. Koç, Ç. K.) 275–315 (Springer, 2014).

  13. Aaronson, S. & Hung, S.-H. Certified randomness from quantum supremacy. In Proc. 55th Annual ACM Symposium on Theory of Computing (eds Saha, B. & Servedio, R. A.) 933–944 (ACM, 2023).

  14. Koç, Ç. K. (ed.) Cryptographic Engineering (Springer, 2009).

  15. Herrero-Collantes, M. & Garcia-Escartin, J. C. Quantum random number generators. Rev. Mod. Phys. 89, 015004 (2017).

    Article  MathSciNet  Google Scholar 

  16. Rabin, M. O. Transaction protection by beacons. J. Comput. Syst. Sci. 27, 256–267 (1983).

    Article  MathSciNet  Google Scholar 

  17. Kelsey, J., Brandão, L. T. A. N., Peralta, R. & Booth, H. A reference for randomness beacons. Preprint at https://doi.org/10.6028/NIST.IR.8213-draft (2019).

  18. Bonneau, J., Clark, J. & Goldfeder, S. On bitcoin as a public randomness source. Preprint at https://eprint.iacr.org/2015/1015 (2015).

  19. Syta, E. et al. Scalable bias-resistant distributed randomness. In Proc. 2017 IEEE Symposium on Security and Privacy (SP) (ed. Butler, K. R. B.) 444–460 (IEEE, 2017).

  20. Fischer, M. J., Iorga, M. & Peralta, R. A public randomness service. In Proc. International Conference on Security and Cryptography (eds Lopez, J. & Samarati, P.) 434–438 (IEEE, 2011).

  21. Micali, S., Rabin, M. & Vadhan, S. Verifiable random functions. In Proc. 40th Annual Symposium on Foundations of Computer Science (Cat. No.99CB37039) (ed. Mitsenmacher, M.) 120–130 (IEEE, 1999).

  22. Gras, G., Martin, A., Choi, J. W. & Bussières, F. Quantum entropy model of an integrated quantum-random-number-generator chip. Phys. Rev. Appl. 15, 054048 (2021).

    Article  CAS  Google Scholar 

  23. Abellán, C., Amaya, W., Mitrani, D., Pruneri, V. & Mitchell, M. W. Generation of fresh and pure random numbers for loophole-free Bell tests. Phys. Rev. Lett. 115, 250403 (2015).

    Article  PubMed  Google Scholar 

  24. Soucarros, M., Canovas-Dumas, C., Clediere, J., Elbaz-Vincent, P. & Real, D. Influence of the temperature on true random number generators. In Proc. 2011 IEEE International Symposium on Hardware-Oriented Security and Trust (eds Schaumont, P. & Karri, R.) 24–27 (IEEE, 2011).

  25. Ragab, H., Milburn, A., Razavi, K., Bos, H. & Giuffrida, C. Crosstalk: speculative data leaks across cores are real. In Proc. 2021 IEEE Symposium on Security and Privacy (SP) (eds Oprea, A. & Holz, T.) 1852–1867 (IEEE, 2021).

  26. Shalm, L. K. et al. Device-independent randomness expansion with entangled photons. Nat. Phys. 17, 452–456 (2021).

    Article  CAS  Google Scholar 

  27. Li, M.-H. et al. Experimental realization of device-independent quantum randomness expansion. Phys. Rev. Lett. 126, 050503 (2021).

    Article  CAS  PubMed  Google Scholar 

  28. Liu, W.-Z. et al. Device-independent randomness expansion against quantum side information. Nat. Phys. 17, 448–451 (2021).

    Article  Google Scholar 

  29. Shalm, L. K. et al. Strong loophole-free test of local realism. Phys. Rev. Lett. 115, 250402 (2015).

    Article  PubMed  PubMed Central  Google Scholar 

  30. Giustina, M. et al. Significant-loophole-free test of Bell’s theorem with entangled photons. Phys. Rev. Lett. 115, 250401 (2015).

    Article  PubMed  Google Scholar 

  31. Hensen, B. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).

    Article  CAS  PubMed  Google Scholar 

  32. Rosenfeld, W. et al. Event-ready Bell test using entangled atoms simultaneously closing detection and locality loopholes. Phys. Rev. Lett. 119, 010402 (2017).

    Article  PubMed  Google Scholar 

  33. Storz, S. et al. Loophole-free Bell inequality violation with superconducting circuits. Nature 617, 265–270 (2023).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  34. Zhang, Y., Knill, E. & Bierhorst, P. Certifying quantum randomness by probability estimation. Phys. Rev. A 98, 040304 (2018).

    Article  Google Scholar 

  35. Dupuis, F., Fawzi, O. & Renner, R. Entropy accumulation. Commun. Math. Phys. 379, 867–913 (2020).

    Article  MathSciNet  Google Scholar 

  36. Ma, X. et al. Postprocessing for quantum random-number generators: entropy evaluation and randomness extraction. Phys. Rev. A 87, 062327 (2013).

    Article  Google Scholar 

  37. Trevisan, L. Extractors and pseudorandom generators. J. ACM 48, 860–879 (2001).

    Article  MathSciNet  Google Scholar 

  38. Mauerer, W., Portmann, C. & Scholz, V. B. A modular framework for randomness extraction based on Trevisan’s construction. Preprint at https://arxiv.org/abs/1212.0520 (2012).

  39. Zhang, Y. et al. Experimental low-latency device-independent quantum randomness. Phys. Rev. Lett. 124, 010505 (2020).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  40. Lamport, L. Password authentication with insecure communication. Commun. ACM 24, 770–772 (1981).

    Article  Google Scholar 

  41. Dworkin, M. J. SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions. Technical Report NIST FIPS 202 (National Institute of Standards and Technology, 2015).

  42. Cormen, T. H., Leiserson, C. E., Rivest, R. L. & Stein, C. Introduction to Algorithms 3rd edn (MIT Press, 2009).

  43. Thulasiraman, K. & Swamy, M. N. S. Graphs: Theory and Algorithms (Wiley, 2011).

  44. Gailly, N. et al. drand/drand: A Distributed Randomness Beacon Daemon - Go implementation. GitHub https://github.com/drand/drand (2024).

  45. Grassi, P. A., Garcia, M. E. & Fenton, J. L. Digital Identity Guidelines: Revision 3. Technical Report NIST SP 800-63-3 (National Institute of Standards and Technology, 2017).

  46. Benet, J. IPFS - content addressed, versioned, P2P file system, Preprint at https://arxiv.org/abs/1407.3561 (2014).

  47. Reddy, D. V., Nerem, R. R., Nam, S. W., Mirin, R. P. & Verma, V. B. Superconducting nanowire single-photon detectors with 98% system detection efficiency at 1550 nm. Optica 7, 1649–1653 (2020).

    Article  Google Scholar 

  48. Dowling, J. P. & Milburn, G. J. Quantum technology: the second quantum revolution. Philos. Trans. R. Soc. A 361, 1655–1674 (2003).

    Article  MathSciNet  Google Scholar 

  49. Chambers, C. D. & Tzavella, L. The past, present and future of Registered Reports. Nat. Hum. Behav. 6, 29–42 (2021).

    Article  PubMed  Google Scholar 

  50. Gheorghiu, A. & Vidick, T. Computationally-secure and composable remote state preparation. In Proc. 2019 IEEE 60th Annual Symposium on Foundations of Computer Science (FOCS) (ed. Zuckerman, D.) 1024–1033 (2019).

  51. Cojocaru, A., Colisson, L., Kashefi, E. & Wallden, P. QFactory: classically-instructed remote secret qubits preparation. In Proc. Advances in Cryptology – ASIACRYPT 2019 (eds Galbraith, S. D. & Moriai, S.) 615–645 (Springer, 2019).

  52. Mahadev, U. Classical verification of quantum computations. In Proc. 2018 IEEE 59th Annual Symposium on Foundations of Computer Science (FOCS) 259–267 (IEEE, 2018).

  53. Zhu, D. et al. Interactive cryptographic proofs of quantumness using mid-circuit measurements. Nat. Phys. 19, 1725–1731 (2023).

    Article  CAS  Google Scholar 

  54. Brakerski, Z., Christiano, P., Mahadev, U., Vazirani, U. & Vidick, T.A cryptographic test of quantumness and certifiable randomness from a single quantum device. J. ACM 68, 31 (2021).

Download references

Acknowledgements

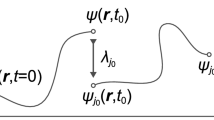
This work includes contributions of the NIST, which are not subject to US copyright. The use of trade names does not imply endorsement by the US Government. The work is supported by the National Science Foundation RAISE-TAQS programme (award 1840223), the CU through the ‘QuEST Seed Award: A Quantum Randomness Beacon’, the Colorado Office of Economic Impact (award number DO 2023-0335), in part by the European Union ‘NextGenerationEU/PRTR’. Spanish Ministry of Science MCIN: project SAPONARIA (PID2021-123813NB-I00) and ‘Severo Ochoa’ Center of Excellence CEX2019-000910-S. Generalitat de Catalunya through the CERCA programme and grant number 2021 SGR 01453; Fundació Privada Cellex; Fundació Mir-Puig. This work was performed in part at Oak Ridge National Laboratory, operated by UT-Battelle for the US Department of Energy under contract number DE-AC05-00OR22725. We thank S. Glancy, B. Chen, L. Norton, E. Some and R. Snyder for discussions regarding the project, and J. G. Price for providing the image used in Fig. 2.

Author information

Author notes

  1. Joseph M. Cavanagh

    Present address: Pitzer Center for Theoretical Chemistry, Department of Chemistry, University of California, Berkeley, CA, USA

Authors and Affiliations

  1. Department of Physics, University of Colorado, Boulder, CO, USA

    Gautam A. Kavuri, Jasper Palfree, Dileep V. Reddy, Michael D. Mazurek, Paul D. Beale, Sae Woo Nam, Emanuel Knill & Lynden K. Shalm

  2. Physical Measurement Laboratory, National Institute of Standards and Technology, Boulder, CO, USA

    Gautam A. Kavuri, Jasper Palfree, Dileep V. Reddy, Michael D. Mazurek, Joseph M. Cavanagh, Aagam Dalal, Sae Woo Nam, Richard P. Mirin, Martin J. Stevens & Lynden K. Shalm

  3. Quantum Information Science Section, Computational Sciences and Engineering Division, Oak Ridge National Laboratory, Oak Ridge, TN, USA

    Yanbao Zhang

  4. Joint Quantum Institute, National Institute of Standards and Technology and University of Maryland, Gaithersburg, MD, USA

    Joshua C. Bienfang

  5. Center for Quantum Information and Control, University of New Mexico, Albuquerque, NM, USA

    Mohammad A. Alhejji

  6. Department of Electrical, Computer, and Energy Engineering, University of Colorado, Boulder, CO, USA

    Aliza U. Siddiqui

  7. Quside Technologies, Barcelona, Spain

    Carlos Abellán & Waldimar Amaya

  8. ICFO-Institut de Ciencies Fotoniques, The Barcelona Institute of Science and Technology, Barcelona, Spain

    Morgan W. Mitchell

  9. ICREA - Institució Catalana de Recerca i Estudis Avançats, Barcelona, Spain

    Morgan W. Mitchell

  10. Department of Mathematics, University of Colorado, Boulder, CO, USA

    Katherine E. Stange

  11. Strativia (NIST Cryptographic Technology Group), Gaithersburg, MD, USA

    Luís T. A. N. Brandão

  12. Information Technology Laboratory, National Institute of Standards and Technology, Gaithersburg, MD, USA

    Harold Booth & René Peralta

  13. Center for Theory of Quantum Matter, University of Colorado, Boulder, CO, USA

    Emanuel Knill

  14. Applied and Computational Mathematics Division, National Institute of Standards and Technology, Boulder, CO, USA

    Emanuel Knill

  15. Quantum Engineering Initiative, Department of Electrical, Computer, and Energy Engineering, University of Colorado, Boulder, CO, USA

    Lynden K. Shalm

Authors
  1. Gautam A. Kavuri
    View author publications

    Search author on:PubMed Google Scholar

  2. Jasper Palfree
    View author publications

    Search author on:PubMed Google Scholar

  3. Dileep V. Reddy
    View author publications

    Search author on:PubMed Google Scholar

  4. Yanbao Zhang
    View author publications

    Search author on:PubMed Google Scholar

  5. Joshua C. Bienfang
    View author publications

    Search author on:PubMed Google Scholar

  6. Michael D. Mazurek
    View author publications

    Search author on:PubMed Google Scholar

  7. Mohammad A. Alhejji
    View author publications

    Search author on:PubMed Google Scholar

  8. Aliza U. Siddiqui
    View author publications

    Search author on:PubMed Google Scholar

  9. Joseph M. Cavanagh
    View author publications

    Search author on:PubMed Google Scholar

  10. Aagam Dalal
    View author publications

    Search author on:PubMed Google Scholar

  11. Carlos Abellán
    View author publications

    Search author on:PubMed Google Scholar

  12. Waldimar Amaya
    View author publications

    Search author on:PubMed Google Scholar

  13. Morgan W. Mitchell
    View author publications

    Search author on:PubMed Google Scholar

  14. Katherine E. Stange
    View author publications

    Search author on:PubMed Google Scholar

  15. Paul D. Beale
    View author publications

    Search author on:PubMed Google Scholar

  16. Luís T. A. N. Brandão
    View author publications

    Search author on:PubMed Google Scholar

  17. Harold Booth
    View author publications

    Search author on:PubMed Google Scholar

  18. René Peralta
    View author publications

    Search author on:PubMed Google Scholar

  19. Sae Woo Nam
    View author publications

    Search author on:PubMed Google Scholar

  20. Richard P. Mirin
    View author publications

    Search author on:PubMed Google Scholar

  21. Martin J. Stevens
    View author publications

    Search author on:PubMed Google Scholar

  22. Emanuel Knill
    View author publications

    Search author on:PubMed Google Scholar

  23. Lynden K. Shalm
    View author publications

    Search author on:PubMed Google Scholar

Contributions

G.A.K. built and performed the experiment with assistance from L.K.S., M.D.M. and M.J.S., and collected and analysed data. J.P. and L.K.S. developed the Twine protocol with inputs from L.T.A.N.B., H.B. and R.P., and implemented it with assistance from J.M.C. and A.D. D.V.R. provided the high-efficiency detectors. Y.Z., M.A.A., A.U.S., L.K.S., G.A.K. and E.K. participated in the data analysis. J.C.B. provided electronics and hardware RNGs. C.A., W.A. and M.W.M. provided hardware RNGs. P.D.B. and J.P. developed a software RNG used in CURBy. J.P., K.E.S., L.K.S. and P.D.B. developed the hardware and software at CU to run the CURBy network. L.K.S., S.W.N. and R.P.M. supervised the project. G.A.K. led the writing of the manuscript with all authors contributing.

Corresponding authors

Correspondence to Gautam A. Kavuri or Lynden K. Shalm.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Source data

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kavuri, G.A., Palfree, J., Reddy, D.V. et al. Traceable random numbers from a non-local quantum advantage. Nature 642, 916–921 (2025). https://doi.org/10.1038/s41586-025-09054-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41586-025-09054-3

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing