Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

A soft-clamped topological waveguide for phonons

Nature volume 642, pages 947–953 (2025)Cite this article

Subjects

Abstract

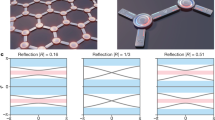
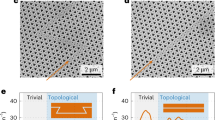
Topological insulators were originally discovered for electron waves in condensed-matter systems. Recently, this concept has been transferred to bosonic systems such as photons1 and phonons2, which propagate in materials patterned with artificial lattices that emulate spin-Hall physics. This work has been motivated, in part, by the prospect of topologically protected transport along edge channels in on-chip circuits2,3. In principle, topology protects propagation against backscattering, but not against loss, which has remained limited to the dB cm−1 level for phononic waveguides, whether topological4,5,6,7 or not8,9,10,11,12,13,14,15,16,17,18,19. Here we combine advanced dissipation engineering20—in particular, the recently introduced method of soft clamping21—with the concept of valley-Hall topological insulators for phonons22,23,24,25,26. This enables on-chip phononic waveguides with propagation losses due to dissipation of 3 dB km−1 at room temperature, orders of magnitude below any previous chip-scale devices. The low losses also allow us to accurately quantify backscattering protection in topological phononic waveguides, using high-resolution ultrasound spectroscopy. We infer that phonons follow a sharp, 120° bend with a 99.99% probability instead of being scattered back, and less than one phonon in a million is lost. Our work will inspire new research directions on ultralow-loss phononic waveguides and will provide a clean bosonic system for investigating topological protection and non-Hermitian topological physics.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: A topological waveguide for phonons with ultralow loss.
Fig. 2: Valley-Hall topological insulators and edge states in a thin stressed membrane.
Fig. 3: Triangular-waveguide phononic cavities with ultralow loss.
Fig. 4: Backscattering-induced mode splitting.
Fig. 5: Parametric amplification and damping.

Similar content being viewed by others

Data availability

The data that support the findings of this study in the main text and the Supplementary Information are available at Zenodo53 (https://doi.org/10.5281/zenodo.15183532).

Code availability

The codes that support the findings of this study are available at Zenodo53 (https://doi.org/10.5281/zenodo.15183532).

References

  1. Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2019).

    Article  MathSciNet  CAS  Google Scholar 

  2. Shah, T., Brendel, C., Peano, V. & Marquardt, F. Colloquium: topologically protected transport in engineered mechanical systems. Rev. Mod. Phys. 96, 021002 (2024).

    Article  Google Scholar 

  3. Hafezi, M., Demler, E. A., Lukin, M. D. & Taylor, J. M. Robust optical delay lines with topological protection. Nat. Phys. 7, 907–912 (2011).

    Article  CAS  Google Scholar 

  4. Cha, J., Kim, K. W. & Daraio, C. Experimental realization of on-chip topological nanoelectromechanical metamaterials. Nature 564, 229–233 (2018).

    Article  CAS  PubMed  Google Scholar 

  5. Yu, S.-Y. et al. Critical couplings in topological-insulator waveguide-resonator systems observed in elastic waves. Natl Sci. Rev. 8, nwaa262 (2020).

    Article  PubMed  PubMed Central  Google Scholar 

  6. Xi, X., Ma, J., Wan, S., Dong, C.-H. & Sun, X. Observation of chiral edge states in gapped nanomechanical graphene. Sci. Adv. 7, eabe1398 (2021).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  7. Hatanaka, D. et al. Valley pseudospin polarized evanescent coupling between microwave ring resonator and waveguide in phononic topological insulators. Nano Lett. 24, 5570–5577 (2024).

    Article  CAS  PubMed  Google Scholar 

  8. Hatanaka, D., Mahboob, I., Onomitsu, K. & Yamaguchi, H. Phonon waveguides for electromechanical circuits. Nat. Nanotechnol. 9, 520–524 (2014).

    Article  CAS  PubMed  Google Scholar 

  9. Hatanaka, D., Dodel, A., Mahboob, I., Onomitsu, K. & Yamaguchi, H. Phonon propagation dynamics in band-engineered one-dimensional phononic crystal waveguides. New J. Phys. 17, 113032 (2015).

    Article  Google Scholar 

  10. Cha, J. & Daraio, C. Electrical tuning of elastic wave propagation in nanomechanical lattices at MHz frequencies. Nat. Nanotechnol. 13, 1016–1020 (2018).

    Article  CAS  PubMed  Google Scholar 

  11. Fu, W. et al. Phononic integrated circuitry and spin-orbit interaction of phonons. Nat. Commun. 10, 2743 (2019).

    Article  PubMed  PubMed Central  Google Scholar 

  12. Patel, R. N. et al. Single-mode phononic wire. Phys. Rev. Lett. 121, 040501 (2018).

    Article  CAS  PubMed  Google Scholar 

  13. Romero, E. et al. Propagation and imaging of mechanical waves in a highly stressed single-mode acoustic waveguide. Phys. Rev. Appl. 11, 064035 (2019).

    Article  CAS  Google Scholar 

  14. Mayor, F. M. et al. Gigahertz phononic integrated circuits on thin-film lithium niobate on sapphire. Phys. Rev. Appl. 15, 014039 (2021).

    Article  CAS  Google Scholar 

  15. Xu, X.-B. et al. High-frequency traveling-wave phononic cavity with sub-micron wavelength. Appl. Phys. Lett. 120, 163503 (2022).

    Article  CAS  Google Scholar 

  16. Feng, Z., Liu, Y., Xi, X., Wang, L. & Sun, X. Gigahertz phononic integrated circuits based on overlay slot waveguides. Phys. Rev. Appl. 19, 064076 (2023).

    Article  CAS  Google Scholar 

  17. Chen, I.-T. et al. Optomechanical ring resonator for efficient microwave-optical frequency conversion. Nat. Commun. 14, 7594 (2023).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  18. Zhang, L., Cui, C., Chen, P.-K. & Fan, L. Integrated-waveguide-based acousto-optic modulation with complete optical conversion. Optica 11, 184–189 (2024).

    Article  CAS  Google Scholar 

  19. Bicer, M. & Balram, K. C. Low-loss GHz frequency phononic integrated circuits in gallium nitride for compact radio frequency acoustic wave devices. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 71, 172–181 (2024).

    Article  PubMed  Google Scholar 

  20. Engelsen, N. J., Beccari, A. & Kippenberg, T. J. Ultrahigh-quality-factor micro- and nanomechanical resonators using dissipation dilution. Nat. Nanotechnol. 19, 725–737 (2024).

    Article  CAS  PubMed  Google Scholar 

  21. Tsaturyan, Y., Barg, A., Polzik, E. S. & Schliesser, A. Ultracoherent nanomechanical resonators via soft clamping and dissipation dilution. Nat. Nanotechnol. 12, 776–783 (2017).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  22. Lu, J. et al. Observation of topological valley transport of sound in sonic crystals. Nat. Phys. 13, 369–374 (2017).

    Article  CAS  Google Scholar 

  23. Yan, M. et al. On-chip valley topological materials for elastic wave manipulation. Nat. Mater. 17, 993–998 (2018).

    Article  CAS  PubMed  Google Scholar 

  24. Ma, J., Xi, X. & Sun, X. Experimental demonstration of dual-band nano-electromechanical valley-hall topological metamaterials. Adv. Mater. 33, 2006521 (2021).

    Article  CAS  Google Scholar 

  25. Zhang, Q. et al. Gigahertz topological valley Hall effect in nanoelectromechanical phononic crystals. Nat. Electron. 5, 157–163 (2022).

    Article  CAS  Google Scholar 

  26. Ren, H. et al. Topological phonon transport in an optomechanical system. Nat. Commun. 13, 3476 (2022).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  27. Eggleton, B. J., Poulton, C. G., Rakich, P. T., Steel, M. J. & Bahl, G. Brillouin integrated photonics. Nat. Photon. 13, 664–677 (2019).

    Article  CAS  Google Scholar 

  28. Safavi-Naeini, A. H., van Thourhout, D., Baets, R. & Laer, R.van Controlling phonons and photons at the wavelength scale: integrated photonics meets integrated phononics. Optica 6, 213–232 (2019).

    Article  CAS  Google Scholar 

  29. Fang, K., Matheny, M. H., Luan, X. & Painter, O. Optical transduction and routing of microwave phonons in cavity-optomechanical circuits. Nat. Photon. 10, 489–496 (2016).

    Article  CAS  Google Scholar 

  30. Zivari, A., Stockill, R., Fiaschi, N. & Gröblacher, S. Non-classical mechanical states guided in a phononic waveguide. Nat. Phys. 18, 789–793 (2022).

    Article  CAS  Google Scholar 

  31. Wu, L.-H. & Hu, X. Scheme for achieving a topological photonic crystal by using dielectric material. Phys. Rev. Lett. 114, 223901 (2015).

    Article  PubMed  Google Scholar 

  32. Khanikaev, A. B. & Shvets, G. Two-dimensional topological photonics. Nat. Photon. 11, 763–773 (2017).

    Article  CAS  Google Scholar 

  33. Barik, S. et al. A topological quantum optics interface. Science 359, 666–668 (2018).

    Article  MathSciNet  CAS  PubMed  Google Scholar 

  34. Cupertino, A. et al. Centimeter-scale nanomechanical resonators with low dissipation. Nat. Commun. 15, 4255 (2024).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  35. Rossi, M., Mason, D., Chen, J., Tsaturyan, Y. & Schliesser, A. Measurement-based quantum control of mechanical motion. Nature 563, 53–58 (2018).

    Article  CAS  PubMed  Google Scholar 

  36. Mason, D., Chen, J., Rossi, M., Tsaturyan, Y. & Schliesser, A. Continuous force and displacement measurement below the standard quantum limit. Nat. Phys. 15, 745–749 (2019).

    Article  CAS  Google Scholar 

  37. Huang, G., Beccari, A., Engelsen, N. J. & Kippenberg, T. J. Room-temperature quantum optomechanics using an ultralow noise cavity. Nature 626, 512–516 (2024).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  38. Seis, Y. et al. Ground state cooling of an ultracoherent electromechanical system. Nat. Commun. 13, 1507 (2022).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  39. Kurpiers, P., Walter, T., Magnard, P., Salathe, Y. & Wallraff, A. Characterizing the attenuation of coaxial and rectangular microwave-frequency waveguides at cryogenic temperatures. EPJ Quantum Technol. 4, 8 (2017).

    Article  PubMed  PubMed Central  Google Scholar 

  40. Schmid, S., Villanueva, L. G. & Roukes, M. L. Fundamentals of Nanomechanical Resonators 2nd edn (Springer, 2023).

  41. Košata, J. & Zilberberg, O. Second-order topological modes in two-dimensional continuous media. Phys. Rev. Res. 3, L032029 (2021).

    Article  Google Scholar 

  42. Lu, J. et al. Dirac cones in two-dimensional artificial crystals for classical waves. Phys. Rev. B 89, 134302 (2014).

    Article  Google Scholar 

  43. Shah, T., Marquardt, F. & Peano, V. Tunneling in the Brillouin zone: theory of backscattering in valley Hall edge channels. Phys. Rev. B 104, 235431 (2021).

    Article  CAS  Google Scholar 

  44. Villanueva, L. G. & Schmid, S. Evidence of surface loss as ubiquitous limiting damping mechanism in sin micro- and nanomechanical resonators. Phys. Rev. Lett. 113, 227201 (2014).

    Article  CAS  PubMed  Google Scholar 

  45. Rempe, G., Thomson, R. J., Kimble, H. J. & Lalezari, R. Measurement of ultralow losses in an optical interferometer. Opt. Lett. 17, 363–365 (1992).

    Article  CAS  PubMed  Google Scholar 

  46. Rosiek, C. A. et al. Observation of strong backscattering in valley-Hall photonic topological interface modes. Nat. Photon. 17, 386–392 (2023).

    Article  CAS  Google Scholar 

  47. Rugar, D. & Grütter, P. Mechanical parametric amplification and thermomechanical noise squeezing. Phys. Rev. Lett. 67, 699–702 (1991).

    Article  CAS  PubMed  Google Scholar 

  48. Xi, X., Ma, J. & Sun, X. A topological parametric phonon oscillator. Adv. Mater. 37, 2309015 (2025).

    Article  CAS  PubMed  Google Scholar 

  49. Peano, V., Houde, M., Marquardt, F. & Clerk, A. A. Topological quantum fluctuations and traveling wave amplifiers. Phys. Rev. X 6, 041026 (2016).

    Google Scholar 

  50. Hälg, D. et al. Strong parametric coupling between two ultracoherent membrane modes. Phys. Rev. Lett. 128, 094301 (2022).

    Article  PubMed  Google Scholar 

  51. Barg, A. et al. Measuring and imaging nanomechanical motion with laser light. Appl. Phys. B 123, 8 (2017).

    Article  PubMed  Google Scholar 

  52. Mashaal, A. et al. Strong thermomechanical noise squeezing stabilized by feedback. Phys. Rev. Res. 7, L012071 (2025).

    Article  CAS  Google Scholar 

  53. Xi, X. et al. Data and code for “A soft-clamped topological waveguide for phonons”. Zenodo https://doi.org/10.5281/zenodo.15183532 (2025).

Download references

Acknowledgements

We acknowledge T. Capelle for the help with micro-fabrication. This work was supported by the European Research Council project PHOQS (grant no. 101002179), the Novo Nordisk Foundation (grant nos. NNF20OC0061866 and NNF22OC0077964), the Danish National Research Foundation (Centre of Excellence ‘Hy-Q’), the Independent Research Fund Denmark (grant no. 1026-00345B), the Swiss National Science Foundation (CRSII5 177198/1, CRSII5 206008/1 and PP00P2 163818), the Deutsche Forschungsgemeinschaft (project nos. 449653034 and SFB1432), the Horizon 2020 research and innovation programme of the European Union (the Marie Skłodowska–Curie grant agreement no. 101107341) and a research grant (VIL59143) from the Villum Foundation.

Author information

Author notes

  1. Jan Košata

    Present address: Hitachi Energy Research, Baden-Dättwil, Switzerland

Authors and Affiliations

  1. Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark

    Xiang Xi, Ilia Chernobrovkin, Mads B. Kristensen, Eric Langman, Anders S. Sørensen & Albert Schliesser

  2. Center for Hybrid Quantum Networks, Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark

    Xiang Xi, Ilia Chernobrovkin, Mads B. Kristensen, Eric Langman, Anders S. Sørensen & Albert Schliesser

  3. Institute for Theoretical Physics, ETH Zürich, Zurich, Switzerland

    Jan Košata

  4. Department of Physics, University of Konstanz, Konstanz, Germany

    Oded Zilberberg

Authors
  1. Xiang Xi
    View author publications

    Search author on:PubMed Google Scholar

  2. Ilia Chernobrovkin
    View author publications

    Search author on:PubMed Google Scholar

  3. Jan Košata
    View author publications

    Search author on:PubMed Google Scholar

  4. Mads B. Kristensen
    View author publications

    Search author on:PubMed Google Scholar

  5. Eric Langman
    View author publications

    Search author on:PubMed Google Scholar

  6. Anders S. Sørensen
    View author publications

    Search author on:PubMed Google Scholar

  7. Oded Zilberberg
    View author publications

    Search author on:PubMed Google Scholar

  8. Albert Schliesser
    View author publications

    Search author on:PubMed Google Scholar

Contributions

X.X. designed the devices and built the setup with contributions from I.C.; X.X. and I.C. conducted the measurements and analysed the data. J.K. and O.Z. contributed to the design at an early stage and developed the topological theory. X.X., J.K., M.B.K. and E.L. conducted the numerical simulations. X.X., M.B.K. and A.S. analysed dissipation dilution and soft clamping. E.L. fabricated the devices. A.S.S. contributed to the discussion and understanding of the experimental data. X.X., J.K. and A.S. wrote the paper with input from all the authors. X.X. and A.S. supervised the project.

Corresponding authors

Correspondence to Xiang Xi or Albert Schliesser.

Ethics declarations

Competing interests

E.L. and A.S. have co-founded the company Qfactory ApS, which commercializes soft-clamped phononic resonators. The other authors declare no competing interests.

Peer review

Peer review information

Nature thanks Jiuyang Lu and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data figures and tables

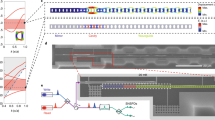
Extended Data Fig. 1 Experimental setup.

Shown is the fiber laser (1550 nm), the two photodetectors (PD), the proportional-integral-derivative (PID) controller (FPGA: Red Pitaya), a phase shifter (θ, piezo fiber stretcher), the lock-in amplifier (lock-in), and a signal generator (SG). The membrane is simultaneously imaged with a CCD camera.

Supplementary information

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xi, X., Chernobrovkin, I., Košata, J. et al. A soft-clamped topological waveguide for phonons. Nature 642, 947–953 (2025). https://doi.org/10.1038/s41586-025-09092-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41586-025-09092-x

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing