Main

Learning is a fundamental process driving adaptability and survival across biological scales. At the organismal level, neural rewiring and synaptic plasticity enable the brain to learn and form memories, essential for behavioural adaptation and decision-making8. At the cellular level and in a simpler form, the immune system learns from pathogen encounters, enhancing future responses9. At the molecular level and in the simplest form, biochemical circuits in bacteria learn about their environment, forming short-term memories to optimize survival10.

Inspired by these natural processes, researchers have explored the deep connections between biological learning algorithms and engineered cellular and molecular networks in numerous theoretical and experimental studies11,12,13. These studies span a diverse range of systems, including abstract chemical reaction networks14,15,16, genetic regulatory networks17,18,19, protein circuits7,20 and metabolic circuits21. Notably, DNA-based systems such as cell-free transcriptional and translational circuits22,23, polymerase-exonuclease-nickase DNA circuits6,24, DNA strand-displacement circuits3,4,5,24,25 and DNA tile self-assembly26 have been developed to perform molecular pattern recognition and classification.

Despite three decades of engineering research, experimental demonstrations have been limited to simple adaptive behaviours in systems with no more than a dozen signals27,28,29. The goal of this work is to implement a molecular system that can autonomously learn to perform complex information-processing tasks. To distinguish learning from simple adaptation, consider a future artificial cell that learns from a more advanced entity, such as a biological cell. It observes the teacher’s behaviour, remembers how the teacher responds to a stimuli, learns from multiple examples over time, and generalizes this knowledge to respond independently to similar stimuli. Developing such a system requires several features. First, the artificial cell must interpret molecular inputs on its own, without relying on an instructor to translate between formats—so training and test data must share the same molecular ‘language’ (independence). Second, it must remember new examples without overwriting past memories, integrating all training data presented sequentially (integration). Third, it must generalize from examples, processing test data that differ from training data using a general-purpose architecture for complex and noisy information (generality). Fourth, it must retain long-term memories, making appropriate decisions even days or months after training data are removed (stability). Fifth, its success should be judged by its ability to correctly classify test data given sufficient training examples (accuracy). Sixth, its performance should be enhanced by its ability to process sequential test data and update its decisions over time (reusability). Finally, its power depends on the type of information that it can store and process (flexibility).

We demonstrate a DNA-based molecular system with learning capabilities that satisfy four key features—independence, integration, generality and stability. Stability arises naturally from the DNA implementation, and generality builds on previous work4, whereas independence and integration require substantial engineering, as we will discuss in this paper. The remaining features—accuracy, reusability and flexibility—are not fully met and represent goals for future work (Extended Data Fig. 1).

Concept and design

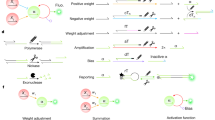
In silico learning produces a DNA neural network with fixed memories—acting like a hardwired processor. In contrast, in vitro learning enables the liquid system itself to form memories in response to example molecular inputs during a training phase—acting like an adaptive memory device. When composed together with a processor, this integrated system provides learned input–output functions applied to a subsequent testing phase (Extended Data Fig. 2). In previous work, we introduced a simple in silico learning algorithm using averaged training patterns as weights for winner-take-all computation4. Here we implement a variant for in vitro learning by molecules within a DNA neural network (Fig. 1a). Initially, all weights are zero, representing a blank memory. During training, input patterns and class labels collectively activate specific weights, adding the input to the corresponding memory. After all examples are presented, the resulting weights—encoded in the concentrations of activator molecules—passively store aggregated training data. Learning transitions to testing by connecting the memory device to the processor, transferring information from activators to weight molecules. These now-active weights interact with test inputs, compute weighted sums for each output and trigger a winner-take-all competition. The output with the largest sum is amplified, producing binary signals that classify the input based on its similarity to the learned memories (Fig. 1b).

Fig. 1: Concept and design of supervised learning in DNA neural networks.
figure 1

a, Abstract training and testing process. b, Example of learning two 9-bit patterns ‘L’ and ‘T’ followed by classification of two corrupted tests. x1 to xn and y1 to y2 are binary inputs and outputs, respectively, represented by coloured and greyscale nodes. Black and white nodes represent outputs that are computed as ON and OFF, respectively. xv = {x1, x2, …, xn} can be either a training or test pattern, shown as a mixture of molecules in a droplet (actual form in an experiment) or arranged in a \(\sqrt{n}\)-by-\(\sqrt{n}\) array for visual clarity. A total of q and p patterns are used for training and testing, respectively. qj is the total number of training patterns in class j. l1 and l2 are binary class labels represented by polygon shapes. aj = {a1,j, a2,j, …, an,j} is a learned memory associated with output yj, which equals the average of all training patterns in class j. After training, the value of aj can then be transferred to wj for classification of test patterns. Light grey and black wires indicate inhibited and activated weights with zero and learned values, respectively. sj is the weighted sum of inputs for comparing a test pattern with memory j, represented by a polygon-shaped node matching the class label. c, Chemical reaction network implementation. d, Seesaw DNA circuit implementation. Black species indicate molecules whose concentrations correspond to variable values in the abstract mathematical function. Grey species indicate molecules designed to facilitate the desired reactions; their concentrations are typically in excess. Threshold thi is used to clean up noise in xi so that the input is only considered ON if xi > thi. For implementation reasons, the computation of weighted sum is split into weight multiplication pi,j = wi,jxi and summation \({s}_{j}={\sum }_{i=1}^{n}{p}_{i,j}\). The ON value of the output is set by the restoration gate concentration gj. kf and ks are reaction rate constants that must satisfy kf ≫ ks in a pair of reactions with shared reactants; separate reactions labelled with kf or ks do not need to have identical rates. Label inhibitor Inhj is not initially present during training but added after each training event to clean up leftover label. Notations for the seesaw circuit diagram are explained in Extended Data Fig. 2 caption.

Full size image

The training process resembles ‘learning by memorizing’, conceptually akin to Hebbian learning30 and k-means clustering31 (‘Learning algorithm’ in Methods). Unlike modern machine learning, which relies on loss functions and optimization, our approach is simpler yet effective for molecular systems. Although it does not extend naturally to deeper neural networks, it provides an initial step for exploring more advanced architectures.

To implement the learning and testing algorithm with molecules, we first translate the abstract mathematical function into a set of chemical reactions, where each variable is represented by the concentration of a chemical species (Fig. 1c). These reactions are then realized using DNA strand displacement32. Although arbitrary chemical reaction networks can be implemented in principle33, experimental demonstrations have been limited to small systems with a few reactions34,35. Simpler schemes such as the seesaw motif36 have enabled larger systems with hundreds of reactions3,4,37,38. Here, inspired by activatable species used in adaptive DNA circuits25,27,39, we extend the seesaw architecture with two new activatable gate motifs (Extended Data Fig. 3) to implement the learning chemical neural network (Fig. 1d and ‘Implementation of learning and testing’ in Methods).

Motif characterization

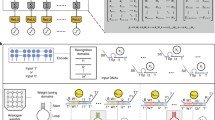
The first motif is an activatable amplification gate (Extended Data Fig. 3). Using this motif, we developed a weight gate that catalytically produces a weighted input signal Pi,j, consisting of a toehold ‘T’ flanked by two long domains Xi and Pj (Fig. 2a). To activate a specific weight Wi,j, the activator Acti,j must carry both input bit (i) and memory class (j) information. Although this could be encoded using two consecutive toeholds via the allosteric toehold mechanism40, that design has drawbacks (‘Alternative activatable weight design’ in Methods). Instead, we encode class information in toehold Tj and bit information in branch migration domain Ai (Fig. 2a). An activator with matching Tj and Ai binds to the inhibited weight \({W}_{i,j}^{* }\), exposing a universal toehold U* for input binding. To embed a hidden thermodynamic drive41, we introduce a bulge loop B between U and Xi in the weight gate’s top strand, with the activator carrying B*. Bulge elimination in branch migration lowers the reverse rate and prolongs U* exposure, enhancing input binding.

Fig. 2: Characterization of key motifs.
figure 2

a, DNA strand-displacement implementation of weight activation followed by weight multiplication. Arrows with black-filled and white-filled arrowheads indicate the forwards and backwards directions of a reversible reaction step, respectively. White-filled arrowheads are omitted if a reaction is considered to be approximately irreversible. b,c, Fluorescence kinetics experiments of the activatable weight gate with varying activator (b) and input (c) concentrations. A reporter molecule shown in Extended Data Fig. 4a reacts with the output of this reaction, resulting in an increased fluorescence signal, which is then normalized to concentration based on control experiments. Experimental data (dotted trajectories) are overlaid with mass-action simulations of chemical kinetics obtained by solving ordinary differential equations (solid trajectories). Relative concentrations of the inhibited weight, fuel and reporter are 1.5× , 3× and 2×, respectively. Standard concentration (1×) is 50 nM here and in all other figures. Endpoint measurements of output concentrations are plotted against activator or input concentrations to reveal their relationship. The solid line indicates a linear fit to the experimental data. The dotted line indicates equal input–output concentration, used as a comparison for the experimental data, highlighting the effect of signal amplification. d, Crosstalk evaluation with 18 weight gates and activators. e,f, DNA strand-displacement implementation of supervised learning (e) and label inhibition (f). g,h, Fluorescence kinetics experiments of the learning gate with varying label (g) and input (h) concentrations. The bottom strand in the inhibited activator and the inputs are modified with a fluorophore and a quencher, respectively (Extended Data Fig. 5a). i, Crosstalk evaluation with eight learning gates and input–label pairs. Excess label at 5× was used. The coloured trajectories in d and i indicate output concentrations over 2 h for distinct activators, or activator concentrations over 8 h for distinct input–label pairs, with each colour representing a specific activator or input–label pair.

Source data

Full size image

We characterized the weight gate using fluorescence kinetics experiments (Supplementary Note 1). With fixed input and varying activator concentrations, the output reached the activator level within 2 h, demonstrating accurate 1-bit information transfer from passive to active memory (Fig. 2b and Extended Data Fig. 4d). With fixed activator and varying input concentrations, the output exceeded the input by over 4-fold in 20 h, saturating at the activator level—showing robust weight multiplication and signal amplification (Fig. 2c and Extended Data Fig. 4d).

We assessed weight-activation specificity using crosstalk experiments involving 18 inhibited weights and activators (Fig. 2d and Extended Data Fig. 4f). All matching pairs (diagonal) yielded ≥88% of the target signal, whereas mismatched pairs (306 off-diagonal cases) produced ≤20%, with 287 cases below 10%—indicating excellent specificity. These experiments were performed without competition—each tube contained one weight and one activator. In the actual memory transfer, all weights and activators are present together, and mismatches must compete with matches. We expect real-scenario crosstalk to be at least an order of magnitude better.

The second motif is an activatable transformation gate (Extended Data Fig. 3). Using this motif, we developed a learning gate that stoichiometrically produces an activator signal (Fig. 2e). A key requirement is irreversible consumption of input and label strands to prevent errors in future learning events. A simple allosteric toehold design is reversible, and although a drain molecule could enforce irreversibility, it introduces complications (‘Alternative learning gate design’ in Methods). Instead, we embed irreversibility into the learning gate itself (Fig. 2e). A Tj bulge loop in the Xi domain slows reverse branch migration, and upon top-strand release, the Tj domain forms a hairpin with Tj*, further inhibiting the reverse reaction. We experimentally confirmed irreversibility (Supplementary Fig. 20 and Supplementary Note 5.2) and optimized Xi length to balance strand quality and intermediate-state stability. This minimizes spurious activation during interaction with weight gates (Supplementary Fig. 21 and Supplementary Note 5.3).

Although learning is irreversible when both label and input are present, the label alone must interact reversibly with the learning gate. Otherwise, all gates in a memory would be locked on by one training pattern and respond incorrectly to patterns in the other class. This reversibility is built into a transient intermediate activator (Fig. 2e), which is less stable than the activated weight (Fig. 2a). Consequently, the produced activator followed the expected linear dependence on label and input concentrations, but slightly below ideal values (Fig. 2g,h). To improve kinetics and reaction completion (Extended Data Fig. 5d), we used excess label and added an inhibitor to remove leftover label between training events (Fig. 2f).

We evaluated the learning motif’s specificity using crosstalk experiments with eight learning gates and input–label pairs (Fig. 2i and Extended Data Fig. 5e). Unlike the weight motif, which uses a standard fluorescence reporter, these experiments required distinct fluorophore–quencher strands for each reaction (Extended Data Fig. 5a), limiting the experiment scale owing to cost. All matching pairs produced ≥94% of the target signal, whereas all 56 mismatched cases yielded ≤10%, demonstrating high specificity. As with weight crosstalk tests, these were done without competition; actual learning scenarios are expected to show even lower crosstalk.

Activatable memories

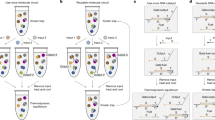
The activatable weight motif enables a DNA neural network to receive memories encoded in activators for performing different tasks. In this section, the activators represent weights from in silico training, allowing us to separately evaluate the function of the programmable processor before integrating it with the memory device. We constructed a network with two 100-bit activatable memories and provided 3 distinct sets of activator strands, each encoding 2 classes of handwritten digits from the Modified National Institute of Standards and Technology (MNIST) database42 (Fig. 3). In previous work, we averaged 100 training patterns per class and selected the top-20 bits to form the weight matrix4. Here, lacking a molecular mechanism for bit selection, classification accuracy declines (Supplementary Fig. 31a). To compensate, we developed a ‘good teacher’ strategy: rank and filter above-average training patterns, then randomly select ten per class (Supplementary Note 5.12)—used here for setting activator concentrations and for training in the next section.

Fig. 3: Pattern classification with activatable memories.
figure 3

a–c, Test patterns selected based on their positions in the weighted sum space for three distinct pairs of MNIST handwritten digits: 0 and 1 (a), 3 and 4 (b), and 6 and 7 (c). Weights are determined as the average of ten training patterns per class. The entire test dataset is shown in light grey. Test patterns within a 20% margin to the diagonal line (s1 = s2) are excluded for experimental feasibility. d,e, Fluorescence kinetics experiments with 12 test patterns per class on activated memories of 0 and 1 in memory 1 and 2 (d), respectively, or swapped in memory 2 and 1 (e). The difference between two output concentrations (Y1 − Y2) at the end of the experiments is shown for all test patterns sorted according to their distance to the diagonal line in the weighted sum space. For the left set of patterns, the distance decreases from left to right; for the right set of patterns, the distance increases. f–i, Endpoint data for testing activated memories of 3 and 4 in memory 1 and 2 (f), respectively, or swapped in memory 2 and 1 (g) or 6 and 7 in memory 1 and 2 (h), respectively, or swapped in memory 2 and 1 (i).

Source data

Full size image

Test patterns were selected based on their positions in the weighted sum space, reflecting classification difficulty. For each class, 12 representative tests were chosen via k-means clustering (k = 12), selecting 1 example per cluster (Fig. 3a–c). To ensure experimental feasibility, we excluded examples within 20% of the diagonal, retaining 53% of zeros and 83% of ones from the dataset. Outside this margin, the network is expected to classify all test patterns correctly with clear binary outputs. Within the margin, classifications are still possible but less binary. Similarly, the expected lower bounds of classification accuracy—determined by the fraction of test patterns outside the 20% margin—for the full MNIST dataset were 56% for threes, 46% for fours, 56% for sixes and 71% for sevens (Supplementary Fig. 31d). Fluorescence kinetics experiments confirmed correct outputs for all test patterns, showing clear on–off separation (Fig. 3d–i). Separation quality correlated with distance from the diagonal: greater distance yielded larger separations. To assess DNA sequence dependence, we encoded digit pairs with swapped memory molecules. Experimental results showed minor differences, consistent with simulations using reaction rates from the motif characterization (Extended Data Fig. 6).

The ability to receive memories enables the DNA neural network to function as a field-programmable device, performing different classification tasks based on the activators provided. Although it is still following instructions rather than learning, this demonstration is powerful—it can execute any combination of commands from a library of hundreds to classify complex and noisy inputs.

Learned weights

The learning motif enables a DNA neural network to develop memories encoded in activators for later computation. In this section, the activators represent weights learned from in vitro training, allowing us to separately evaluate the function of the adaptive memory device before integrating it with the processor. We constructed a network of learning gates that received 100-bit training data from 2 classes of handwritten digits and monitored the produced activators. A robust learning system should handle arbitrary training patterns in any order. To test this, we used a ‘batch training’ procedure, simultaneously presenting all patterns from the same class—analogous to batch training in machine learning. In molecular terms, mixing pre-prepared patterns yields a training mixture where each input strand’s quantity reflects the combined signal from all patterns. Although this method lacks intra-class order variation, it still tests robustness by presenting the two classes in different orders (Fig. 4a). Training with individual patterns would slow learning owing to lower input concentrations and require label inhibition between patterns of different classes, complicating the experiments.

Fig. 4: Learned weights.
figure 4

a, Abstract training process of learning two classes of 100-bit handwritten digits in two distinct orders. Grey and black wires indicate inhibited and learned weights, respectively. b, Fluorescence kinetics experiments that read out the learned weights. Learning was performed as follows: present all 10 training patterns from one class together with the class label, wait for 24 h, add the label inhibitor, wait for 2 h, and then repeat with the second class. After learning was completed, 100 aliquots of the learned memories were each mixed with a unique pair of activatable weight molecules (\({W}_{i,1}^{* }\) and \({W}_{i,2}^{* }\)), a fuel strand (XFi), all 100 input strands (X1 to X100), and a pair of standard reporters that each converts one of the two possible output signals to fluorescence. The two reporters were modified with fluorophores ATTO590 and ATTO488, respectively, allowing for simultaneous readout in two fluorescence channels. Eight hours of kinetics data are shown in two 10-by-10 arrays. Each position in both arrays corresponds to the same sample. Each array corresponds to one of the two fluorescence channels. c, Measured weight concentrations at 4 h and error statistics for learning handwritten digits 0 and 1 in two distinct orders. d,e, Overlaid training patterns (10 per class), representing target weights, and learned weights (measured weight concentrations at 4 h) for learning handwritten digits 3 and 4 (d) or 6 and 7 (e). f, Distribution of errors from experiments shown in c–e. Ø indicates a blank memory. w1 and w2 indicate the weight matrix for memory 1 and 2, respectively.

Source data

Full size image

We performed fluorescence kinetics experiments to read out learned weights after training with digits 0 and 1 (Fig. 4b). Each plot in the data array shows signal increase for one activated weight in the two 100-bit memories. Visually, the digit shapes emerged, confirming successful learning. Quantitatively, pixels with 0 values in all 10 training patterns showed low signals—0.5 ± 0.3% of the total signal for 1 and 1.1 ± 0.4% for 0—whereas other pixels showed up to 13-fold signal increases over background (see endpoint values in Extended Data Fig. 7).

To investigate background noise, we captured snapshots of the training process at the start, midpoint, and end (Fig. 4c). Before training, background signals in memories 1 and 2 were 0.4 ± 0.4% and 0.7 ± 0.3% of the total signal, respectively (Fig. 4c, left column). Memory 2’s higher background persisted post-training (Fig. 4c, middle and right columns), probably owing to sequence variations and synthesis errors causing spurious weight activation. Still, this noise was minimal compared with earlier versions of the learning and activatable weight motifs (Supplementary Note 4.7).

Introducing the first batch of training patterns with their label led to correct storage in the target memory, whereas the other remained largely unaffected (Fig. 4c), demonstrating strong label specificity. The second batch was similarly stored without disrupting the earlier memory. Learned weights were consistent across two training orders, confirming robust learning regardless of which class was presented first or which memory stored each class.

Further robustness was demonstrated using two additional pairs of distinct training patterns (Fig. 4d,e and Extended Data Fig. 8), showing the system’s ability to learn arbitrary information from two classes of 100-bit patterns. Error analysis revealed that memory 2 consistently had more noise than memory 1, regardless of training patterns (Fig. 4f). In addition, a few bits showed lower-than-expected values across training patterns and in both memories, probably owing to secondary structures in the learning intermediates (‘Errors in learned weights’ in Methods).

The ability to develop memories enables the DNA neural network to learn from examples. As shown, it can store arbitrary patterns within a given complexity, integrating them into two memories in any order. Learning is powered solely by the training patterns and labels. After training, the system reaches thermodynamic equilibrium, stably storing learned weights until testing begins.

Testing after training

The true effectiveness of the DNA neural network’s learning ability lies in its classification performance after connecting the memory device to the processor, where learned information is transferred from activators to weights for downstream computation. This step is the most challenging in building a functional learning system. In earlier designs, we achieved 4-bit learning and 4-bit activatable memories separately but not integrated (Supplementary Note 4). With a revised design, we successfully demonstrated integrated 9-bit learning and testing (Supplementary Fig. 21), but failed to scale to 100-bit (Supplementary Fig. 22 and Supplementary Note 5.4). Investigations revealed that unused molecules—more prevalent in larger systems—were the primary issue. For instance, unused learning gates can cause label occlusion, weakening the production of activator signals. They may also leak with weight gates or test inputs, creating spurious memories. We addressed these challenges through design revisions and fabrication techniques (Supplementary Figs. 23–28 and Supplementary Notes 5.5–5.10). Solutions included adding clamps to suppress toeless strand displacement37,43, adjusting annealing ratios, and using clean-up strands to promote competition between full-length and truncated strands, improving gate purity.

To test the scalability of our final design (Fig. 2), we created training and test patterns of increasing complexity (Fig. 5a). We predicted that the performance depends on the ratio of unused-to-used memory bits—that is, inhibited-to-activated weights post-training. Experiments with increasing memory size and varying fractions of activated bits confirmed this (Fig. 5b–d and Extended Data Fig. 9). Overall, performance declined with increasing complexity. However, as long as the total-to-activated bit ratio remained constant, increasing the number of activated bits had minimal impact (Fig. 5e). Performance worsened as this ratio increased (Fig. 5f). These results validated our hypothesis and highlighted a key trade-off: to learn complex patterns, training inputs must not activate too many bits—for example, there is only 1 binary pattern that can be learned if it has 100 ones. Paradoxically, unused bits become the dominant factor degrading testing performance. Scaling beyond two memories introduces further challenges, such as a quadratic increase in annihilator species and biased winner-take-all competition from imperfect reaction rates4.

Fig. 5: Scalability of pattern classification using learned weights.
figure 5

a, Learned weights (top) and test patterns (bottom) with increasing complexity from 4 bits to 100 bits. In learned weights, grey pixels indicate unused memory bits with no associated molecules. White pixels indicate activatable but not activated memory bits with inhibited activator and inhibited weights that are present throughout training and testing. Coloured pixels indicate memory bits activated by training patterns and their labels. In test patterns, each white and black pixel indicates the absence and presence of an input strand, respectively. n is the total number of activable bits in a memory, b is the number of activated bits in a memory and number of ones in an input, and p is an input’s position (s1, s2) in the weighted sum space. b–d, Fluorescence kinetics experiments for testing after learning with three representative cases: b = 4 and n = 4 (b), b = 12 and n = 36 (c), and b = 20 and n = 100 (d). Fluorescence kinetics data for eight test patterns of two classes are shown in two separate plots. The difference between the 2 outputs at 8 h is shown in the bar chart, next to the learned weights. e,f, Performance analysis based on the complexity of activated bits (e) and total bits (f). Error bars represent standard deviation of eight test patterns for each combination of b and n.

Source data

Full size image

The DNA neural network with learning capabilities is far more complex than the previous one using weights trained in silico4. Our 100-bit, 2-memory network involved over 700 distinct species in a single test tube and more than 1,200 unique strands across learning and testing (Fig. 6b). Depending on the number of training patterns, up to 80% of activators and weights must remain inhibited post-training (Fig. 6c). Despite these challenges, we demonstrated successful classification in 72 representative tests after 3 distinct training processes (Fig. 6d and Extended Data Fig. 10), proving that engineered molecular systems can learn complex information-processing tasks.

Fig. 6: A 100-bit pattern classification using learned weights.
figure 6

a, Abstract testing process. b, Comparing the number of initial species in a DNA neural network without4 and with learning capability. c, Comparing the number of inhibited and activated species before and after training. The total numbers are calculated based on a single training pattern where b = 20. d, Simulations (solid trajectories) and fluorescence kinetics experiments (dotted trajectories) of pattern classification for 18 representative cases after 3 distinct training processes. Weight matrices before and after training were taken from the experiments shown in Fig. 4.

Source data

Full size image

Discussion and conclusion

The DNA neural network developed here autonomously performs pattern classification after learning, processing test patterns composed of the same types of molecule as in training, but in new combinations. This demonstrates independence beyond field-programmable devices that rely on instructors to translate environmental signals. It also shows generality, enabling classification beyond simple lookup of previous examples. The system received training patterns over time and stored them into two distinct memories based on label information, demonstrating integration beyond simple memorization. After training, the memories remained passive and isolated from computation until testing began, providing stability beyond short-term memories. Together, these features bring us closer to realizing the future artificial cell envisioned at the beginning of this paper (Extended Data Fig. 1).

The DNA neural network with learning capabilities is remarkably robust given its complexity. Aside from fluorescence reporters, the entire system was constructed using unpurified strands, yet performance remained uncompromised—indicating strong tolerance to impurity-induced molecular noise. Double-stranded complexes were purified using a one-pot procedure to correct stoichiometry errors (for example, all 100 learning gates per memory in one mixture). The robustness, combined with low cost and simple fabrication, makes the system readily accessible for future applications.

Learning has been proposed to accelerate evolution through the Baldwin effect, which reshapes the fitness landscape44,45. Our work explores how chemical systems can learn from an unknown environment, forming memories from past inputs to process future signals. However, supervised learning requires labelled examples—a ‘teacher’—which is incompatible with early life. The next challenge is enabling unsupervised learning, where systems enhance their capabilities through unguided exposure to a molecular environment. In such a regime, the system constantly learns and refines its classification decisions. Achieving this requires overcoming a major limitation: the use-once nature of current DNA neural networks. Computation consumes stored energy, driving the system towards equilibrium. Once used, outputs cannot be reversed without added energy. Although various approaches to reusable enzyme-free DNA circuits have been explored46,47,48,49,50, none are yet scalable. Advancing sustainable computation will be essential to realizing unsupervised learning in molecular systems.

Truly impressive learning behaviours depend on the complexity of neural networks. Although scaling DNA neural networks to the level of the human brain or advanced artificial intelligence models remains infeasible, there is substantial room for increasing their complexity. A current limitation is the absence of spatial organization, which is essential for efficient information encoding in both biological neural networks and electronic computers51. Phase-separated DNA condensates offer a promising solution52. These micrometre-sized droplets, containing billions of branched DNA monomers, could provide the spatial organization needed to scale up learning DNA neural networks by at least an order of magnitude. Alternatively, reaction–diffusion DNA systems53 offer another spatial paradigm for sophisticated pattern formation and classification behaviours54,55.

The potential of learning molecular systems extends far beyond current demonstrations. DNA-based classifiers have been used in disease diagnostics56,57; with learning, they could enable therapeutics that remember previous encounters with disease biomarkers, improving future responses. DNA circuits can also control soft materials, allowing them to expand or contract in response to stimuli58,59. With learning, these materials could adapt based on past experiences. Our work addresses the long-standing challenge of molecular learning, opening paths for intelligent molecular systems. These advances could endow non-living physical systems with adaptive decision-making abilities, transforming fields from molecular therapeutics to programmable active materials60.

Methods

Learning algorithm

The learning algorithm adds each binary training pattern to memory j if binary label lj = 1 (Fig. 1a,b), resulting in weights that are averaged training patterns for each class. Conceptually, this approach is similar to Hebbian learning30, often summarized by the phrase ‘cells that fire together wire together’. Although classical Hebbian learning is an unsupervised learning rule in recurrent neural networks, it can be generalized to feedforward winner-take-all neural networks61. In our case, weight wi,j representing the wire between input node xi and weighted sum node sj is turned on when training data containing input xi and label lj are simultaneously present (Fig. 1a). The training process is also conceptually similar to the widely used clustering algorithm k-means31, but used in a supervised setting62. In our case, k = 2 clusters correspond to the two memories and the means correspond to the averaged training patterns.

Implementation of learning and testing

As the testing phase directly builds on our previous work of DNA-based winner-take-all neural networks4, we first describe this phase as follows before explaining the learning phase. The weighted sum function is divided into weight multiplication and summation (Fig. 1c,d), owing to an architectural constraint that catalytic reactions in the seesaw motif support fan-out but not fan-in37. Weight multiplication and summation are then translated into a catalytic and stoichiometric reaction, respectively. The fan-out of each input multiplied by weights in two or more memories is implemented using an amplification gate motif, whereas the fan-in of weighted sums from all inputs is implemented using an integration gate motif (Extended Data Fig. 3). The catalytic property of the weight multiplication reaction allows for arbitrary analogue weights, including greater than one. The thresholding reaction (with a threshold species Thi representing thi = 0.5) is not explicitly translated from the mathematical function, but enables the clean-up of noisy input signals. The combination of thresholding and catalysis implements a signal restoration function that converts mildly corrupted inputs (high background or signal decay) to ideal binary signals. The winner-take-all function is implemented using pairwise annihilation (facilitated by annihilator Anhi,j) that enables a competition between any two signals, allowing them to turn each other off, and signal restoration (facilitated by restoration gate RGj and fuel YFj) that amplifies the winner species to an ideal on signal. A reporting reaction (facilitated by reporter Repj) is used to stoichiometrically convert an output signal to fluorescence for readout in experiments.

The training phase cannot be implemented with the previously developed reaction mechanisms in the seesaw motif. The key function here is the summed multiplication of binary input and label signals (Fig. 1b), which could be implemented with Xi + Lj → Wi,j, where the total concentration of Wi,j is accumulated over all training patterns that have the same label. However, a problem is that, unlike the product species for all reactions in the testing phase, Wi,j is not a signal species but a double-stranded gate species. To translate a signal species into a gate species, we developed an activatable amplification gate motif where the presence and absence of an activator signal determines the on and off states of the gate, respectively (Extended Data Fig. 3). Using this motif, we can then separate the training process into two reactions: supervised learning Xi + Lj → Acti,j, where an input and label strand collectively produce an activator, and weight activation \({{\rm{Act}}}_{i,j}+{W}_{i,j}^{* }\to {W}_{i,j}\), where the activator turns on a specific weight gate.

The supervised learning reaction can be implemented with an activatable transformation gate motif (Extended Data Fig. 3), using the label as an activator for a learning gate that is initially off (\({{\rm{Act}}}_{i,j}^{* }\)) but can be turned on to react with an input in a training pattern and produce the weight activator (Acti,j). To focus on the essential concept of learning while simplifying other aspects of the algorithm, the scaling of 1/qj (Fig. 1b) is implicitly achieved by using a lower amount of the input strand per training pattern when more patterns are used. Lastly, similar to the thresholding reaction, although not explicitly needed, a label inhibition reaction (facilitated by inhibitor Inhj) is introduced to clean up excess label between training events, facilitating accurate learning.

Combining the training phase and testing phase (Extended Data Fig. 2c), the resulting DNA neural network has five layers (Fig. 1d). The first two layers each utilize the two types of activatable gate motif discussed above, the output of one is an activator signal (Acti,j) and the other is a regular signal (product Pi,j of weight multiplication). This difference in output format may seem insignificant, but along with other desired properties of the two motifs, it led to many important details within the molecular design that will be discussed in the section on motif characterization.

Compared with the DNA neural network without learning capabilities4, this neural network may seem only mildly more complicated with one additional layer, but the network topology has advanced in a non-trivial fashion. The same set of input signals can participate in both the learning and testing phase, reacting with the activatable gates in both of the first two layers. When all gates are present, the only information that determines which gate the input actually reacts with is whether the gate is on or off. When the label is present, it turns on the learning gate; when the activator produced from learning is present, it turns on the weight gate. Undesired spurious activation within these two types of gate will alter the interpretation of the input, for example, confusing a test pattern as a training pattern. Moreover, the DNA neural network without learning capabilities4 used sparse weight matrices to efficiently perform pattern classification tasks, where zero weights corresponded to eliminated weight and fuel species. Here, to learn to perform arbitrary pattern classification tasks within a given pattern complexity and class number, the neural network must have the ability to turn on every element in the weight matrices, requiring the presence of all species in the first two layers. These conditions put more stringent requirements on the molecular design, which cannot be addressed at the individual molecule level, but all interlinked issues such as leak, occlusion, crosstalk and reaction reversibility must be considered as a whole at the system level. We discuss all of these issues in an earlier design (Supplementary Note 4) and summarize a set of system-level design criteria that is applied to the final design (Supplementary Note 3).

During the training phase, all species within the first layer of the DNA neural network will be present, creating passive memories represented by the activator species. These species store the full learned information in a one-to-one fashion (Acti,j encodes Wi,j) but they do not react with any input signals. Transition from training to testing is enabled by combining all species in the remaining four layers with the resulting learning mixture into a single test tube. The added species represent a processor with blank memories. Once the activators and weight gates are mixed together, information transfers from the passive memories to the activated memories, allowing the processor to perform pattern classification tasks using the learned memories (Extended Data Fig. 2b).

Implementation of arbitrary chemical reaction networks

Although not fully verified by theory, we speculate that the extended seesaw motifs now lead to a general-purpose implementation of arbitrary chemical reaction networks (Supplementary Note 4.3). Like the original seesaw motif36, every species in the additional motifs remains one- or two-stranded.

Alternative activatable weight design

To turn on a weight Wi,j, the activator Acti,j could be implemented with two consecutive toeholds using an allosteric toehold mechanism40 that allows for the control of toehold availability via a short regulator strand (Supplementary Fig. 10a). Toehold Xit* encodes the input bit information i and toehold Tj* encodes the memory class information j. However, there are several problems with this design. First, encoding the bit information in a short toehold lacks sufficient specificity for 100-bit patterns, giving rise to crosstalk in weight activation (Supplementary Fig. 17 and Supplementary Note 4.8). Second, all input strands have distinct toehold sequences and react with the weight gates at different rates, leading to the lack of synchronization in the production of weighted sum signals. This asynchrony creates the possibility that a fraction of one weighted sum signal might arrive before the other and become amplified without being annihilated, resulting in biased classification decisions. Third, the activator strand violates the system-level three-letter code (Supplementary Fig. 9 and Supplementary Note 3.3), allowing it to occlude and be occluded by other signal strands. Lastly, like the activator, the label must have a complementary toehold to the input (Supplementary Fig. 11a). Because all input strands have distinct toeholds, 100 label strands per class would be necessary to activate the learning gates for 100-bit training patterns. This is both wasteful, given that the label only needs to encode the class information but not the bit information, and problematic, allowing for increased spurious interactions that reduce the performance of learning and testing.

Design considerations for the weight gate

We investigated the impact of the bulge size and the possibility of replacing the bulge with a nick (Supplementary Fig. 19 and Supplementary Note 5.1). As expected, experiments suggested that a larger bulge drove weight activation more effectively but also increased undesired leak between the input or fuel and the weight gate. Replacing the bulge with a nick results in shorter strands but more strands per complex, reducing synthesis errors at the cost of increased stoichiometry errors (Supplementary Note 3.1). Experiments suggested that the nick provided a higher reaction completion but also more leak. A key difference in the leak mechanism comparing the bulge and the nick design is that although the forward reaction is always bimolecular, the reverse reaction is either unimolecular or bimolecular depending on the design. At a relatively low concentration (for example, 50 nM in our experiments), unimolecular reactions are faster than bimolecular reactions, and thus leak in the bulge design is both kinetically slow and thermodynamically unfavoured. For similar reasons, the nick design not only showed worse leak but also more crosstalk in weight activation, as well as worse leak between the learning gate and the weight gate. On the basis of these observations, we chose the weight gate design with a 2-nt bulge. In addition, a clamp cj is necessary to mitigate leak between the learning gate and the weight gate, preventing spontaneous activation without training. In this design, the system-level three-letter code is satisfied by using non-star domains (As, Cs and Ts) of Tj and Ai on the activator and a two-letter code (As and Ts only) for the universal toehold U and bulge B.

Alternative learning gate design

The desired irreversibility of learning could be provided by a double-stranded drain molecule that converts an intermediate waste to inert wastes with no open toeholds (Supplementary Fig. 11a). This design may seem straightforward, but we discovered several problems upon experimental investigation. First, all drains must be available for learning but most of them will not be consumed depending on the training patterns. Unreacted drains will severely occlude the weight gates in testing, preventing them from being effectively activated (Supplementary Fig. 14 and Supplementary Note 4.5). Second, shortening the toehold on the drain improves the occlusion but sacrifices the robustness of irreversibility, especially when fluorophore and quencher modifications are used to monitor the learning process (Supplementary Fig. 15 and Supplementary Note 4.6). Lastly, mismatches can be introduced to improve irreversibility, but they lead to substantial leak between the learning gates and weight gates, causing spurious memories without training (Supplementary Fig. 16 and Supplementary Note 4.7).

Errors in learned weights

Interestingly, error analysis identified a few bits (27, 85 and 86) that consistently had lower values than expected across all training patterns and both memories (Fig. 4c and Extended Data Fig. 8). Simulations suggested some signal loss during training (Supplementary Fig. 5) but did not explain why certain bits performed worse. We hypothesized that the issue lay in the DNA sequences of the learning gates associated with these bits—our sequence design criteria did not account for intermediate structures in the learning reaction, such as the intermediate activator in which the label is bound to the gate before the input has reacted (Fig. 2e). To investigate further, we used NUPACK63,64 to analyse the secondary structures of all 100 intermediate activators in each memory (Supplementary Fig. 6c). A well-formed structure should have the toehold U* available for binding to the input strand. However, in problematic structures, the toehold partially binds to the Xib* domain owing to the destabilizing effect of the Tj bulge loop. NUPACK analysis predicted that the intermediate activators for bits 27, 85 and 86 were among the worst malformed structures, supporting our hypothesis. Simulations with adjusted reaction rates based on toehold availability showed better agreement with experimental observations (Supplementary Fig. 6d–f). In future work, more stringent sequence design criteria could be applied to avoid malformation in all intermediate structures.

Lessons for engineering complex molecular systems

Two important lessons that we learned for engineering complex molecular systems are as follows. First, a failure mode of the debugging strategy is to focus on individual challenges. A solution for one problem may give rise to another problem somewhere else in the system. With further cascading, in the worst-case scenario, this debugging strategy may form a deadlock in a cycle. After understanding the failure mode, we arrived at an alternative strategy where all challenges are considered as a whole and solutions are devised to address the entire body of challenges simultaneously (Supplementary Note 4.9). Second, a waste of energy may occur if there is no approach to differentiate fabrication problems from design problems. For example, we discovered severe and uneven sample evaporation in source plates for a liquid handler, resulting in wildly inaccurate concentrations that directly affect the computation of the molecular system. Instead of just relying on a better sample storage method, we established a systematic approach to regularly evaluate the sample quality and reorder new strands whenever needed (Supplementary Note 5.13).