Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Observing differential spin currents by resonant inelastic X-ray scattering

Nature volume 645, pages 900–905 (2025)Cite this article

Subjects

This article has been updated

Abstract

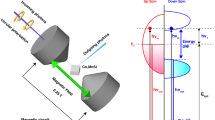
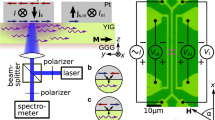
Controlling spin currents, that is, the flow of spin angular momentum, in small magnetic devices, is the principal objective of spin electronics, a main contender for future energy-efficient information technologies1,2. A pure spin current has never been measured directly because the associated electric stray fields and/or shifts in the non-equilibrium spin-dependent distribution functions are too small for conventional experimental detection methods optimized for charge transport3,4. Here we report that resonant inelastic X-ray scattering (RIXS) can bridge this gap by measuring the spin current carried by magnons—the quanta of the spin wave excitations of the magnetic order—in the presence of temperature gradients across a magnetic insulator. This is possible due to the sensitivity of the momentum- and energy-resolved RIXS intensity to minute changes in the magnon distribution under non-equilibrium conditions. We use the Boltzmann equation in the relaxation time approximation to extract transport parameters, such as the magnon lifetime at finite momentum, essential for the realization of magnon spintronics.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Structural, spectroscopic and magnetic properties of YIG at 300 K.
Fig. 2: Spin Seebeck device, SSE voltage and RIXS spectra at 300 K.
Fig. 3: Non-equilibrium RIXS measurement at 80 K.
Fig. 4: Magnon distribution function.

Similar content being viewed by others

Data availability

Data supporting the findings of this study are available upon reasonable request from the corresponding authors.

Change history

  • 17 September 2025

    In the version of the article initially published, the department names in affiliations 4 and 11 were switched and have now been corrected in the HTML and PDF versions of the article. Affiliation 4 now reads “Institute for Materials Research, Tohoku University, Sendai, Japan” and affiliation 11 now reads “WPI Advanced Institute for Materials Research, Tohoku University, Sendai, Japan”.

References

  1. Uchida, K. et al. Observation of the spin Seebeck effect. Nature 455, 778–781 (2008).

    ADS  PubMed  CAS  Google Scholar 

  2. Bauer, G. E., Saitoh, E. & Van Wees, B. J. Spin caloritronics. Nat. Mater. 11, 391–399 (2012).

    ADS  PubMed  CAS  Google Scholar 

  3. Hirsch, J. Overlooked contribution to the Hall effect in ferromagnetic metals. Phys. Rev. B 60, 14787 (1999).

    ADS  CAS  Google Scholar 

  4. Saitoh, E., Ueda, M., Miyajima, H. & Tatara, G. Conversion of spin current into charge current at room temperature: inverse spin-Hall effect. Appl. Phys. Lett. 88, 182509 (2006).

    ADS  Google Scholar 

  5. Han, W., Maekawa, S. & Xie, X.-C. Spin current as a probe of quantum materials. Nat. Mater. 19, 139–152 (2020).

    ADS  PubMed  CAS  Google Scholar 

  6. Gish, J. T., Lebedev, D., Song, T. W., Sangwan, V. K. & Hersam, M. C. Van der Waals opto-spintronics. Nat. Electron. 7, 336–347 (2024).

    CAS  Google Scholar 

  7. Qian, X., Zhou, J. & Chen, G. Phonon-engineered extreme thermal conductivity materials. Nat. Mater. 20, 1188–1202 (2021).

    ADS  PubMed  CAS  Google Scholar 

  8. Franchini, C., Reticcioli, M., Setvin, M. & Diebold, U. Polarons in materials. Nat. Rev. Mater. 6, 560–586 (2021).

    ADS  CAS  Google Scholar 

  9. Choi, Y.-G. et al. Observation of the orbital Hall effect in a light metal Ti. Nature 619, 52–56 (2023).

    ADS  PubMed  CAS  Google Scholar 

  10. Rezende, S. M. Fundamentals of Magnonics Vol. 969 (Springer, 2020).

  11. Dyakonov, M. I. & Perel, V. I. Current-induced spin orientation of electrons in semiconductors. Phys. Lett. A 35, 459–460 (1971).

  12. Pirro, P., Vasyuchka, V. I., Serga, A. A. & Hillebrands, B. Advances in coherent magnonics. Nat. Rev. Mater. 6, 1114–1135 (2021).

    ADS  Google Scholar 

  13. Kukreja, R. et al. X-ray detection of transient magnetic moments induced by a spin current in Cu. Phys. Rev. Lett. 115, 096601 (2015).

    ADS  PubMed  CAS  Google Scholar 

  14. Li, J. et al. Direct detection of pure ac spin current by X-ray pump-probe measurements. Phys. Rev. Lett. 117, 076602 (2016).

    ADS  PubMed  CAS  Google Scholar 

  15. Serga, A. A., Chumak, A. V. & Hillebrands, B. YIG magnonics. J. Phys. D Appl. Phys. 43, 264002 (2010).

    ADS  Google Scholar 

  16. Uchida, K. et al. Longitudinal spin Seebeck effect: from fundamentals to applications. J. Condens. Matter Phys. 26, 343202 (2014).

    CAS  Google Scholar 

  17. Kehlberger, A. et al. Length scale of the spin Seebeck effect. Phys. Rev. Lett. 115, 096602 (2015).

    ADS  PubMed  Google Scholar 

  18. Guo, E.-J. et al. Influence of thickness and interface on the low-temperature enhancement of the spin Seebeck effect in YIG films. Phys. Rev. X 6, 031012 (2016).

    Google Scholar 

  19. Ament, L. J. P., van Veenendaal, M., Devereaux, T. P., Hill, J. P. & van den Brink, J. Resonant inelastic X-ray scattering studies of elementary excitations. Rev. Mod. Phys. 83, 705–767 (2011).

    ADS  CAS  Google Scholar 

  20. Haverkort, M. W. Theory of resonant inelastic X-ray scattering by collective magnetic excitations. Phys. Rev. Lett. 105, 167404 (2010).

    ADS  PubMed  CAS  Google Scholar 

  21. Olsson, K. S. et al. Pure spin current and magnon chemical potential in a nonequilibrium magnetic insulator. Phys. Rev. X 10, 021029 (2020).

    CAS  Google Scholar 

  22. McLaughlin, R., Sun, D., Zhang, C., Groesbeck, M. & Vardeny, Z. V. Optical detection of transverse spin-Seebeck effect in permalloy film using Sagnac interferometer microscopy. Phys. Rev. B 95, 180401 (2017).

    ADS  Google Scholar 

  23. Chumak, A. V., Vasyuchka, V. I., Serga, A. A. & Hillebrands, B. Magnon spintronics. Nat. Phys. 11, 453–461 (2015).

    CAS  Google Scholar 

  24. Pelliciari, J. et al. Tuning spin excitations in magnetic films by confinement. Nat. Mater. 20, 188–193 (2021).

    ADS  PubMed  CAS  Google Scholar 

  25. Gu, Y. et al. Site-specific electronic and magnetic excitations of the skyrmion material Cu2OSeO3. Commun. Phys. 5, 156 (2022).

    CAS  Google Scholar 

  26. Bisogni, V. et al. Femtosecond dynamics of momentum-dependent magnetic excitations from resonant inelastic X-ray scattering in CaCu2O3. Phys. Rev. Lett. 112, 147401 (2014).

    ADS  PubMed  Google Scholar 

  27. Jia, C. et al. Persistent spin excitations in doped antiferromagnets revealed by resonant inelastic light scattering. Nat. Commun. 5, 3314 (2014).

    ADS  PubMed  CAS  Google Scholar 

  28. Robarts, H. C. et al. Dynamical spin susceptibility in La2CuO4 studied by resonant inelastic X-ray scattering. Phys. Rev. B 103, 224427 (2021).

    ADS  CAS  Google Scholar 

  29. Jia, C., Wohlfeld, K., Wang, Y., Moritz, B. & Devereaux, T. P. Using RIXS to uncover elementary charge and spin excitations. Phys. Rev. X 6, 021020 (2016).

    Google Scholar 

  30. Elnaggar, H. et al. Magnetic contrast at spin-flip excitations: an advanced X-ray spectroscopy tool to study magnetic-ordering. ACS Appl. Mater. Interfaces. 11, 36213–36220 (2019).

    PubMed  PubMed Central  CAS  Google Scholar 

  31. Princep, A. J. et al. The full magnon spectrum of yttrium iron garnet. npj Quantum Mater. 2, 63 (2017).

    ADS  Google Scholar 

  32. Li, J. et al. Single- and multimagnon dynamics in antiferromagnetic α − Fe2O3 thin films. Phys. Rev. X 13, 011012 (2023).

    CAS  Google Scholar 

  33. Nambu, Y. et al. Observation of magnon polarization. Phys. Rev. Lett. 125, 027201 (2020).

    ADS  PubMed  CAS  Google Scholar 

  34. Chang, H. et al. Role of damping in spin Seebeck effect in yttrium iron garnet thin films. Sci. Adv. 3, e1601614 (2017).

    ADS  PubMed  PubMed Central  Google Scholar 

  35. Uchida, K. et al. Thermal spin pumping and magnon-phonon-mediated spin-Seebeck effect. J. Appl. Phys. 111, 103903 (2012).

    ADS  Google Scholar 

  36. Jaworski, C. et al. Observation of the spin-Seebeck effect in a ferromagnetic semiconductor. Nat. Mater. 9, 898–903 (2010).

    ADS  PubMed  CAS  Google Scholar 

  37. Kikkawa, T. et al. Critical suppression of spin Seebeck effect by magnetic fields. Phys. Rev. B 92, 064413 (2015).

    ADS  Google Scholar 

  38. Lee, W. et al. Asymmetry of collective excitations in electron- and hole-doped cuprate superconductors. Nat. Phys. 10, 883–889 (2014).

    CAS  Google Scholar 

  39. Dai, P. Antiferromagnetic order and spin dynamics in iron-based superconductors. Rev. Mod. Phys. 87, 855–896 (2015).

    ADS  MathSciNet  CAS  Google Scholar 

  40. Iguchi, R., Uchida, K.-i, Daimon, S. & Saitoh, E. Concomitant enhancement of the longitudinal spin Seebeck effect and the thermal conductivity in a Pt/YIG/Pt system at low temperatures. Phys. Rev. B 95, 174401 (2017).

    ADS  Google Scholar 

  41. Baron, A. Q. R. Recent progress in non-resonant inelastic X-ray scattering. In Proc. 11th International Conference on Inelastic X-Ray Scattering (IEEE, 2019).

  42. Adachi, H. et al. Gigantic enhancement of spin Seebeck effect by phonon drag. Appl. Phys. Lett. 97, 252506 (2010).

    ADS  Google Scholar 

  43. Rezende, S. M. et al. Magnon spin-current theory for the longitudinal spin-Seebeck effect. Phys. Rev. B 89, 014416 (2014).

    ADS  Google Scholar 

  44. Cornelissen, L. J., Peters, K. J. H., Bauer, G. E. W., Duine, R. A. & van Wees, B. J. Magnon spin transport driven by the magnon chemical potential in a magnetic insulator. Phys. Rev. B 94, 014412 (2016).

    ADS  Google Scholar 

  45. Rezende, S. M., Azevedo, A. & Rodríguez-Suárez, R. L. Magnon diffusion theory for the spin Seebeck effect in ferromagnetic and antiferromagnetic insulators. J. Phys. D Appl. Phys. 51, 174004 (2018).

    ADS  Google Scholar 

  46. Boona, S. R. & Heremans, J. P. Magnon thermal mean free path in yttrium iron garnet. Phys. Rev. B 90, 064421 (2014).

    ADS  CAS  Google Scholar 

  47. Jamison, J. S. et al. Long lifetime of thermally excited magnons in bulk yttrium iron garnet. Phys. Rev. B 100, 134402 (2019).

    ADS  CAS  Google Scholar 

  48. Rückriegel, A., Kopietz, P., Bozhko, D. A., Serga, A. A. & Hillebrands, B. Magnetoelastic modes and lifetime of magnons in thin yttrium iron garnet films. Phys. Rev. B 89, 184413 (2014).

    ADS  Google Scholar 

  49. Wei, X.-Y. et al. Giant magnon spin conductivity in ultrathin yttrium iron garnet films. Nat. Mater. 21, 1352–1356 (2022).

    ADS  PubMed  CAS  Google Scholar 

  50. Kubacka, T. et al. Large-amplitude spin dynamics driven by a THz pulse in resonance with an electromagnon. Science 343, 1333–1336 (2014).

    ADS  PubMed  CAS  Google Scholar 

  51. Barker, J. & Bauer, G. E. W. Thermal spin dynamics of yttrium iron garnet. Phys. Rev. Lett. 117, 217201 (2016).

    ADS  PubMed  Google Scholar 

  52. Barker, J. & Bauer, G. E. W. Semiquantum thermodynamics of complex ferrimagnets. Phys. Rev. B 100, 140401 (2019).

    ADS  CAS  Google Scholar 

  53. Vasili, H. B. et al. Direct observation of multivalent states and 4f → 3d charge transfer in Ce-doped yttrium iron garnet thin films. Phys. Rev. B 96, 014433 (2017).

    ADS  Google Scholar 

  54. Dvorak, J., Jarrige, I., Bisogni, V., Coburn, S. & Leonhardt, W. Towards 10 meV resolution: the design of an ultrahigh resolution soft X-ray RIXS spectrometer. Rev. Sci. Instrum. 87, 115109 (2016).

    ADS  PubMed  Google Scholar 

  55. Manley, M. E. et al. Intrinsic anharmonic localization in thermoelectric PbSe. Nat. Commun. 10, 1928 (2019).

    ADS  PubMed  PubMed Central  CAS  Google Scholar 

  56. Boschini, F. et al. Dynamic electron correlations with charge order wavelength along all directions in the copper oxide plane. Nat. Commun. 12, 597 (2021).

    ADS  PubMed  PubMed Central  CAS  Google Scholar 

  57. Nambu, Y. & Shamoto, S. Neutron scattering study on yttrium iron garnet for spintronics. J. Phys. Soc. Jpn. 90, 081002 (2021).

    ADS  Google Scholar 

  58. Tomiyasu, K. et al. Coulomb correlations intertwined with spin and orbital excitations in LaCoO3. Phys. Rev. Lett. 119, 196402 (2017).

    ADS  PubMed  CAS  Google Scholar 

  59. Gomez-Perez, J. M., Vélez, S., Hueso, L. E. & Casanova, F. Differences in the magnon diffusion length for electrically and thermally driven magnon currents in Y3Fe5O12. Phys. Rev. B 101, 184420 (2020).

    ADS  CAS  Google Scholar 

  60. Ganzhorn, K. et al. Temperature dependence of the non-local spin Seebeck effect in YIG/Pt nanostructures. AIP Adv. 7, 085102 (2017).

    ADS  Google Scholar 

  61. Prakash, A. et al. Evidence for the role of the magnon energy relaxation length in the spin Seebeck effect. Phys. Rev. B 97, 020408 (2018).

    ADS  CAS  Google Scholar 

  62. Qu, D., Huang, S. Y., Hu, J., Wu, R. & Chien, C. L. Intrinsic spin Seebeck effect in Au/YIG. Phys. Rev. Lett. 110, 067206 (2013).

    ADS  PubMed  CAS  Google Scholar 

  63. Cunha, R. O., Padrón-Hernández, E., Azevedo, A. & Rezende, S. M. Controlling the relaxation of propagating spin waves in yttrium iron garnet/Pt bilayers with thermal gradients. Phys. Rev. B 87, 184401 (2013).

    ADS  Google Scholar 

  64. Shan, J. et al. Influence of yttrium iron garnet thickness and heater opacity on the nonlocal transport of electrically and thermally excited magnons. Phys. Rev. B 94, 174437 (2016).

    ADS  Google Scholar 

  65. Zhang, S. S.-L. & Zhang, S. Magnon mediated electric current drag across a ferromagnetic insulator layer. Phys. Rev. Lett. 109, 096603 (2012).

    ADS  PubMed  Google Scholar 

  66. Zhang, S. S.-L. & Zhang, S. Spin convertance at magnetic interfaces. Phys. Rev. B 86, 214424 (2012).

    ADS  Google Scholar 

  67. Rezende, S. M. & López Ortiz, J. C. Thermal properties of magnons in yttrium iron garnet at elevated magnetic fields. Phys. Rev. B 91, 104416 (2015).

    ADS  Google Scholar 

  68. de Groot, F. M. F., Kuiper, P. & Sawatzky, G. A. Local spin-flip spectral distribution obtained by resonant X-ray Raman scattering. Phys. Rev. B 57, 14584–14587 (1998).

    ADS  Google Scholar 

  69. Adachi, H., Uchida, K.-i, Saitoh, E. & Maekawa, S. Theory of the spin Seebeck effect. Rep. Prog. Phys. 76, 036501 (2013).

    ADS  PubMed  Google Scholar 

  70. Rezende, S. M., Rodríguez-Suárez, R. L., Cunha, R. O., López Ortiz, J. C. & Azevedo, A. Bulk magnon spin current theory for the longitudinal spin Seebeck effect. J. Magn. Magn. Mater. 400, 171–177 (2016).

    ADS  CAS  Google Scholar 

  71. Rezende, S. M., Rodríguez-Suárez, R. L., Lopez Ortiz, J. C. & Azevedo, A. Thermal properties of magnons and the spin Seebeck effect in yttrium iron garnet/normal metal hybrid structures. Phys. Rev. B 89, 134406 (2014).

    ADS  Google Scholar 

  72. Ratkovski, D. R., Balicas, L., Bangura, A., Machado, F. L. A. & Rezende, S. M. Thermal transport in yttrium iron garnet at very high magnetic fields. Phys. Rev. B 101, 174442 (2020).

    ADS  CAS  Google Scholar 

Download references

Acknowledgements

This work was primarily supported by the US Department of Energy (DOE), Office of Science, Early Career Research Program. The SSE setup was co-supported as part of Programmable Quantum Materials, an Energy Frontier Research Center funded by the DOE, Office of Science, Basic Energy Sciences (BES), under award no. DE-SC0019443. This research used beamline 2-ID of the National Synchrotron Light Source II and the Nanofabrication and Electron Microscopy facilities of the Center for Functional Nanomaterials (CFN), which are DOE, Office of Science User Facilities operated for the DOE Office of Science by Brookhaven National Laboratory under contract no. DE-SC0012704. G.E.W.B. was supported by JSPS Kakenhi Grant Nos. JP22H04965 and JP24H02231. T.K. and E.S. were supported by the JST CREST (JPMJCR20C1 and JPMJCR20T2), the Grant-in-Aid for Scientific Research (grant nos. JP19H05600 and JP24K01326) and the Grant-in-Aid for Transformative Research Areas (grant no. JP22H05114) from JSPS KAKENHI, MEXT Initiative to Establish Next-Generation Novel Integrated Circuits Centers (X-NICS) (grant no. JPJ011438), Japan, and the Institute for AI and Beyond of the University of Tokyo. T.K. also acknowledges support from the Reimei Research Program of Japan Atomic Energy Agency. J.B. acknowledges support from a Royal Society University Research Fellowship. Finally, we are grateful to P. Gambardella, J. P. Hill and C. Mazzoli for their discussions and to D. Bacescu for the engineering support with the sample environment.

Author information

Author notes

  1. Yanhong Gu

    Present address: State Key Laboratory of Low Dimensional Quantum Physics, Beijing Tsinghua Institute for Frontier Interdisciplinary Innovation, Beijing, China

Authors and Affiliations

  1. National Synchrotron Light Source II, Brookhaven National Laboratory, Upton, NY, USA

    Yanhong Gu, Jiemin Li, John Sinsheimer, Lukas Lienhard, Jonathan Pelliciari & Valentina Bisogni

  2. Bragg Centre for Materials Research, University of Leeds, Leeds, UK

    Joseph Barker

  3. School of Physics and Astronomy, University of Leeds, Leeds, UK

    Joseph Barker

  4. Institute for Materials Research, Tohoku University, Sendai, Japan

    Joseph Barker & Gerrit E. W. Bauer

  5. Advanced Science Research Center, Japan Atomic Energy Agency, Tokai, Japan

    Takashi Kikkawa

  6. Center for Functional Nanomaterials, Brookhaven National Laboratory, Upton, NY, USA

    Fernando Camino & Kim Kisslinger

  7. Department of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA

    Jackson J. Bauer & Caroline A. Ross

  8. Department of Physics, Columbia University, New York, NY, USA

    Dmitri N. Basov

  9. Department of Applied Physics, The University of Tokyo, Tokyo, Japan

    Eiji Saitoh

  10. Institute for AI and Beyond, The University of Tokyo, Tokyo, Japan

    Eiji Saitoh

  11. WPI Advanced Institute for Materials Research, Tohoku University, Sendai, Japan

    Eiji Saitoh & Gerrit E. W. Bauer

  12. RIKEN Center for Emergent Matter Science (CEMS), Wako, Japan

    Eiji Saitoh

Authors
  1. Yanhong Gu
    View author publications

    Search author on:PubMed Google Scholar

  2. Joseph Barker
    View author publications

    Search author on:PubMed Google Scholar

  3. Jiemin Li
    View author publications

    Search author on:PubMed Google Scholar

  4. Takashi Kikkawa
    View author publications

    Search author on:PubMed Google Scholar

  5. Fernando Camino
    View author publications

    Search author on:PubMed Google Scholar

  6. Kim Kisslinger
    View author publications

    Search author on:PubMed Google Scholar

  7. John Sinsheimer
    View author publications

    Search author on:PubMed Google Scholar

  8. Lukas Lienhard
    View author publications

    Search author on:PubMed Google Scholar

  9. Jackson J. Bauer
    View author publications

    Search author on:PubMed Google Scholar

  10. Caroline A. Ross
    View author publications

    Search author on:PubMed Google Scholar

  11. Dmitri N. Basov
    View author publications

    Search author on:PubMed Google Scholar

  12. Eiji Saitoh
    View author publications

    Search author on:PubMed Google Scholar

  13. Jonathan Pelliciari
    View author publications

    Search author on:PubMed Google Scholar

  14. Gerrit E. W. Bauer
    View author publications

    Search author on:PubMed Google Scholar

  15. Valentina Bisogni
    View author publications

    Search author on:PubMed Google Scholar

Contributions

V.B. conceived the research project. Y.G. and V.B. designed the study, with contributions from G.E.W.B., J.B. and J.P.; J.J.B. checked the magnetization measurement of the YIG single crystal with guidance from C.A.R.; Y.G. fabricated the SSE devices with help from V.B., F.C., K.K., T.K., E.S., D.N.B. and J.S.; Y.G., J.L., J.P. and V.B. carried out the RIXS measurements and performed the first data interpretation. Y.G. analysed the RIXS data with guidance from V.B.; J.B. and G.B. contributed to the data discussion and the linearized Boltzmann model. L.L. performed the finite element analysis of the temperature gradient across the sample; and Y.G. and V.B. wrote the paper with contributions from all authors.

Corresponding authors

Correspondence to Yanhong Gu or Valentina Bisogni.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature thanks Urs Staub, Qisi Wang and the other, anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data figures and tables

Extended Data Fig. 1 Top view of the RIXS scattering geometry.

a, Experimental set-up for momentum transfer q0.2 = [0.2, 0.2, 0.2] r.l.u. The circularly polarized x-rays ki impinge the sample at an angle θin = 90°. The scattering angle 2Θ between incoming beam ki and outgoing beam kf is fixed at 150°. b, As a but for momentum transfer q−0.2 = [−0.2, −0.2, −0.2] r.l.u., with θin = 60° and 2Θ = 150°.

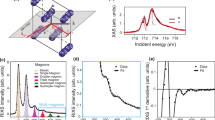
Extended Data Fig. 2 RIXS measurements as a function of temperature on a reference sample.

a, RIXS spectra measured for q0.2 with T = 80 K (blue scattered line) and T = 107 K (light blue scattered line) from the reference sample. b, The intensity difference ΔI between the spectra shown in the panel a drops into the noise level.

Extended Data Fig. 3 RIXS spectra at different sample locations.

a, Sketch of the device, in which the color bar indicates temperature differences, similar to Fig. 2a in the main text. b, Magnon accumulation/depletion as a function of position x calculated for a constant gradient in a symmetric sample. The accumulation/depletion decays on the scale of the magnon relaxation length λ = 2 μm in red and 10 μm in black. c (e), RIXS spectra for q0.2 measured at the hot point (cold point) for two temperature gradients ΔT2 (dark blue) and ΔT4 (light blue). d (f), The RIXS intensity difference between spectra for ΔT2 and ΔT4 and their Gaussian fit (solid line).

Extended Data Fig. 4 Gaussian fitting of the RIXS spectra in the non-equilibrium state.

The data were all acquired at T = 80 K and versus ΔT (ΔT2, ΔT3, and ΔT4), at q0.2= [0.2, 0.2, 0.2] r.l.u. a, and at q−0.2 = [−0.2, −0.2, −0.2] r.l.u. b. The triangles refer to the experimental data points and the solid lines are the fit by the model in Fig. 1c. The (gold, blue, light-blue)-shaded areas are the extracted (elastic, acoustic magnon, optical magnon) contributions, respectively.

Extended Data Table 1 Reported magnon relaxation times at the Brillouin zone center
Full size table

Supplementary information

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gu, Y., Barker, J., Li, J. et al. Observing differential spin currents by resonant inelastic X-ray scattering. Nature 645, 900–905 (2025). https://doi.org/10.1038/s41586-025-09488-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41586-025-09488-9

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing