Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Low-overhead transversal fault tolerance for universal quantum computation

Nature volume 646, pages 303–308 (2025)Cite this article

Subjects

Abstract

Fast, reliable logical operations are essential for realizing useful quantum computers1,2,3. By redundantly encoding logical qubits into many physical qubits and using syndrome measurements to detect and correct errors, we can achieve low logical error rates. However, for many practical quantum error correction codes such as the surface code, owing to syndrome measurement errors, standard constructions require multiple extraction rounds—of the order of the code distance d—for fault-tolerant computation, particularly considering fault-tolerant state preparation4,5,6,7,8,9,10,11,12. Here we show that logical operations can be performed fault-tolerantly with only a constant number of extraction rounds for a broad class of quantum error correction codes, including the surface code with magic state inputs and feedforward, to achieve ‘transversal algorithmic fault tolerance’. Through the combination of transversal operations7 and new strategies for correlated decoding13, despite only having access to partial syndrome information, we prove that the deviation from the ideal logical measurement distribution can be made exponentially small in the distance, even if the instantaneous quantum state cannot be made close to a logical codeword because of measurement errors. We supplement this proof with circuit-level simulations in a range of relevant settings, demonstrating the fault tolerance and competitive performance of our approach. Our work sheds new light on the theory of quantum fault tolerance and has the potential to reduce the space–time cost of practical fault-tolerant quantum computation by over an order of magnitude.

Access through your institution
Buy or subscribe

This is a preview of subscription content, access via your institution

Access options

Access through your institution

Buy this article

  • Purchase on SpringerLink
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Transversal algorithmic fault tolerance.
Fig. 2: Illustration of fault tolerance strategy.
Fig. 3: Numerical verification of fault tolerance.
Fig. 4: The \(| \overline{{\boldsymbol{S}}}\rangle \) state distillation factory.

Similar content being viewed by others

Data availability

The data that support the findings of this study are available at Zenodo103 (https://doi.org/10.5281/zenodo.16552626).

References

  1. Dalzell, A. M. et al. Quantum Algorithms: A Survey of Applications and End-to-End Complexities (Cambridge Univ. Press, 2025).

  2. Beverland, M. E. et al. Assessing requirements to scale to practical quantum advantage. Preprint at https://arxiv.org/abs/2211.07629 (2022).

  3. Babbush, R. et al. Focus beyond quadratic speedups for error-corrected quantum advantage. PRX Quantum 2, 010103 (2021).

    Article  Google Scholar 

  4. Gottesman, D. An introduction to quantum error correction and fault-tolerant quantum computation. Preprint at https://arxiv.org/abs/0904.2557 (2010).

  5. Gottesman, D. Fault-tolerant quantum computation with constant overhead. Quantum Inf. Comput. 14, 1338–1372 (2013).

    MathSciNet  Google Scholar 

  6. Steane, A. M. Error correcting codes in quantum theory. Phys. Rev. Lett. 77, 793–797 (1996).

    Article  ADS  MathSciNet  CAS  PubMed  Google Scholar 

  7. Shor, P. W. Fault-tolerant quantum computation. In Proc. 37th Conference on Foundations of Computer Science 56–65 (IEEE, 1996).

  8. Bravyi, S. B. & Kitaev, A. Y. D. Quantum codes on a lattice with boundary. Preprint at https://arxiv.org/abs/quant-ph/9811052 (1998).

  9. Dennis, E., Kitaev, A., Landahl, A. & Preskill, J. Topological quantum memory. J. Math. Phys. 43, 4452–4505 (2002).

    Article  ADS  MathSciNet  Google Scholar 

  10. Horsman, C., Fowler, A. G., Devitt, S. & Van Meter, R. Surface code quantum computing by lattice surgery. New J. Phys. 14, 123011 (2012).

    Article  ADS  MathSciNet  Google Scholar 

  11. Litinski, D. A game of surface codes: large-scale quantum computing with lattice surgery. Quantum 3, 128 (2019).

    Article  Google Scholar 

  12. Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012).

    Article  ADS  Google Scholar 

  13. Cain, M. et al. Correlated decoding of logical algorithms with transversal gates. Phys. Rev. Lett. 133, 240602 (2024).

    Article  ADS  MathSciNet  CAS  PubMed  Google Scholar 

  14. Gidney, C. & Ekerå, M. How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits. Quantum 5, 433 (2021).

    Article  Google Scholar 

  15. Hastings, M. B. Topological order at nonzero temperature. Phys. Rev. Lett. 107, 210501 (2011).

    Article  ADS  PubMed  Google Scholar 

  16. Raussendorf, R. Quantum computation via translation-invariant operations on a chain of qubits. Phys. Rev. A 72, 052301 (2005).

    Article  ADS  MathSciNet  Google Scholar 

  17. Cohen, L. Z., Kim, I. H., Bartlett, S. D. & Brown, B. J. Low-overhead fault-tolerant quantum computing using long-range connectivity. Sci. Adv. 8, eabn1717 (2022).

    Article  PubMed  PubMed Central  Google Scholar 

  18. Xu, Q. et al. Constant-overhead fault-tolerant quantum computation with reconfigurable atom arrays. Nat. Phys. 20, 1084–1090 (2024).

    Article  CAS  Google Scholar 

  19. Yamasaki, H. & Koashi, M. Time-efficient constant-space-overhead fault-tolerant quantum computation. Nat. Phys. 20, 247–253 (2024).

    Article  CAS  Google Scholar 

  20. Bravyi, S. et al. High-threshold and low-overhead fault-tolerant quantum memory. Nature 627, 778–782 (2024).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  21. Tremblay, M. A., Delfosse, N. & Beverland, M. E. Constant-overhead quantum error correction with thin planar connectivity. Phys. Rev. Lett. 129, 050504 (2022).

    Article  ADS  MathSciNet  CAS  PubMed  Google Scholar 

  22. Bombín, H. Single-shot fault-tolerant quantum error correction. Phys. Rev. X 5, 031043 (2015).

    Google Scholar 

  23. Campbell, E. T. A theory of single-shot error correction for adversarial noise. Quantum Sci. Technol. 4, 025006 (2019).

    Article  ADS  Google Scholar 

  24. Beverland, M. E., Kubica, A. & Svore, K. M. Cost of universality: a comparative study of the overhead of state distillation and code switching with color codes. PRX Quantum 2, 020341 (2021).

    Article  ADS  Google Scholar 

  25. Delfosse, N. & Paetznick, A. Spacetime codes of Clifford circuits. Preprint at https://arxiv.org/abs/2304.05943 (2023).

  26. Gidney, C. Stim: a fast stabilizer circuit simulator. Quantum 5, 497 (2021).

    Article  Google Scholar 

  27. Gottesman, D. Opportunities and challenges in fault-tolerant quantum computation. Preprint at https://arxiv.org/abs/2210.15844 (2022).

  28. Cai, Z., Siegel, A. & Benjamin, S. Looped pipelines enabling effective 3D qubit lattices in a strictly 2D device. PRX Quantum 4, 020345 (2023).

    Article  ADS  Google Scholar 

  29. Duckering, C., Baker, J. M., Schuster, D. I. & Chong, F. T. Virtualized logical qubits: a 2.5D architecture for error-corrected quantum computing. In Proc. Annual International Symposium on Microarchitecture (MICRO) 173–185 (IEEE, 2020).

  30. Calderbank, A. R. & Shor, P. W. Good quantum error-correcting codes exist. Phys. Rev. A 54, 1098 (1996).

    Article  ADS  CAS  PubMed  Google Scholar 

  31. Bravyi, S. & Kitaev, A. Universal quantum computation with ideal Clifford gates and noisy ancillas. Phys. Rev. A 71, 022316 (2005).

    Article  ADS  MathSciNet  Google Scholar 

  32. Postler, L. et al. Demonstration of fault-tolerant universal quantum gate operations. Nature 605, 675–680 (2022).

    Article  ADS  CAS  PubMed  Google Scholar 

  33. Ryan-Anderson, C. et al. Implementing fault-tolerant entangling gates on the five-qubit code and the color code. Preprint at https://arxiv.org/abs/2208.01863 (2022).

  34. Bluvstein, D. et al. Logical quantum processor based on reconfigurable atom arrays. Nature 626, 58–65 (2024).

    Article  ADS  CAS  PubMed  Google Scholar 

  35. Eastin, B. & Knill, E. Restrictions on transversal encoded quantum gate sets. Phys. Rev. Lett. 102, 110502 (2009).

    Article  ADS  PubMed  Google Scholar 

  36. Jochym-O’Connor, T., Kubica, A. & Yoder, T. J. Disjointness of stabilizer codes and limitations on fault-tolerant logical gates. Phys. Rev. X 8, 021047 (2018).

    Google Scholar 

  37. Li, Y. A magic state’s fidelity can be superior to the operations that created it. New J. Phys. 17, 023037 (2015).

    Article  ADS  Google Scholar 

  38. Haah, J. What is your logical qubit. In Proc. Simons Institute Workshop on Advances in Quantum Coding Theory (Simons Institute for the Theory of Computing, 2024).

  39. Cain, M. et al. Fast correlated decoding of transversal logical algorithms. Preprint at https://arxiv.org/abs/2505.13587 (2025).

  40. Serra-Peralta, M., Shaw, M. H. & Terhal, B. M. Decoding across transversal Clifford gates in the surface code. Preprint at https://arxiv.org/abs/2505.13599 (2025).

  41. Kovalev, A. A. & Pryadko, L. P. Fault tolerance of quantum low-density parity check codes with sublinear distance scaling. Phys. Rev. A 87, 020304 (2013).

    Article  ADS  Google Scholar 

  42. Higgott, O., Bohdanowicz, T. C., Kubica, A., Flammia, S. T. & Campbell, E. T. Improved decoding of circuit noise and fragile boundaries of tailored surface codes. Phys. Rev. X 13, 031007 (2023).

    CAS  Google Scholar 

  43. Gurobi Optimization. Gurobi Optimizer Reference Manual (Gurobi Optimization, 2024).

  44. Kim, I. H. et al. Fault-tolerant resource estimate for quantum chemical simulations: case study on Li-ion battery electrolyte molecules. Phys. Rev. Res. 4, 023019 (2022).

    Article  CAS  Google Scholar 

  45. Fowler, A. G. & Gidney, C. Low overhead quantum computation using lattice surgery. Preprint at https://arxiv.org/abs/1808.06709 (2018).

  46. Turner, M. L., Campbell, E. T., Crawford, O., Gillespie, N. I. & Camps, J. Scalable decoding protocols for fast transversal logic in the surface code. Preprint at https://arxiv.org/abs/2505.23567 (2025).

  47. Fowler, A. G. Minimum weight perfect matching of fault-tolerant topological quantum error correction in average O(1) parallel time. Quantum Inf. Comput.15, 145–158 (2015).

    MathSciNet  Google Scholar 

  48. Duclos-Cianci, G. & Poulin, D. Fast decoders for topological quantum codes. Phys. Rev. Lett. 104, 050504 (2010).

    Article  ADS  PubMed  Google Scholar 

  49. Terhal, B. M. Quantum error correction for quantum memories. Rev. Mod. Phys. 87, 307–346 (2015).

    Article  ADS  MathSciNet  Google Scholar 

  50. Breuckmann, N. P. & Eberhardt, J. N. Quantum low-density parity-check codes. PRX Quantum 2, 040101 (2021).

    Article  ADS  Google Scholar 

  51. Tillich, J. P. & Zemor, G. Quantum LDPC codes with positive rate and minimum distance proportional to the square root of the blocklength. IEEE Trans. Inf. Theory 60, 1193–1202 (2014).

    Article  ADS  MathSciNet  Google Scholar 

  52. Panteleev, P. & Kalachev, G. Asymptotically good quantum and locally testable classical LDPC codes. In Proc. Annual ACM Symposium on Theory of Computing 375–388 (IEEE, 2022).

  53. Fawzi, O., Grospellier, A. & Leverrier, A. Constant overhead quantum fault-tolerance with quantum expander codes. In Proc. 2018 IEEE 59th Annual Symposium on Foundations of Computer Science (FOCS) 743–754 (IEEE, 2018).

  54. Gu, S. et al. Single-shot decoding of good quantum LDPC codes. Commun. Math. Phys. 405, 85 (2024).

    Article  ADS  MathSciNet  Google Scholar 

  55. Bombín, H. Gauge color codes: optimal transversal gates and gauge fixing in topological stabilizer codes. New J. Phys. 17, 083002 (2015).

    Article  ADS  MathSciNet  Google Scholar 

  56. Kubica, A., Yoshida, B. & Pastawski, F. Unfolding the color code. New J. Phys. 17, 083026 (2015).

    Article  ADS  MathSciNet  Google Scholar 

  57. Bombin, H. Transversal gates and error propagation in 3D topological codes. Preprint at https://arxiv.org/abs/1810.09575 (2018).

  58. Aharonov, D. & Ben-Or, M. Fault-tolerant quantum computation with constant error rate. SIAM J. Comput. 38, 1207–1282 (1999).

    Article  MathSciNet  Google Scholar 

  59. Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, 2010).

  60. Pattison, C. A., Krishna, A. & Preskill, J. Hierarchical memories: simulating quantum LDPC codes with local gates. Quantum 9, 1728 (2025).

    Article  Google Scholar 

  61. Bravyi, S., Gosset, D., König, R. & Tomamichel, M. Quantum advantage with noisy shallow circuits. Nat. Phys. 16, 1040–1045 (2020).

    Article  CAS  Google Scholar 

  62. Moussa, J. E. Transversal Clifford gates on folded surface codes. Phys. Rev. A 94, 042316 (2016).

    Article  ADS  Google Scholar 

  63. Breuckmann, N. P. & Burton, S. Fold-transversal Clifford gates for quantum codes. Quantum 8, 1372 (2024).

    Article  Google Scholar 

  64. Quintavalle, A. O., Webster, P. & Vasmer, M. Partitioning qubits in hypergraph product codes to implement logical gates. Quantum 7, 1153 (2023).

    Article  Google Scholar 

  65. Bombín, H. et al. Modular decoding: parallelizable real-time decoding for quantum computers. Preprint at https://arxiv.org/abs/2303.04846 (2023).

  66. Higgott, O. & Breuckmann, N. P. Improved single-shot decoding of higher-dimensional hypergraph-product codes. PRX Quantum 4, 020332 (2023).

    Article  ADS  Google Scholar 

  67. Landahl, A. J., Anderson, J. T. & Rice, P. R. Fault-tolerant quantum computing with color codes. Preprint at https://arxiv.org/abs/1108.5738 (2011).

  68. Bravyi, S. & Cross, A. Doubled color codes. Preprint at https://arxiv.org/abs/1509.03239 (2015).

  69. Bacon, D., Flammia, S. T., Harrow, A. W. & Shi, J. Sparse quantum codes from quantum circuits. In Proc. Forty-Seventh Annual ACM Symposium on Theory of Computing 327–334 (ACM, 2014).

  70. Aliferis, P., Gottesman, D. & Preskill, J. Accuracy threshold for postselected quantum computation. Quantum Inf. Comput. 8, 181–244 (2008).

    MathSciNet  Google Scholar 

  71. Lao, L. & Criger, B. Magic state injection on the rotated surface code. In Proc. 19th ACM International Conference on Computing Frontiers 113–120 (ACM, 2022).

  72. Gidney, C. Cleaner magic states with hook injection. Preprint at https://arxiv.org/abs/2302.12292 (2023).

  73. Vasmer, M. & Browne, D. E. Three-dimensional surface codes: transversal gates and fault-tolerant architectures. Phys. Rev. A 100, 012312 (2019).

    Article  ADS  CAS  Google Scholar 

  74. Brown, B. J. A fault-tolerant non-Clifford gate for the surface code in two dimensions. Sci. Adv. 6, 4929–4951 (2020).

    Article  ADS  Google Scholar 

  75. Zhu, G., Sikander, S., Portnoy, E., Cross, A. W. & Brown, B. J. Non-Clifford and parallelizable fault-tolerant logical gates on constant and almost-constant rate homological quantum LDPC codes via higher symmetries. Preprint at https://arxiv.org/abs/2310.16982 (2023).

  76. Bravyi, S., Smith, G. & Smolin, J. A. Trading classical and quantum computational resources. Phys. Rev. X 6, 021043 (2016).

    Google Scholar 

  77. Yoganathan, M., Jozsa, R. & Strelchuk, S. Quantum advantage of unitary Clifford circuits with magic state inputs. Proc. R. Soc. A Math. Phys. Eng. Sci. 475, 20180427 (2018).

    ADS  MathSciNet  Google Scholar 

  78. Gidney, C. Halving the cost of quantum addition. Quantum 2, 74 (2018).

    Article  Google Scholar 

  79. Cuccaro, S. A., Draper, T. G., Kutin, S. A. & Moulton, D. P. A new quantum ripple-carry addition circuit. Preprint at https://arxiv.org/abs/quant-ph/0410184 (2004).

  80. Babbush, R. et al. Encoding electronic spectra in quantum circuits with linear T complexity. Phys. Rev. X 8, 041015 (2018).

    CAS  Google Scholar 

  81. Fowler, A. G. Time-optimal quantum computation. Preprint at https://arxiv.org/abs/1210.4626 (2012).

  82. Litinski, D. & Nickerson, N. Active volume: an architecture for efficient fault-tolerant quantum computers with limited non-local connections. Preprint at https://arxiv.org/abs/2211.15465 (2022).

  83. Knill, E. Quantum computing with very noisy devices. Nature 434, 39–44 (2004).

    Article  ADS  Google Scholar 

  84. Gidney, C. & Fowler, A. G. Flexible layout of surface code computations using AutoCCZ states. Preprint at https://arxiv.org/abs/1905.08916 (2019).

  85. Bravyi, S. & Haah, J. Magic-state distillation with low overhead. Phys. Rev. A 86, 052329 (2012).

    Article  ADS  Google Scholar 

  86. Kubica, A. & Vasmer, M. Single-shot quantum error correction with the three-dimensional subsystem toric code. Nat. Commun. 13, 6272 (2022).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  87. Acharya, R. et al. Suppressing quantum errors by scaling a surface code logical qubit. Nature 614, 676–681 (2023).

    Article  ADS  Google Scholar 

  88. Wootton, J. R. & Loss, D. High threshold error correction for the surface code. Phys. Rev. Lett. 109, 160503 (2012).

    Article  ADS  PubMed  Google Scholar 

  89. Fowler, A. G. Optimal complexity correction of correlated errors in the surface code. Preprint at https://arxiv.org/abs/1310.0863 (2013).

  90. Delfosse, N., Londe, V. & Beverland, M. E. Toward a union-find decoder for quantum LDPC codes. IEEE Trans. Inf. Theory 68, 3187–3199 (2022).

    Article  ADS  MathSciNet  Google Scholar 

  91. Panteleev, P. & Kalachev, G. Degenerate quantum LDPC codes with good finite length performance. Quantum 5, 585 (2019).

    Article  Google Scholar 

  92. Wu, Y., Zhong, L. & Puri, S. Hypergraph minimum-weight parity factor decoder for QEC. In Proc. 2024 APS March Meeting (American Physical Society, 2024).

  93. Bombín, H. Gauge color codes: optimal transversal gates and gauge fixing in topological stabilizer codes. New J. Phys. 17, 083002 (2013).

    Article  MathSciNet  Google Scholar 

  94. Liyanage, N., Wu, Y., Deters, A. & Zhong, L. Scalable quantum error correction for surface codes using FPGA. In Proc. 31st IEEE International Symposium on Field-Programmable Custom Computing Machine (FCCM) 217 (IEEE, 2023).

  95. Richardson, T. & Urbanke, R. Modern Coding Theory (Cambridge Univ. Press, 2008).

  96. Wu, Y. & Zhong, L. Fusion Blossom: fast MWPM decoders for QEC. In Proc. 2023 IEEE International Conference on Quantum Computing and Engineering (QCE) 928–938 (IEEE, 2023).

  97. Grospellier, A. Constant Time Decoding of Quantum Expander Codes and Application to Fault-Tolerant Quantum Computation. PhD thesis, Sorbonne Univ. (2019).

  98. Tan, X., Zhang, F., Chao, R., Shi, Y. & Chen, J. Scalable surface-code decoders with parallelization in time. PRX Quantum 4, 040344 (2023).

    Article  ADS  Google Scholar 

  99. Skoric, L., Browne, D. E., Barnes, K. M., Gillespie, N. I. & Campbell, E. T. Parallel window decoding enables scalable fault tolerant quantum computation. Nat. Commun. 14, 7040 (2023).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  100. Bluvstein, D. et al. A quantum processor based on coherent transport of entangled atom arrays. Nature 604, 451–456 (2022).

    Article  ADS  CAS  PubMed  PubMed Central  Google Scholar 

  101. Pino, J. M. et al. Demonstration of the trapped-ion quantum CCD computer architecture. Nature 592, 209–213 (2021).

    Article  ADS  CAS  PubMed  Google Scholar 

  102. Bartolucci, S. et al. Switch networks for photonic fusion-based quantum computing. Preprint at https://arxiv.org/abs/2109.13760 (2021).

  103. Zhou, H. et al. Data for “Low-Overhead Transversal Fault Tolerance for Universal Quantum Computation”. Zenodo https://doi.org/10.5281/zenodo.16552626 (2025).

Download references

Acknowledgements

We acknowledge the discussion with G. Baranes, P. Bonilla, E. Campbell, S. Evered, S. Geim, L. Jiang, M. Kalinowski, A. Krishna, S. Li, D. Litinski, T. Manovitz, Y. Wu and Q. Xu. We particularly thank C. Pattison for early discussions and for suggesting the simulation of the \(| \overline{S}\rangle \) state distillation factory, and J. Haah for stimulating discussions and insights. We also thank M. Beverland, K. Brown, U. Vazirani and the reviewers for suggestions on presentation. We acknowledge the financial support from IARPA and the Army Research Office, under the Entangled Logical Qubits program (cooperative agreement no. W911NF-23-2-0219), the DARPA ONISQ program (W911NF2010021), the DARPA IMPAQT program (HR0011-23-3-0012), the DARPA MeasQuIT program (HR0011-24-9-0359), the Center for Ultracold Atoms (a NSF Physics Frontiers Center, PHY-1734011), the National Science Foundation (grant nos. PHY-2012023 and CCF-2313084), the Army Research Office MURI (grant no. W911NF-20-1-0082), DOE/LBNL (grant no. DE-AC02-05CH11231), the Wellcome Leap Quantum for Bio program. M.C. acknowledges support from the Department of Energy Computational Science Graduate Fellowship (award no. DE-SC0020347). D.B. acknowledges support from the NSF Graduate Research Fellowship Program (grant no. DGE1745303) and the Fannie and John Hertz Foundation. This research was developed with funding from the Defense Advanced Research Projects Agency (DARPA). The views, opinions and/or findings expressed are those of the author(s) and should not be interpreted as representing the official views or policies of the Department of Defense or the US government.

Author information

Author notes

  1. These authors contributed equally: Hengyun Zhou, Chen Zhao

Authors and Affiliations

  1. QuEra Computing, Boston, MA, US

    Hengyun Zhou, Chen Zhao, Casey Duckering & Sheng-Tao Wang

  2. Department of Physics, Harvard University, Cambridge, MA, USA

    Hengyun Zhou, Madelyn Cain, Dolev Bluvstein, Nishad Maskara, Hong-Ye Hu & Mikhail D. Lukin

  3. AWS Center for Quantum Computing, Pasadena, CA, USA

    Aleksander Kubica

  4. California Institute of Technology, Pasadena, CA, USA

    Aleksander Kubica

  5. Department of Applied Physics, Yale University, New Haven, CT, USA

    Aleksander Kubica

Authors
  1. Hengyun Zhou
    View author publications

    Search author on:PubMed Google Scholar

  2. Chen Zhao
    View author publications

    Search author on:PubMed Google Scholar

  3. Madelyn Cain
    View author publications

    Search author on:PubMed Google Scholar

  4. Dolev Bluvstein
    View author publications

    Search author on:PubMed Google Scholar

  5. Nishad Maskara
    View author publications

    Search author on:PubMed Google Scholar

  6. Casey Duckering
    View author publications

    Search author on:PubMed Google Scholar

  7. Hong-Ye Hu
    View author publications

    Search author on:PubMed Google Scholar

  8. Sheng-Tao Wang
    View author publications

    Search author on:PubMed Google Scholar

  9. Aleksander Kubica
    View author publications

    Search author on:PubMed Google Scholar

  10. Mikhail D. Lukin
    View author publications

    Search author on:PubMed Google Scholar

Contributions

H.Z. formulated the decoding strategy and developed an initial proof sketch through discussions with C.Z., M.C., D.B., C.D., S.-T.W., A.K. and M.D.L.; C.Z., M.C., H.Z. and H.-Y.H. performed numerical simulations; H.Z., A.K., C.Z., M.C., N.M. and C.D. proved the fault tolerance of the scheme. All authors contributed to the writing of the paper.

Corresponding authors

Correspondence to Hengyun Zhou or Mikhail D. Lukin.

Ethics declarations

Competing interests

M.D.L. is a co-founder and shareholder, and H.Z., C.Z., C.D. and S.-T.W. are employees of QuEra Computing. US patent application PCT/US25/22108 (filed on 28 March 2025 and naming H.Z., M.C., C.Z., D.B., M.D.L. and C.D. as co-inventors) contains technical aspects of this paper.

Peer review

Peer review information

Nature thanks Barbara Terhal and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data figures and tables

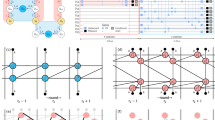
Extended Data Fig. 1 Surface code and transversal operations.

(a) Illustration of the surface code. White circles indicate data qubits. Orange (green) plaquettes are Z (X) stabilizers. The logical \(\overline{Z}\) (\(\overline{X}\)) operator runs vertically (horizontally), and we choose our convention for fixing Z (X) stabilizers to be performing a chain of X (Z) flips to the left (bottom) boundary, as illustrated by the red line. (b) Illustration of transversal \(\overline{H}\) gate, consisting of transversal H gates followed by a reflection along the diagonal. Note that this differs from the usual transversal \(\overline{H}\) gate, which applies a rotation in the second step. For the non-rotated surface code, both choices map X (Z) stabilizers to Z (X) stabilizers and hence are valid, but our choice leads to a smaller transversal partition size for the full circuit. (c) Illustration of transversal \(\overline{S}\) gate, consisting of S and S† gates along the diagonal, together with CZ gates between mirrored qubits.

Extended Data Fig. 2 Illustration of error recovery and frame repair procedures.

We illustrate the procedure for the surface code, where a cross-sectional view with one spatial axis and one time axis is shown. We only illustrate X errors and Z stabilizer measurement errors, which are relevant to interpreting the \(\overline{Z}\) measurement. X errors can terminate on orange boundaries, but cannot terminate on cyan boundaries. The transversal \(\overline{CNOT}\) copies X errors from the top to the bottom, resulting in a branching point (black cross) and an error cluster spanning both code blocks. (a) Error chains and frame flips. Chains of X-type errors (orange lines) lead to syndromes (end points) or terminate on appropriate boundaries. A line segment in the vertical direction is a data qubit X error, while a line segment in the horizontal direction is a measurement error. Note that the X-type error cannot terminate on the transversal Z measurement boundary. The random stabilizer initialization leads to a frame configuration on the logical \(| \,\overline{+}\,\rangle \) initialization, as illustrated by the blue line and the flipped Z stabilizer (blue point). This is similar to the frame stabilizer operator gs illustrated in Extended Data Fig. 1(a). (b) We first infer an error recovery operator, which has the same boundary as the error chain. Together, the error and recovery operator form the fault configuration, which triggers no detectors. We illustrate a few examples (orange lines) that do not lead to a logical error: (1) the fault configuration forms a closed loop and is equivalent to applying a stabilizer; (2) the fault configuration terminates on an initialization boundary; (3) the fault configuration terminates on an out-going, unmeasured logical qubit, but the forward-propagated errors onto the measured logical qubit are equivalent to a stabilizer. A logical error can only happen when the fault configuration spans across two opposing spatial boundaries (red line), which requires an error of weight Θ(d). (c,d) The frame repair operation returns the logical qubit to the code space with all stabilizers +1, corresponding to cancelling any residual flipped stabilizers on the initialization boundary. Note that the error recovery process may also lead to a change that needs to be accounted for by frame repair. An example choice of frame repair is shown in (c), which applies an overall X operator on the logical measurement result. Alternatively, a different choice of frame repair shown in (d), related to the previous one by a frame logical flip, results in identity operation on the logical measurement result.

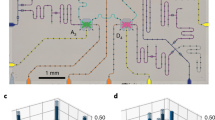
Extended Data Fig. 3 Post-selection rates from the numerical simulation of \(| \overline{{\boldsymbol{S}}}\rangle \) state distillation factory at circuit noise p = 0.1%.

Here the ideal post-selection rates are defined in Eq. (12).

Extended Data Fig. 4 Illustration of a 15-to-1 \(| \overline{{\boldsymbol{T}}}\rangle \) magic state distillation factory, adapted from ref. 24.

The green lines illustrate the application of a logical stabilizer, which allows re-interpretation of measurement results and changes which feed-forwards should be performed.

Supplementary information

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, H., Zhao, C., Cain, M. et al. Low-overhead transversal fault tolerance for universal quantum computation. Nature 646, 303–308 (2025). https://doi.org/10.1038/s41586-025-09543-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/s41586-025-09543-5

Search

Advanced search

Quick links

Nature Briefing AI and Robotics

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: AI and Robotics